【算法】——并查集
作者:指针不指南吗
专栏:算法篇🐾或许会很慢,但是不可以停下🐾
文章目录
- 1.思想
- 2.模板
- 3.应用
- 3.1 合并集合
- 3.2 连通块中点的数量
1.思想
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题(即所谓的并、查)
比如说,我们可以用并查集来判断 某个节点是否属于某棵树等。
-
并查集
-
将两个集合合并
-
询问两个元素是否在一个集合当中
-
-
基本原理
每个集合用一棵树来表示。
树根的编号就是整个集合的编号。
每个节点存储它的父节点,p[x]表示x的父节点。
-
相关问题
-
如何判断树根:
if(p[x]==x) -
如何求x的集合编号:
while(p[x]!=x) x=p[x] -
判断两个元素是否在一个集合里面,即两个元素的编号相同:
find(p[x])==find(p[y]) -
如何合并两个集合:px是x的集合编号,py是y的集合编号。
p[x]=y,即让一个集合 a 的根节点指向另一个集合 b 的根节点,把a直接插在b的根节点下面。
-
-
优化
- 路径压缩:让每个节点都直接指向根节点(祖先)
2.模板
并查集的类型模板这里给出三种,具体题目具体分析,看看需要维护什么,添加什么。
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点// 返回x的祖宗节点
int find(int x)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i; //初始化每个元素的父节点和祖宗节点就是它本身// 合并a和 b所在的两个集合:
p[find(a)] = find(b); //让a的祖宗节点指向b的祖宗节点,a树插在b根节点下面
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量// 返回x的祖宗节点
int find(int x)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{p[i] = i;size[i] = 1; //初始化,每个集合里面只有一个元素
}// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)]; //集合大小相加
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离// 返回x的祖宗节点
int find(int x)
{if (p[x] != x){int u = find(p[x]);d[x] += d[p[x]];p[x] = u;}return p[x];
}// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{p[i] = i;d[i] = 0;
}// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
3.应用
3.1 合并集合
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
M a b或Q a b中的一种。输出格式
对于每个询问指令
Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出Yes,否则输出No。每个结果占一行。
数据范围
1≤n,m≤10510^5105
输入样例:
4 5 M 1 2 M 3 4 Q 1 2 Q 1 3 Q 3 4输出样例:
Yes No Yes
-
代码实现
#include<bits/stdc++.h> using namespace std;const int N=100010;int n,m; //n表示点的数量,m表示操作的次数 int p[N]; //存的每个节点的父节点int find(int x) //返回x的祖宗节点+路径压缩 {if(p[x]!=x) p[x]=find(p[x]);return p[x]; }int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) p[i]=i; //最开始,每个点都各自在一个集合中,so父节点就是他本身;while(m--){char op[2];int a,b;scanf("%s%d %d",op,&a,&b);//合并if(op[0]=='M') p[find(a)]=p[find(b)]; //让a的祖宗节点等于b的祖宗节点,让a的祖宗节点直接插在b祖宗节点下面else{if(find(a)==find(b)) puts("Yes"); //判断是否属于同一个集合else puts("No");} }return 0; }
注意
读入字母M或者是Q的时候,使用字符串op[2],是因为直接用char的话,可能会出现空格换行的问题作物,这种比较保险,记得在后面使用的时候,用op[0],不能直接使用op
puts自动包含换行
3.2 连通块中点的数量
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
C a b,Q1 a b或Q2 a中的一种。输出格式
对于每个询问指令
Q1 a b,如果 a 和 b 在同一个连通块中,则输出Yes,否则输出No。对于每个询问指令
Q2 a,输出一个整数表示点 a 所在连通块中点的数量每个结果占一行。
数据范围
1≤n,m≤10510^5105
输入样例:
5 5 C 1 2 Q1 1 2 Q2 1 C 2 5 Q2 5输出样例:
Yes 2 3
-
思路
-
连通块就是一个点的集合:集合中的点可以相互到达,直接或者是间接都是可以的;
-
这时候我们可以把它类比成一个树,运用并查集,一个点集合,我们可以用一个编号来表示,属于同一个编号,就说明两个点之间可以相互到达,在一个连通块里面;
-
有三个操作:
-
两点之间连一条边,那么这两个点所在集合中的点,都是可以相互到达的,即合成一个连通块,用并查集中的合并操作;
-
判断是否在一个连通块,用并查集的查询;
-
询问一个点集合的数量,需要我们额外维护,初始化的时候每个集合1个,合并的时候,两个集合数量相加,最后输出即可
-
-
-
代码实现
#include<bits/stdc++.h>using namespace std;const int N=1000010; int n,m; int p[N],sizel[N]; //p表示父节点,sizel表示集合的大小,记住sizel里面放的是祖宗节点,后面容易出错int find(int n) //返回祖宗节点 {if(p[n]!=n) p[n]=find(p[n]);return p[n]; }int main() {scanf("%d%d",&n,&m); //读入点的数量和操作的次数for(int i=1;i<=n;i++){ //初始化,父节点就是它本身;集合大小都是1,只有他自己p[i]=i;sizel[i]=1;}char op[5]; while(m--){scanf("%s",op); //读入操作的名字if(op[0]=='C'){ //合并int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) continue; //相同则进入下个循环else{ //不同即操作,两步的顺序不能反!!!sizel[find(b)]+=sizel[find(a)]; //b的集合大小加上a的集合大小p[find(a)]=find(b); //让a的祖宗节点指向b的祖宗节点}}else if(op[1]=='1'){ //查询是否一个集合int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) puts("Yes");else puts("No");}else{if(op[1]=='2') { //输出集合大小int d;scanf("%d",&d);printf("%d\n",sizel[find(d)]); }}}return 0; }

相关文章:

【算法】——并查集
作者:指针不指南吗 专栏:算法篇 🐾或许会很慢,但是不可以停下🐾 文章目录1.思想2.模板3.应用3.1 合并集合3.2 连通块中点的数量1.思想 并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题…...
Python3,为了无损压缩gif动图,我不得不写了一个压缩神器,真香。
gif动图无损压缩1、引言2、代码实战2.1 模块介绍2.2 安装2.3 代码示例3、总结1、引言 小屌丝:鱼哥, 求助~ 求助~ 求助~ 小鱼:你这是告诉我,重要的事情 说三遍吗? 小屌丝:你可以这么理解。 小鱼:…...
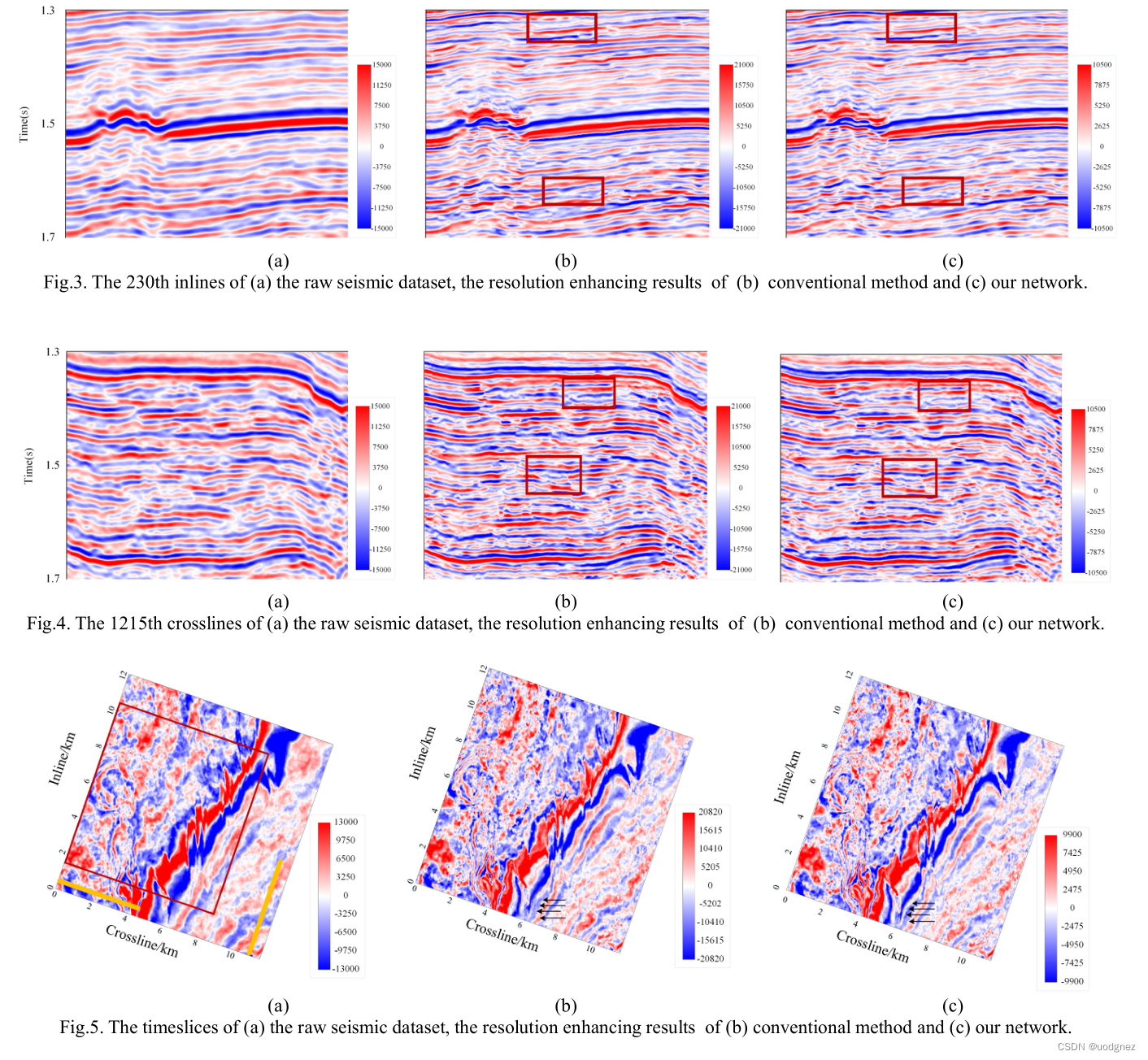
文献阅读 An implementation of the seismic resolution enhancing network based on GAN
题目 An implementation of the seismic resolution enhancing network based on GAN 基于GAN的地震分辨率增强网络的实现 摘要 对于地震数据,本文利用深度学习来学习不同层次的特征并将它们合并以恢复缺失的分辨率。 将GAN网络引入到地震数据处理;对…...

Google员工说出了我不敢说的心里话!
前言:本文来自Beyond的投稿,码农翻身做了修改。今天在Medium上看到一篇文章《The maze is in the mouse》,是一个刚从Google离职的员工写的,揭开了Google内部的各种问题,引发了很多人的共鸣,到目前为止&…...

“御黑行动”进行中,三月重保单位已开放接入!
三月重保在即,对于诸多政企单位来说,正面临着特殊时期的安全保障工作这一重要“大考”。 面对越来越专业且隐匿的攻击,各单位承受着巨大压力,尤其是政府、国企、央企等具有重要地位及广泛社会影响面的单位,其网站及业务…...
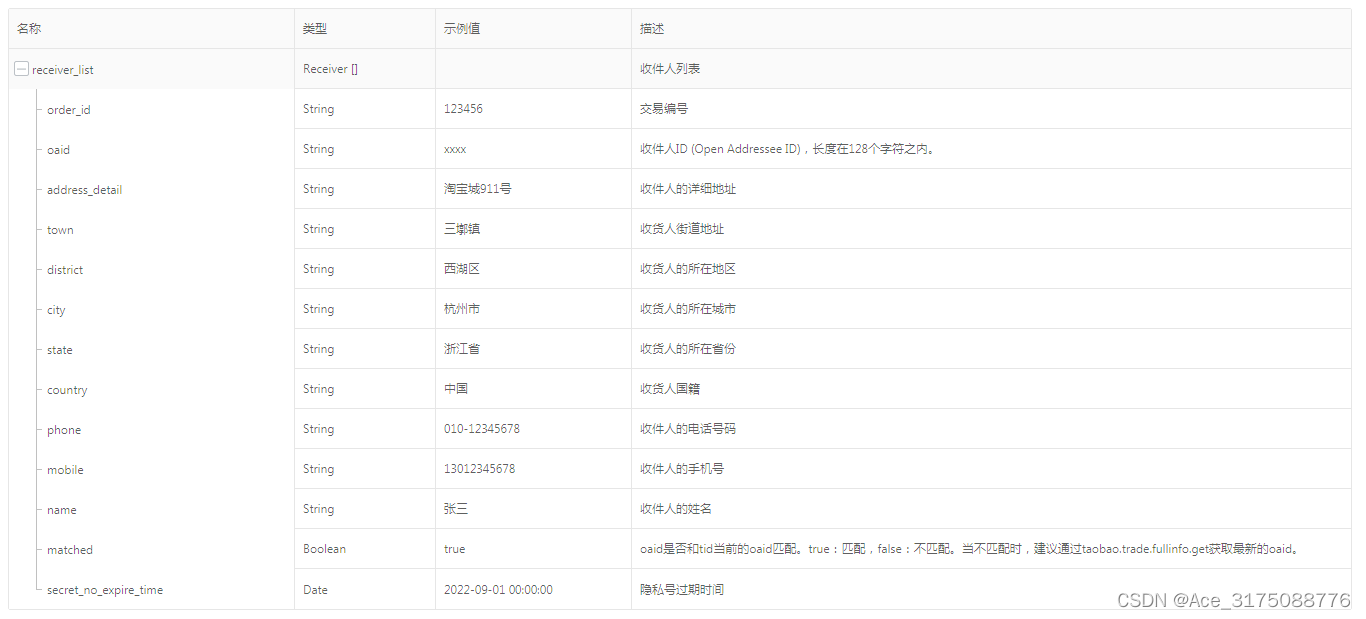
taobao.top.oaid.client.decrypt( 端侧OAID解密 )
¥开放平台免费API不需用户授权 解码OAID(Open Addressee ID),返回收件人信息。该接口用于客户端直接查看订单隐私数据,解密数据不经过ISV服务器,且包含风控等安全检测。 公共参数 请求地址: HTTP地址:http://gw.api.ta…...

QT+OpenGL鼠标操作和模型控制
文章目录QTOpenGL鼠标操作和模型控制鼠标拾取理论有点小复杂从鼠标计算射线第 0 步:2D 视口坐标第 1 步:3d归一化设备坐标第 2 步:4d齐次剪辑坐标第 3 步:4d眼(相机)坐标第 4 步:4d 世界坐标代码展示模型控制多模型加载…...

爱奇艺“资产重定价”:首次全年运营盈利是拐点,底层逻辑大改善
长视频行业历时一年有余的降本增效、去肥增瘦,迎来首个全周期圆满收官的玩家。 北京时间2月22日美股盘前,爱奇艺发布2022年Q4及全年财报,Q4 Non-GAAP净利润明显超越预期,且首次实现全年运营盈利。受业绩提振,爱奇艺盘…...

MySQL —— 库的操作
文章目录1. 创建数据库2. 字符集和校验规则3. 数据库的基本操作3.1 查看数据库3.2 显示创建数据库的语句3.3 修改数据库3.4 删除数据库3.5 备份,还原数据库4. 查看数据库的连接情况1. 创建数据库 基本语法: create database if not exists 数据库名 选项…...

修改shell的命令提示符
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 一、命令提示符格式 从虚拟控制台登陆后,或者从桌面环境的终端进入shell后,就可以看见shell的命令提示符,这意味着可以输入命令了。注意ÿ…...

介绍并比较Apache Hive支持的文件格式
Apache Hive 支持几种熟知的Hadoop使用的文件格式,Hive也能加载并查询其他Hadoop组件创建的不同文件格式,如Pig或MapReduce。本文对比Hive不同文件格式,如:TextFile, SequenceFile, RCFile, AVRO, ORC,Parquet,Clouder…...
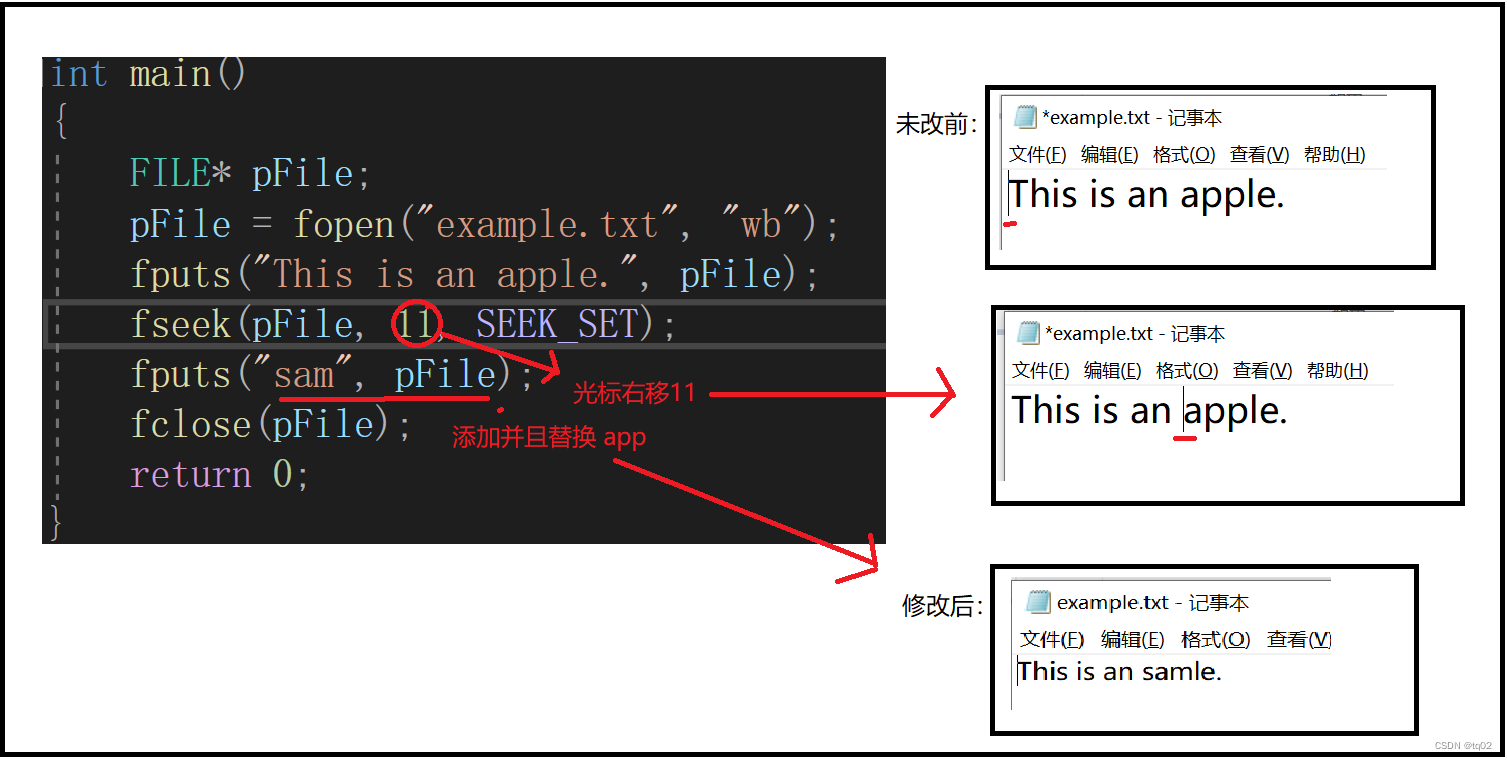
C语言之文件操作
目录 一、什么是文件? 二、C语言如何操作文件 1.操作方式 2.文件指针 2.1 定义文件指针 2.2文件的打开与关闭 2.3文件的顺序读写 2.3文件的随机读写 总结 一、什么是文件? 在电脑磁盘的上的文件。在程序设计中,分为两种:程序…...

Linux->父子进程初识和进程状态
目录 前言: 1. 父子进程创建 2. 进程状态 R(running)状态: S(sleep)状态: D(disk sleep)状态: T(stopped)状态: X(dead)和Z(zombie)状态: 孤儿进程: 前言: 本篇主要讲解关…...

【Linux学习笔记】5.Linux 用户和用户组管理
前言 本章介绍Linux的用户和用户组管理。 Linux 用户和用户组管理 Linux系统是一个多用户多任务的分时操作系统,任何一个要使用系统资源的用户,都必须首先向系统管理员申请一个账号,然后以这个账号的身份进入系统。 用户的账号一方面可以…...

茂名市 2021 年高中信息技术学科素养展评
没事干,发一下去年去比赛的题目。 目录 第一题 30分 第二题 30分 第一题 30分 题目: “姐姐,乘除法运算太难了,有什么办法能熟练掌握吗?”今年 读小学四年级的表弟向李红求救。为了提高表弟的运算能力,…...

【软件测试】测试人不躺平,进军高级自动化测试自救,你的不一样结局......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 随着测试从业年龄的…...
win10环境下安装java开发环境安装java
一:环境介绍 安装系统版本:win10 java版本:java SE 17 二:下载Java安装包 官网下载Java安装包:Java Downloads | Oracle 中国 选择需要的Java版本进行下载,如果没有要选择的版本,可以选择最新…...

【华为OD机试模拟题】用 C++ 实现 - 开心消消乐(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

opencv图像融合
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

没有经验的时候,怎么搞定面试?
在之前的面试技巧,如何写简历上面,我讲了一些方法,希望大家重 视起来。核心其实就一点:他们想要你表现什么能力,以及你在 这个能力之外还有什么。 看清楚这句话的含义,你就可以做到百发百中。具体怎么训练&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
