蓝桥杯---第二讲---二分与前缀和
文章目录
- 前言
- Ⅰ. 数的范围
- 0x00 算法思路
- 0x00 代码书写
- Ⅱ. 数的三次方根
- 0x00 算法思路
- 0x01代码书写
- Ⅲ. 前缀和
- 0x00 算法思路
- 0x01 代码书写
- Ⅳ. 子矩阵的和
- 0x00 算法思路
- 0x01 代码书写
- Ⅴ. 机器人跳跃问题
- 0x00 算法思路
- 0x01 代码书写
- Ⅵ. 四平方和
- 0x00 算法思路
- 0x01 代码书写
- Ⅶ. 分巧克力
- 0x00 算法思路
- 0x01 代码书写
- Ⅷ. 激光炸弹
- 0x00 算法思路
- 0x01 代码书写
- Ⅸ. K倍区间
- 0x00 算法思路
- 0x01 代码书写
- 总结
前言
本篇博客主要打卡记录博主学习蓝桥杯C++AB组辅导课的习题第一章节的题目。
Ⅰ. 数的范围
0x00 算法思路
详细可以看下这一篇博客,详细讲解了二分算法知识
【algorithm】算法基础课—二分查找算法(附笔记 | 建议收藏)
0x00 代码书写
#include <iostream>using namespace std;const int maxn = 100005;
int n, q, x, a[maxn];int main()
{scanf("%d%d", &n, &q);for (int i = 0; i < n; i++) scanf("%d", &a[i]);while (q--) {scanf("%d", &x);int l = 0, r = n - 1;while (l < r) {int mid = l + r >> 1;if (a[mid] < x) l = mid + 1;else r = mid;}if (a[l] != x) {printf("-1 -1\n");continue;}int l1 = l, r1 = n;while (l1 + 1 < r1) {int mid = l1 + r1 >> 1;if (a[mid] <= x) l1 = mid;else r1 = mid;}printf("%d %d\n", l, l1);}return 0;
}
Ⅱ. 数的三次方根
0x00 算法思路
1.迭代的思路,就是无脑迭代100次就可.
2.根据题目法写的方法,其实这个就是while(r-l>谁就行啦).
0x01代码书写
#include<iostream>
#include<cstdio>using namespace std;int main()
{double n;scanf("%lf",&n);double l = -100000, r = 100000;while(r - l > 0.00000001){double mid = (l + r) / 2;if(mid * mid * mid >= n) r = mid;else l = mid;}printf("%.6lf",l);return 0;
}
Ⅲ. 前缀和
0x00 算法思路
详细知识看算法基础课笔记 前缀和与差分
【algorithm】认真讲解前缀和与差分 (图文搭配)
0x01 代码书写
#include<iostream>using namespace std;int n,m;
int sum[100010];int main()
{cin>>n>>m;for(int i=1;i<=n;i++){int tmp;cin>>tmp;sum[i]=sum[i-1]+tmp;}while(m--){int l,r;cin>>l>>r;cout<<sum[r]-sum[l-1]<<endl;}return 0;
}
Ⅳ. 子矩阵的和
0x00 算法思路
详细知识看算法基础课笔记 前缀和与差分
【algorithm】认真讲解前缀和与差分 (图文搭配)
0x01 代码书写
#include<iostream>using namespace std;int n,m,q;
int s[1010][1010];int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>s[i][j];}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];}}while(q--){int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;}return 0;
}
Ⅴ. 机器人跳跃问题
0x00 算法思路
这一道题主要考查了二分答案的算法,通过物理计算得到不论是从低到高,还是从高到低都是:e = 2 * e - h[i] 所以我们假设有一个临界点 E0 满足 0 ~ E0 能量是不满足的,E0 ~ 0x3f3f3f3f 是满足的,就可以使用y总的二分模板了。
0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 100010;int n;
int h[N];bool check(int e)
{for(int i = 1 ; i <= n ; ++ i){e = e * 2 - h[i];if(e >= 1e5) return true;//防止爆intelse if(e < 0) return false; }return true;
}int main()
{cin >> n;for(int i = 1 ; i <= n ; ++ i) cin >> h[i];int l = 0 , r = 1e5;while(l < r){int mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << r << endl;return 0;
}
Ⅵ. 四平方和
0x00 算法思路
这一道题我没学具体的算法思路,感觉不如暴力来的实在,确信哈哈哈
0x01 代码书写
#include<iostream>
#include<cmath>using namespace std;int n;
int a,b,c,d;int main()
{scanf("%d",&n);for(int a=0;a*a<=n;a++){for(int b=a;a*a+b*b<=n;b++){for(int c=b;a*a+b*b+c*c<=n;c++){int t=n-a*a-b*b-c*c;int d=sqrt(t);if(d*d==t){printf("%d %d %d %d\n",a,b,c,d);return 0;}}}}return 0;
}
Ⅶ. 分巧克力
0x00 算法思路
这道题主要考查了二分算法,主要是对于一块大巧克力进行分割,思考的到,当分割的块数越多,边长就越短,块数越少,边长就越大,所以肯定可以有一个临界点 mid 可以使得刚好的块数 满足要求 刚好 >= k 块 如果边长 在 Left ~ mid 之间的话 就是边长很大 所以check函数可以判断这个, 如果在 mid ~ Right 之间的话 肯定是都满足要求的。 最后套用y总的算法模板即可
0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 100010;int n,k;
int h[N],w[N];bool check(int mid)
{int res = 0;for(int i = 0 ; i < n ; ++ i){res += (long long)h[i] / mid * (w[i] / mid);if(res >= k) return true;}return false;
}int main()
{cin >> n >> k;for(int i = 0 ; i < n ; ++ i) cin >> h[i] >> w[i];int l = 1 , r = 1e5;while(l < r){int mid = l + r + 1 >> 1;if(check(mid)) l = mid;else r = mid - 1;}cout << r << endl;return 0;
}
Ⅷ. 激光炸弹
0x00 算法思路
贴一个acwing的图片 : 链接 : AcWing 99. 激光炸弹第一题解


0x01 代码书写
#include<bits/stdc++.h>using namespace std;const int N = 5010;
int cnt,r;
int s[N][N];
int n,m;int main()
{cin >> cnt >> r;r=min(r,5001);n = m = r;while(cnt --){int x,y,w;cin >> x >> y >> w;x ++;y ++;n = max(x,n);m = max(y,m);s[x][y] += w;}for(int i = 1; i <= n; ++ i)for(int j = 1; j <= m ;++ j)// 构造二维前缀和s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];int res = 0; for(int i = r; i <= n ;++ i){for(int j = r; j <= m ;++ j)//根据二维前缀和进行答案计算{res = max(res, s[i][j]-s[i-r][j]-s[i][j-r]+s[i-r][j-r]);}}cout << res << '\n';return 0;
}
Ⅸ. K倍区间
0x00 算法思路
这一道题我只是用了 前缀和做优化,感觉我考试的时候也想不到y总的算法思路,呜呜呜呜呜…
0x01 代码书写
#include<iostream>using namespace std;int n,k;
int a[100010];
int sum[100010];int main()
{cin>>n>>k;for(int i=1;i<=n;i++) cin>>a[i];int ans=0,i=0;for(i=1;i<=n;i++){sum[i]=sum[i-1]+a[i];}for(int j=1;j<=i;j++){for(int s=j+1;s<=i;s++){if((sum[s]-sum[j])%k==0) // 前缀和优化{ans++;}else continue;}}cout<<ans;return 0;
}
总结
本篇博客主要讲解了前缀和 和 二分算法的知识,前面四道题都是算法基础课 的模板题,后面几道题才是真正考查这两个算法的真实难度,开始我也觉得很难很难,但是认真学习完发现其实还是可以学会的,所以请热爱 请认真学习,总会学好,总会获得不小的进步的,加油吧夏目浅石.
相关文章:

蓝桥杯---第二讲---二分与前缀和
文章目录 前言Ⅰ. 数的范围0x00 算法思路0x00 代码书写 Ⅱ. 数的三次方根0x00 算法思路0x01代码书写 Ⅲ. 前缀和0x00 算法思路0x01 代码书写 Ⅳ. 子矩阵的和0x00 算法思路0x01 代码书写 Ⅴ. 机器人跳跃问题0x00 算法思路0x01 代码书写 Ⅵ. 四平方和0x00 算法思路0x01 代码书写 …...
d3dx9_39.dll如何修复?最新修复d3dx9_39.dll方法分享
大家好!今天我要和大家分享的主题是“d3dx9_39.dll丢失的修复方法”。我们都知道,在使用电脑的过程中,经常会遇到各种问题,而其中最常见的就是文件丢失。d3dx9_39.dll就是其中一个常见的丢失文件。那么,如何修复这个丢…...
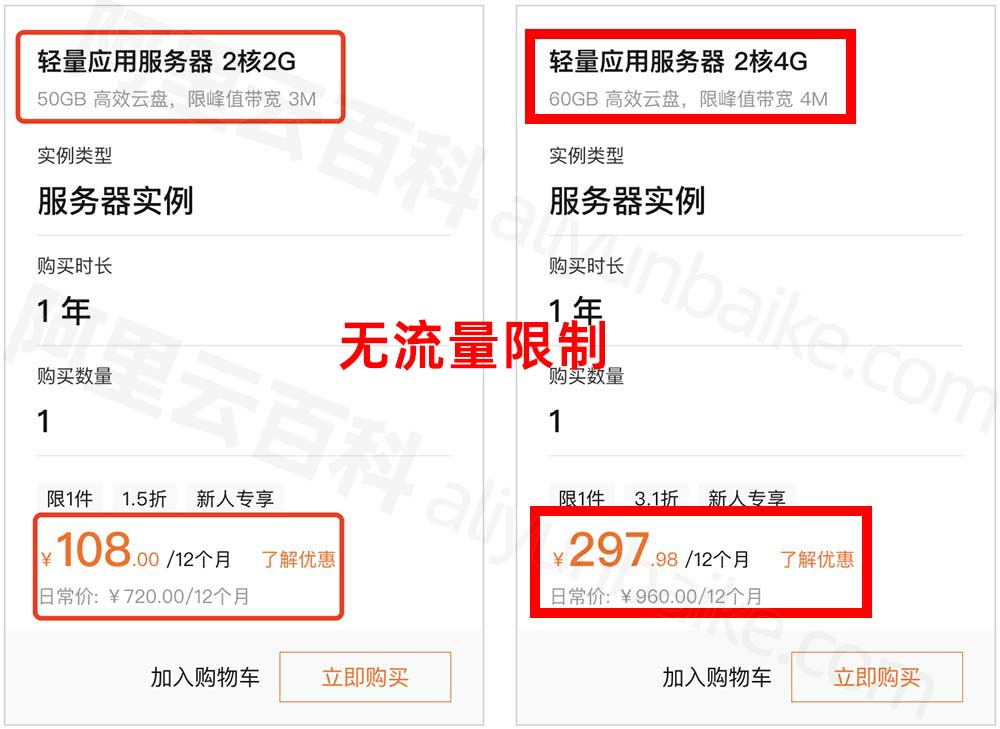
阿里云轻量应用服务器月流量限制说明(部分套餐不限流量)
阿里云轻量应用服务器部分套餐限制月流量,轻量应用服务器按照套餐售卖,有的套餐限制月流量,有的不限制流量。像阿里云轻量2核2G3M带宽轻量服务器一年108元和轻量2核4G4M带宽一年297.98元12个月,这两款是不限制月流量的。阿里云百科…...

项目设计:YOLOv5目标检测+机构光相机(intel d455和d435i)测距
1.介绍 1.1 Intel D455 Intel D455 是一款基于结构光(Structured Light)技术的深度相机。 与ToF相机不同,结构光相机使用另一种方法来获取物体的深度信息。它通过投射可视光谱中的红外结构光图案,然后从被拍摄物体表面反射回来…...

WPF中DataContext的绑定技巧
先看效果: 上面的绑定值都是我们自定义的属性,有了以上的提示,那么我们可以轻松绑定字段,再也不用担心错误了。附带源码。 目录 1.建立mvvm项目 2.cs后台使用DataContext绑定 3.xaml前台使用DataContext绑定 4.xaml前台使用Da…...

【Spring MVC研究】MVC原理:DispatcherServlet的初始化,初始化好等于MVC准备好
文章目录 1. EnableWebMVC 开启 MVC 功能2. 初始化自定义的 MVC 组件2.1. 初始化过程2.2. 如何分析复杂的 Spring 组件注册 3. 容器启动后会初始化 DispatcherServlet4. DispatcherServlet 初始化过程总结5. 资料参考 把DispatcherServlet 准备好意味着服务器已经可以处理请求了…...
Kafka的分布式架构与高可用性
导语 一开始我们就说过Kafka是一款开源的高吞吐、分布式的消息队列系统,那么今天我们就来说下它的分布式架构和高可用性以及双/多中心部署。 Kafka 体系架构简介 以下是 Kafka 的软件架构,整个 Kafka 体系结构由 Producer、Consumer、Broker、ZooKeepe…...

Spring Cloud学习笔记【分布式请求链路跟踪-Sleuth】
文章目录 Spring Cloud Sleuth概述概述主要功能:Sleuth中的术语和相关概念官网 zipkin配置下载运行zipkin下载zipkin运行 demo配置服务提供者 lf-userpom.xmlapplication.ymlUserController 服务调用者 lf-authpom.xmlapplication.ymlAuthController 测试 Spring Cl…...
)
Java开发中的操作日志详解(InsCode AI 创作助手)
Java开发中的操作日志详解 一、操作日志的作用 故障排除和调试: 操作日志可以记录应用程序的各种活动,包括错误、异常、警告和信息性消息。这有助于开发人员快速定位和解决问题。性能分析: 通过记录关键操作和性能指标,操作日志…...

FutureTask和CompletableFuture的模拟使用
模拟了查询耗时操作,并使用FutureTask和CompletableFuture分别获取计算结果,统计执行时长 package org.alllearn.futurtask;import com.google.common.base.Stopwatch; import com.google.common.collect.Lists; import lombok.AllArgsConstructor; imp…...
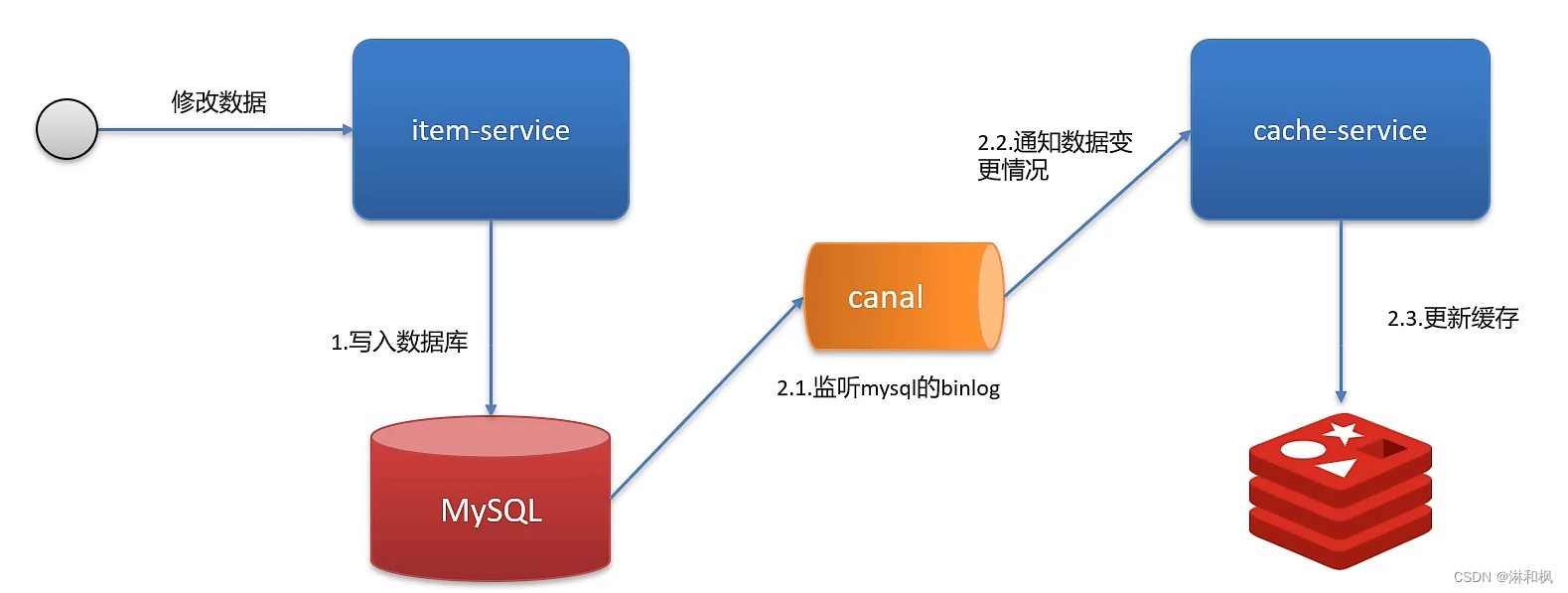
Redis作为缓存,mysql的数据如何与redis进行同步?
Redis作为缓存,mysql的数据如何与redis进行同步? 一定要设置前提,先介绍业务背景 延时双删 双写一致性:当修改了数据库的数据也要同时更新缓存的数据,缓存和数据库的数据要保持一致 读操作:缓存命中,直接返回;缓存未…...

申请免费 SSL 证书为您的小程序加密通信
在今天的网络环境中,数据安全和隐私保护变得尤为重要。无论是网站还是应用程序,为其提供安全的通信渠道都是至关重要的。对于小程序开发者来说,使用 SSL(Secure Sockets Layer)证书可以有效地保障用户数据的安全&#…...
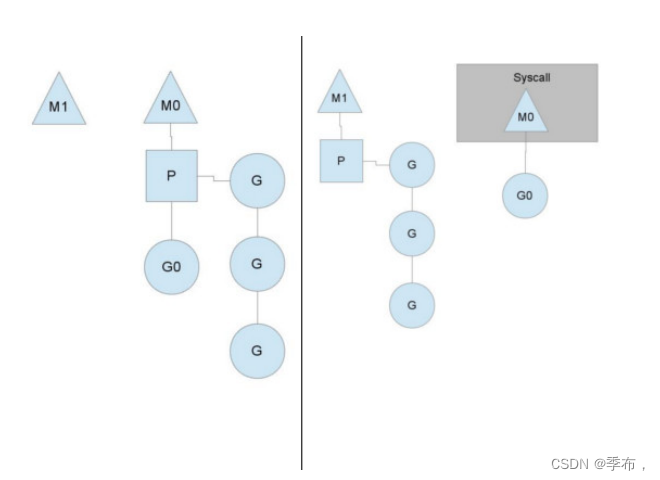
Go 并发编程
并发编程 1.1 并发与并⾏ 并⾏与并发是两个不同的概念,普通解释: 并发:交替做不同事情的能⼒并⾏:同时做不同事情的能⼒ 如果站在程序员的⻆度去解释是这样的: 并发:不同的代码块交替执⾏并⾏…...
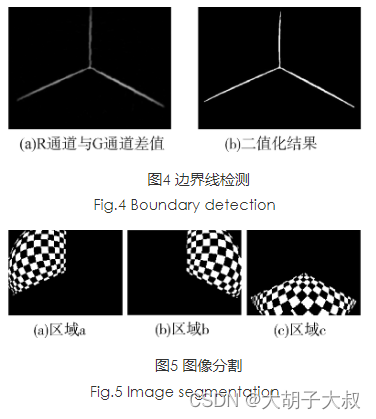
鱼眼相机去畸变(图像拉直/展开/矫正)算法及实战总结
本文介绍两种方法 1、经纬度矫正法 2、棋盘格矫正法 一、经纬度矫正法 1、算法说明 经纬度矫正法, 可以把鱼眼图想象成半个地球, 然后将地球展开成地图,经纬度矫正法主要是利用几何原理, 对图像进行展开矫正。 经过P点的入射光线…...

es6 数据类型
es6 数据类型 map 数据类型 >Map 对象保存键值对。 用途 : Object的key无法支持该数据时需要了解对象大小时 map 数据类型任何值(对象或者原始值) 都可以作为一个键。 Object 的键只能是字符串 let myMap new Map(); let myMap1 new Map(); var keyStrin…...

【postgresql】
看到group by 1,2 和 order by 1, 2。看不懂,google,搜到了Stack Overflow 上有回答 What does SQL clause “GROUP BY 1” mean? 大概意思就是,group by, order by 后面跟数字,指的是 selec…...

【C++】空间配置器 allocator:原理及底层解析
文章目录 空间配置器一级空间配置器二级空间配置器1. 内存池2. SGI-STL中二级空间配置器设计 - - 哈希桶3. 二级空间配置器的空间申请 空间配置器的默认选择空间配置器的在封装:添加了数据类型大小空间配置器对象的构造与析构 容器中的 allocator 空间配置器 提到空…...
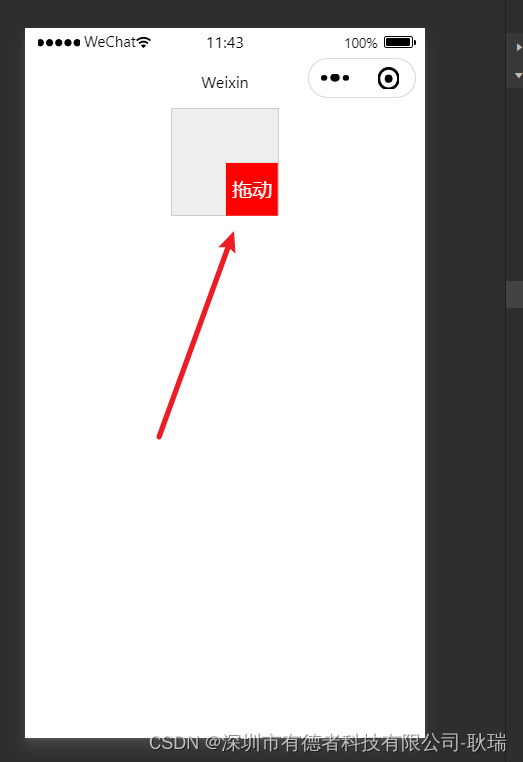
微信小程序 movable-area 区域拖动动态组件演示
movable-area 组件在小程序中的作用是用于创建一个可移动的区域,可以在该区域内拖动视图或内容。这个组件常用于实现可拖动的容器或可滑动的列表等交互效果。 使用 movable-area 组件可以对其内部的 movable-view 组件进行拖动操作,可以通过设置不同的属…...

隔离上网,安全上网
SDC沙盒数据防泄密系统(安全上网,隔离上网) •深信达SDC沙盒数据防泄密系统,是专门针对敏感数据进行防泄密保护的系统,根据隔离上网和安全上网的原则实现数据的代码级保护,不会影响工作效率,不…...

NOSQL Redis 数据持久化 RDB、AOF(二) 恢复
redis 执行flushall 或 flushdb 也会产生dump.rdb文件,但里面是空的。 注意:千万执行,不然rdb文件会被覆盖的。 dump.rdb 文件如何恢复数据 讲备份文件 dump.rdb 移动到redis安装目录并启动服务即可。 dump.rdb 自动触发 和手动触发 自…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
