docker安装Jenkins完整教程
1.docker拉取 Jenkins镜像并启动容器
新版本的Jenkins依赖于JDK11
我们选择docker中jdk11版本的镜像
# 拉取镜像
docker pull jenkins/jenkins:2.346.3-2-lts-jdk11
2.宿主机上创建文件夹
# 创建Jenkins目录文件夹
mkdir -p /data/jenkins_home
# 设置权限
chmod 777 -R /data/jenkins_home
3.启动Jenkins容器
docker run -itd --name jenkins \
-p 8080:8080 \
-p 50000:50000 \
-e JAVA_OPTS="-Dorg.apache.commons.jelly.tags.fmt.timeZone='Asia/Shanghai" \
--privileged=true \
--restart=always \
-v /data/jenkins_home:/var/jenkins_home jenkins/jenkins:2.346.3-2-lts-jdk11
-p 8080是Jenkins默认端口。前面的是宿主机的映射端口
50000是Agent连接Server用到的通信端口。(后面安装JenkinsAgent的时候要注意网络连通性)
-e 时区配置,定义默认的时区。(JAVA_OPTS环境变量为修改时间配置,否则可能jenkins的时间显示有问题!)
-v 持久化数据目录,挂载本地的数据目录。前面的是宿主机的目录后面的是容器内的目录
验证:
docker ps

访问你的 ip:8080 可以看到Jenkins启动成功了

可以通过查看docker日志查看初始化密码
# 查看容器日志
docker logs jenkins
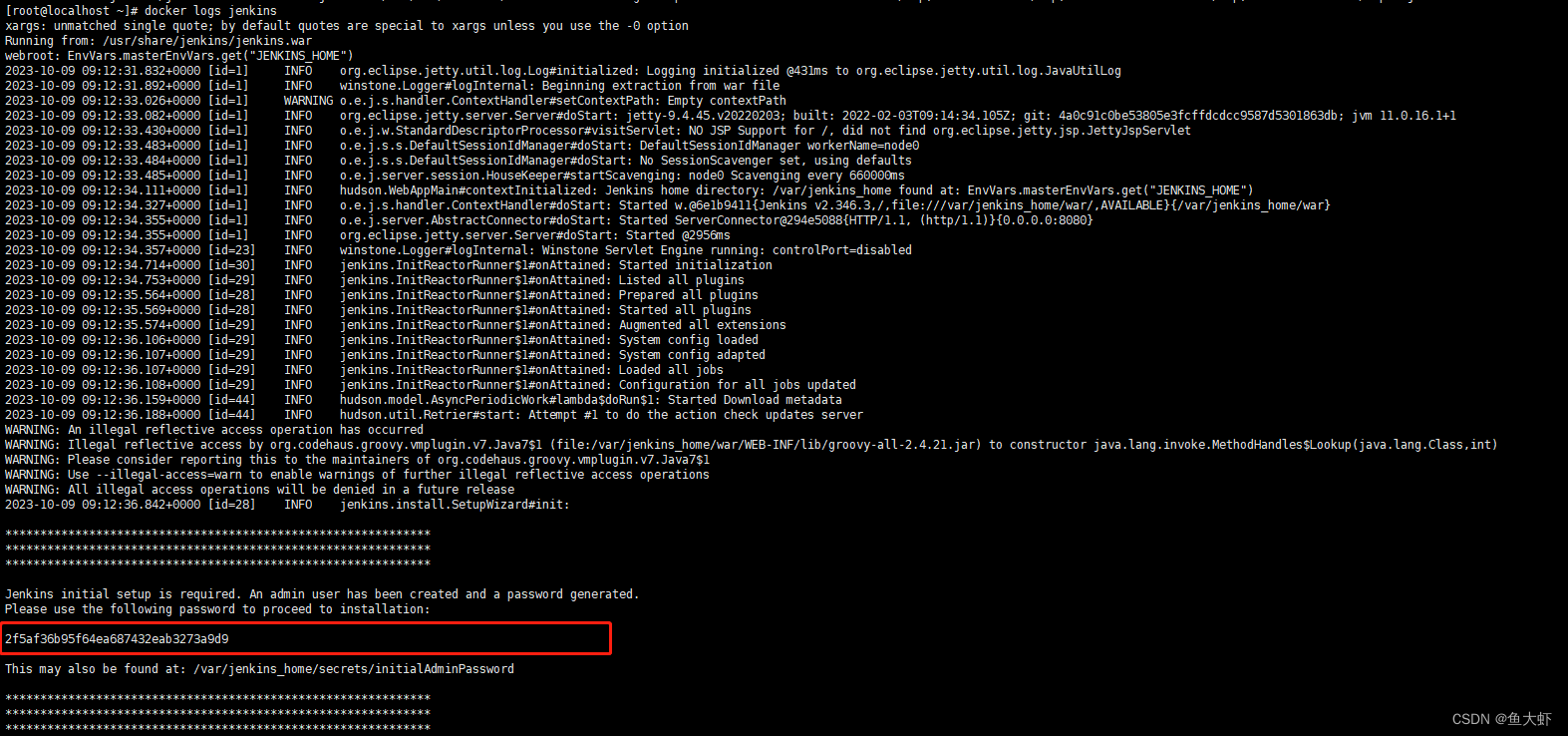
把密码粘贴到上面的框中解锁Jenkins
进入到插件安装页面可自行选择插件或者推荐的安装

安装完插件后进入到设置管理员页面
设置一个管理员账号就可以使用Jenkins了


这样docker安装Jenkins就结束了
相关文章:

docker安装Jenkins完整教程
1.docker拉取 Jenkins镜像并启动容器 新版本的Jenkins依赖于JDK11 我们选择docker中jdk11版本的镜像 # 拉取镜像 docker pull jenkins/jenkins:2.346.3-2-lts-jdk11 2.宿主机上创建文件夹 # 创建Jenkins目录文件夹 mkdir -p /data/jenkins_home # 设置权限 chmod 777 -R /dat…...

[CISCN 2019初赛]Love Math - RCE(异或绕过)
[CISCN 2019初赛]Love Math 1 解题流程1.1 分析1.2 解题题目代码: <?php //听说你很喜欢数学,不知道你是否爱它胜过爱flag if(!isset($_GET[c]))...
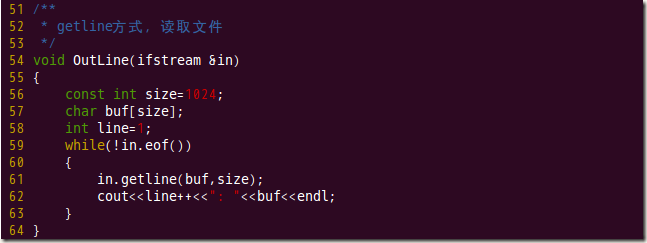
C++ 使用getline()从文件中读取一行字符串
我们知道,getline() 方法定义在 istream 类中,而 fstream 和 ifstream 类继承自 istream 类,因此 fstream 和 ifstream 的类对象可以调用 getline() 成员方法。 当文件流对象调用 getline() 方法时,该方法的功能就变成了从指定文件中读取一行字符串。 该方法有以下 2 种语…...
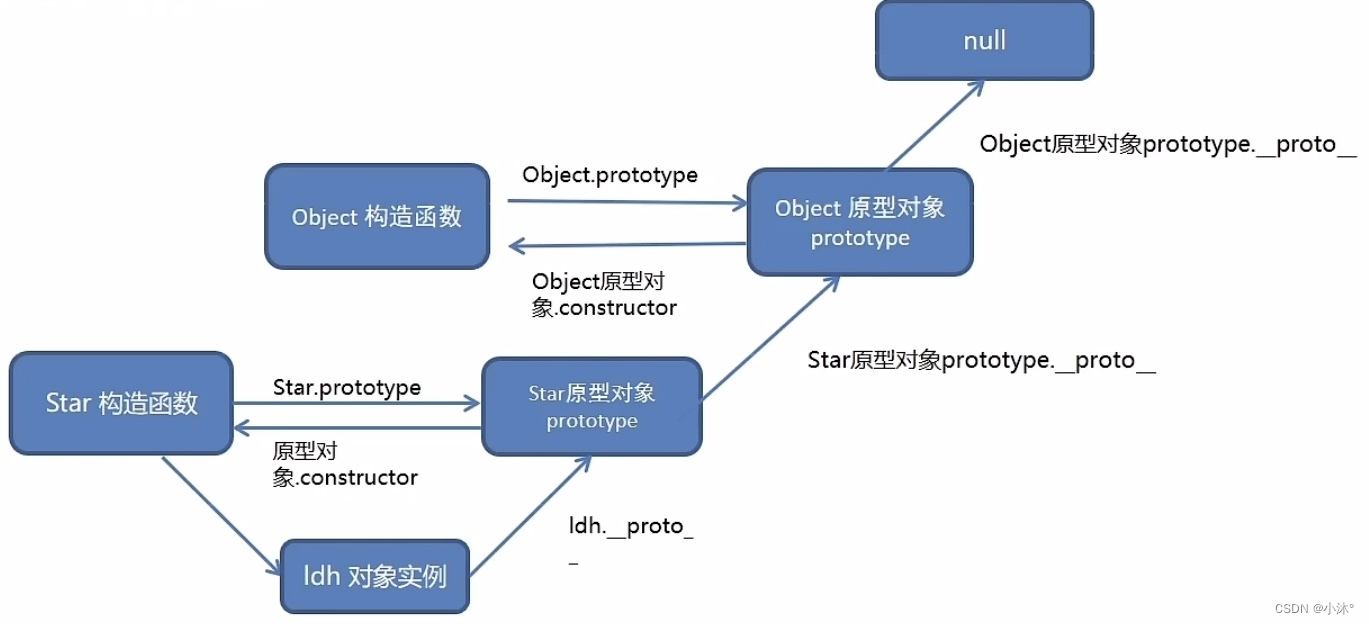
JS进阶-原型
原型 原型就是一个对象,也称为原型对象 构造函数通过原型分配的函数是所有对象所共享的 JavaScript规定,每一个构造函数都有一个prototype属性,指向另一个对象,所以我们也称为原型对象 这个对象可以挂载函数,对象实…...

虹科方案 | 汽车CAN/LIN总线数据采集解决方案
全文导读:现代汽车配备了复杂的电子系统,CAN和LIN总线已成为这些系统之间实现通信的标准协议,为了开发和优化汽车的电子功能,汽车制造商和工程师需要可靠的数据采集解决方案。基于PCAN和PLIN设备,虹科提供了一种高效、…...

HTML5+CSSDAY4综合案例一--热词
样式展示图: 代码如下: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>热词…...
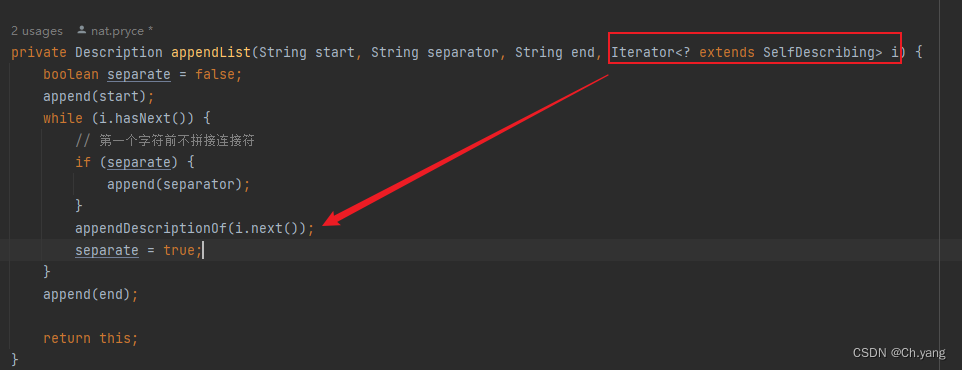
【源码】hamcrest 源码阅读 泛型 extends 和迭代器模式
文章目录 前言1. 泛型参数和自定义迭代器1.1 使用场景1.2 实现 2. 值得一提 前言 官方文档 Hamcrest Tutorial 上篇文章 Hamcrest 源码阅读及空对象模式、模板方法模式的应用 本篇文章 迭代器模式 1. 泛型参数和自定义迭代器 hamcrest 作为一个matcher库,把某个…...
IntelliJ IDEA 2023.1 版本可以安装了
Maven 的导入时间更加快了。 收到的有邮件提醒安装。 安装后的版本,其实就是升级下,并没有什么主要改变。 IntelliJ IDEA 2023.1 版本可以安装了 - 软件技术 - OSSEZMaven 的导入时间更加快了。 收到的有邮件提醒安装。 安装后的版本,其实就是…...

安全论坛和外包平台汇总
文章目录 一. 网络安全论坛汇总二. 外包平台汇总1. 国内:2. 国外 一. 网络安全论坛汇总 安全焦点BugTraq:http://www.fuzzysecurity.com/Exploit-DB:https://www.exploit-db.com/hackone:https://www.hackerone.com/FreeBuf&…...

9-2-Dataset创建-import调用
文章目录 utils_dataset.pymain-调用utils_dateset.pyutils_dataset.py 1默认:没有改变尺寸,数据集中的图像可以是任意形状尺寸。dataloader中必须令batch_size=1 transforms.Resize((宽,高))(image) 和 batch_size=1 必须用其一 原因:当batch_size>1时,每个batch的数…...

XSS原理
原理: 这是一种将任意 Javascript 代码插入到其他Web用户页面里执行以达到攻击目的的漏洞。攻击者利用浏览器的动态展示数据功能,在HTML页面里嵌入恶意代码。当用户浏览改页时,这些潜入在HTML中的恶意代码会被执行,用户浏览器被攻…...
)
记一个带批注、表头样式的导入导出excel方法(基于easyexcel)
技术栈:easyexcel-2.2.10,poi-4.1.2,lombok,hutool-5.8.19;公司自用导入导出方法,可能不是那么的优雅,但胜在稳定实用。 /*** Author 955* Date 2023-10-10 11:52* Description 错误批注信息对…...
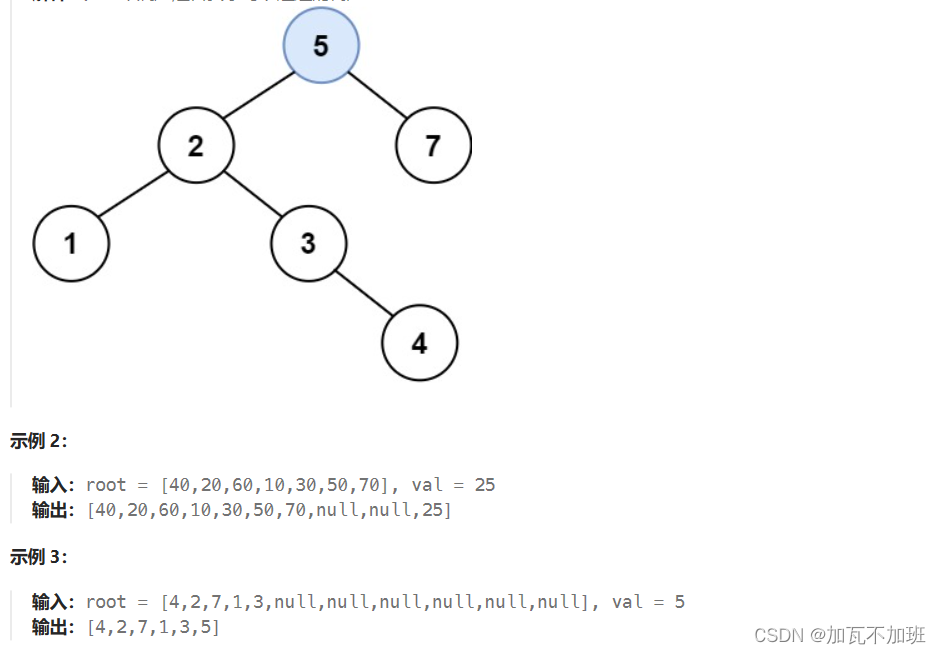
二叉搜索树--新增节点-力扣 701 题
例题细节二叉搜索树的基础操作-CSDN博客也讲过了(put),下面给出递归实现 public TreeNode insertIntoBST(TreeNode node, int val) {//找到空位了if(node null) {return new TreeNode(val);}if(val < node.val) {//一直找到有null的位置…...
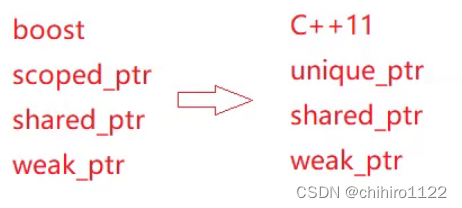
C++ - 智能指针 - auto_ptr - unique_ptr - std::shared_ptr - weak_ptr
前言 C当中的内存管理机制需要我们自己来进行控制,比如 在堆上 new 了一块空间,那么当这块空间不需要再使用的时候。我们需要手动 delete 掉这块空间,我们不可能每一次都会记得,而且在很大的项目程序当中,造成内存泄漏…...
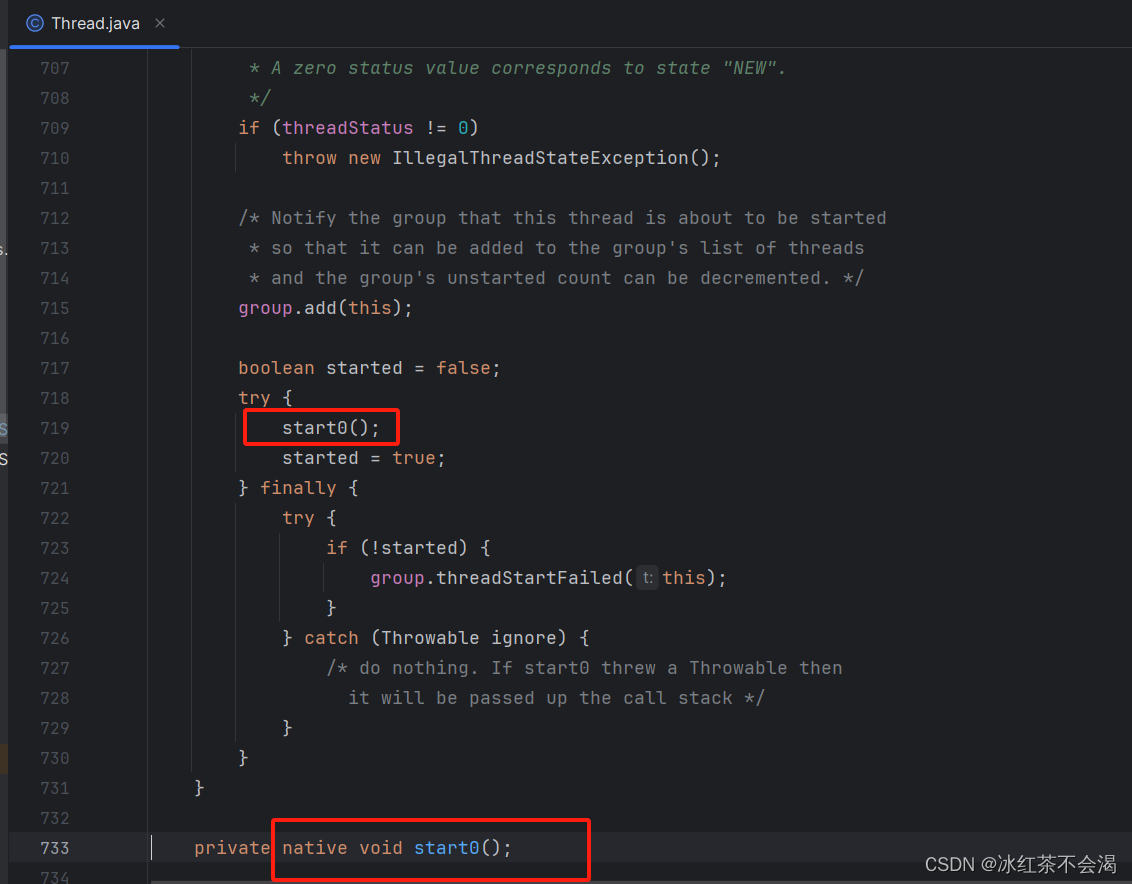
【快速入门】JVM之类加载机制与Native
感慨: 如何定义一个合格的Java程序员,Java程序员要了解掌握哪些知识点,网上的面试题太多了,后端需要了解掌握的知识点太多太多了,Java基础、数据结构、异常、多线程、Spring、Spring boot、事务、算法、数据库…...

R实现数据分布特征的视觉化——多笔数据之间的比较
大家好,我是带我去滑雪! 如果要对两笔数据或者多笔数据的分布情况进行比较,Q-Q图、柱状图、星形图都是非常好的选择,下面开始实战。 (1)绘制Q-Q图 首先导入数据bankwage.csv文件,该数据集…...

TCPUDP
TCP 1.什么是TCP TCP是处于运输层的通信协议,该协议能够实现数据的可靠性传输。 2.TCP报文格式 源端口和目的端口:各占两个字节,发送进程的端口和接收进程的端口号。 序号:占4个字节,序号如果增加到溢出,则下一个序…...
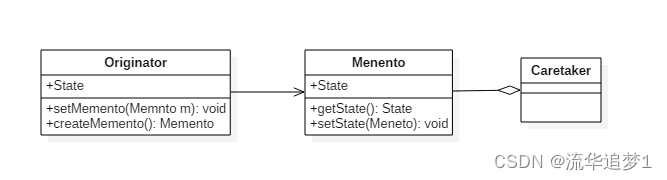
设计模式 - 备忘录模式
目录 一. 前言 二. 实现 三. 优缺点 一. 前言 备忘录模式又称快照模式,是一种行为型设计模式。它可以在不破坏封装性的前提下捕获一个对象的内部状态,并在对象之外保存这个状态,以便在需要的时候恢复到原先保存的状态。在不违反封装的情况…...

OpenCV4(C++)—— 几何图形的绘制
文章目录 一、基本图形1、线2、线圆3、线椭圆4、矩形 二、多边形 一、基本图形 1、线 绘制线,要给出两个点坐标 void cv::line(InputOutputArray img, Point pt1, Point pt2, const Scalar& color, int thickness 1, int lineType LINE_8, int shift 0);…...
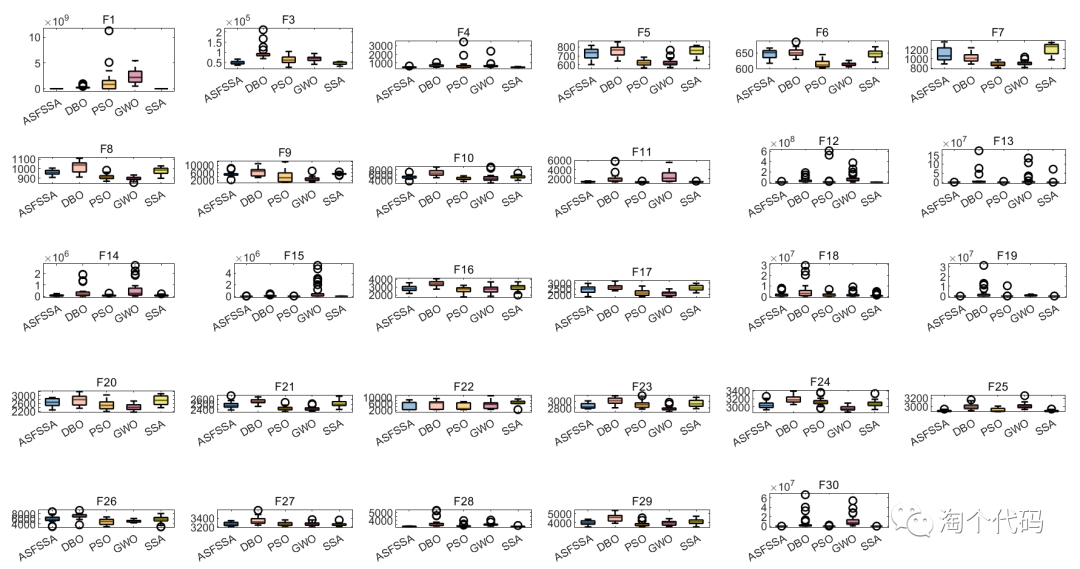
智能优化算法常用指标一键导出为EXCEL,CEC2017函数集最优值,平均值,标准差,最差值,中位数,秩和检验,箱线图...
声明:对于作者的原创代码,禁止转售倒卖,违者必究! 之前出了一篇关于CEC2005函数集的智能算法指标一键统计,然而后台有很多小伙伴在询问其他函数集该怎么调用。今天采用CEC2017函数集为例,进行展示。 为了突…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
