CF1692G 2^Sort 题解
CF1692G 2^Sort 题解
- 题目
- 链接
- 字面描述
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码实现
题目
链接
https://www.luogu.com.cn/problem/CF1692G
字面描述
题面翻译
给你一个长度为 n(∑n<2⋅105)n \ (\sum n < 2\cdot 10^5)n (∑n<2⋅105) 的数组 aaa,问你在这个数组中,有多少个长度为 k+1(1≤k<n)k + 1 \ (1\le k < n)k+1 (1≤k<n) 的区间,符合以下的条件:
20⋅ai<21⋅ai+1<22⋅ai+2<⋯<2k⋅ai+k注:i为这个区间开始的位置2^0 \cdot a_i < 2^1 \cdot a_{i + 1} < 2^2 \cdot a_{i + 2} < \dotsi < 2^k \cdot a_{i + k}\\ \footnotesize{注:i 为这个区间开始的位置} 20⋅ai<21⋅ai+1<22⋅ai+2<⋯<2k⋅ai+k注:i为这个区间开始的位置
由tzyt翻译
题目描述
Given an array $ a $ of length $ n $ and an integer $ k $ , find the number of indices $ 1 \leq i \leq n - k $ such that the subarray $ [a_i, \dots, a_{i+k}] $ with length $ k+1 $ (not with length $ k $ ) has the following property:
- If you multiply the first element by $ 2^0 $ , the second element by $ 2^1 $ , …, and the ( $ k+1 $ )-st element by $ 2^k $ , then this subarray is sorted in strictly increasing order.
More formally, count the number of indices $ 1 \leq i \leq n - k $ such that $ $KaTeX parse error: Can't use function '$' in math mode at position 84: …\cdot a_{i+k}. $̲ $
输入格式
The first line contains an integer $ t $ ( $ 1 \leq t \leq 1000 $ ) — the number of test cases.
The first line of each test case contains two integers $ n $ , $ k $ ( $ 3 \leq n \leq 2 \cdot 10^5 $ , $ 1 \leq k < n $ ) — the length of the array and the number of inequalities.
The second line of each test case contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \leq a_i \leq 10^9 $ ) — the elements of the array.
The sum of $ n $ across all test cases does not exceed $ 2 \cdot 10^5 $ .
输出格式
For each test case, output a single integer — the number of indices satisfying the condition in the statement.
样例 #1
样例输入 #1
6
4 2
20 22 19 84
5 1
9 5 3 2 1
5 2
9 5 3 2 1
7 2
22 12 16 4 3 22 12
7 3
22 12 16 4 3 22 12
9 3
3 9 12 3 9 12 3 9 12
样例输出 #1
2
3
2
3
1
0
提示
In the first test case, both subarrays satisfy the condition:
- $ i=1 $ : the subarray $ [a_1,a_2,a_3] = [20,22,19] $ , and $ 1 \cdot 20 < 2 \cdot 22 < 4 \cdot 19 $ .
- $ i=2 $ : the subarray $ [a_2,a_3,a_4] = [22,19,84] $ , and $ 1 \cdot 22 < 2 \cdot 19 < 4 \cdot 84 $ .
In the second test case, three subarrays satisfy the condition: - $ i=1 $ : the subarray $ [a_1,a_2] = [9,5] $ , and $ 1 \cdot 9 < 2 \cdot 5 $ .
- $ i=2 $ : the subarray $ [a_2,a_3] = [5,3] $ , and $ 1 \cdot 5 < 2 \cdot 3 $ .
- $ i=3 $ : the subarray $ [a_3,a_4] = [3,2] $ , and $ 1 \cdot 3 < 2 \cdot 2 $ .
- $ i=4 $ : the subarray $ [a_4,a_5] = [2,1] $ , but $ 1 \cdot 2 = 2 \cdot 1 $ , so this subarray doesn’t satisfy the condition.
思路
对原数组进行模拟下标x(2n)x(2~n)x(2 n)
根据题目
若ax−1<2⋅axa_{x-1}<2\cdot a_xax−1<2⋅ax
∴fx=1\therefore f_x=1∴fx=1
否则,fx=0f_x=0fx=0
对f数组f数组f数组进行前缀和预处理,就可以实现O(n)\Omicron(n)O(n)时间复杂度的统计了。
代码实现
#include<bits/stdc++.h>
using namespace std;const int maxn=2e5+10;
int t,n,k,ans;
int a[maxn],f[maxn];
int main(){scanf("%d",&t);while(t--){scanf("%d%d",&n,&k);int op=0;ans=0;memset(a,0,sizeof(a));for(int i=1;i<=n;i++){int x;scanf("%d",&x);if(2*x>op)a[i]=1;op=x;}for(int i=1;i<=n;i++){f[i]=f[i-1]+a[i];if(i-k-1<0)continue;if(f[i]-f[i-k]==k)++ans;}printf("%d\n",ans);}return 0;
}
相关文章:

CF1692G 2^Sort 题解
CF1692G 2^Sort 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1692G 字面描述 题面翻译 给你一个长度为 n(∑n<2⋅105)n \ (\sum n < 2\cdot 10^5)n (∑n<…...

关于物理像素,逻辑像素,像素比
关于物理像素、逻辑像素(css像素)、分辨率、像素比的超详细讲解 在日常生活中,有这样一个问题。同样的图片为什么在不同的设备上显示的大小是不一样的。🤒带着这个问题来说明一下。 一、物理像素 设备刚生产出来就已经固定了&a…...

JavaSE基础部分总结
JavaSe基础部分 文章目录JavaSe基础部分1.命名规范2.基本的数据类型3.方法3.1方法的基本格式3.2 方法的分类3.3 方法的注释4.数组4.1 数组的命名格式4.2 数组中存在的址交换的操作4.3数组Arrays常用的方法1. Arrays.asList(数组作为参数或者数据作为参数):2.Arrays.…...

C++基础知识
目录类和对象C static_cast、dynamic_cast、const_cast和reinterpret_cast1、为什么要引入这四种类型转化?2、应用场景。C/C类型转换的本质struct和class的区别为什么会诞生面向对象的编程思想析构函数的执行时机初始化 const 成员变量C const对象(常对象…...
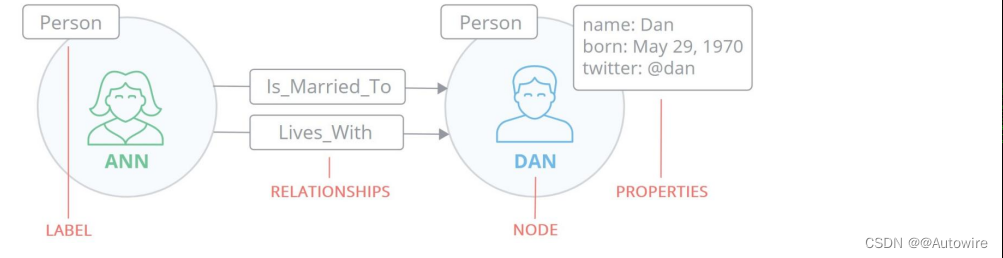
2023/2/24 图数据库Neo4j的理解与应用
1 什么是图数据库(graph database) 十大应用案例:https://go.neo4j.com/rs/710-RRC-335/images/Neo4j-Top-Use-Cases-ZH.pdf “大数据”每年都在增长,但如今的企业领导者不仅需要管理更大规模的数据,还迫切需要从现有…...

适合视力障碍者的Linux
导读有哪些最适合视障用户的 Linux 发行版?让我们一起来看看。 如果有人视力障碍或失明,他们可能会依赖声音提示或其他交互方式(如盲文)来阅读和交流。 他们怎样才能使用 Linux 发行版? 嗯,一般来说&…...

Tina Linux 存储开发指南
Tina Linux 存储开发指南 1 概述 1.1 编写目的 介绍TinaLinux Flash,分区,文件系统等存储相关信息,指导方案的开发定制。 1.2 适用范围 Tina V3.0 及其后续版本。 1.3 相关人员 适用于TinaLinux 平台的客户及相关技术人员。 2 分区管…...
)
【洛谷 P2670】[NOIP2015 普及组] 扫雷游戏 题解(模拟)
[NOIP2015 普及组] 扫雷游戏 题目背景 NOIP2015 普及组 T2 题目描述 扫雷游戏是一款十分经典的单机小游戏。在 nnn 行 mmm 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩家翻…...
【nohup引发磁盘读写高】nohup命令导致服务器磁盘读写占满该如何修复?
【写在前面】自己在跑一个项目的时候,猛然发现服务器挂了,直接访问不了,呈现出一种卡死现象,我当时都懵了,难道阿里在后端升级,也不会选择在工作日的时间升级吧,于是乎就咨询了一下客服。才有下…...

MySQL(二)索引和SQL优化
MySQL进阶MySQL体系结构存储引擎存储引擎特点InnoDB逻辑存储结构MyISAMMemory存储引擎选择索引索引结构二叉树B-TreeBTreeHash索引分类索引语法SQL性能分析工具SQL执行频率慢查询日志profile详情explain索引使用联合索引索引失效情况SQL提示覆盖索引前缀索引单列索引与联合索引…...
Java常用日期类(包含三代)_Date类及Calendar类等
一.java.util.Date类概述从JDK 1.0出现。表示一个日期和时间,精确到毫秒,内部getTime()从1970年1月1号开始算。1. java.util.Date类构造部份构造已经过时,重点看以下两个构造。public Date()从运行程序的此时此刻到时间原点经历的毫秒值&…...

计算机网络你都懂了吗
文章目录一、计算机网络的定义简单定义通用定义二、计算机网络通信过程三、什么是网络协议(Protocol)四、网络协议组成及功能一、计算机网络的定义 简单定义 计算机网络是一些相互连接的、自治的计算机系统的集合。 通用定义 将处于不同位置并具有独…...

3.4 Spring Boot 日志配置
第3章 Spring Boot 的系统配置 3.1 Spring Boot 系统配置文件 3.2 Spring Boot 自定义配置项 3.3 Spring Boot 其他配置 3.4 Spring Boot 日志配置 3.5 实战:Spring Boot 实现系统多环境配置 3.4 Spring Boot 日志配置 日志对于系统监控、故障定位非常重要…...
3款百里挑一的国产软件,逆天好用,装了就舍不得卸载
推荐3款让你偷懒,让你上头的提效电脑软件,个个功能强大,让你远离加班! 很多几个小时才能做好的事情,用上它们,只需要5分钟就行!! 1、JNPF快速开发平台 JNPF 是一款精巧耐用的软件…...
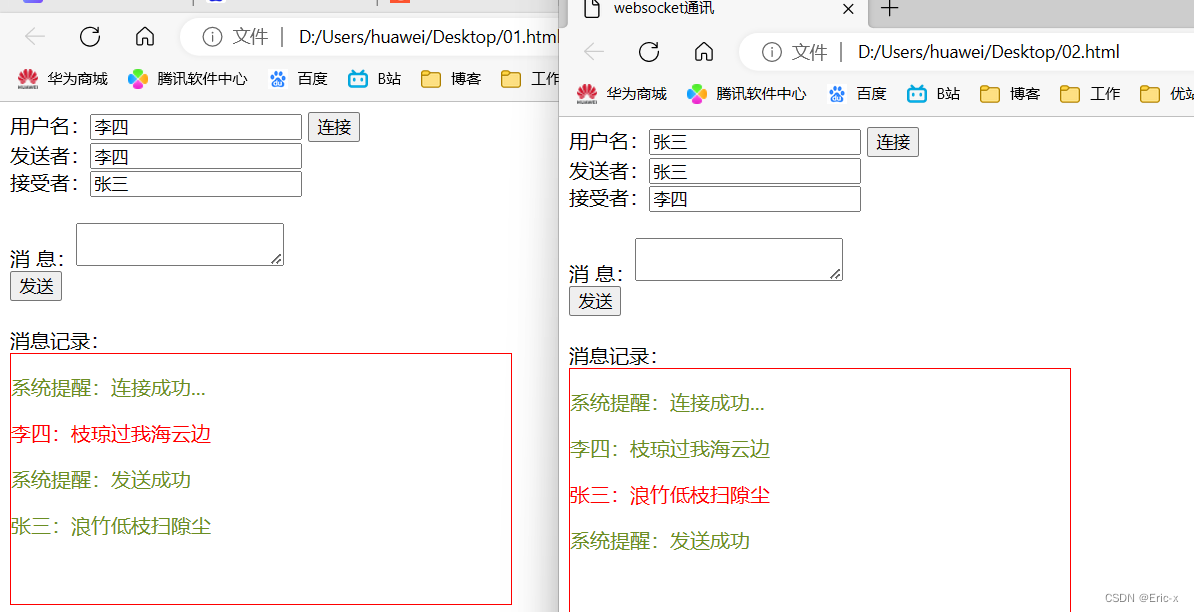
Java实现在线沟通功能
文章目录1、介绍 和 特点2、整合SpringBoot2.1、导入依赖2.2、websocket 配置类2.3、消息处理类2.4、启动服务2.5、前端代码:张三2.6、前端代码:李四3、效果4、小结1、介绍 和 特点 t-io是基于JVM的网络编程框架,和netty属同类,所…...
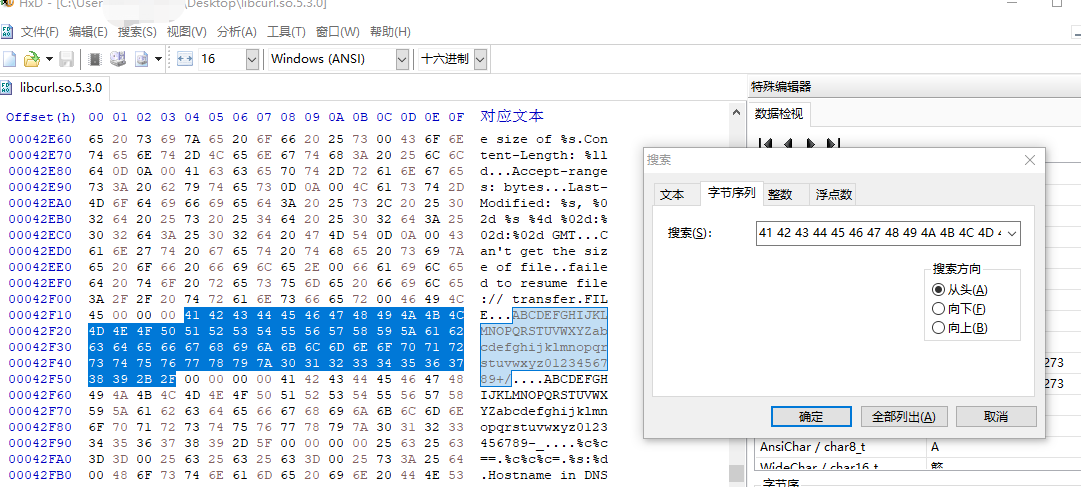
识别密文加密类型
离线密码破解:离线不会触发密码锁定机制不会产生大量登录失败日志引起管理员注意HASH识别工具(识别哈希类型):hash-identifierHashid yara规则匹配文件得到特定加密算法一、hash-identifierKali Linux提供工具hash-identifier来识…...
node报错
记录bug:运行 npx -p storybook/cli sb init 时报错gyp info spawn C:\Program Files\Microsoft Visual Studio\2022\Community\MSBuild\Current\Bin\MSBuild.exegyp info spawn args [gyp info spawn args build/binding.sln,gyp info spawn args /nologo,gyp info spawn args…...
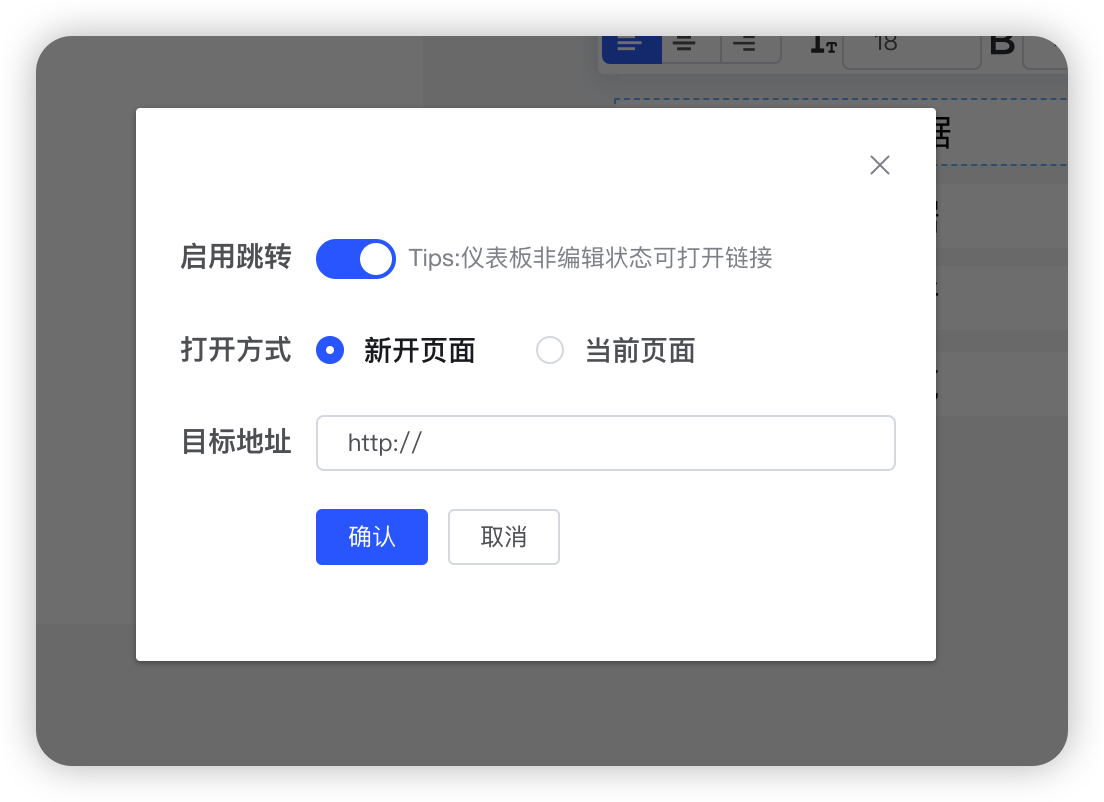
如何使用开源 BI 工具 DataEase 实现系列数据分析呢?
当我们使用可视化分析工具制作仪表板时,可能需要制作的仪表板不是单个单个的可视化大屏,而是一系列的仪表板,我们需要用它来产生一个连续性的故事,那么这个时候我们该怎么办呢?例如说总分形式,我们需要一个…...
金仓数据库安装
一、麒麟操作系统安装金仓数据库 操作系统 DISTRIB_IDKylin DISTRIB_RELEASEV10 DISTRIB_CODENAMEjuniper 按照安装文档的步骤安装,记得记住设置的数据库的用户名、密码 二、window安装连接数据库的工具软件 三、jdbc连接数据库 (1)连接工…...

深入浅出Webpack2-快速掌握webpack基本配置
深入浅出Webpack2-快速掌握webpack基本配置1.Entry1.1 context1.2 Entry类型2.Output2.1 filename2.2 path3.Module3.1配置Loader4.Resolve4.1 alias4.2 extensions4.3 modules5.Plugin6.DevServer7.其他配置项上一篇文章我们快速上手认识了一下webpack,今天这篇文章…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
