pytorch的基本运算,是不是共享了内存,有没有维度变化
-
可以把PyTorch简单看成是Python的深度学习第三方库,在PyTorch中定义了适用于深度学习的基本数据结构——
张量,以及张量的各类计算。其实也就相当于NumPy中定义的Array和对应的科学计算方法,正是这些基本数据类型和对应的方法函数,为我们进一步在PyTorch上进行深度学习建模提供了基本对象和基本工具。因此,在正式使用PyTorch进行深度学习建模之前,我们需要熟练掌握PyTorch中张量的基本操作方法。张量作为数组的衍生概念,其本身的定义和使用方法和NumPy中的Array非常类似,甚至,在复现一些简单的神经网络算法场景中,我们可以直接使用NumPy中的Array来进行操作。 -
张量的最基本创建方法和NumPy中创建Array的格式一致,都是
创建函数(序列)的格式:张量创建函数:torch.tensor()-
t = torch.tensor([[0,1], [2,3]]) # 通过列表创建张量 # 通过元组创建张量 # torch.tensor((1, 2)) # 通过数组创建张量 # a = np.array((1, 2)) # t = torch.tensor(a) # 整数型的数组默认创建int32(整型)类型,而张量则默认创建int64(长整型)类型。 # 创建浮点型数组时,张量默认是float32(单精度浮点型),而Array则是默认float64(双精度浮点型)。 print(t,t.data) print(id(t),id(t.data)) ## 输出 ## tensor([[0, 1],[2, 3]]) tensor([[0, 1],[2, 3]]) 2036011697072 2036018540848 -
两者返回不同的id,但是共享同一个内存
-
t[0][0]=10 t.data[1][0]=20 print(t,t.data) print(id(t),id(t.data)) ## 输出 ## tensor([[10, 1],[20, 3]]) tensor([[10, 1],[20, 3]]) 2036011697072 2036019332576 -
属性 grad(导数), grad-fn(张量所在的导数函数), requires_grad(是否执行可导的判定)。调用backward计算导数,导数是累加的,如果每次单独计算,需要清空梯度
optimiter.zero_grad()。 -
属性 is_leaf, retain_grad。判定该元素在计算图中是否为叶子节点,当为叶子节点时,它的属性requires_grad为False。当requires_grad为True,但是用户构建的Tensor,表示该张量不是计算结果,而是用户构建的初始化张量。在用backward后,仅只有 leaf tensor 才会有 grad 属性。如果不是 leaf tensor 需要retain_grad 函数开启grad。
-
属性ndim和dim函数,查看tensor的维度;属性shape和size(),tensor的形状
-
t=torch.cat([t,t],0) print(t.ndim,len(t),t.dim()) print(t.shape,t.size()) ## 输出 ## 2 8 2 torch.Size([8, 2]) torch.Size([8, 2]) -
和数组不同,对于张量而言,数值型和布尔型张量就是最常用的两种张量类型,相关类型总结如下。
-
数据类型 dtype 32bit浮点数 torch.float32或torch.float 64bit浮点数 torch.float64或torch.double 16bit浮点数 torch.float16或torch.half 8bit无符号整数 torch.unit8 8bit有符号整数 torch.int8 16bit有符号整数 torch.int16或torch.short 32bit有符号整数 torch.int32或torch.int 64bit有符号整数 torch.int64或torch.long 布尔型 torch.bool 复数型 torch.complex64
-
-
创建int16整型张量; torch.tensor([1.1, 2.7], dtype = torch.int16)
-
在PyTorch中也支持复数类型对象创建; a = torch.tensor(1 + 2j) # 1是实部、2是虚部; tensor(1.+2.j)
-
和NumPy中array相同,当张量各元素属于不同类型时,系统会自动进行隐式转化。在使用方法进行类型转化时,方法名称则是double。(虽然torch.float和double都表示双精度浮点型。)
-
-
flatten拉平:将任意维度张量转化为一维张量,按行排列,拉平。注:如果将零维张量使用flatten,则会将其转化为一维张量。
-
reshape方法:任意变形;注意,reshape过程中维度的变化:reshape转化后的维度由该方法输入的参数“个数”决定。
-
在很多数值科学计算的过程中,都会创建一些特殊取值的张量,用于模拟特殊取值的矩阵,如全0矩阵、对角矩阵等。因此,PyTorch中也存在很多创建特殊张量的函数。
-
torch.zeros([2, 3]) # 创建全是0的,两行、三列的张量(矩阵) torch.ones([2, 3]) # 注:由于zeros就已经确定了张量元素取值,因此该函数传入的参数实际上是决定了张量的形状 -
单位矩阵
-
torch.eye(5) ## tensor([[1., 0., 0., 0., 0.],[0., 1., 0., 0., 0.],[0., 0., 1., 0., 0.],[0., 0., 0., 1., 0.],[0., 0., 0., 0., 1.]]) -
在PyTorch中,需要利用一维张量去创建对角矩阵。
-
t1 = torch.tensor([1, 2]) torch.diag(t1) # 不能使用list直接创建对角矩阵,diag(): argument 'input' (position 1) must be Tensor, not list ## tensor([[1, 0],[0, 2]]) -
rand:服从0-1均匀分布的张量
-
torch.randn(2, 3) torch.normal(2, 3, size = (2, 2)) # 均值为2,标准差为3的张量;normal:服从指定正态分布的张量 torch.randint(1, 10, [2, 4]) # 在1-10之间随机抽取整数,组成两行四列的矩阵,randint:整数随机采样结果 -
arange/linspace:生成数列
-
torch.arange(5) # 和range相同;tensor([0, 1, 2, 3, 4]) torch.arange(1, 5, 0.5) # 从1到5(左闭右开),每隔0.5取值一个 torch.linspace(1, 5, 3) # 从1到5(左右都包含),等距取三个数;tensor([1., 3., 5.]) -
empty:生成未初始化的指定形状矩阵
-
torch.empty(2, 3) ## tensor([[6.8664e-44, 6.8664e-44, 1.1771e-43],[6.7262e-44, 7.0065e-44, 8.1275e-44]]) torch.full([2, 4], 2) tensor([[2, 2, 2, 2],[2, 2, 2, 2]]) -
还能根据指定对象的形状进行数值填充,只需要在上述函数后面加上
_like即可。 -
torch.full_like(t1, 2) # 根据t1形状,填充数值2 torch.randint_like(t2, 1, 10) # 根据t1形状,填充数值1-10,不包括10的整数 t1 = torch.tensor([1, 2]) torch.randn_like(t1) # t1是整数,而转化后将变为浮点数,此时代码将报错,"normal_kernel_cpu" not implemented for 'Long' -
张量、数组和列表是较为相似的三种类型对象,在实际操作过程中,经常会涉及三种对象的相互转化。在此前张量的创建过程中,我们看到torch.tensor函数可以直接将数组或者列表转化为张量,而我们也可以将张量转化为数组或者列表。
-
t1 = torch.tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) t1.numpy() # array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=int64) import numpy as np # 当然,也可以通过np.array函数直接转化为array np.array(t1) # array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=int64) t1# tensor([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) # .tolist方法:张量转化为列表 t1.tolist() # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] -
list函数:张量转化为列表
-
[tensor(1),tensor(2),tensor(3),tensor(4),tensor(5),tensor(6),tensor(7),tensor(8),tensor(9),tensor(10)] # 需要注意的是,此时转化的列表是由一个个零维张量构成的列表,而非张量的数值组成的列表。 -
在很多情况下,我们需要将最终计算的结果张量转化为单独的数值进行输出,此时需要使用.item()方法来执行。
-
Python中其他对象类型一样,等号赋值操作实际上是浅拷贝,需要进行深拷贝,则需要使用clone方法
-
-
张量作为有序的序列,也是具备数值索引的功能,并且基本索引方法和Python原生的列表、NumPy中的数组基本一致,当然,所有不同的是,PyTorch中还定义了一种采用函数来进行索引的方式。张量也是有序序列,我们可以根据每个元素在系统内的顺序“编号”,来找出特定的元素,也就是索引。张量索引出来的结果还是零维张量, 而不是单独的数。要转化成单独的数,需要使用item()方法。
在张量的索引中,step位必须大于0 -
二维张量的索引逻辑和一维张量的索引逻辑基本相同,二维张量可以视为两个一维张量组合而成,而在实际的索引过程中,需要用逗号进行分隔,分别表示对哪个一维张量进行索引、以及具体的一维张量的索引。对二维张量来说,基本可以视为是对矩阵的索引,并且行、列的索引遵照相同的索引规范,并用逗号进行分隔。
-
import torch t2 = torch.arange(1, 10).reshape(3, 3) t2 t2[0, 1] # 表示索引第一行、第二个(第二列的)元素 tensor(2) t2[0][1]# 表示索引第一行、第二个(第二列的)元素 tensor(2) t2[0, ::2]# 表示索引第一行、每隔两个元素取一个 tensor([1, 3]) t2[0, [0, 2]] # 索引结果同上 t2[::2, ::2] # 表示每隔两行取一行、并且每一行中每隔两个元素取一个 tensor([[1, 3],[7, 9]])
-
-
在二维张量索引的基础上,三维张量拥有三个索引的维度。我们将三维张量视作矩阵组成的序列,则在实际索引过程中拥有三个维度,分别是索引矩阵、索引矩阵的行、索引矩阵的列。
-
t3 = torch.arange(1, 28).reshape(3, 3, 3) t3 ## tensor([[[ 1, 2, 3],[ 4, 5, 6],[ 7, 8, 9]],[[10, 11, 12],[13, 14, 15],[16, 17, 18]],[[19, 20, 21],[22, 23, 24],[25, 26, 27]]]) t3[1, ::2, ::2] # 索引第二个矩阵,行和列都是每隔两个取一个 tensor([[10, 12],[16, 18]]) t3[:: 2, :: 2, :: 2] # 每隔两个取一个矩阵,对于每个矩阵来说,行和列都是每隔两个取一个 tensor([[[ 1, 3],[ 7, 9]],[[19, 21],[25, 27]]])
-
-
在PyTorch中,我们还可以使用index_select函数,通过指定index来对张量进行索引。在index_select函数中,第二个参数实际上代表的是索引的维度。对于t1这个一维向量来说,由于只有一个维度,因此第二个参数取值为0,就代表在第一个维度上进行索引。
-
t1 = torch.arange(10) indices = torch.tensor([1, 2]) # 需要tensor torch.index_select(t1, 0, indices) ## tensor([1, 2]) t2 = torch.arange(12).reshape(4, 3) ## tensor([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]]) torch.index_select(t2, 0, indices) ## tensor([[3, 4, 5],[6, 7, 8]])
-
-
在正式介绍张量的切分方法之前,需要首先介绍PyTorch中的.view()方法。该方法会返回一个类似视图的结果,该结果和原张量对象共享一块数据存储空间,并且通过.view()方法,还可以改变对象结构,生成一个不同结构,但共享一个存储空间的张量。当然,共享一个存储空间,也就代表二者是“浅拷贝”的关系,修改其中一个,另一个也会同步进行更改。“视图”的作用就是节省空间,而值得注意的是,在接下来介绍的很多切分张量的方法中,返回结果都是“视图”,而不是新生成一个对象。
-
chunk函数能够按照某维度,对张量进行均匀切分,并且返回结果是原张量的视图。
-
t2 = torch.arange(12).reshape(4, 3) tc = torch.chunk(t2, 4, dim=0) # 在第零个维度上(按行),进行四等分 ## 返回类型是元组 (tensor([[0, 1, 2]]),tensor([[3, 4, 5]]),tensor([[6, 7, 8]]),tensor([[ 9, 10, 11]]))# chunk返回结果是一个视图,不是新生成了一个对象# 修改tc中的值,原张量也会对应发生变化 -
当原张量不能均分时,chunk不会报错,但会返回其他均分的结果
-
torch.chunk(t2, 3, dim=0) # 次一级均分结果 ## (tensor([[0, 1, 2],[3, 4, 5]]),tensor([[ 6, 7, 8],[ 9, 10, 11]]))
-
-
split既能进行均分,也能进行自定义切分。当然,需要注意的是,和chunk函数一样,split返回结果也是view。
-
t2 = torch.arange(12).reshape(4, 3) torch.split(t2, 2, 0) # 第二个参数只输入一个数值时表示均分,第三个参数表示切分的维度 torch.split(t2, [1, 3], 0)# 第二个参数输入一个序列时,表示按照序列数值进行切分,也就是1/3分 ## (tensor([[0, 1, 2]]),tensor([[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])) torch.split(t2, [1, 1, 2], 0) ## (tensor([[0, 1, 2]]),tensor([[3, 4, 5]]),tensor([[ 6, 7, 8],[ 9, 10, 11]])) -
注意,当第二个参数位输入一个序列时,序列的各数值的和必须等于对应维度下形状分量的取值。例如,上述代码中,是按照第一个维度进行切分,而t2总共有4行,因此序列的求和必须等于4,也就是1+3=4,而序列中每个分量的取值,则代表切块大小。tensor的split方法和array的split方法有很大的区别,array的split方法是根据索引进行切分。
-
import numpy as np x = np.array([0,1,2,3,4,5,6,7,8]) print (np.split(x,[3,5,6,9])) ## [array([0, 1, 2]), array([3, 4]), array([5]), array([6, 7, 8]), array([], dtype=int32)]
-
-
张量的合并操作类似与列表的追加元素,可以拼接、也可以堆叠。PyTorch中,可以使用cat函数实现张量的拼接。
-
a = torch.zeros(2, 3) b = torch.ones(2, 3) c = torch.full((3, 3),2) torch.cat([a, b]) # 按照行进行拼接,dim默认取值为0 ## tensor([[0., 0., 0.],[0., 0., 0.],[1., 1., 1.],[1., 1., 1.]]) torch.cat([a, b], 1) # 按照列进行拼接 tensor([[0., 0., 0., 1., 1., 1.],[0., 0., 0., 1., 1., 1.]]) torch.cat([a, c], 1) # 形状不匹配时将报错 # Sizes of tensors must match except in dimension 1. Expected size 2 but got size 3 for tensor number 1 in the list. -
拼接的本质是实现元素的堆积,也就是构成a、b两个二维张量的各一维张量的堆积,最终还是构成二维向量。
-
-
堆叠函数:stack;和拼接不同,堆叠不是将元素拆分重装,而是简单的将各参与堆叠的对象分装到一个更高维度的张量里。
-
torch.stack([a, b]) # 堆叠之后,生成一个三维张量 tensor([[[0., 0., 0.],[0., 0., 0.]],[[1., 1., 1.],[1., 1., 1.]]]) torch.stack([a, b]).shape # torch.Size([2, 2, 3]) torch.stack([a, c]) # 维度不匹配时也会报错 # stack expects each tensor to be equal size, but got [2, 3] at entry 0 and [3, 3] at entry 1
-
-
通过reshape方法,能够灵活调整张量的形状。而在实际操作张量进行计算时,往往需要另外进行降维和升维的操作,当我们需要除去不必要的维度时,可以使用squeeze函数,而需要手动升维时,则可采用unsqueeze函数。
-
t = torch.zeros(1, 1, 3, 1) #t张量解释:一个包含一个三维的四维张量,三维张量只包含一个三行一列的二维张量。 ## tensor([[[[0.],[0.],[0.]]]]) torch.squeeze(t) # tensor([0., 0., 0.]) torch.squeeze(t).shape # torch.Size([3]) t1 = torch.zeros(1, 1, 3, 2, 1, 2) ## tensor([[[0., 0.],[0., 0.]],[[0., 0.],[0., 0.]],[[0., 0.],[0., 0.]]]) torch.squeeze(t1).shape # torch.Size([3, 2, 2]) -
简单理解,squeeze就相当于提出了shape返回结果中的1。unsqeeze函数:手动升维
-
torch.unsqueeze(t, dim = 0) # 在第1个维度索引上升高1个维度 torch.unsqueeze(t, dim = 2).shape # 在第3个维度索引上升高1个维度 torch.unsqueeze(t, dim = 4).shape # 在第5个维度索引上升高1个维度 -
注意理解维度和shape返回结果一一对应的关系,shape返回的序列有几个元素,张量就有多少维度。
-
-
作为PyTorch中执行深度学习的基本数据类型,张量(Tensor)也拥有非常多的数学运算函数和方法,以及对应的一系列计算规则。在PyTorch中,能够作用与Tensor的运算,被统一称作为算子。并且相比于NumPy,PyTorch给出了更加规范的算子(运算)的分类,从而方便用户在不同场景下调用不同类型的算子(运算)。PyToch总共为Tensor设计了六大类数学运算,分别是:
-
逐点运算(Pointwise Ops):指的是针对Tensor中每个元素执行的相同运算操作;
-
规约运算(Reduction Ops):指的是对于某一张量进行操作得出某种总结值;
-
比较运算(Comparison Ops):指的是对多个张量进行比较运算的相关方法;
-
谱运算(Spectral Ops):指的是涉及信号处理傅里叶变化的操作;
-
BLAS和LAPACK运算:指的是基础线性代数程序集(Basic Linear Algeria Subprograms)和线性代数包(Linear Algeria Package)中定义的、主要用于线性代数科学计算的函数和方法;
-
其他运算(Other Ops):其他未被归类的数学运算。
-
t1 = torch.arange(3) t = t1+t1 # tensor([0, 2, 4]) a=[2,3,4]+[1,2,3] # [2, 3, 4, 1, 2, 3] import numpy as np b=np.arange(3)+np.arange(3) # array([0, 2, 4]) -
广播的特性是在不同形状的张量进行计算时,一个或多个张量通过隐式转化,转化成相同形状的两个张量,从而完成计算的特性。但并非任何两个不同形状的张量都可以通过广播特性进行计算,因此,我们需要了解广播的基本规则及其核心依据。标量可以和任意形状的张量进行计算,计算过程就是标量和张量的每一个元素进行计算。
-
t1 + 1 # 1是标量,可以看成是零维 tensor([1, 2, 3]) t1 + torch.tensor(1) #tensor([1, 2, 3]) -
相同维度、不同形状的张量之间计算;两个张量的形状上有两个分量不同时,只要不同的分量仍然有一个取值为1,则仍然可以广播。
-

-
在理解相同维度、不同形状的张量广播之后,对于不同维度的张量之间的广播其实就会容易很多,因为对于不同维度的张量,我们首先可以将低维的张量升维,然后依据相同维度不同形状的张量广播规则进行广播。而低维向量的升维也非常简单,只需将更高维度方向的形状填充为1即可。
-
-
逐点运算主要包括数学基本运算、数值调整运算和数据科学运算三块,相关函数如下:
-
函数 描述 torch.add(t1,t2 ) t1、t2两个张量逐个元素相加,等效于t1+t2 torch.subtract(t1,t2) t1、t2两个张量逐个元素相减,等效于t1-t2 torch.multiply(t1,t2) t1、t2两个张量逐个元素相乘,等效于t1*t2 torch.divide(t1,t2) t1、t2两个张量逐个元素相除,等效于t1/t2 -
函数 描述 torch.abs(t) 返回绝对值 torch.ceil(t) 向上取整 torch.floor(t) 向下取整 torch.round(t) 四舍五入取整 torch.neg(t) 返回相反的数 -
虽然此类型函数是数值调整函数,但并不会对原对象进行调整,而是输出新的结果。而若要对原对象本身进行修改,则可考虑使用
方法_()的表达形式,对对象本身进行修改。此时方法就是上述同名函数。 -
数学运算函数 数学公式 描述 幂运算 torch.exp(t) $ y_{i} = e^{x_{i}} $ 返回以e为底、t中元素为幂的张量 torch.expm1(t) $ y_{i} = e^{x_{i}} $ - 1 对张量中的所有元素计算exp(x) - 1 torch.exp2(t) $ y_{i} = 2^{x_{i}} $ 逐个元素计算2的t次方。 torch.pow(t,n) $\text{out}_i = x_i ^ \text{exponent} $ 返回t的n次幂 torch.sqrt(t) $ \text{out}{i} = \sqrt{\text{input}{i}} $ 返回t的平方根 torch.square(t) $ \text{out}_i = x_i ^ \text{2} $ 返回输入的元素平方。 对数运算 torch.log10(t) $ y_{i} = \log_{10} (x_{i}) $ 返回以10为底的t的对数 torch.log(t) $ y_{i} = \log_{e} (x_{i}) $ 返回以e为底的t的对数 torch.log2(t) $ y_{i} = \log_{2} (x_{i}) $ 返回以2为底的t的对数 torch.log1p(t) $ y_i = \log_{e} (x_i $ + 1) 返回一个加自然对数的输入数组。 三角函数运算 torch.sin(t) 三角正弦。 torch.cos(t) 元素余弦。 torch.tan(t) 逐元素计算切线。 -
在数值科学计算中,expm1函数和log1p函数是一对对应的函数关系,后面再介绍log1p的时候会讲解这对函数的实际作用。开根号也就相当于0.5次幂
-
log1p是进行$ y_i = \log_{e} (x_i $ + 1)计算,而expm则是进行$ y_{i} = e^{x_{i}} $ - 1计算,二者互为逆运算。
-
-
需要注意的是,虽然Python是动态编译的编程语言,但在PyTorch中,由于会涉及GPU计算,因此很多时候元素类型不会在实际执行函数计算时进行调整。此处的科学运算大多数都要求对象类型是浮点型,我们需要提前进行类型转化。
-
而log1p的实际应用场景有两个,其一是进行数据分布转化操作,另一种则是防止极小的数在进行对数运算时丢失有效位数。
-
大多数的数理统计分析,在建模过程中,都对数据的分布有较为严格的要求,但真实的数据往往不能满足特定的分布,因此很多时候我们会先对其进行一定程度上的数值转化,而log运算就是常用的将偏态分布的数据转化为高斯分布所使用的函数,并且在此过程中,log1p的效果往往会好于log的效果;
-
另一种使用场景,当处理的数据数值非常小时,使用对数运算往往会因为精度不够而使得计算无法进行(log0没有数学意义),此时使用log1p则可很好的避免这种情况。
-
m = torch.tensor(-2.6529) * 1e-20 # tensor(-2.6529e-20) # 转化为一个趋近于1的数再运算 torch.log1p(m) # tensor(-2.6529e-20) # 此时直接使用log无法执行运算 torch.log(m) # tensor(nan) # 无法运算就无法还原 torch.exp(torch.log(m)) # tensor(nan) # 无损还原 torch.expm1(torch.log1p(m)) # tensor(-2.6529e-20) -
在很多场景中,由于计算精度问题导致无法计算,并进一步导致数据信息损失,将会是非常致命的,典型场景如PCA主成分分析,相关问题会在算法讲解中进一步讨论。
-
-
在PyTorch中,sort排序函数将同时返回排序结果和对应的索引值的排列。
-
t = torch.tensor([1.0, 3.0, 2.0]) # 升序排列 torch.sort(t) ## torch.return_types.sort( values=tensor([1., 2., 3.]), indices=tensor([0, 2, 1])) # 降序排列 torch.sort(t, descending=True) ## torch.return_types.sort( values=tensor([3., 2., 1.]), indices=tensor([1, 2, 0]))
-
-
规约运算指的是针对某张量进行某种总结,最后得出一个具体总结值的函数。此类函数主要包含了数据科学领域内的诸多统计分析函数,如均值、极值、方差、中位数函数等等。
-
函数 描述 torch.mean(t) 返回张量均值 torch.var(t) 返回张量方差 torch.std(t) 返回张量标准差 torch.var_mean(t) 返回张量方差和均值 torch.std_mean(t) 返回张量标准差和均值 torch.max(t) 返回张量最大值 torch.argmax(t) 返回张量最大值索引 torch.min(t) 返回张量最小值 torch.argmin(t) 返回张量最小值索引 torch.median(t) 返回张量中位数 torch.sum(t) 返回张量求和结果 torch.logsumexp(t) 返回张量各元素求和结果,适用于数据量较小的情况 torch.prod(t) 返回张量累乘结果 torch.dist(t1, t2) 计算两个张量的闵式距离,可使用不同范式; torch.dist(t1, t2, 2) torch.topk(t) 返回t中最大的k个值对应的指标; torch.topk(t, 2)
-
-
dist函数可计算闵式距离(闵可夫斯基距离),通过输入不同的p值,可以计算多种类型的距离,如欧式距离、街道距离等。闵可夫斯基距离公式如下: $ D(x,y) = (\sum{n}_{u=1}|x_u-y_u|{p})^{1/p}$
-
由于规约运算是一个序列返回一个结果,因此若是针对高维张量,则可指定某维度进行计算。
-
# 创建一个3*3的二维向量 t2 = torch.arange(12).float().reshape(3, 4) # 按照第一个维度求和(每次计算三个)、按列求和 torch.sum(t2, dim = 0) # tensor([12., 15., 18., 21.]) # 按照第二个维度求和(每次计算四个)、按行求和 torch.sum(t2, dim = 1) # tensor([ 6., 22., 38.])
-
-
比较运算是一类较为简单的运算类型,和Python原生大的布尔运算类似,常用于不同张量之间的逻辑运算,最终返回逻辑运算结果(逻辑类型张量)。基本比较运算函数如下所示:
-
函数 描述 torch.eq(t1, t2) 比较t1、t2各元素是否相等,等效== torch.equal(t1, t2) 判断两个张量是否是相同的张量 torch.gt(t1, t2) 比较t1各元素是否大于t2各元素,等效> torch.lt(t1, t2) 比较t1各元素是否小于t2各元素,等效< torch.ge(t1, t2) 比较t1各元素是否大于或等于t2各元素,等效>= torch.le(t1, t2) 比较t1各元素是否小于等于t2各元素,等效<= torch.ne(t1, t2) 比较t1、t2各元素是否不相同,等效!=
-
相关文章:

pytorch的基本运算,是不是共享了内存,有没有维度变化
可以把PyTorch简单看成是Python的深度学习第三方库,在PyTorch中定义了适用于深度学习的基本数据结构——张量,以及张量的各类计算。其实也就相当于NumPy中定义的Array和对应的科学计算方法,正是这些基本数据类型和对应的方法函数,…...
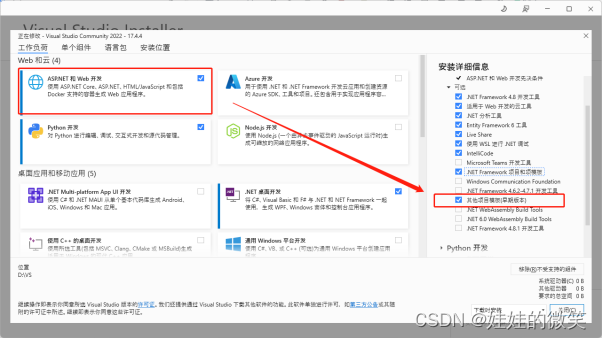
Visual Studio 2022新建项目时没有ASP.NET项目
一、Visual Studio 2022新建项目时没有ASP.NET项目 1、打开VS开发工具,选择工具菜单,点击“获取工具和功能” 2、选择“ASP.NET和Web开发”和把其他项目模板(早期版本)勾选上安装即可...

nuiapp项目实战:导航栏动态切换效果实践案例树
测试软件的百忙之中去进行软件开发的工作,开展开发软件的工作事情,也真是繁忙至极点的了。 不到一刻钟的课程内容,个人用了三次去写串联的知识点,然后这是第三次,还是第四次了才完全写出来一个功能的效果。 一刻钟的功…...

【机器学习】集成学习(以随机森林为例)
文章目录 集成学习随机森林随机森林回归填补缺失值实例:随机森林在乳腺癌数据上的调参附录参数 集成学习 集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通过在数据…...
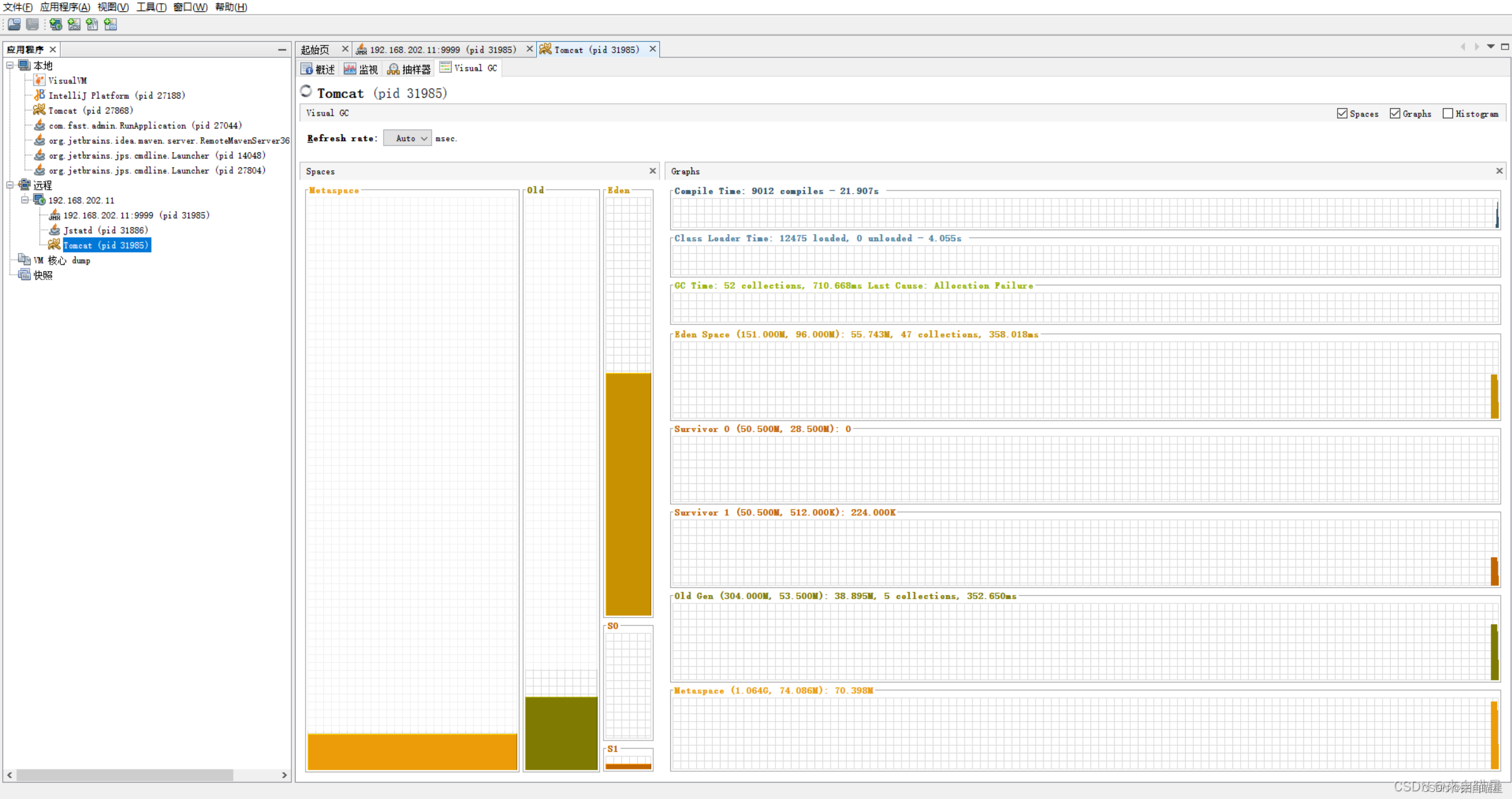
主机jvisualvm连接到tomcat服务器查看jvm状态
使用JMX方式连接到tomcat,连接后能够查看前边的部分内容,但是不能查看Visual GC,显示不受此JVM支持, 对了,要显示Visual GC,首先要安装visualvm工具,具体安装方式就是根据自己的jdk版本下载…...

uniapp 自定义tabbar页面不刷新
最近在做自定义tabbar时,每次切换页面都要刷新,页面渲染很慢,需要实现切换页面不刷新问题。 结局思路,原生的tabbar切换页面时就不选新,用switchTab来跳转 1.pages.json中配置tabbar,如下,设置高度为0&am…...

3.1 SQL概述
思维导图: 前言: 前言笔记:第3章 关系数据库标准语言SQL - **SQL的定义**: - 关系数据库的标准和通用语言。 - 功能强大,不仅限于查询。 - 功能覆盖:数据库模式创建、数据插入/修改、数据库安全性与…...
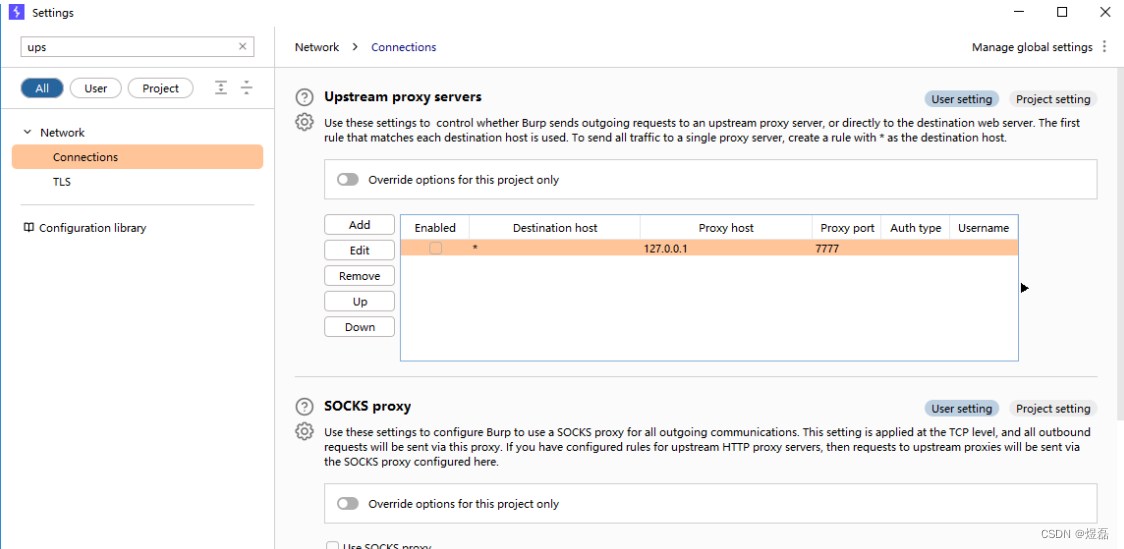
xray安装与bp组合使用-被动扫描
xray安装与bp组合使用-被动扫描 文章目录 xray安装与bp组合使用-被动扫描1 工具官方文档:2 xray官网3 工具使用4 使用指令说明5 此为设置被动扫描6 被动扫描-启动成功7 启动bp7.1 设置bp的上层代理7.2 添加上层代理7777 --》指向的是xray7.3 上层代理设置好后&#…...

Java 中Maven 和 ANT
Java 中Maven 和 ANT Maven 和 Ant 都是用于构建和管理Java项目的工具,但它们在设计和功能上有一些重要的区别。以下是关于 Maven 和 Ant 的区别、优缺点以及它们的作用,以及示例说明: Maven: 设计理念: Maven 是基于…...

Flutter通过Pigeon插件与Android同步异步交互
Flutter 调用原生(Android)方法以及数据传输_flutter调用原生sdk_TDSSS的博客-CSDN博客 https://www.cnblogs.com/baiqiantao/p/16340272.html 可以同时参考这两篇文章...

GTW验厂是什么?GTW验厂评级分类
【GTW验厂是什么?GTW验厂评级分类】 GTW验厂是什么? 全称叫GreenToWear。是为了集合所有环境和产品健康方面的要求,Inditex集团开发的可持续发展准则(简称GTW)此准则适用于Inditex集 及其供应链中所包含的湿加工厂&…...

CVE-2017-12615 Tomcat远程命令执行漏洞
漏洞简介 2017年9月19日,Apache Tomcat官方确认并修复了两个高危漏洞,漏洞CVE编号:CVE-2017-12615和CVE-2017-12616,其中 远程代码执行漏洞(CVE-2017-12615) 当 Tomcat 运行在 Windows 主机上,…...

灿芯股份将上会:计划募资6亿元,董事长、总经理均为外籍
10月11日,上海证券交易所披露的信息显示,灿芯半导体(上海)股份有限公司(下称“灿芯股份”)将于10月18日接受上市审核委员会审议会议的现场审议。目前,该公司已递交了招股书(上会稿&a…...

Spring Cloud Gateway 搭建网关
新建一个module添加依赖: <!--Spring Cloud Gateway依赖--> <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifactId> </dependency><!-- nacos客户端依赖…...
ETL数据转换方式有哪些
ETL数据转换方式有哪些 ETL(Extract, Transform, Load)是一种常用的数据处理方式,用于从源系统中提取数据,进行转换,并加载到目标系统中。 数据清洗(Data Cleaning)&am…...

CVE-2017-15715 apache换行解析文件上传漏洞
影响范围 httpd 2.4.0~2.4.29 复现环境 vulhub/httpd/CVE-2017-15715 docker-compose 漏洞原理 在apache2的配置文件: /etc/apache2/conf-available/docker-php.conf 中,php的文件匹配以正则形式表达 ".php$"的正则匹配模式意味着以.ph…...

振弦采集仪应用水坝安全监测的方案
振弦采集仪应用水坝安全监测的方案 随着工业化和城市化的快速发展,水资源的开发和利用越来越广泛。由于水坝在水利工程中起着至关重要的作用,因此对水坝进行安全监测变得越来越必要。为了实现对水坝的安全监测,振弦采集仪可以作为一种有效的…...

【Java】查找jdk步骤
需求描述 解决方法 第一步 第二步 第三步 第四步 参考文章...
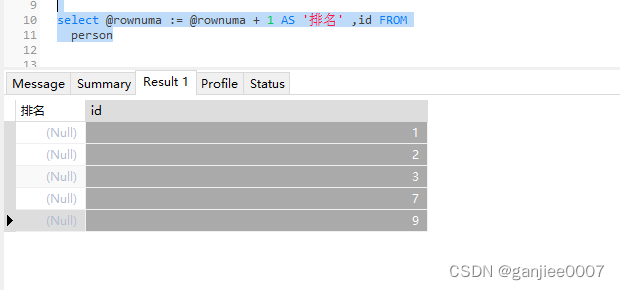
【mysql】Mysql自定义变量 @rownum使用
Mysql自定义变量 rownum 这个可以赋值?这是初始化? 先看表结构 有五条数据。执行前半段语句发现。rownum的起始值等于行数 这里from后面可以加person与 r这连个组成 如果这里的rownum打错了呢。发现这个变量就没有初始值。 可见,没有必要…...

命令行启动android模拟器
有时候不想打开android studio就能方便的启动模拟器,探索一番后发现可以通过命令行来启动,方便快捷。 环境准备 首先安装好android studio,android sdk,从android studio中安装好模拟器。 命令启动 如果直接在终端输入emulato…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
