数学建模——确定性时间序列分析方法
目录
介绍
确定性时间序列分析方法
1、时间序列的常见趋势
(1)长期趋势
(2)季节变动
(3)循环变动
(4)不规则变动
常见的时间序列模型有以下几类
2、时间序列预测的具体方法
2.1 移动平均法
案例1
【符号说明】
【预测模型】
2.2 一次指数平滑预测法
(1)预测模型
(2)加权系数的选择
(3)初始值的确定
案例2
3、差分指数平滑法
案例3
4、具有季节性特点的时间序列的预测
案例4
介绍
将预测对象按照时间顺序排成一组序列,称为时间序列。从时间序列过去的变化规律,推断今后变化的可能性及变化趋势、变化规律,这就是时间序列预测法。
时间序列模型,其实也是一种回归模型。其基本原理是,一方面承认事物发展的延续性,运用过去时间序列进行统计分析就能推断事物发展趋势;另一方面又充分考虑到偶然因素影响产生的随机性,为了消除随机波动的影响,利用历史数据,进行统计分析,并对数据做适当的处理,进行趋势预测。
- 优点:简单易行,便于掌握,能重复利用时间序列各项数据,计算速度快,对模型参数动有态确定能力,精度较好。
- 缺点 : 不能反映事物内在联系,不能分析两个因素的相关关系,只适合作短期预测。
确定性时间序列分析方法
1、时间序列的常见趋势
(1)长期趋势
时间序列朝着一定的方向持续上升或下降或留在某个水平的倾向。它反映了客观事物主要变化趋势,记为Tt;
(2)季节变动
序列按时间呈现短周期变化的规律,记为St;
(3)循环变动
通常是周期为一年以上的,由非季节因素一起的起伏波相似的波动,记为Ct;
(4)不规则变动
通常分为突然变动和随机扰动(变动),记为Rt。
常见的时间序列模型有以下几类
- 加法模型 yt=Tt+St+Ct+Rt;(常用)
- 乘法模型 yt=Tt×St×Ct×Rt;
- 混合模型 yt=Tt×St+Rt;yt=St+Tt×Ct×Rt;
其中,yt为观测值,随机变动Rt满足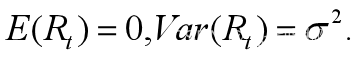
如果在预测时间范围内,无突然变动或者随机波动的方差σ2较小,并且有理由认为现在的演变趋势将持续发展到未来,可用一些经验方法进行预测。
2、时间序列预测的具体方法
2.1 移动平均法
设观测时间序列为y1,y2,…,yT。
一次移动平均值计算公式: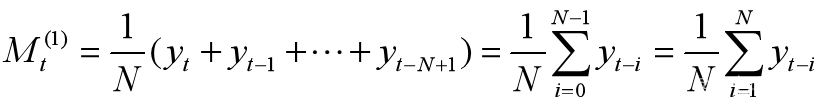
二次移动平均值计算公式: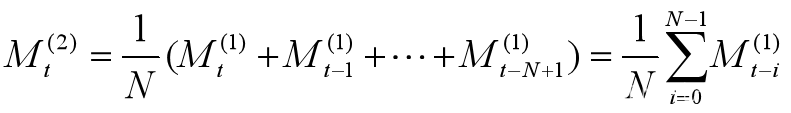
这里N<T,一般5≤N≤200.
(1)当预测目标的基本趋势在某一水平上下波动时,采用一次移动平均方法计算预测,即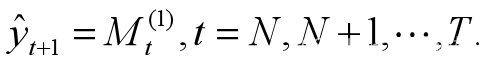
(2)当预测目标的基本趋势与某一直线相吻合时,采用二次移动平均法.
以上预测标准误差为 
一般来说,N取多少为好,S越小越好。如果数据自带周期,N最好取周期值。
案例1
某企业1-11月的销售收入时间序列如表1所列,试用一次移动平均法预测12月的销售收入。
表1 1-11月销售收入记录
| 月份t | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售收入yt | 533.8 | 574.6 | 606.9 | 649.8 | 705.1 | 772.0 |
| 月份t | 7 | 8 | 9 | 10 | 11 | |
| 销售收入yt | 816.4 | 892.7 | 963.9 | 1015.1 | 1102.7 |
【符号说明】
- t 时间变量t=1,2,…,11
- yt 销售量记录值
- n 移动平均项数
- Mt 一次移动平均值,t=n,n+1,…,11
- y(1) 预测值,t=5,6,…,12
【预测模型】
一次移动平均预测模型为: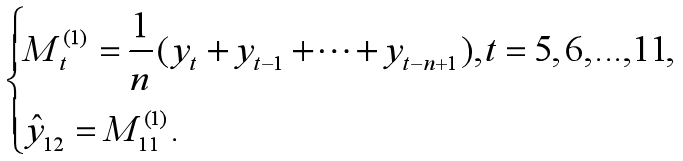
针对n=3,4,5,都做一次移动平均预测,将计算结果和误差都反映在表2.
先编写一个时间序列为yt,移动平均项n的预测与误差的程序yd1.m,再调用此函数计算不同n值的预测与误差,存放在表2进行对比
表2 n分别取3,4,5的预测对比
| t | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 标准误差 |
| yt | 705.10 | 772.00 | 816.40 | 892.70 | 963.90 | 1015.10 | 1102.70 | 0.00 |
| n=3 | 653.93 | 708.97 | 764.50 | 827.03 | 891.00 | 957.23 | 1027.23 | 60.73 |
| n=4 | 634.10 | 683.45 | 735.83 | 796.55 | 861.25 | 922.03 | 993.60 | 92.37 |
| n=5 | 614.04 | 661.68 | 710.04 | 767.20 | 830.02 | 892.02 | 958.16 | 124.63 |
function [M1,s]=yd1(yt,n)
t=length(yt);
yt1=[];
for k=n:tyr=yt(k-n+1:k);yr1=mean(yr);yt1=[yt1,yr1];
end
M1=[zeros(1,n-1),yt1];
yt21=yt(n+1:t);
yt22=M1(n+1:t);
yts=yt22-yt21;
s=(sum(yts.^2)/(t-n))^0.5;
yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
n=5;
[m1,s1]=yd1(yt,3);
[m2,s2]=yd1(yt,4);
[m3,s3]=yd1(yt,5);
S=[0,s1,s2,s3];
Y=[yt;m1;m2;m3];
B=[Y,S'];
xlswrite('d:\yidong1.xlsx',B);
由表2可见,n=3比n=4预测效果好,n=4比n=5预测效果好。用n=3的计算作预测,12月份销售量为1027.23.
2.2 一次指数平滑预测法
(1)预测模型
设时间序列为y1,y2,…,yt,…,α为加权系数,0<α<1,一次指数平滑公式为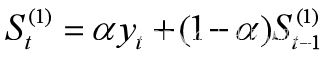
预测模型为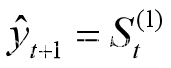
(2)加权系数的选择
(1)如果时间序列波动不大,比较平稳,则α取小一点,0.1-0.5,减小修正幅度,使预测模型包含较长的序列信息;
(2)如果序列具有迅速增加的变动趋势,α取大一点,0.6-0.8,使得预测模型灵敏度高一些,以便迅速跟上数据的变化。
(3)初始值的确定
一般选取最初几期实际值的平均值作为初始值。
案例2
就案例1中问题,用指数平滑预测法预测12月销售量。
就α=0.2,0.5,0.8分别作一次指数平滑预测,初始值为
即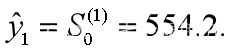
按照预测模型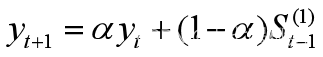 计算不同α预测结果与误差,计入表3,进行对比做出决策。
计算不同α预测结果与误差,计入表3,进行对比做出决策。
function [s1,s]=expph1(yt,a)
n=length(yt);
s1(1)=mean(yt(1:2));
for k=2:ns1(k)=a*yt(k)+(1-a)*s1(k-1);
end
y11=s1-yt;
s=std(y11);
yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
[m1,s1]=expph1(yt,0.2);
[m2,s2]=expph1(yt,0.5);
[m3,s3]=expph1(yt,0.8);
s=[0,s1,s2,s3];
m=[yt;m1;m2;m3];
B=[m,s'];
xlswrite('d:\yd1.xlsx',B);
表3 不同权系数的指数平滑预测及其标准误差
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| yt | 533.80 | 574.60 | 606.90 | 649.80 | 705.10 | 772.00 |
| a=0.2 | 554.20 | 558.28 | 568.00 | 584.36 | 608.51 | 641.21 |
| a=0.5 | 554.20 | 564.40 | 585.65 | 617.73 | 661.41 | 716.71 |
| a=0.8 | 554.20 | 570.52 | 599.62 | 639.76 | 692.03 | 756.01 |
| 月份 | 7 | 8 | 9 | 10 | 11 | 误差 |
| yt | 816.40 | 892.70 | 963.90 | 1015.10 | 1102.70 | 0.00 |
| a=0.2 | 676.25 | 719.54 | 768.41 | 817.75 | 874.74 | 81.82 |
| a=0.5 | 766.55 | 829.63 | 896.76 | 955.93 | 1029.32 | 28.33 |
| a=0.8 | 804.32 | 875.02 | 946.12 | 1001.30 | 1082.42 | 11.20 |
由表3可以看出,α=0.8误差最小,选择系数α=0.8进行预测,12月份的销售量为 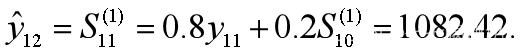
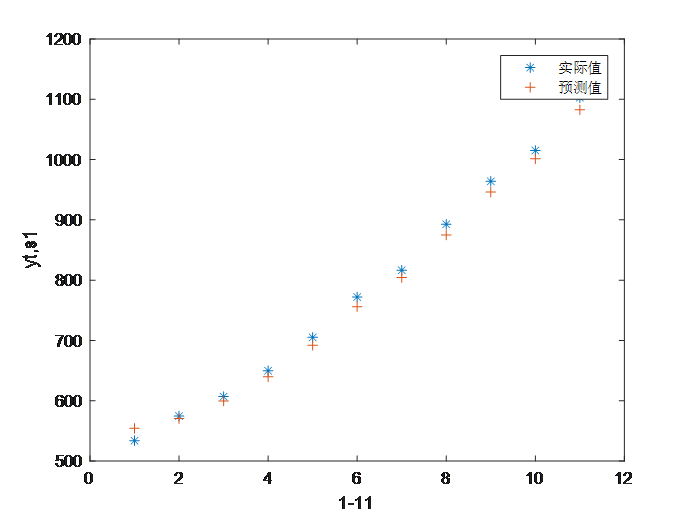
图2 预测值与实际值对比
从表2、表3和图2可以看出,预测值总是滞后于实际值。原因就是数据不满足模型要求(平稳型)。
3、差分指数平滑法
差分是改变数据趋势的根本方法(就像导数改变幂函数阶数一样)。如果数据呈现直线吻合型,差分后就呈现平稳性。
一阶差分指数平滑预测模型公式如下
 【1】
【1】
公式【1】的第三个表示是就相当于:预测值=原值+差分(微分)的预测值.
案例3
对案例1问题用差分指数平滑法预测第12月的销售量。(取α=0.5).
(1)先计算原始数据xt的差分,得到yt;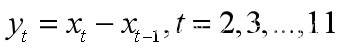
(2)对数据yt,取α=0.5做一次指数平滑预测,得到St;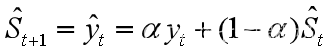
(3)作预测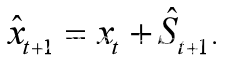
先编制一个给定时间序列和α的计算差分指数平滑预测的m函数,再调用m这个函数将计算结果汇总到表4.将预测结果与实测值对比如图3.差分指数平滑预测当α=0.5时,误差较小。
function [yc,err]=diffexpph(yt,a)
y=diff(yt);
[ym,s]=expph1(y,a);
y=[0,y];
ym=[0,ym];
n=length(y);
r=a*y(n)+(1-a)*ym(n);
ym=[ym,r];
for k=1:nyc(k+1)=ym(k+1)+yt(k);
end
xy=yc(2:end-1)-yt(2:end);
err=(sum(xy.^2)/10)^0.5;
yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7]; a=0.5;
[yc,err]=diffexpph(yt,a);plot(2:11,yt(2:end),'*',2:11,yc(2:end-1),'+'),
legend('实测值','预测值')
>> A1=[yt,0];
>> A=[A1;yc];
>> xlswrite('d:\diffexpph.xlsx',A)
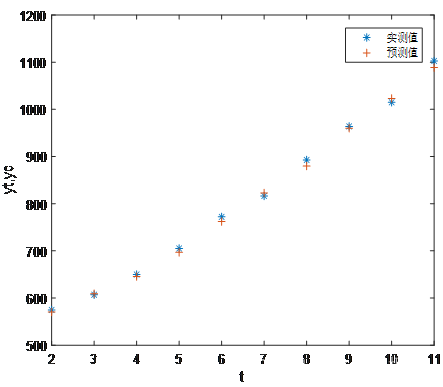
图3 差分指数平滑预测于实测对比
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 实测yt | 533.8 | 574.6 | 606.9 | 649.8 | 705.1 | 772 |
| 预测yc |
| 570.35 | 609.025 | 645.5625 | 696.7813 | 762.0406 |
| 月份 | 7 | 8 | 9 | 10 | 11 | 12 |
| 实测yt | 816.4 | 892.7 | 963.9 | 1015.1 | 1102.7 |
|
| 预测yc | 822.6703 | 879.8852 | 960.0426 | 1023.171 | 1088.536 | 1183.218 |
表4 案例3差分指数平滑预测有关数据
由表4可以得到预测值,第12月销售量为1183.218.将不同α取值(0.1,0.3,0.6,0.9)计算结果汇总到表5,对比显示,差分指数平滑对线性吻合型数据,α取值越大,预测越准确。
yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
[yc1,s1]=diffexpph(yt,0.1);
[yc2,s2]=diffexpph(yt,0.3);
[yc3,s3]=diffexpph(yt,0.6);
[yc4,s4]=diffexpph(yt,0.9);
A1=[0,yt(2:end),0];
A2=[0,s1,s2,s3,s4];
A=[A1;yc1;yc2;yc3;yc4]';
B=[A;A2];
xlswrite('d:\diffexpph1.xlsx',B)
| 月份\α |
| 0.1 | 0.3 | 0.6 | 0.9 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 574.6 | 570.35 | 570.35 | 570.35 | 570.35 |
| 3 | 606.9 | 610.725 | 609.875 | 608.6 | 607.325 |
| 4 | 649.8 | 643.7025 | 644.4625 | 646.24 | 648.7825 |
| 5 | 705.1 | 688.4523 | 692.6838 | 698.716 | 703.7583 |
| 6 | 772 | 746.577 | 755.1886 | 764.8064 | 770.7058 |
| 7 | 816.4 | 813.7693 | 820.382 | 822.5226 | 818.5206 |
| 8 | 892.7 | 861.6224 | 873.1574 | 882.389 | 889.7221 |
| 9 | 963.9 | 940.5202 | 953.7902 | 961.8156 | 964.1122 |
| 10 | 1015.1 | 1012.058 | 1022.023 | 1022.266 | 1017.121 |
| 11 | 1102.7 | 1067.202 | 1082.066 | 1091.006 | 1099.262 |
| 12 | 0 | 1158.352 | 1175.856 | 1185.623 | 1189.956 |
| 误差 | 0 | 19.44747 | 12.10722 | 6.799773 | 2.281841 |
表5 指数平滑不同α预测对比
4、具有季节性特点的时间序列的预测
具有季节特性的时间序列预测方法很多,这里介绍季节系数法,步骤如下:
(1)收集m年的每年各个季度或者各个月份(n个季度)的时间序列aij,i表示年份,i=1,2,…,m;j表示季度,j=1,2,…,n;
(2)计算所有数据的平均值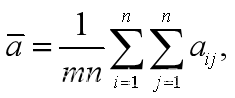
(3)计算同季度的算数平均数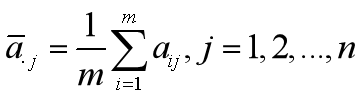
(4)计算季度系数
(5)预测计算
当时间序列是按季度给出,先求初预测年份(下一年)的年加权平均
再计算预测年份季度平均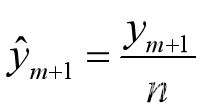
最后预测当年第j季度的预测值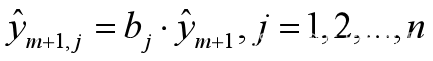
案例4
某商店某类商品1999-2000年各季度销售额如表6所示,预测2004年各季度销售额。
表6 1999-2003各季度销售额 (单位:元)
| 年份\季度 | 1 | 2 | 3 | 4 |
| 1999 | 137920 | 186742 | 274561 | 175422 |
| 2000 | 142814 | 198423 | 265419 | 183512 |
| 2001 | 131002 | 193987 | 247556 | 169847 |
| 2002 | 157436 | 200144 | 283002 | 194319 |
| 2003 | 149827 | 214301 | 276333 | 185204 |
| 2004 | 145573 | 201170 | 272696 | 183901 |
模型求解:按照上面的规范步骤,2004年个季度销售额预测填入表6最后一行
B=xlsread('d:\jidu.xlsx');
A=B(:,2:end);
[m,n]=size(A);
a=sum(sum(A))/m/n;
aj=mean(A);
bj=aj/a;
yi=sum(A');
w=1:m;
yc=sum(yi.*w)/sum(w)/n;
ycj=yc*bj相关文章:
数学建模——确定性时间序列分析方法
目录 介绍 确定性时间序列分析方法 1、时间序列的常见趋势 (1)长期趋势 (2)季节变动 (3)循环变动 (4)不规则变动 常见的时间序列模型有以下几类 2、时间序列预测的具体方法 …...

Opencv——颜色模型+通道分离与合并
视频加载/摄像头调用 VideoCapture允许一开始定义一个空的对象 VideoCapture video VideoCapture(const String &filename,int apiPreferenceCAP_ANY) filename:读取的视频文件或者图像序列名称 apiPreference:读取数据时设置的属性,例如编码格式、是否调用Op…...
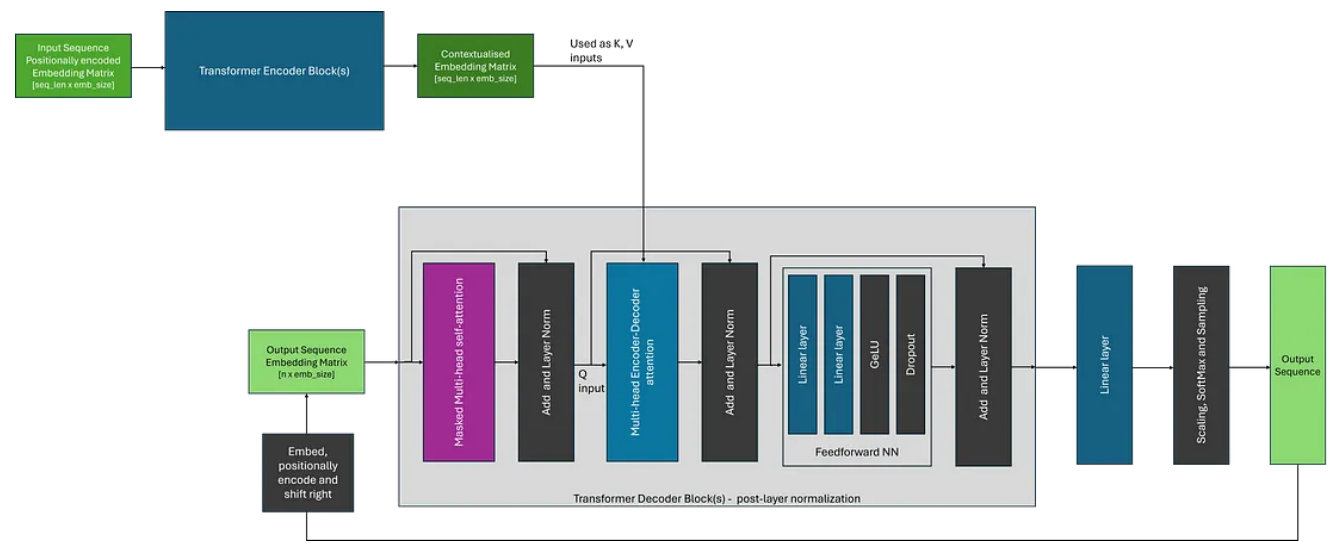
解码自然语言处理之 Transformers
自 2017 年推出以来,Transformer 已成为机器学习领域的一支重要力量,彻底改变了翻译和自动完成服务的功能。 最近,随着 OpenAI 的 ChatGPT、GPT-4 和 Meta 的 LLama 等大型语言模型的出现,Transformer 的受欢迎程度进一步飙升。这…...

【前端设计模式】之迭代器模式
迭代器模式是一种行为设计模式,它允许我们按照特定的方式遍历集合对象,而无需暴露其内部实现。在前端开发中,迭代器模式可以帮助我们更好地管理和操作数据集合。 迭代器模式特性 封装集合对象的内部结构,使其对外部透明。提供一…...
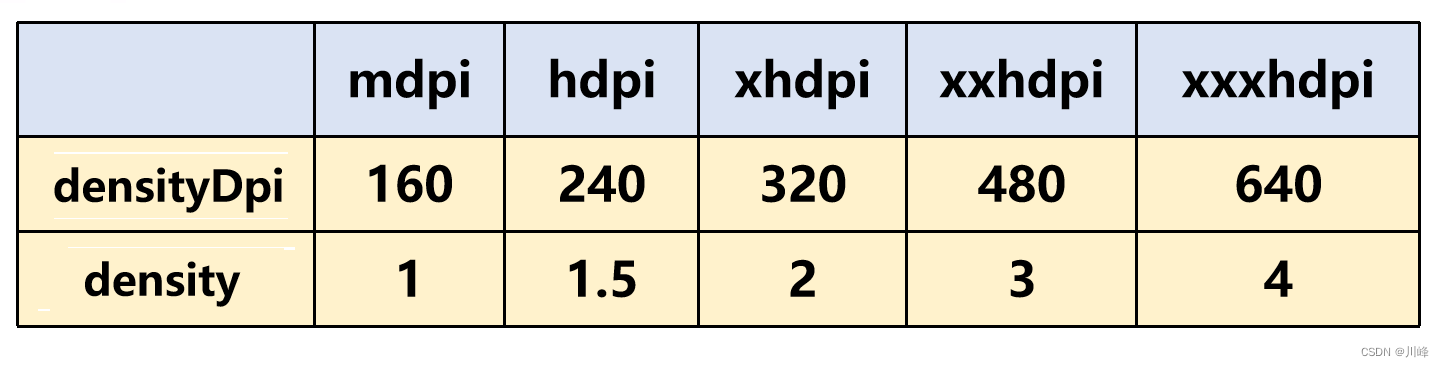
【Android知识笔记】图片专题(BitmapDrawable)
如何计算一张图片的占用内存大小? 注意是占用内存,不是文件大小可以运行时获取重要的是能直接掌握计算方法基础知识 Android 屏幕像素密度分类: (其实还有一种 ldpi = 120,不过这个已经绝种了,所以最低的只需关心mdpi即可) 上表中的比例为:m : h : xh : xxh: xxxh = …...
)
前端工程化知识系列(10)
目录 91. 了解前端工程化中的容器化和云部署概念,以及如何使用Docker和Kubernetes等工具来实现它们?92. 你如何管理前端项目的文档和知识共享,以确保团队成员都能理解和使用前端工程化工具和流程?93. 了解前端开发中的大规模和跨团…...
大数据flink篇之三-flink运行环境安装(一)单机Standalone安装
一、安装包下载地址 https://archive.apache.org/dist/flink/flink-1.15.0/ 二、安装配置流程 前提基础:Centos环境(建议7以上) 安装命令: 解压:tar -zxvf flink-xxxx.tar.gz 修改配置conf/flink-conf.yaml࿱…...

Redisson使用延时队列
延时队列 在开发中,有时需要使用延时队列。 比如,订单15分钟内未支付自动取消。 jdk延时队列 如果使用 jdk自带的延时队列,那么服务器挂了或者重启时,延时队列里的数据就会失效,可用性比较差。 Redisson延时队列 …...

基于php 进行每半小时钉钉预警
前言 业务场景:监控当前业务当出现并发情况时技术人员可以可以及时处理 使用技术栈: laravelredis 半小时触发一次报警信息实现思路 1、xshell脚本 具体参数就不详细解释了,想要详细了解可以自行百度 curl -H "Content-Type:appl…...
5.Python-使用XMLHttpRequest对象来发送Ajax请求
题记 使用XMLHttpRequest对象来发送Ajax请求,以下是一个简单的实例和操作过程。 安装flask模块 pip install flask 安装mysql.connector模块 pip install mysql-connector-python 编写app.py文件 app.py文件如下: from flask import Flask, reque…...

八皇后问题的解析与实现
问题描述 八皇后问题是一个古老而又著名的问题。 时间退回到1848年,国际西洋棋棋手马克斯贝瑟尔提出了这样的一个问题: 在88格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问一共有多少种摆法。 如何找到这所有的…...

论文浅尝 | 深度神经网络的模型压缩
笔记整理:闵德海,东南大学硕士,研究方向为知识图谱 链接:https://arxiv.org/abs/1412.6550 动机 提高神经网络的深度通常可以提高网络性能,但它也使基于梯度的训练更加困难,因为更深的网络往往更加强的非线…...

进阶JAVA篇- DateTimeFormatter 类与 Period 类、Duration类的常用API(八)
目录 1.0 DateTimeFormatter 类的说明 1.1 如何创建格式化器的对象呢? 1.2 DateTimeFormatter 类中的 format(LocalDateTime ldt) 实例方法 2.0 Period 类的说明 2.1 Period 类中的 between(localDate1,localDate2) 静态方法来创建对象。 3.…...
1.1 Windows驱动开发:配置驱动开发环境
在进行驱动开发之前,您需要先安装适当的开发环境和工具。首先,您需要安装Windows驱动开发工具包(WDK),这是一组驱动开发所需的工具、库、示例和文档。然后,您需要安装Visual Studio开发环境,以便…...

Jetpack:009-kotlin中的lambda、匿名函数和闭包
文章目录 1. 概念介绍2. 使用方法2.1 函数类型的变量2.2 高阶函数 3. 内容总结4.经验分享 我们在上一章回中介绍了Jetpack中Icon和Imamg相关的内容,本章回中主要介绍Kotlin中的 lambda、匿名函数和闭包。闲话休提,让我们一起Talk Android Jetpack吧&…...

openGauss指定schema下全部表结构备份与恢复
本次测试针对openGauss版本为2.0.5 gs_dump指定schema下全部表结构信息备份 gs_dump database_name -U username -p port -F c -s -n schema_name -f schema.sqldatabase_name:数据库名,要备份的数据库名称 username:用户名,数据…...

干货:如何在前端统计用户访问来源?
在前端统计用户访问来源是一个常见的需求,通过获取访问来源信息,我们可以了解用户是通过直接访问、搜索引擎、外部链接等途径进入我们的网站或应用。下面是一个详细的介绍,包括方法和实现步骤。 一、获取HTTP Referer HTTP Referer是HTTP请…...
李宏毅生成式AI课程笔记(持续更新
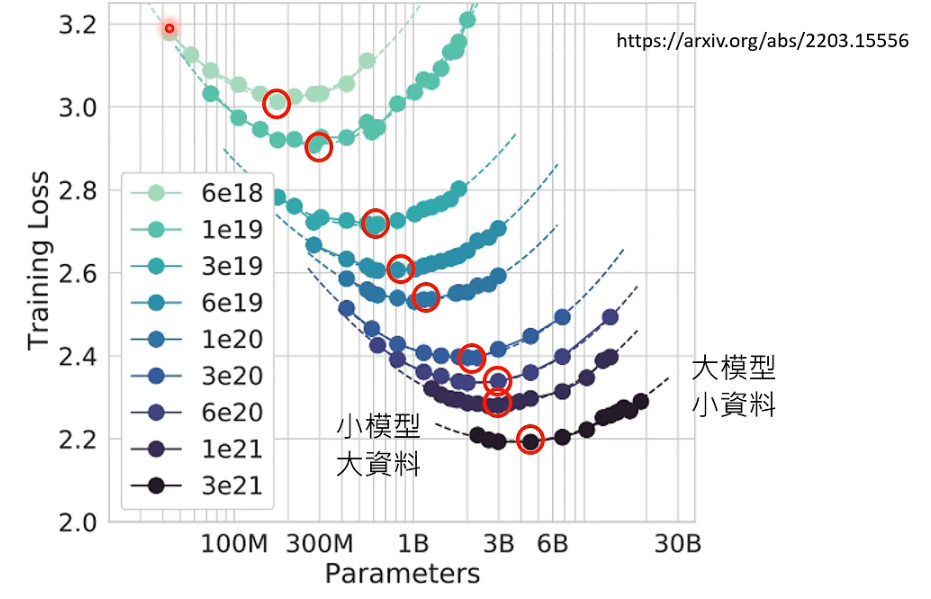
01 ChatGPT在做的事情 02 预训练(Pre-train) ChatGPT G-Generative P-Pre-trained T-Transformer GPT3 ----> InstructGPT(经过预训练的GPT3) 生成式学习的两种策略 我们在使用ChatGPT的时候会注意到,网站上…...
nodejs+vue+elementui酒店客房服务系统mysql带商家
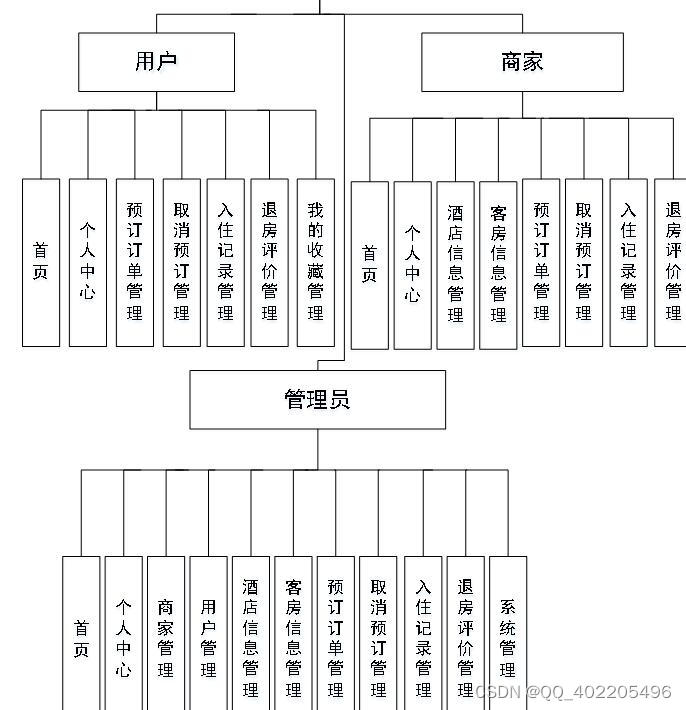
视图层其实质就是vue页面,通过编写vue页面从而展示在浏览器中,编写完成的vue页面要能够和控制器类进行交互,从而使得用户在点击网页进行操作时能够正常。 简单的说 Node.js 就是运行在服务端的 JavaScript。 前端技术:nodejsvueel…...
【网络协议】聊聊网络分层
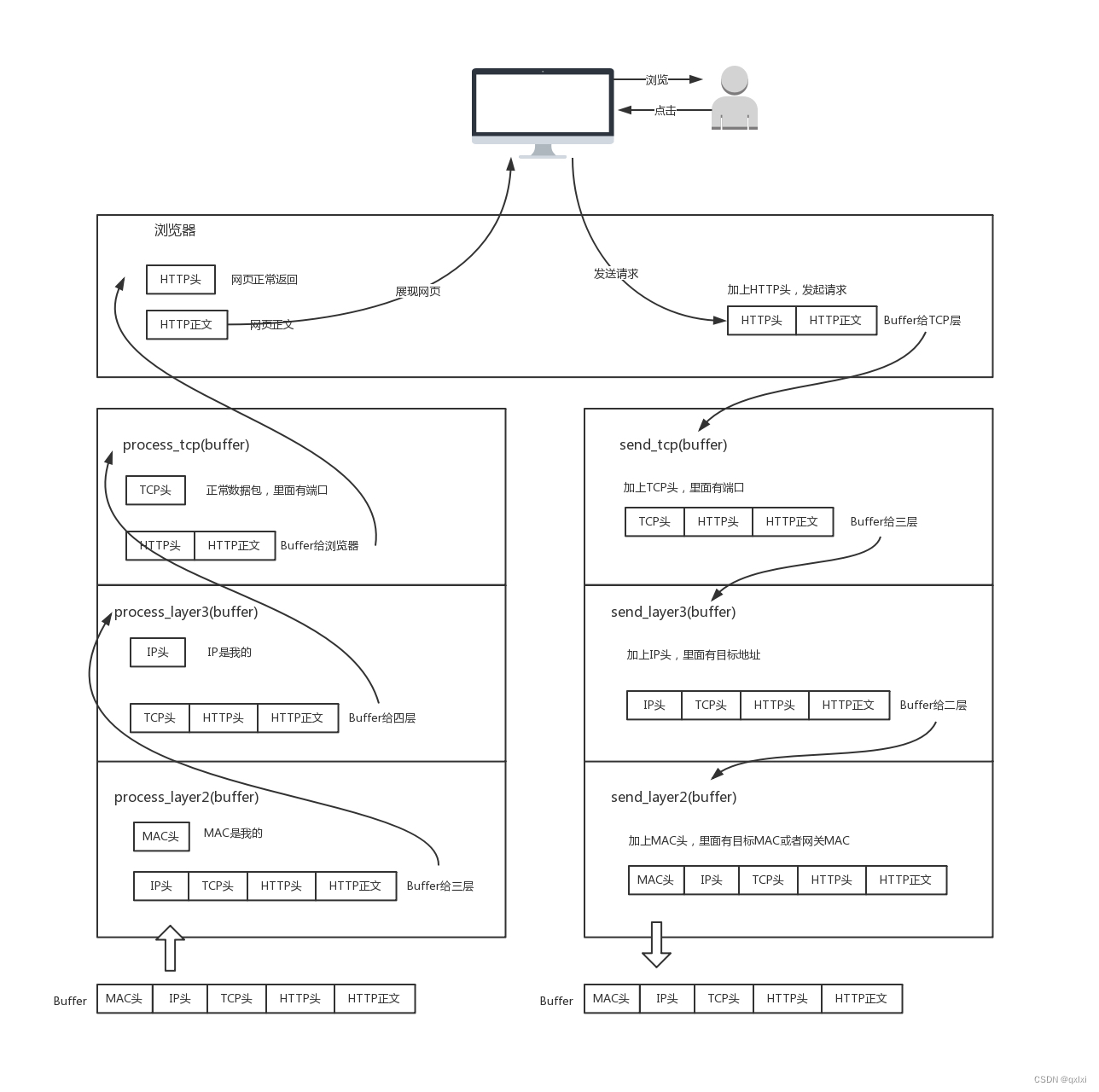
常用的网络协议 首先我们输入www.taobao.com,会先经过DNS进行域名解析,转换为59.82.122.115的公网IP地址。然后就会发起请求,一般来说非加密的使用http,加密的使用https。上面是在应用层做的处理,那么接下来就是到传输…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
