一致性公式证明
首先,假设存在两个不同的聚类假设 f 1 f^1 f1和 f 2 f^2 f2,它们在两个视角上的聚类结果分别为 y 1 ∈ { − 1 , + 1 } n y^1\in\{-1,+1\}^n y1∈{−1,+1}n和 y 2 ∈ { − 1 , + 1 } n y^2\in\{-1,+1\}^n y2∈{−1,+1}n。
证明一致性不等式:
P ( f 1 ≠ f 2 ) ≥ max { P e r r ( f 1 ) , P e r r ( f 2 ) } P(f^1\ne f^2)\ge\max\{P_{\mathrm{err}}(f^1), P_{\mathrm{err}}(f^2)\} P(f1=f2)≥max{Perr(f1),Perr(f2)}
其中 P e r r ( f ) P_{\mathrm{err}}(f) Perr(f)表示假设 f f f的误差概率,即:
P e r r ( f ) = E ( x , y ) ∼ D [ f ( x ) ≠ y ] P_{\mathrm{err}}(f)=\mathbb{E}_{(x,y)\sim D}[f(x)\ne y] Perr(f)=E(x,y)∼D[f(x)=y]
其中 ( x , y ) (x,y) (x,y)表示数据点和其标签, D D D表示数据的分布。假设我们从 D D D中采样 m m m个数据点 ( x 1 , y 1 ) , … , ( x m , y m ) (x_1,y_1),\ldots,(x_m,y_m) (x1,y1),…,(xm,ym),构成训练集 S = { ( x 1 , y 1 ) , … , ( x m , y m ) } S=\{(x_1,y_1),\ldots,(x_m,y_m)\} S={(x1,y1),…,(xm,ym)}。
使用训练集 S S S学习得到聚类假设 f S f_S fS,我们定义训练误差 P e r r ( f S ) P_{\mathrm{err}}(f_S) Perr(fS)为:
P e r r ( f S ) = 1 m ∑ i = 1 m 1 ( f S ( x i ) ≠ y i ) P_{\mathrm{err}}(f_S)=\frac{1}{m}\sum_{i=1}^m\mathbf{1}(f_S(x_i)\ne y_i) Perr(fS)=m1i=1∑m1(fS(xi)=yi)
其中 1 ( A ) \mathbf{1}(A) 1(A)表示当命题 A A A为真时取值为 1 1 1,否则取值为 0 0 0。
然后定义一个指示器函数 I ( S ) I(S) I(S)来判断训练误差是否落在某个区间之内。具体来说,对于给定的常数 δ ≥ 0 \delta\ge 0 δ≥0和 ϵ > 0 \epsilon>0 ϵ>0,我们定义:
I ( S ) = { 1 if P e r r ( f S ) − P e r r ( f ) > ϵ 0 otherwise I(S)=\begin{cases} 1&\text{if }P_{\mathrm{err}}(f_S)-P_{\mathrm{err}}(f)>\epsilon\\ 0&\text{otherwise} \end{cases} I(S)={10if Perr(fS)−Perr(f)>ϵotherwise
其中 f f f表示最优聚类假设,即:
f = a r g m i n g ∈ { − 1 , + 1 } n P e r r ( g ) f=\mathrm{argmin}_{g\in\{-1,+1\}^n}P_{\mathrm{err}}(g) f=argming∈{−1,+1}nPerr(g)
接下来,我们定义两个独立的随机变量序列 X 1 1 , X 2 1 , … , X n 1 X_1^1,X_2^1,\ldots,X_n^1 X11,X21,…,Xn1和 X 1 2 , X 2 2 , … , X n 2 X_1^2,X_2^2,\ldots,X_n^2 X12,X22,…,Xn2,它们分别表示假设 f 1 f^1 f1和 f 2 f^2 f2在两个视角上的聚类结果是否相同。
每个随机变量的取值为 0 0 0或 1 1 1,其中 1 1 1表示相同, 0 0 0表示不相同。
然后,定义:
X i j = { 1 if y i 1 = y i 2 0 otherwise X_i^j=\begin{cases} 1&\text{if }y_i^1=y_i^2\\ 0&\text{otherwise} \end{cases} Xij={10if yi1=yi2otherwise
利用Hoeffding不等式来估计随机变量 X i j X_i^j Xij的样本平均值与其期望之间的差异。根据Hoeffding不等式,对于任意 ϵ > 0 \epsilon>0 ϵ>0,有:
P ( ∣ 1 n ∑ i = 1 n X i j − E [ X i j ] ∣ > ϵ ) ≤ 2 exp ( − 2 n ϵ 2 ) P\left(\left|\frac{1}{n}\sum_{i=1}^nX_i^j-\mathbb{E}[X_i^j]\right|>\epsilon\right)\le 2\exp(-2n\epsilon^2) P( n1i=1∑nXij−E[Xij] >ϵ)≤2exp(−2nϵ2)
注意到 E [ X i j ] = P ( y i 1 = y i 2 ) \mathbb{E}[X_i^j]=P(y_i^1=y_i^2) E[Xij]=P(yi1=yi2),这个概率可以通过样本外估计得到。
事实上,假设从分布 D D D中采样 m m m个独立同分布的数据点 ( x 1 , y 1 ) , … , ( x m , y m ) (x_1,y_1),\ldots,(x_m,y_m) (x1,y1),…,(xm,ym)构成验证集 V = { ( x 1 , y 1 ) , … , ( x m , y m ) } V=\{(x_1,y_1),\ldots,(x_m,y_m)\} V={(x1,y1),…,(xm,ym)},则相同的概率可以估计为:
P ^ ( y i 1 = y i 2 ) = 1 m ∑ i = 1 m 1 ( y i 1 = y i 2 ) \hat{P}(y_i^1=y_i^2)=\frac{1}{m}\sum_{i=1}^m\mathbf{1}(y_i^1=y_i^2) P^(yi1=yi2)=m1i=1∑m1(yi1=yi2)
在估计 P ^ ( y i 1 = y i 2 ) \hat{P}(y_i^1=y_i^2) P^(yi1=yi2)时,通过将训练得到的聚类结果应用到验证集 V V V上来进行。
具体来说,对于每一个数据点 ( x i , y i ) ∈ V (x_i,y_i)\in V (xi,yi)∈V,我们选择 f 1 ( x i ) f^1(x_i) f1(xi)和 f 2 ( x i ) f^2(x_i) f2(xi)中相同的那一个作为其聚类结果,然后计算相同的数据点占比。
注意到由于是将训练得到的聚类结果应用到验证集上,因此估计出来的 P ^ ( y i 1 = y i 2 ) \hat{P}(y_i^1=y_i^2) P^(yi1=yi2)实际上是有偏的(即估计结果的期望不等于真实值),但是可以证明这个偏差是可以控制的。
不难发现,当 n n n充分大时,两个随机变量序列的样本平均值与其期望之间的差异会逐渐变小,即 ∣ 1 n ∑ i = 1 n X i j − E [ X i j ] ∣ \left|\frac{1}{n}\sum_{i=1}^nX_i^j-\mathbb{E}[X_i^j]\right| n1∑i=1nXij−E[Xij] 的概率收敛于 0 0 0。
同时,当训练误差与最优误差之差 Δ = P e r r ( f S ) − P e r r ( f ) \Delta=P_{\mathrm{err}}(f_S)-P_{\mathrm{err}}(f) Δ=Perr(fS)−Perr(f)大于 ϵ \epsilon ϵ时,指示器函数 I ( S ) I(S) I(S)的取值为 1 1 1,否则为 0 0 0。因此,我们可以将一致性不等式表示为:
P ( X − f 1 ≠ X − f 2 ) ≥ max { 1 2 exp ( − 2 n ϵ 2 ) − Δ , P e r r ( f 1 ) − P e r r ( f 2 ) − 2 ϵ } P(X-f^1\ne X-f^2)\ge\max\left\{\frac{1}{2}\exp(-2 n \epsilon^2)-\Delta, P_{\mathrm{err}}(f^1)-P_{\mathrm{err}}(f^2)-2\epsilon\right\} P(X−f1=X−f2)≥max{21exp(−2nϵ2)−Δ,Perr(f1)−Perr(f2)−2ϵ}
其中 Δ = P e r r ( f S ) − P e r r ( f ) \Delta=P_{\mathrm{err}}(f_S)-P_{\mathrm{err}}(f) Δ=Perr(fS)−Perr(f)表示训练误差与最优误差之差, ϵ \epsilon ϵ是控制误差幅度的常数。这个不等式就是我们想要证明的一致性不等式。
相关文章:

一致性公式证明
首先,假设存在两个不同的聚类假设 f 1 f^1 f1和 f 2 f^2 f2,它们在两个视角上的聚类结果分别为 y 1 ∈ { − 1 , 1 } n y^1\in\{-1,1\}^n y1∈{−1,1}n和 y 2 ∈ { − 1 , 1 } n y^2\in\{-1,1\}^n y2∈{−1,1}n。 证明一致性不等式: …...
allegro中shape的一些基本操作(一)——添加和修改shape
添加shape 简单添加shape的方式有3种,如下图所示 点击选择相应的shape模式后可以在option面板中设置相应的shape参数(这里不做过多介绍,里面可以设置shape的大小、静态或动态shape等参数),然后再用鼠标在相应的层上添…...
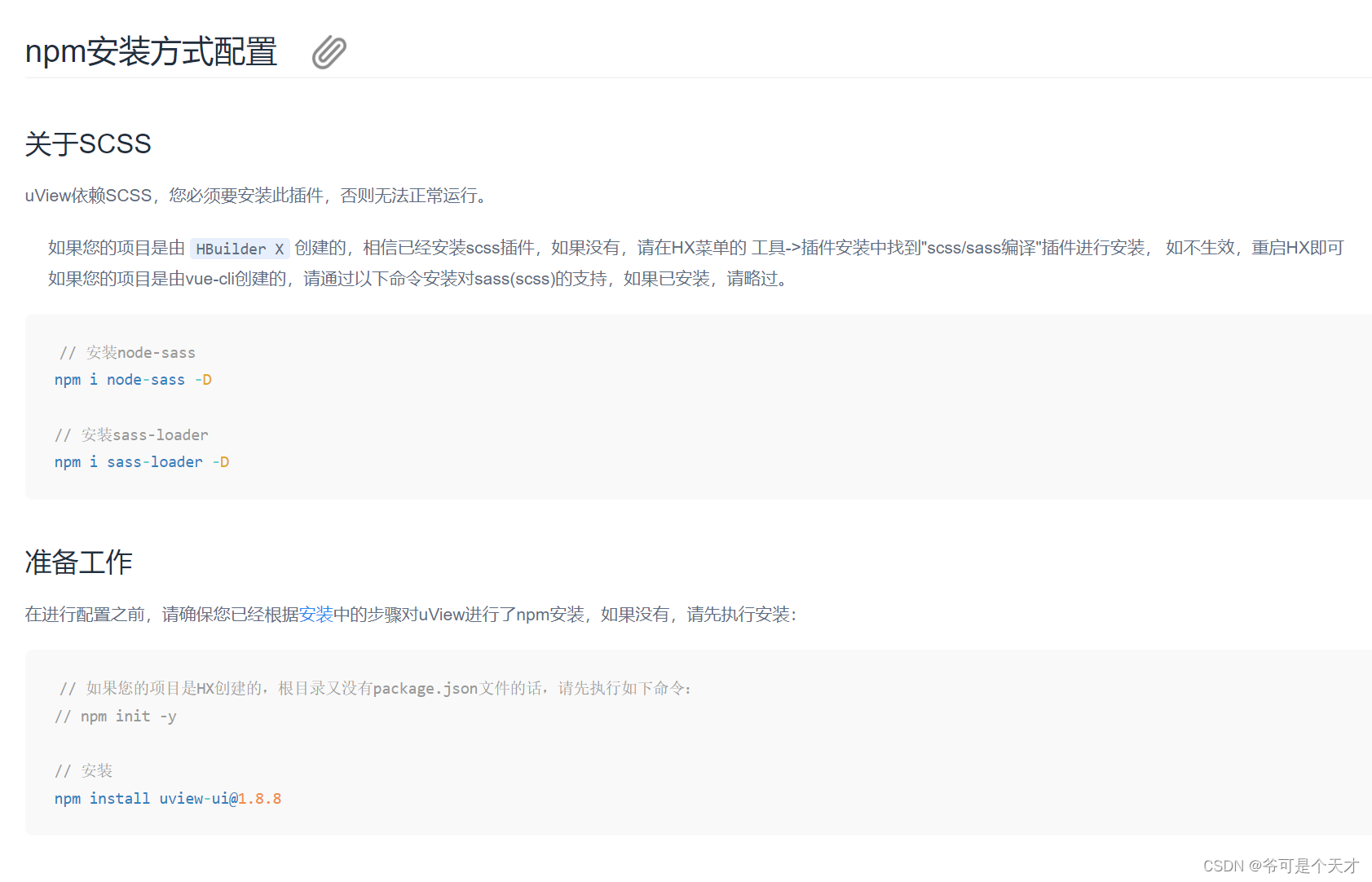
HBuilder创建uniapp默认项目导入uview(胎教)
1:更新HBuilder 建议更新 2:更新插件 我本人在没有更新插件的情况下报错了,找到了**这个大佬**解决问题,所以建议更新插件 先卸载uni-app(Vue2)编译 再重新安装 uni-app(Vue2)…...

C语言基础算法复习
003 斐波那契数列问题 #include<stdio.h> int main() {int i,f11,f21,f3,num;printf("%5d %5d",f1,f2);num2;for(i1; i<18; i){f3f1f2;f1f2;f2f3;num;printf("%5d",f3);if(num%40) printf("\n");}return 0; }//#输数斐波那契数列的前20…...
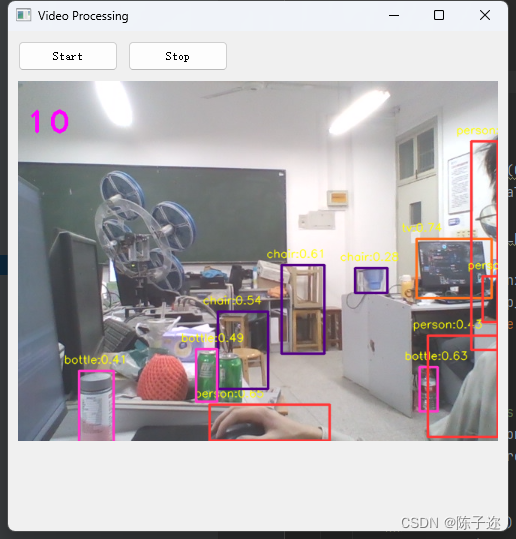
PyQt界面里如何加载本地视频以及调用摄像头实时检测(小白入门必看)
目录 1.PyQt介绍 2.代码实现 2.1实时调用摄像头 2.2 使用YOLOv5推理 2.3 代码中用到的主要函数 1.PyQt介绍 PyQt是一个用于创建桌面应用程序的Python绑定库,它基于Qt框架。Qt是一个跨平台的C应用程序开发框架,提供了丰富的图形界面、网络通信、数据…...
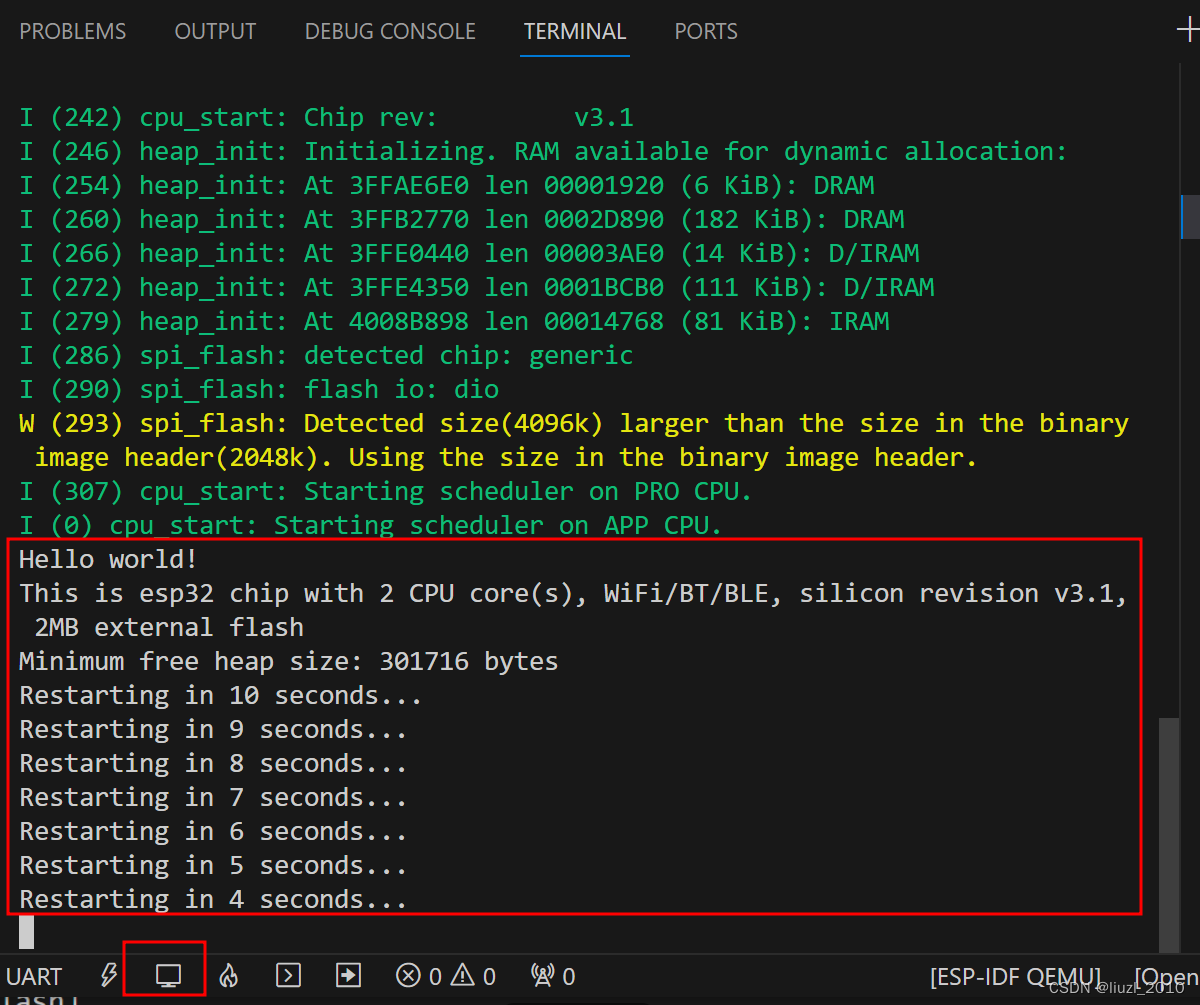
Ubuntu:VS Code IDE安装ESP-IDF【保姆级】
物联网开发学习笔记——目录索引 参考: VS Code官网:Visual Studio Code - Code Editing. Redefined 乐鑫官网:ESP-IDF 编程指南 - ESP32 VSCode ESP-ID Extension Install 一、前提条件 Visual Studio Code IDE安装ESP-IDF扩展&…...

软考高级系统架构设计师系列之:快速掌握软件工程核心知识点
软考高级系统架构设计师系列之:快速掌握软件工程核心知识点 一、软件开发方法二、软件开发模型三、软件开发模型-瀑布模型四、软件开发模型-经典模型汇总五、软件开发模型-增量模型与螺旋模型六、软件开发模型-V模型七、软件开发模型-构件组装模型八、软件开发模型-统一过程九…...

Java基础面试-ArrayList和LinkedList的区别
ArrayList: 基于动态数组,连续内存存储,适合下标访问(随机访问),扩容机制: 因为数组长度固定,超出长度存数据时需要新建数组,然后将老数组的数据拷贝到新数组,如果不是尾部插入数据还会涉及到元素的移动(往…...

如何从 Pod 内访问 Kubernetes 集群的 API
Kubernetes API 是您检查和管理集群操作的途径。您可以使用Kubectl CLI、工具(例如curl)或流行编程语言的官方集成库来使用 API 。 该 API 也可供集群内的应用程序使用。Kubernetes Pod 会自动获得对 API 的访问权限,并且可以使用提供的服务帐户进行身份验证。您可以通过使…...

计网面试复习自用
五层: 应用层:应用层是最高层,负责为用户提供网络服务和应用程序。在应用层,用户应用程序与网络进行交互,发送和接收数据。典型的应用层协议包括HTTP(用于网页浏览)、SMTP(用于电子邮…...
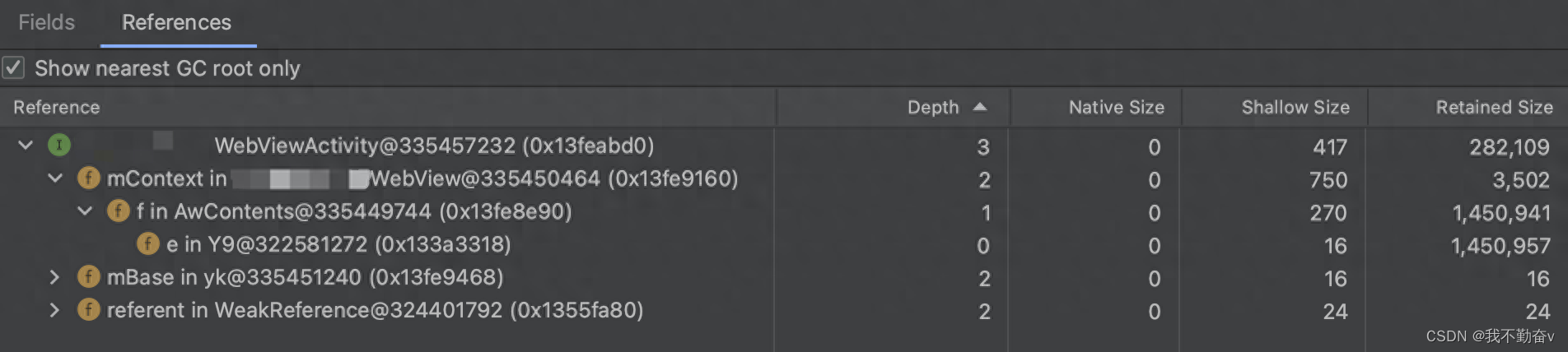
【Android 性能优化:内存篇】——WebView 内存泄露治理
背景:笔者在公司项目中优化内存泄露时发现WebView 相关的内存泄露问题非常经典,一个 Fragment 页面使用的 WebView 有多条泄露路径,故记录下。 Fragment、Activity 使用WebView不释放 项目中一个Fragment 使用 Webview,在 Fragm…...
C++入门(一)
文章目录 前言一、C的发展史二、c关键字二、c命名空间1、代码演示2、::(域作用限定符) 和namespace(命名空间)3、命名空间可以嵌套使用4、同一个工程中的相同名字的命名空间 三、c的输入&&输出1、iostream(输入…...

C#控制台程序读取输入按键非阻塞方式
参考内容: http://www.dutton.me.uk/2009-02-24/non-blocking-keyboard-input-in-c/ 相关代码: while (true) {if (Console.KeyAvailable){ConsoleKeyInfo key Console.ReadKey(true);switch (key.Key){case ConsoleKey.F1:Console.WriteLine("Y…...
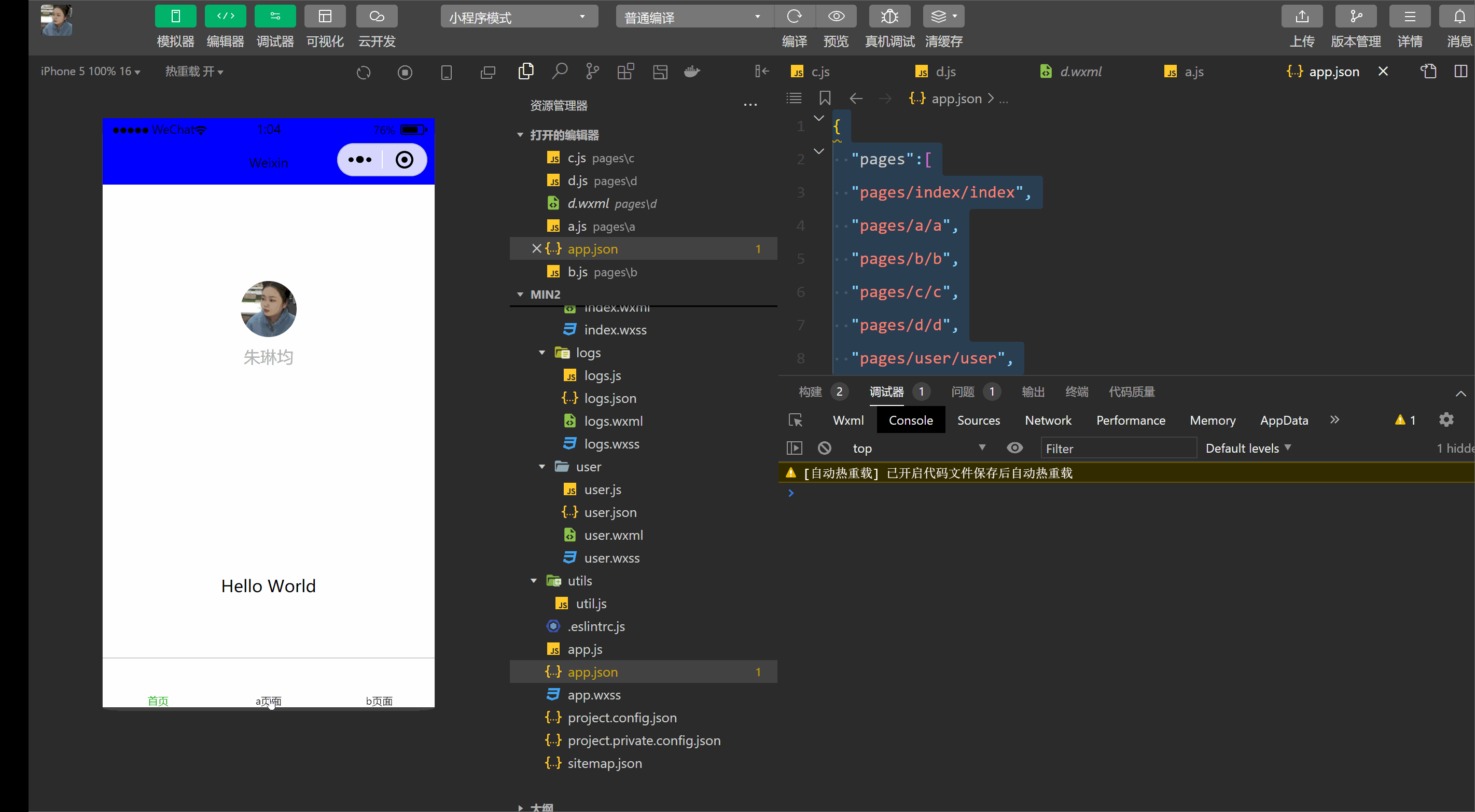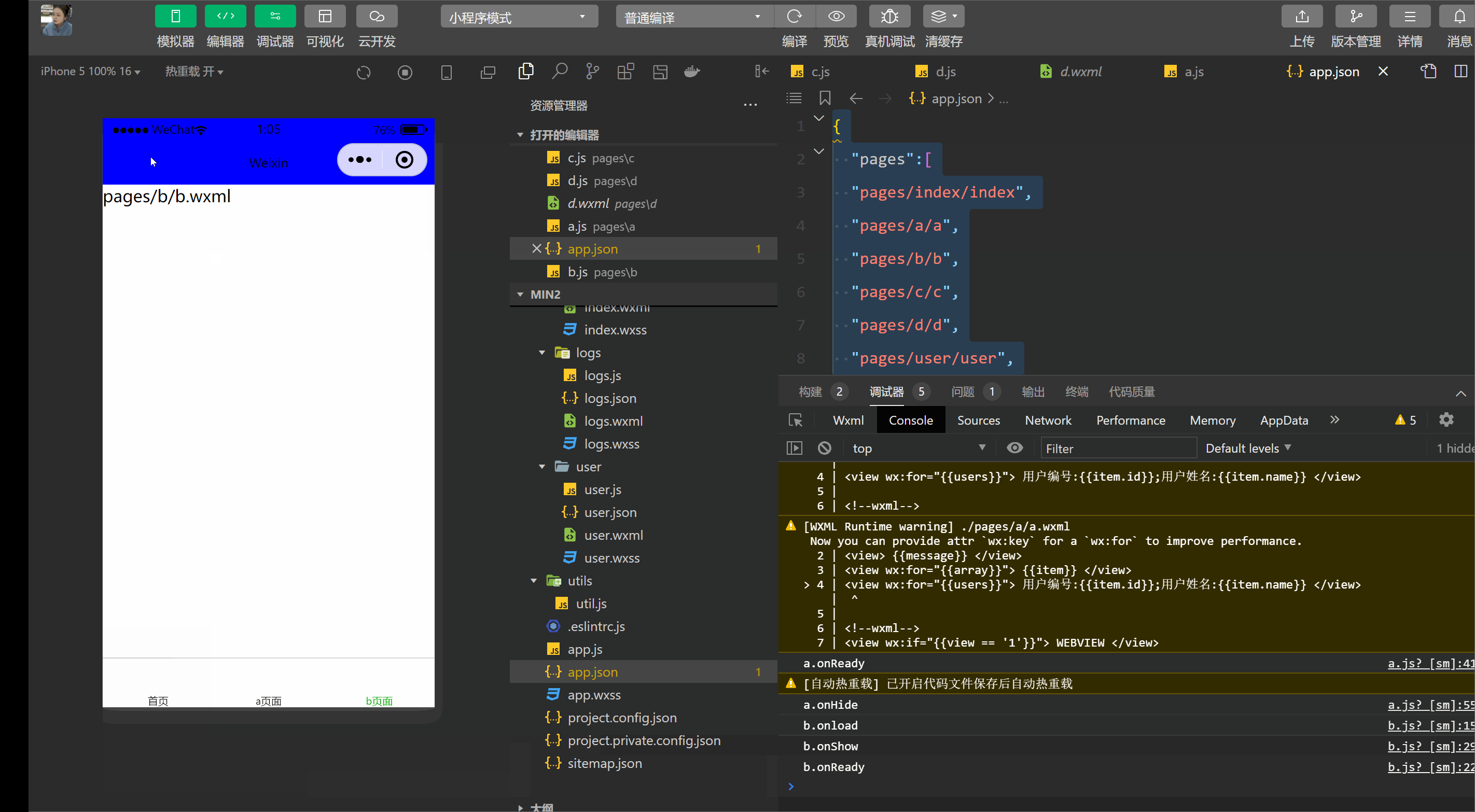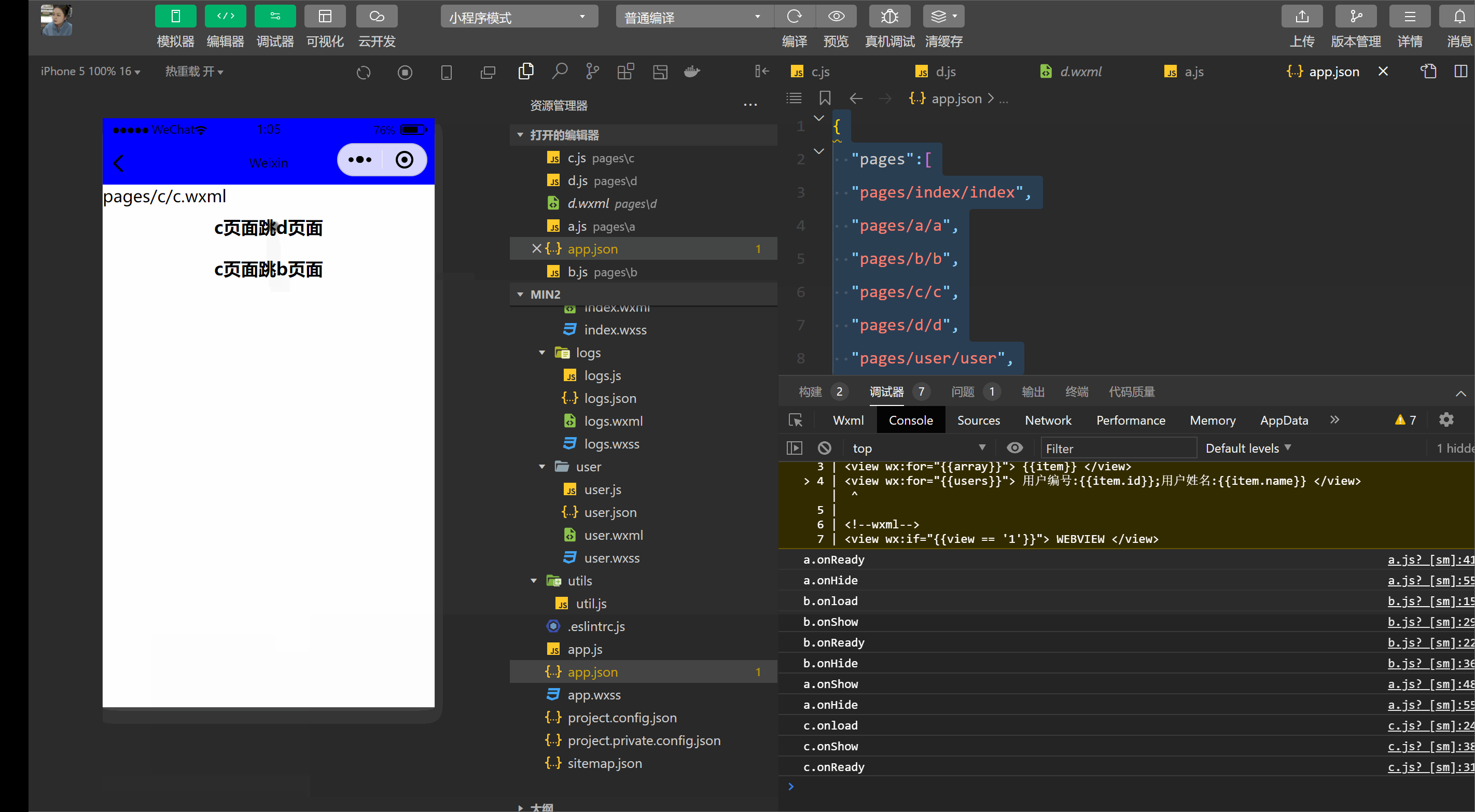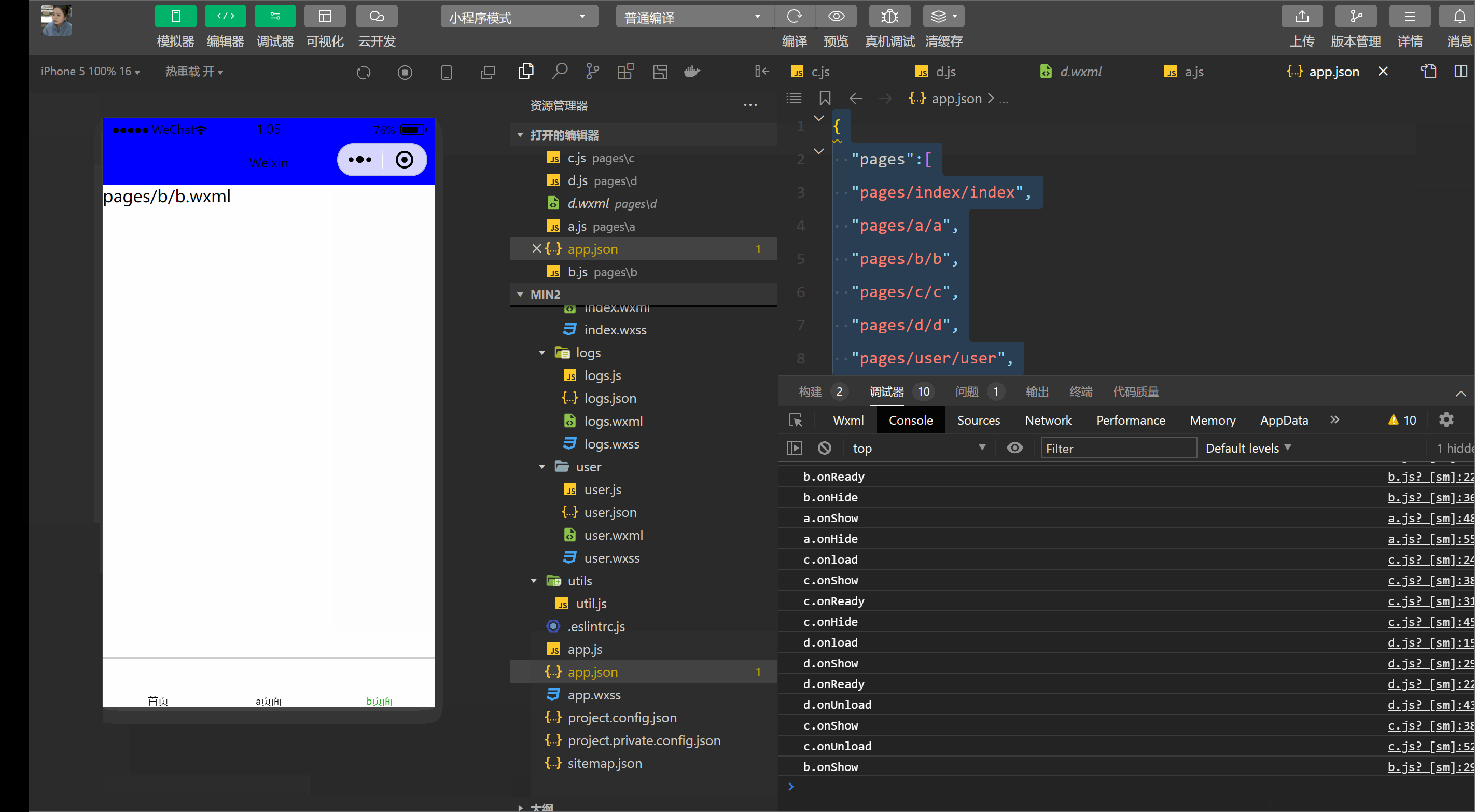
小程序框架->框架,视图层,生命周期(逻辑层)
框架视图层生命周期(逻辑层) 1.框架 小程序开发框架的目标是通过尽可能简单、高效的方式让开发者可以在微信中开发具有原生 APP 体验的服务。 整个小程序框架系统分为两部分:**[逻辑层](https://developers.weixin.qq.com/miniprogram/dev/framework/app-service/)…...
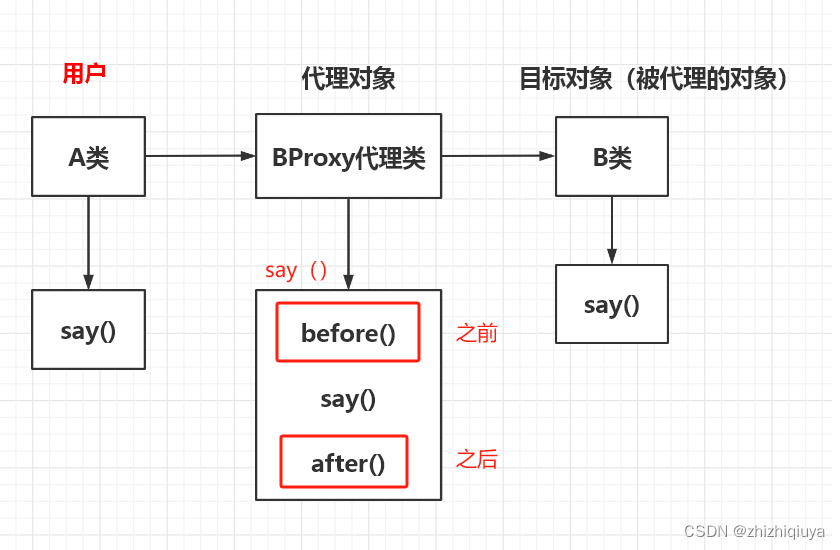
Spring framework Day14:配置类的Lite模式和Full模式
前言 Lite模式和Full模式是指在软件或系统中的不同配置选项。一般来说,Lite模式是指较为简洁、轻量级的配置,而Full模式则是指更加完整、功能更丰富的配置。 Lite模式通常会去除一些不常用或占用资源较多的功能,以提高系统的运行效率和响应…...

公司要做大数据可视化看板,除了EXCEL以外有没有好用的软件可以用
当企业需要进行大数据可视化看板的设计和开发时,除了Excel,还有许多其他强大且适合大数据可视化的软件工具。以下是几种常用的好用软件,以及它们的特点和优势,供您参考。 一、Datainside 特点和优势: - **易于使用**…...

掌握深入挖掘数据本质的方法
文章目录 掌握深入挖掘数据本质的方法1. 确定数据类型2. 数据清洗3. 数据可视化4. 探索性数据分析5. 特征工程6. 机器学习算法7. 自然语言处理 📕我是廖志伟,一名Java开发工程师、Java领域优质创作者、CSDN博客专家、51CTO专家博主、阿里云专家博主、清华…...
MyBatisPlus的学习项目页面
MyBatisPlus通过扫描实体类,并基于反射获取实体类信息作为数据库表信息 类名驼峰转下划线作为表名 名为id的字段作为主键 变量名驼峰转下划线作为表的字段名 常见注解 TableName:用来指定表名 Tableld:用来指定表中的主键字段信息 Tabl…...

基于EtherCAT的机器人多轴同步运动控制
随着工业自动化的发展,机器人在生产线上的应用越来越广泛。为了实现高效、精确的运动控制,机器人的多轴运动必须能够实现同步操作,它能够提高机器人的运动精度和稳定性,实现更高效的生产线操作。同时,它也为机器人的协…...
彩虹易支付 9.27 最新版加订单查询 sy 更新版
彩虹易支付 9.27 最新版加订单查询 sy 更新版 修复客服 2023/09/25: 1. 新增支付宝红包支付插件 2. 新增支付宝 APP 支付转 H5 支付 3. 更新了几个支付插件 安装教程: 环境:php7.2 上传后访问域名进行安装即可 源码下载:ht…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
