随机误差理论与测量
文章目录
- 第1节 随机误差的性质和特点
- 第2节 随机误差的数字特性
- 标准差的估计
- 第3节 单次测量结果的精度指标
- 第4节 多次测量结果的精度指标
- 算数平均值的分布特性与标准差
- 算数平均值的置信度
- 算数平均值的精度指标(常用的有4个)
- 第5节 非等精度测量
第1节 随机误差的性质和特点
随机误差的基本特点:对称性、单峰性、抵偿性、有界性。
随机误差的分布特性:古典误差理论认为:随机误差服从正态分布。其理论依据:中心极限定理。
正态分布及特性:


查分布表时用半边值
第2节 随机误差的数字特性
随机变量的数字特征:
数学期望体现位置特征,方差体现分散性指标。
算术平均值(数学期望的估计)
可以用算数平均值作为真值的估计。
解决了有限次等精度测量中,如何估计被测量真值的问题。

Dx为方差。
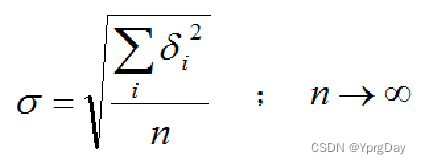
这里的 δ \delta δ 是误差(测量值-真值),而真值是无法得到的,所以要进行标准差的估计方法。
标准差的估计
贝赛尔公式
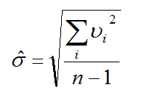
注意这里的 σ \sigma σ是带了帽子的。戴帽子的 σ \sigma σ是不带的无偏估计。
Vi表示的是残差(测量值-平均值),所以是可以得到的。
贝赛尔公式估算条件:测量次数n比较大。
标准偏差的其他估算方法
1)别捷尔斯法(Peters)

2)极差法

dn可查表得到,与测量次数有关(测量n次就查dn):测量的次数越多,ωn大的概率高,故dn应大。极差法可简单迅速算出标准差,n<10时适用。
3) 最大误差法

四种估计方法的优缺点对比
① 贝塞尔公式的计算精度较高,但计算麻烦,需要乘方和开方等,其计算速度难于满足快速自动化测量的需要;
② 别捷尔斯公式最早用于前苏联列宁格勒附近的普尔科夫天文台,它的计算速度较快,但计算精度较低,计算误差为贝氏公式的1.07倍;
③ 用极差法计算σ,非常迅速方便,可用来作为校对公式,当n<10时可用来计算σ,此时计算精度高于贝氏公式;
④ 用最大误差法计算σ更为简捷,容易掌握,当n<10时可用最大误差法,计算精度大多高于贝氏公式,尤其是对于破坏性实验(n=1)只能应用最大误差法。
第3节 单次测量结果的精度指标
正态分布的概率积分——误差函数
标准差σ是表征随机误差很重要的一个特征量,可用于描述测量列中各个测得值的误差。
σs可作为表征测量列中每一个测得值误差的参数。
单次测量是总体中的一次抽样,目前各国多采用以下精度指标:
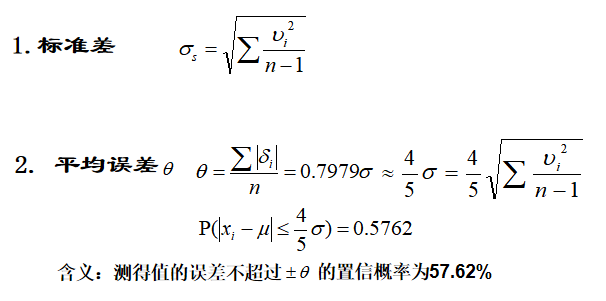

在一个测量列中,是以算术平均值作为测量结果:

因此必须研究算术平均值不可靠的评定标准!
第4节 多次测量结果的精度指标
算数平均值的分布特性与标准差
用 x ‾ \overline{x} x 作为测量结果比用单次测量结果精度提高了 n \sqrt{n} n倍!


算数平均值的置信度
测量次数多时,查正态分布表
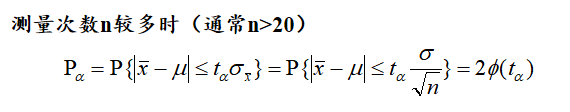

测量次数n较少时——t分布求解

当自由度趋向于无穷大时,t分布就是标准的正态分布。实际上在测量次数足够大(n>20),可以近似用正态分布代替。

其中自由度V=n-1=4,a=0.05。
t分布在数理统计中称为小子样分布。在精密测量中,测量次数很少有超过20次的,因此,在理论上应按t分布来计算相应的误差限;只有在测量次数较多(n>20)的情况时,或其测量量不甚重要时,才可近似应用正态分布的理论来处理。
事实上,当n无限增大时,t分布曲线和正态分布曲线基本重合,即按两个分布理论来处理测量数据,所得的结果差异是极小的。
算数平均值的精度指标(常用的有4个)

第5节 非等精度测量
什么是非等精度测量
测量条件(人员、方法、测量次数、环境条件等)部分或者全部改变,导致测量的精度和可信赖程度不一样。这种测量称为非等精度测量。
客观上,由于条件限制,所有的测量都是非等精度测量。但是条件差别不大的测量,一般都当成等精度处理。
等精度测量特点:具有同一标准差 σ \sigma σ。
非等精度测量的两种情况
(1)用不同的测量次数进行对比测量
(2)用不同精度的仪器进行对比测量:互比核对目的。
“权”的概念和加权平均
权与方差的关系
方差越大,测量结果越不可靠,权应该越小。
权与方差成反比!权表示相对可靠程度,是一个无量纲的数,允许给各组的权数同时增大或者减小若干倍,而比例关系不变。
相关文章:

随机误差理论与测量
文章目录 第1节 随机误差的性质和特点第2节 随机误差的数字特性标准差的估计 第3节 单次测量结果的精度指标第4节 多次测量结果的精度指标算数平均值的分布特性与标准差算数平均值的置信度算数平均值的精度指标(常用的有4个) 第5节 非等精度测量 第1节 随机误差的性…...
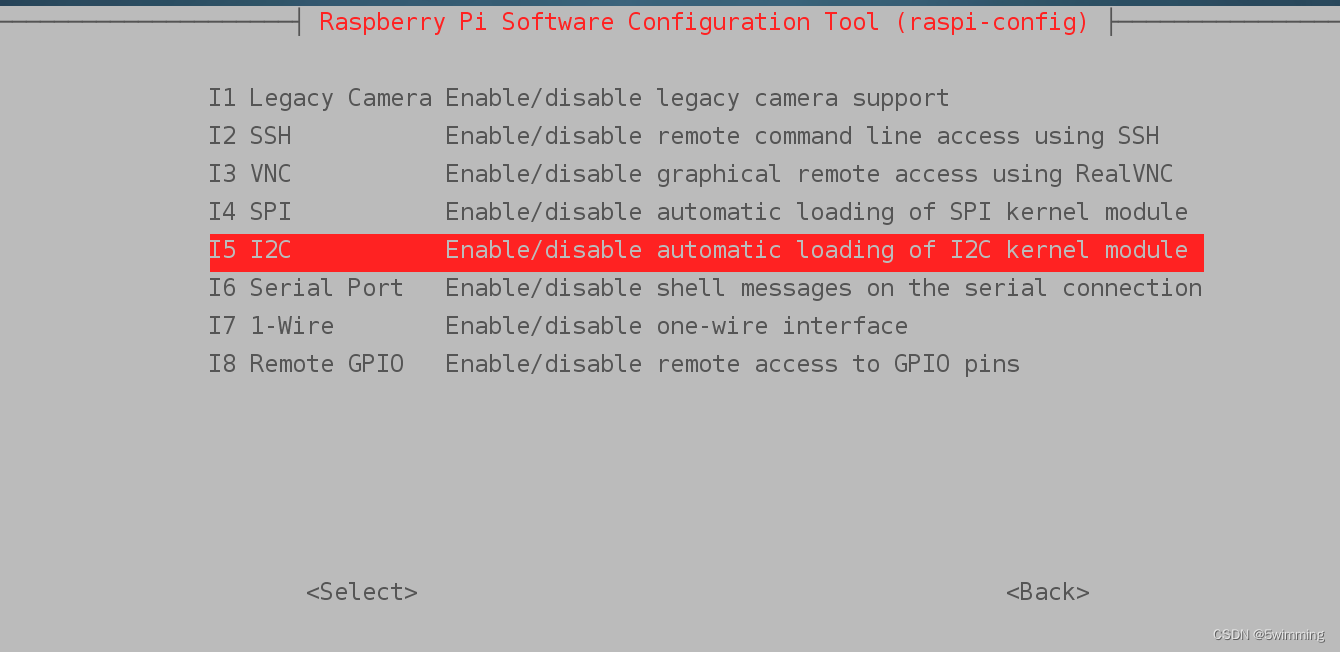
树莓派4b配置通过smbus2使用LCD灯
出现报错: FileNotFoundError: [Errno 2] No such file or directory: ‘/dev/i2c-1’ 则说明没有打开I2C,可通过如下步骤进行设置 1、打开树莓派配置 sudo raspi-config2、进入Interface Options,配置I2C允许 目前很多python3版本已经不…...

UPS 原理和故障案例分享
摘要:不间断电源UPS (Uninterruptible Power System),主要是由整流器、 逆变器、静态旁路和储能装置等组成;具备高可靠性、高可用性和高质量的独立 电源。通过对收集的 UPS 故障案例进行分析,从施工,调试和运行三个方面筛选 出四个故障案例与…...

Stream流中的 max()和 sorted()方法
需求:某个公司的开发部门,分为开发 一部 和 二部 ,现在需要进行年中数据结算。分析: 员工信息至少包含了(名称、性别、工资、奖金、处罚记录)开发一部有 4 个员工、开发二部有 5 名员工分别筛选出 2 个部门…...
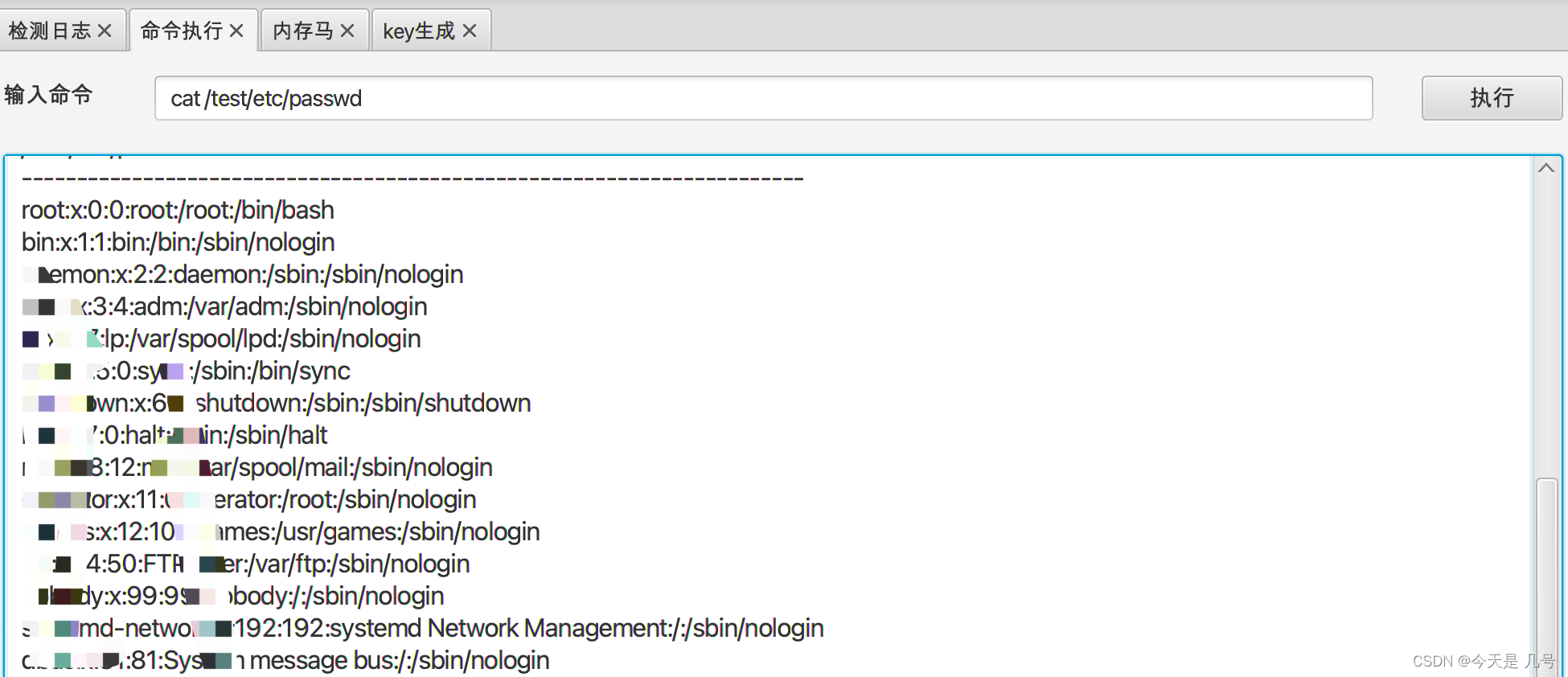
云上攻防-云原生篇Docker安全权限环境检测容器逃逸特权模式危险挂载
文章目录 前言1、Docker是干嘛的?2、Docker对于渗透测试影响?3、Docker渗透测试点有那些?4、前渗透-判断在Docker中方式一:查询cgroup信息方式二:检查/.dockerenv文件方式三:检查mount信息方式四࿱…...

PDE数值解中,为什么要引入弱解(weak solution)的概念?
See https://www.zhihu.com/question/24243246?utm_sourceqq&utm_mediumsocial&utm_oi1315073218793488384...

使用pdfjs实现在线预览pdf
在工作中可能会遇到前端展示pdf文件进行预览并提供下载的需求场景,例如操作指引,这个时候需要寻找一款实现该功能的插件,以pdjjs举例子 1. 安装pdf.js npm install pdfjs-dist2. 引入pdf.js import pdfjsLib from pdfjs-dist3.加载pdf文件流 这个地方区分是请求后端接口还是…...
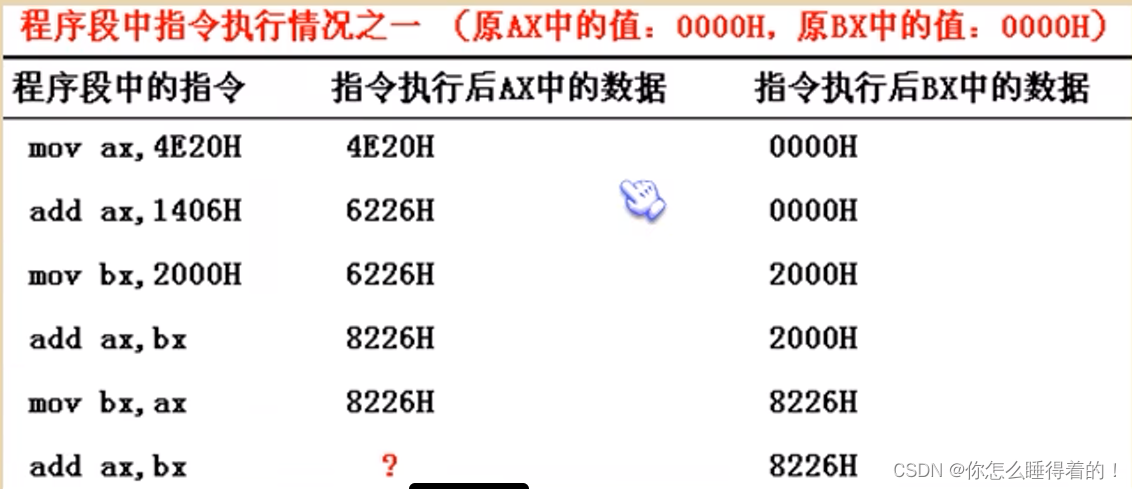
汇编语言基础
引言 汇编语言是直接在硬件之上工作的编程语言,首先要了解硬件系统的结构,才能有效的应用汇编语言对其编程。汇编课程的研究重点放在如何利用硬件系统的编程结构和指令集有效灵活的控制系统进行工作。 基础知识 1.1机器语言 机器语言是机器指令的集合…...
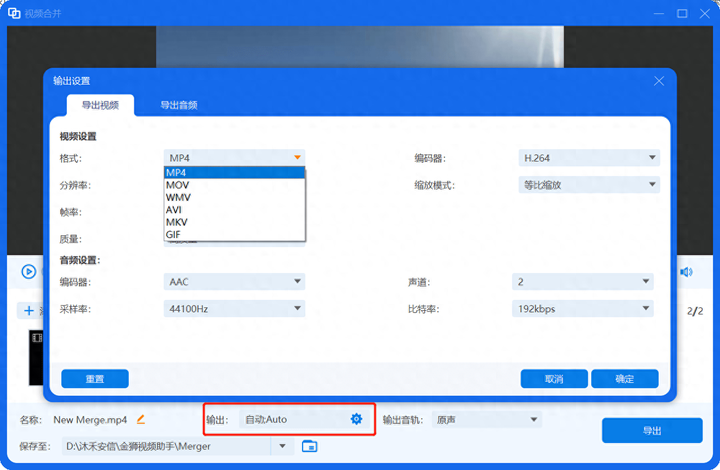
格式工厂怎么把两个视频合并在一起
免费的工具谁不喜欢呢,今天为大家介绍的是格式工厂这款多功能视频转换软件,然而今天主要为大家介绍的是格式工厂的视频合并功能。 是的,你没有听错,格式工厂除了转换之外,还可以视频合适、视频剪辑、视频分割、去水印…...
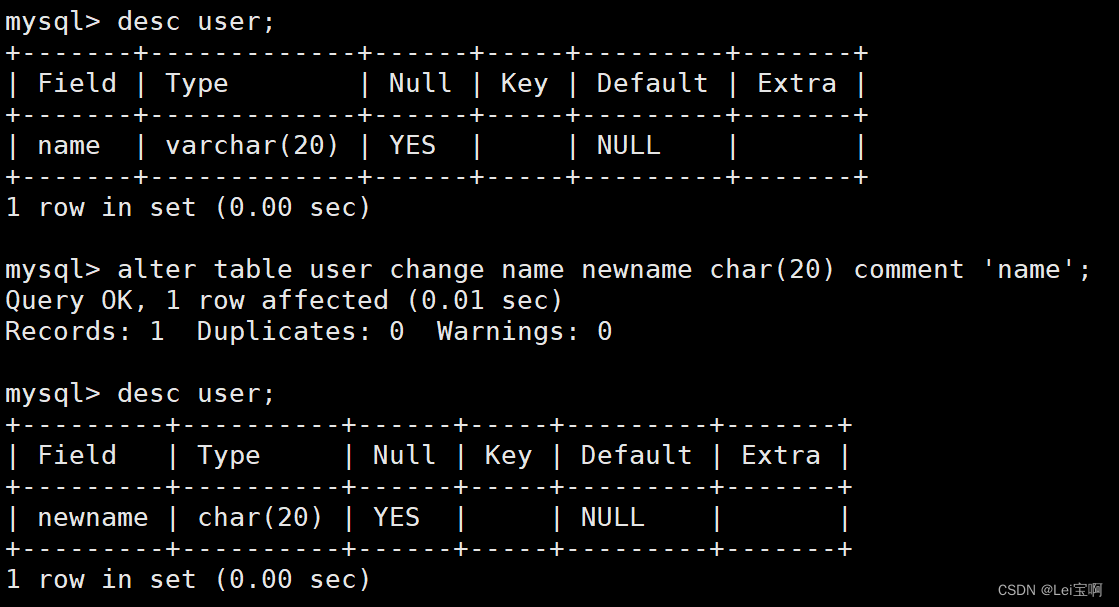
2.MySQL表的操作
个人主页:Lei宝啊 愿所有美好如期而遇 表的操作 (1)表的创建 CREATE TABLE table_name ( field1 datatype, field2 datatype, field3 datatype ) character set 字符集 collate 校验规则 engine 存储引擎; 存储引擎的不同会导致创建表的文件不同。 换个引擎。 t…...

网络安全之应急流程
近期需要弄一个网络安全应急的流程,其实对于网络安全应急并不陌生,只是在一些特定的环境上会遇到一些难以解决的问题或者缺少某个岗位的技术人员,因为不同运营商的应急小队也是不同的岗位,如今有着安全设备的告警和预警࿰…...

[Python进阶] 操纵鼠标:pyuserinput
6.2 操纵鼠标:pyuserinput 6.2.1 说明 在安装pyuserinput库时会自动安装PyMouse和PyKeyboard库。前者主要用来操作鼠标,包括鼠标的点击、移动等。后者主要用来操作键盘,包括键盘按键的按下、弹起等。 这两个库还可以同时对鼠标和键盘的事件…...
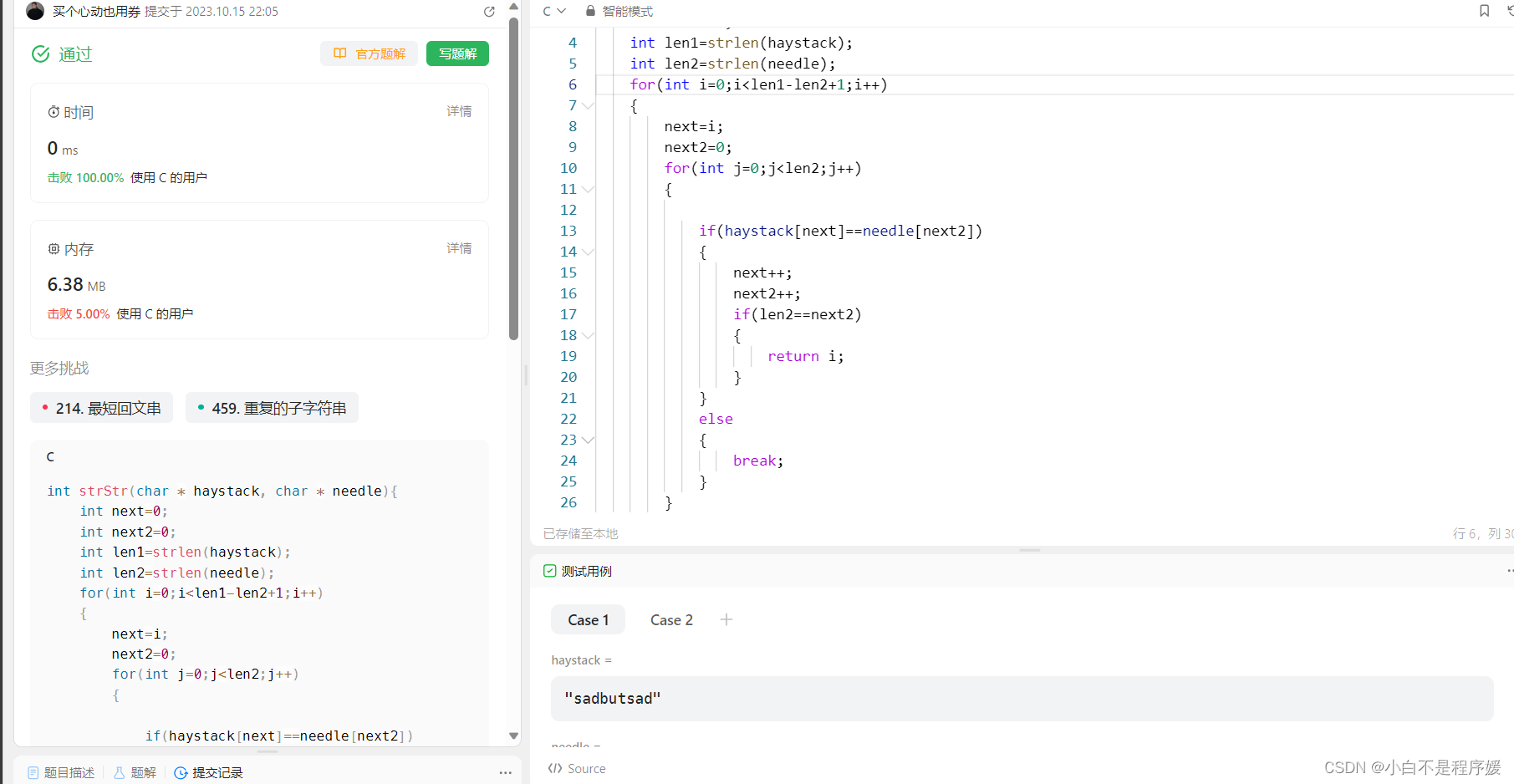
【LeetCode】每日一题两数之和寻找正序数组的中位数找出字符串中第一个匹配项的下标在排序数组中查找元素的第一个和最后一个位置
主页点击直达:个人主页 我的小仓库:代码仓库 C语言偷着笑:C语言专栏 数据结构挨打小记:初阶数据结构专栏 Linux被操作记:Linux专栏 LeetCode刷题掉发记:LeetCode刷题 算法:算法专栏 C头…...
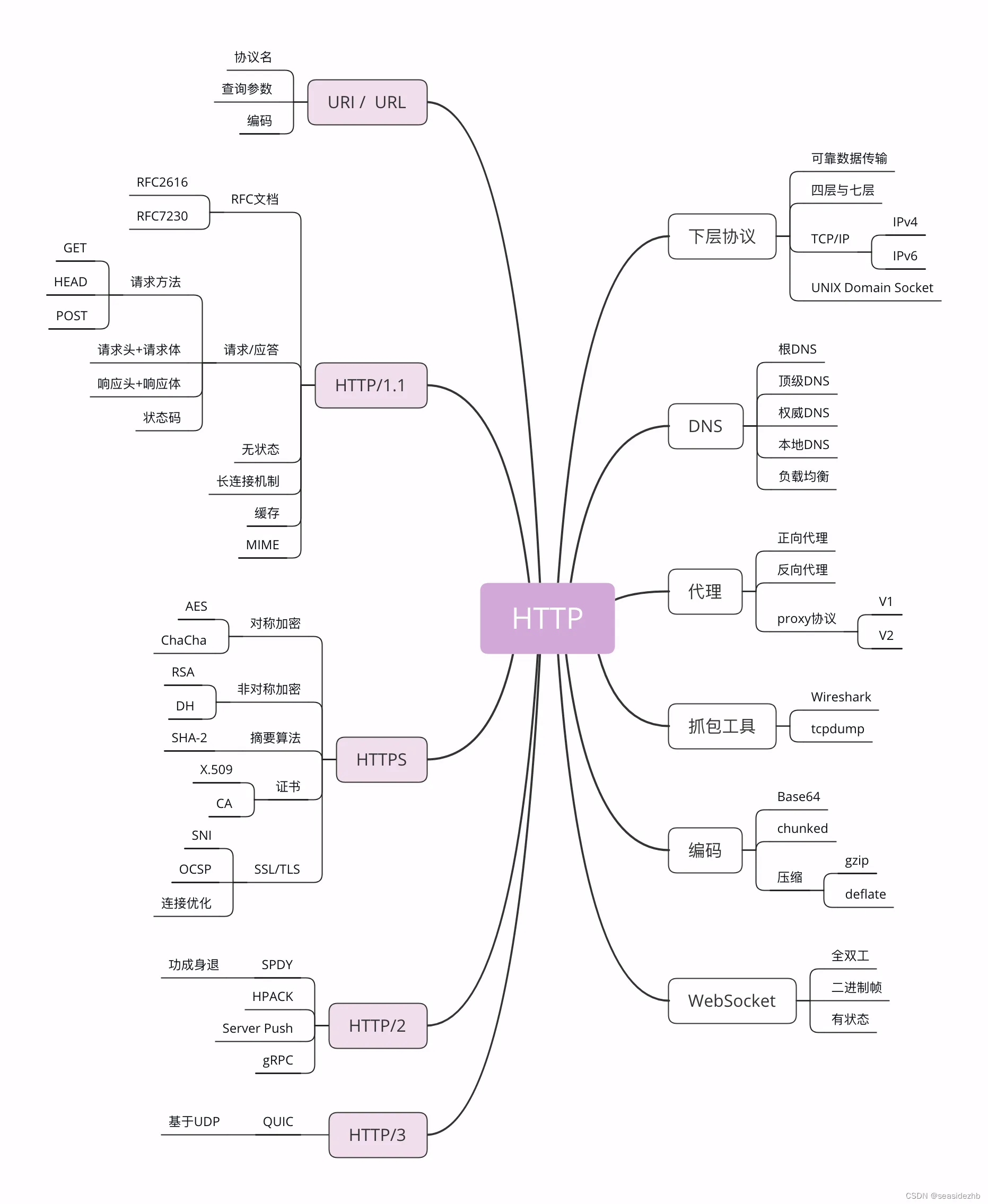
与HTTP相关的各种协议
TCP/IP TCP/IP协议是目前网络世界“事实上”的标准通信协议,实际上是一系列网络通信协议的统称,其中最核心的两个协议是 TCP和IP,其他的还有 UDP、ICMP、ARP 等等,共同构成了一个复杂但有层次的协议栈。 这个协议栈有四层&#x…...

常见的网络攻击手段
网络攻击对个人、组织和整个社会都带来了严重的威胁,因此必须采取有效的安全措施来保护网络系统和用户的信息安全。网站是攻击者经常瞄准的目标,以下是一些常见的攻击方式: 1. DDoS攻击(分布式拒绝服务攻击)࿱…...

学习笔记---超基础+详细+新手的顺序表~~
目录 1.顺序表的前言 1.1 顺序表--->通讯录📇 1.2 数据结构的相关概念🏇 1.2.1 什么是数据结构 1.2.1 为什么需要数据结构 2. 顺序表概念及分类 2.1 顺序表的概念🐙 2.2 顺序表的分类🐫 2.2.1 顺序表和数组的区别 2.…...

Java高级-CompletableFuture并发编程利器
CompletableFuture核心Api 1.概述2.Async2.a) supplyAsync2.b) runAsync 3.Then3.a) thenApply()3.b) thenApplyAsync() 1.概述 Future可以在并发编程中异步获取结果 CompletableFuture实现了Future接口,肯定也会有Future的功能,也相当于是Future的一个…...

python、java、c++哪一个前景比较好?
Python是一种广泛使用的高级编程语言,适用于数据分析、人工智能、机器学习等领域。Java是一种通用的编程语言,适用于企业级应用开发、网站开发、软件开发、嵌入式领域等。C是一种系统编程语言,适用于嵌入式开发、游戏开发、音视频、服务端开发…...

【排序算法】详解直接插入排序和希尔排序原理及其性能分析
文章目录 插入排序算法原理细节分析代码实现复杂度分析:稳定性分析:与冒泡排序的对比 希尔排序算法原理细节分析代码实现复杂度分析稳定性分析 总结对比 插入排序 算法原理 插入排序又或者说直接插入排序,是一种和冒泡排序类似的并且比较简单的排序方法, 基本思想…...

JDK1.8对HashMap的优化、以及通过源码解析1,8扩容机制
JDK 1.8 对 HashMap 进行了一些优化,主要包括以下几个方面的改进: 红黑树:在 JDK 1.8 中,当哈希碰撞(多个键映射到同一个桶)达到一定程度时,HashMap 会将链表转化为红黑树,以提高查找…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
