排序-算法
文章目录
- 一、排序的概念及引用
- 1.1 排序概念
- 1.2 排序运用
- 1.3 常见排序算法
- 二、常见排序算法的实现
- 2.1 插入排序
- 2.1.1 基本思想
- 2.1.2 直接插入排序
- 2.1.3 希尔排序
- 2.2 选择排序
- 2.2.1 基本思想
- 2.2.2 直接选择排序
- 2.2.3 堆排序
- 2.3 交换排序
- 2.3.1 冒泡排序
- 2.3.2 快速排序
- 2.3.3 快速排序优化
- 2.3.4 快速排序非递归
- 2.4 归并排序
- 2.4.1 基本思想
- 2.4.2 海量数据的排序问题
- 三、排序算法复杂度及稳定性分析
- 四、其他非基于比较排序
- 1.计数排序
- 2.基数排序
- 3.桶排序
- 五.选择题
一、排序的概念及引用
1.1 排序概念
排序:使一串数据,按照其中某个或某些关键字的大小,递增或递减排列起来的操作。(本文所讲排序都是按升序排列。)
稳定性:假设在待排序的记录序列中,存在多个具有相同的关键字,若经过排序,这些数据的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。

内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 排序运用

1.3 常见排序算法

二、常见排序算法的实现
2.1 插入排序
2.1.1 基本思想
把待排序的数据集合按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有数据插入完为止,得到一个新的有序序列。

2.1.2 直接插入排序
初始时,第一个元素为有序序列,从第二个元素i所指的值(tmp)开始,与前面的有序序列的末尾下标j所指值开始进行比较,如果j所指的值大于tmp,j所指元素向后移,直到j所指的值小于等于tmp,j后一位存放tmp,i向后走重复上述步骤。

public static void insertSort(int[] array){for(int i = 1;i < array.length; i++){int j = i-1;int tmp = array[i];for(;j >= 0;j--){if(array[j] > tmp){array[j+1] = array[j];}else {break;}}array[j+1] = tmp;}}
直接插入排序的特性总结:
1. 元素集合越有序,算法的时间效率越高 ,适用于待排序序列 已经基本上趋于有序了
2. 时间复杂度:最坏情况O(N^2) 最好情况O(N)
3. 空间复杂度:O(1)
4. 稳定性:稳定
2.1.3 希尔排序
希尔排序法又称缩小增量法,基本思想:先选定一个整数gab,把待排序集合中所有元素分成多个组,所有距离为gab的元素分在同一组,并对每一组内的记录进行插入排序。然后设定一个新的整数,重复上述分组和排序的工作。当到达=1时,所有记录在一组内排好序。

/**
* 希尔排序
*/
public static void shellSort(int[] array){int gab = array.length;while (gab >1){gab /= 2;shell(array,gab);}}
/**
* 将array分为gab组进行插入排序
*/
private static void shell(int[] array,int gab){for (int i = gab; i < array.length; i++) {int j = i-gab;int tmp = array[i];for (;j >= 0; j -= gab){if (array[j] > tmp){array[j+gab] = array[j];}else {break;}}array[j+gab] = tmp;}
}
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让集合更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定,按O(N1.25)到O(1.6*N1.25)来算
- 稳定性:不稳定
2.2 选择排序
2.2.1 基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列起始位置,直到全部待排序的数据元素排完。
2.2.2 直接选择排序
以i=0遍历数组,从i开始的数中找到最小(大)值下标minindex(maxindex),minindex(maxindex)和i位置的值进行交换。

public static void selectSort(int[] array){for (int i = 0; i < array.length; i++) {//记录最小值下标int minindex = i;for (int j = i+1; j <array.length ; j++) {if (array[j] < array[minindex]){minindex = j;}}//最小值不是i位置的数据if(minindex != i){swap(array,minindex,i);}}
}
//交换
private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}
双向选择排序:
1.从数组指定区间(left,right)内找到最小值和最值下标—minindex与maxindex
2.将其与区间端点值进行交换,缩小区间重复执行上述操作,直到区间只剩下一个元素

public static void selectSort(int[] array){int left = 0;int right = array.length-1;while(left < right){int minindex = left;int maxindex = left;for (int i = left; i <= right; i++) {if (array[i] < array[minindex]){minindex = i;}if(array[i] > array[maxindex]){maxindex = i;}}//走到这里,minindex和maxindex是区间(left,right)内的最小值和最值下标//最小值不是区间第一个元素if (minindex != left){swap(array,minindex,left);}swap(array,maxindex,right);left++;right--;}
}
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好,实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
2.2.3 堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。
步骤:
1.建堆----升序建大根堆,降序建小根堆
2.利用堆删除思想进行排序
public static void heapSort(int[] array){//创建大根堆createHeap(array);//利用堆删除思想进行排序int end = array.length-1;while(end > 0){swap(array,0,end);sifiDown(array,0,end);end--;}
}
/**
* 创建大根堆
*/
private static void createHeap(int[] array){//从最后一颗子树开始向下调整for (int parent = (array.length-1)/2; parent >=0 ; parent--) {sifiDown(array,parent,array.length);}
}
/**
* 向下调整
*/
private static void sifiDown(int[] array,int parent,int length){int child = 2*parent+1;//至少存在左孩子while(child < length){//存在右孩子 且 右孩子值大于左孩子if(child+1 < length && array[child] < array[child+1]){child++;}//走到这里,child是孩子节点最大值的下标//父亲节点的值小于最大孩子节点值if(array[parent] < array[child]){swap(array,parent,child);//子树向下调整parent = child;child = parent*2+1;}else {break;}}
}
堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N* log 2 N \log_{2}N log2N)
- 空间复杂度:O(1)
- 稳定性:不稳定
2.3 交换排序
基本思想:比较序列中两个值,如果不满足排序要求,交换两个值,交换排序的特点是:将值较大的向序列的尾部移动,值较小的向序列的前部移动。
2.3.1 冒泡排序
j遍历集合,j和j+1对应的值比较,如果j对应值大于j+1对应值,交换,j向后走直至j指向最后一个元素,一趟排序结束,需要比较n-1趟,冒泡排序特点:每一趟确定一个数的位置且位置在待排序序列最后,下一趟就可以少比较一个数,趟数为n-1(n是集合中元素的个数),如果本趟没有进行交换,说明集合已经排好序。
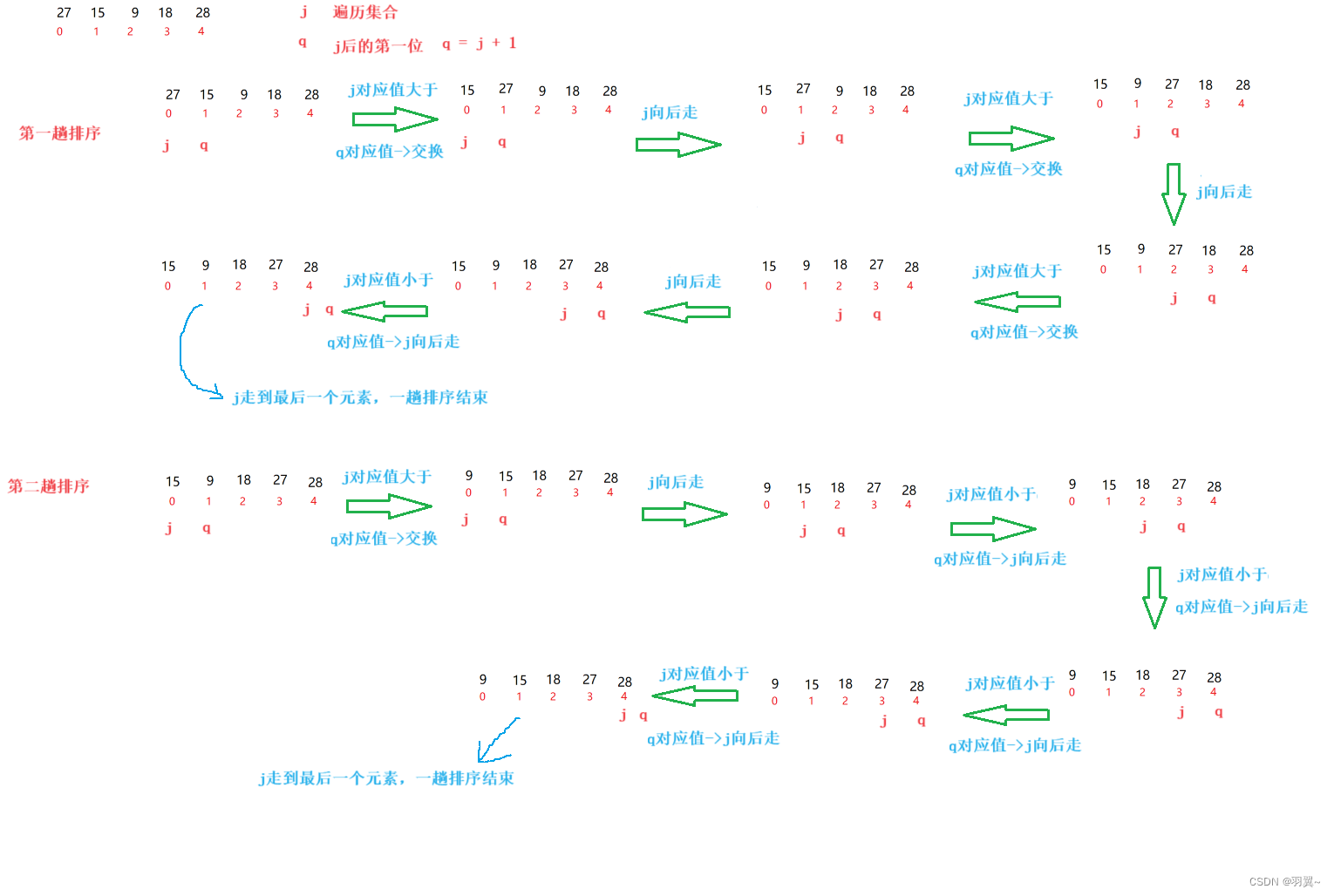
public static void bubbleSort(int[] array){//i表示趟数for (int i = 0; i < array.length-1; i++) {boolean flog = false;for (int j = 0; j < array.length-1-i; j++) {if(array[j] > array[j+1]){swap(array,j,j+1);flog = true;}}if(!flog){break;}}
}//交换private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
2.3.2 快速排序
以区间内第一个数为基准值,将整个区间划分为两个子序列,左子序列都是比基准值小的数,右子序列都是比基准值大的数;对左、右子序列为新的区间进行前面操作,直至区间只存在一个元素。
public static void quick(int[] array,int left,int right){//区间不存在或区间只有一个元素if(left >= right){return;}//按基准值对数组的(left,right)区间进行划分 并返回基准值所在下标int pivot = partion(array,left,right);//对数组的(left,pivot)区间进行快速排序quick(array,left,pivot-1);//对数组的(pivot+1,right)区间进行快速排序quick(array,pivot+1,right);}
将区间按照基准值划分为左右两半部分的常见方式有:
1. Hoare 版

private static int partion(int[] array,int left,int right){int tmp = array[left];int i = left;while(left < right){while (left < right && array[right] >=tmp){right--;}while(left < right && array[left] <= tmp){left++;}swap(array,left,right);}swap(array,i,left);return left;}
2. 挖坑法

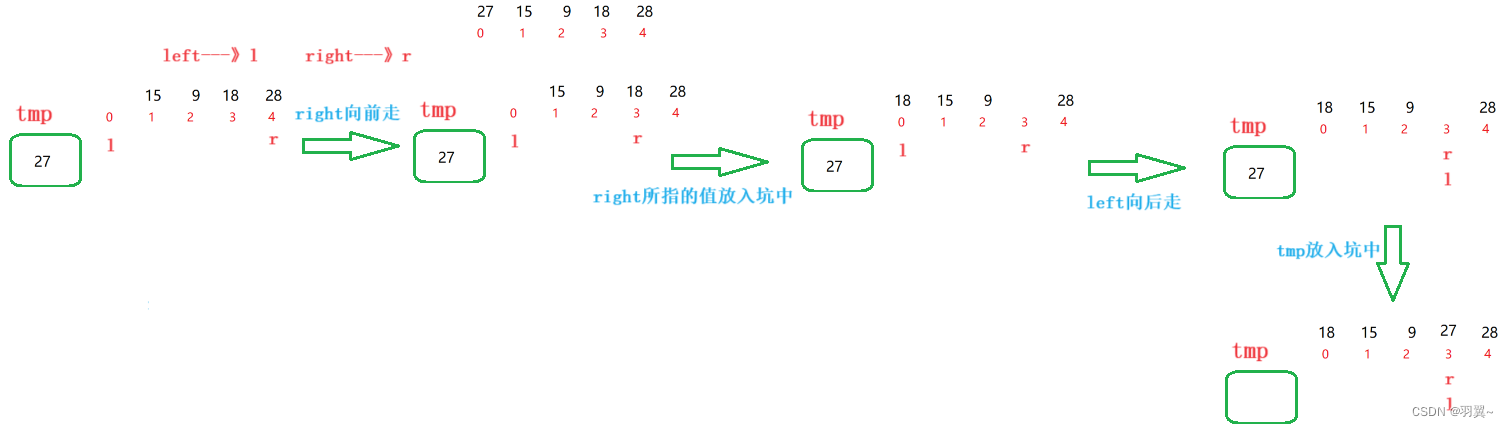
private static int partion(int[] array,int left,int right){int tmp = array[left];while (left < right){while (left < right && array[right] > tmp){right--;}//走到这,right是比基准值小的下标或left == rightarray[left] = array[right];while (left < right && array[left] <tmp){left++;}//走到这,left是比基准值大的下标或left == rightarray[right] = array[left];}//基准值放入坑中array[left] = tmp;return left;}
3. 前后指针法

写法一
private static int partion(int[] array,int left,int right){int prev = left;int cur = left+1;while (cur <= right){if(array[cur] < array[left] && array[++prev] != array[cur]){swap(array,cur,prev);}cur++;}swap(array,left,prev);return prev;
}
写法二
private static int partition(int[] array, int left, int right) {int d = left + 1;int pivot = array[left];for (int i = left + 1; i <= right; i++) {if (array[i] < pivot) {swap(array, i, d);d++;}}swap(array, d - 1, left);return d - 1;
}
2.3.3 快速排序优化
1.三数取中法选key
在下标为left(区间第一个数下标)、right(区间最后一个数下标)和mid(区间中间数下标)对应数值中找到中间数,与区间第一个数进行交换,使得以基准值(区间第一个数)划分的尽可能使左右区间都超过一个数,从而减少递归次数。
private static void quick(int[] array,int start,int end) {if(start >= end) {return;}//1 2 3 4 5 6 7int index = middleNum(array,start,end);swap(array,index,start);//4 2 3 1 5 6 7int pivot = partition(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);
}
/**
* 求中位数的下标
*/
private static int middleNum(int[] array,int left,int right) {int mid = (left+right)/2;if(array[left] < array[right]) {if(array[mid] < array[left]) {return left;}else if(array[mid] > array[right]) {return right;}else {return mid;}}else {//array[left] > array[right]if(array[mid] < array[right]) {return right;}else if(array[mid] > array[left]) {return left;}else {return mid;}}
}
2. 递归到小的子区间时,可以考虑使用插入排序
private static void quick(int[] array,int start,int end) {if(start >= end) {return;}//区间比较小if(end - start + 1 <= 15) {insertSort(array, start, end);return;}int pivot = partition(array,start,end);quick(array,start,pivot-1);quick(array,pivot+1,end);
}
public static void insertSort(int[] array,int left,int right) {for (int i = left+1; i <= right; i++) {int tmp = array[i];int j = i-1;for (; j >= left ; j--) {if(array[j] > tmp) {array[j+1] = array[j];}else {break;}}array[j+1] = tmp;}
}
2.3.4 快速排序非递归
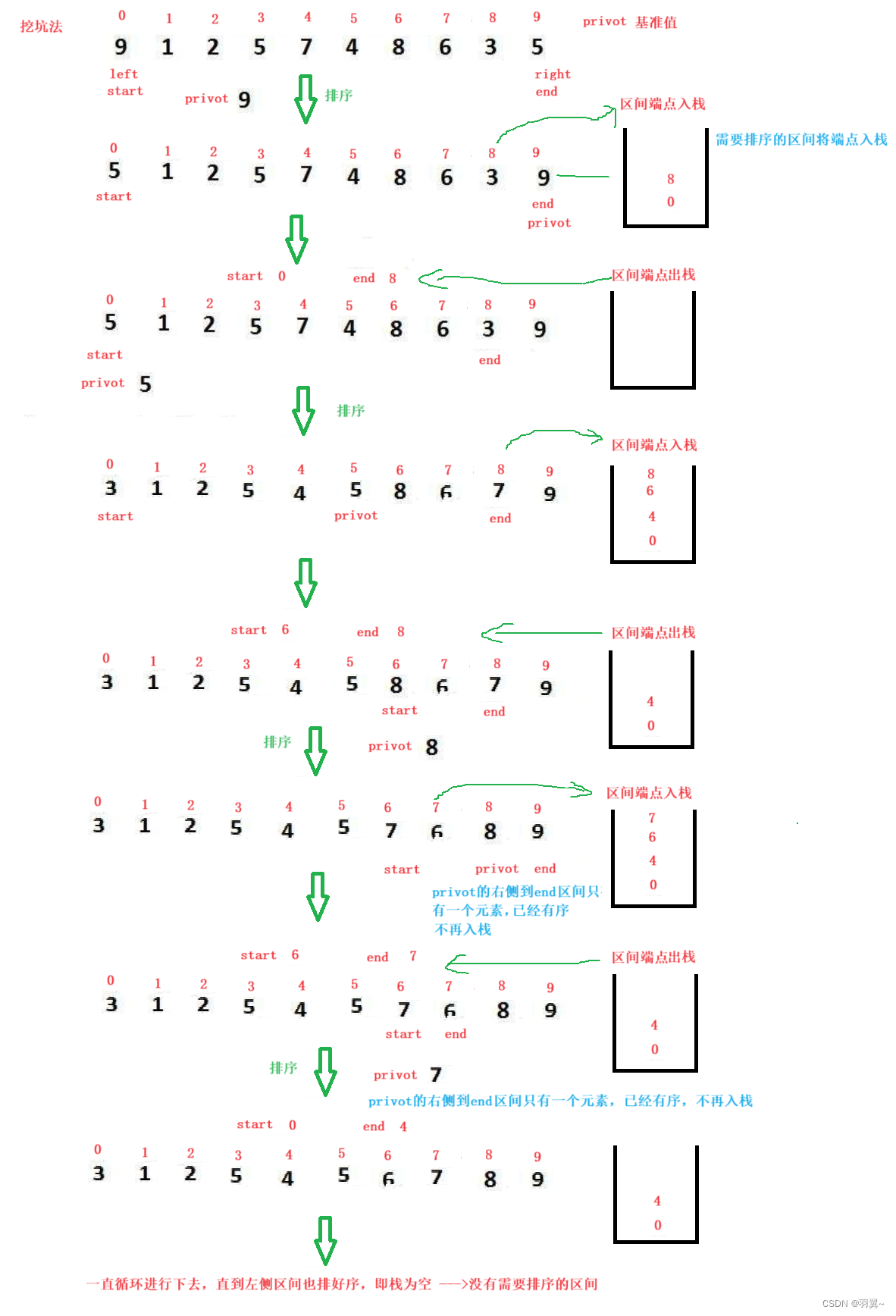
/**快速排序非递归
*/
public static void quickSortNor(int[] array){int start = 0;int end = array.length-1;//存放要排序的区间端点下标Stack<Integer> stack = new Stack<>();//基准值下标int privot = partion(array,start,end);//基准值的左边(左区间)的元素至少有2个if(privot-1 > start){stack.push(start);stack.push(privot-1);}//基准值的右边(右区间)的元素至少有2个if(privot+1 < end){stack.push(privot+1);stack.push(end);}while ( !stack.isEmpty()){end = stack.pop();start = stack.pop();privot = partion(array,start,end);//基准值的左边(左区间)的元素至少有2个if(privot-1 > start){stack.push(start);stack.push(privot-1);}//基准值的右边(右区间)的元素至少有2个if(privot+1 < end){stack.push(privot+1);stack.push(end);}}
}
快速排序总结:
1.快速排序整体的综合性能和使用场景都比较好
2.时间复杂度:O(N*logN)
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
2.4 归并排序
2.4.1 基本思想
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
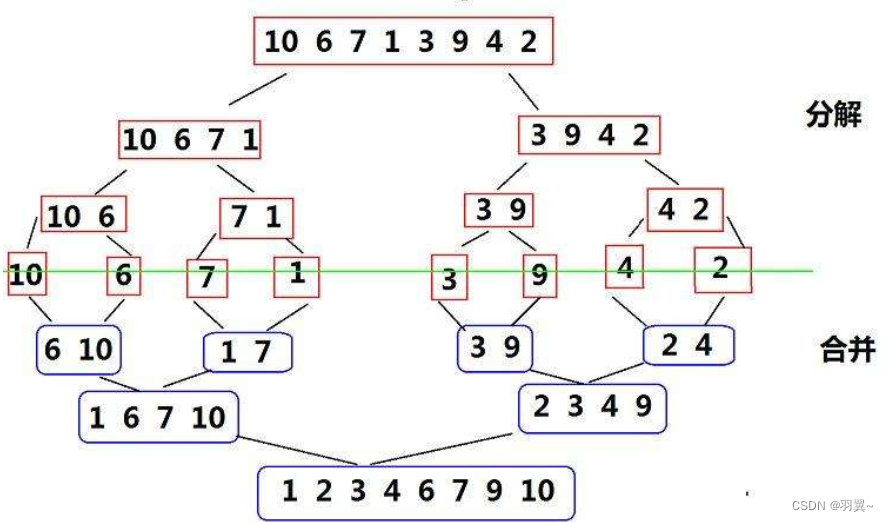
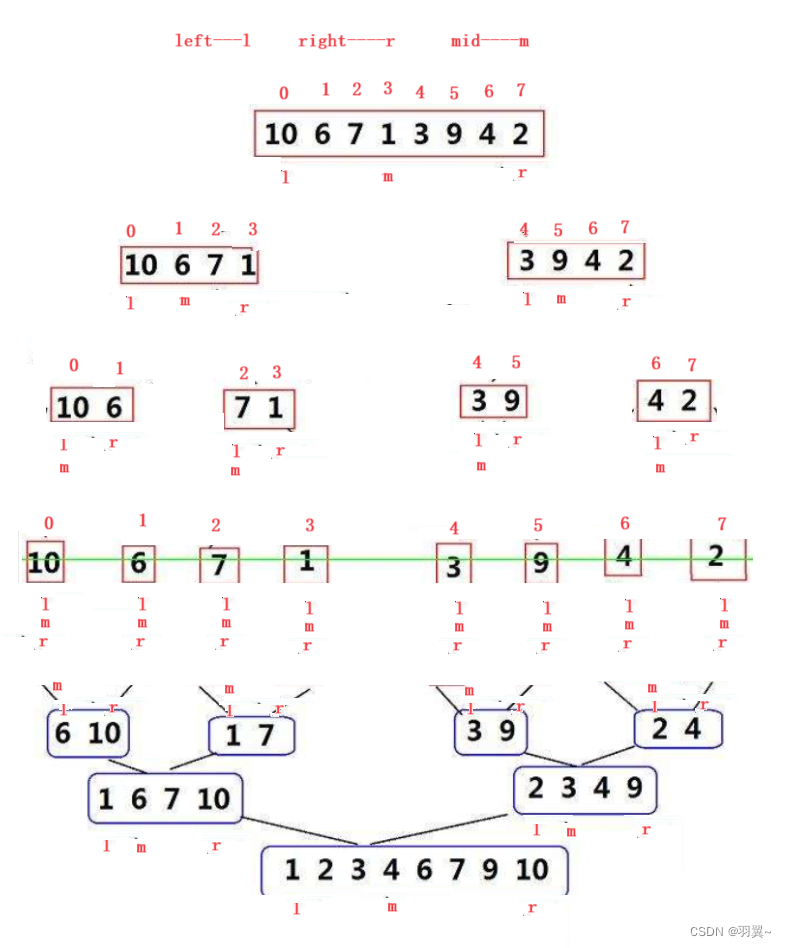
/**递归实现排序*/public static void mergeSort(int[] array){merge(array,0,array.length-1);
}
private static void merge(int[] array, int left, int right) {if(left >= right){return;}int mid = (left + right)/ 2;//划分为两组merge(array,left,mid);merge(array,mid+1,right);//合并combine(array,left,mid,right);
}
/**合并两个有序数组
*/
private static void combine(int[] array, int left, int mid, int right) {//第一个数组的区间端点下标int s1 = left;int e1 = mid;//第二个数组的区间端点下标int s2 = mid+1;int e2 = right;//新数组的长度int length = right-left+1;int[] arr = new int[length];//新数组下标int k = 0;//合并while( s1 <= e1 && s2 <= e2){if(array[s1] < array[s2]){arr[k++] = array[s1++];}else {arr[k++] = array[s2++];}}while (s1 <= e1){arr[k++] = array[s1++];}while (s2 <= e2){arr[k++] = array[s2++];}//将合并的新数组放入原来数组对应位置for (int i = 0; i < arr.length; i++) {array[i+left] = arr[i];}
}`
//非递归
public static void mergeSortNor(int[] array){//每个子序列元素个数int gap = 1;while( gap < array.length){for (int i = 0; i < array.length; i+=gap*2) {//left 代表一组的第一个元素下标int left = i;//mid 代表此组最后一个元素下标int mid = left+gap-1;if(mid >= array.length){mid = array.length-1;}//right 代表下一组的最后一个元素下标int right = mid+gap;if(right >= array.length){right = array.length-1;}combine(array,left,mid,right);}gap *= 2;}
}
归并排序总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序更多是解决在磁盘中的外排序问题
- 时间复杂度: O(N*logN)
- 空间复杂度:O(logN)
- 稳定性:稳定
2.4.2 海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
- 先把文件切分成 200 份,每个 512 M
- 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
- 进行 2路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
三、排序算法复杂度及稳定性分析
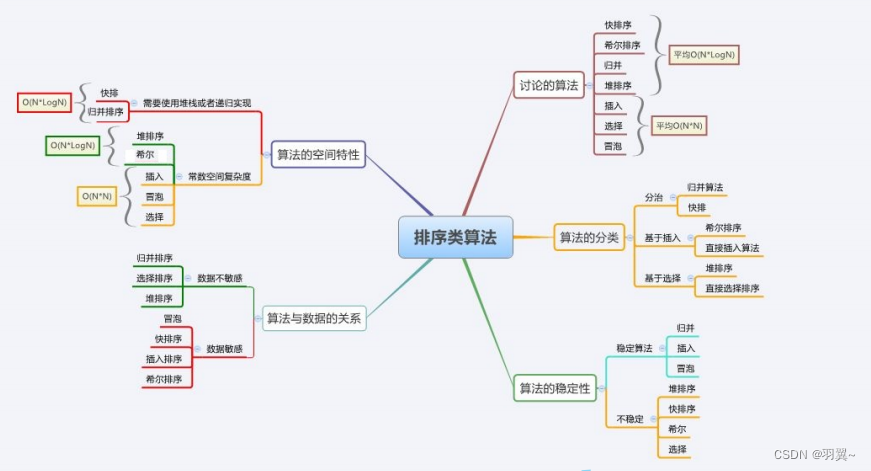
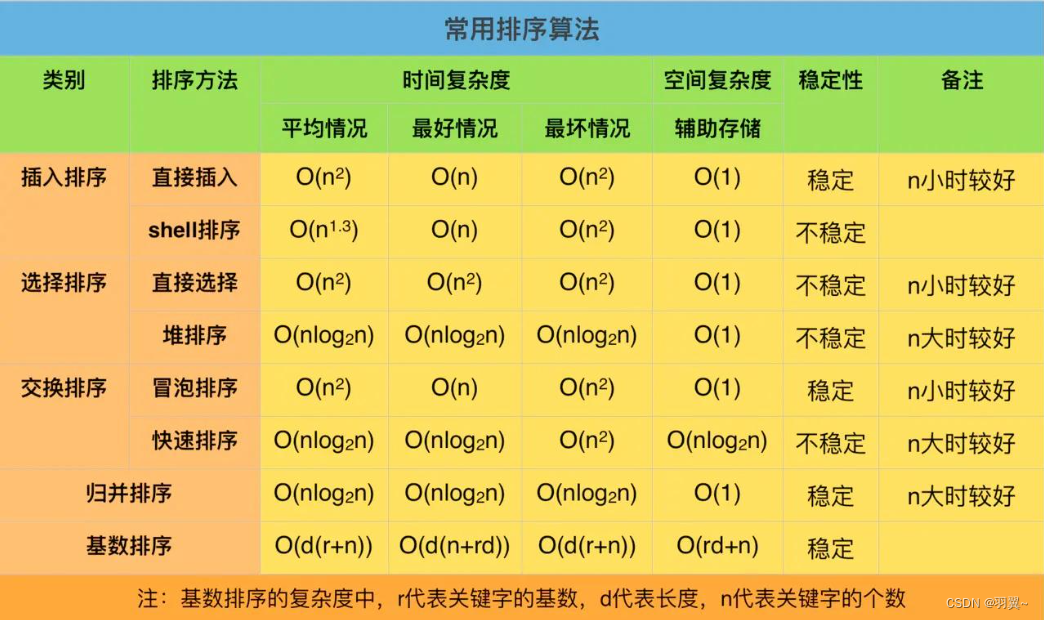
四、其他非基于比较排序
1.计数排序
计数排序以数组来实现,数组的下标是待排序序列值,数组存储的是元素出现的个数。操作步骤:
- 统计待排序序列中各个元素的个数到新数组
- 遍历新数组,将原序列进行覆盖
public static void countSort(int[] array){//获取集合中的最大值和最小值int minvalue = array[0];int maxvalue = array[0];for (int i = 0; i < array.length; i++) {if(array[i] < minvalue){minvalue = array[i];}if(array[i] > maxvalue){maxvalue = array[i];}}//新建数组长度int length = maxvalue-minvalue+1;//以数组值存储元素的个数,数组的下标值为元素值-minvalue的结果int[] count = new int[length];//记录集合中元素个数for (int i = 0; i < array.length; i++) {count[array[i]-minvalue]++;}//array下标int k = 0;//遍历count数组,将实际值重写回array中for (int i = 0; i < count.length; i++) {while( count[i] > 0){array[k++] = i+minvalue;count[i]--;}}
}
计数排序总结:
3. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
4. 时间复杂度:O(MAX(N,范围))
5. 空间复杂度:O(范围)
6. 稳定性:稳定
2.基数排序
基数排序
3.桶排序
桶排序
五.选择题
1. 快速排序算法是基于()的一个排序算法。
A:分治法 B:贪心法 C:递归法 D:动态规划法
2.对记录(54,38,96,23,15,72,60,45,83)进行从小到大的直接插入排序时,当把第8个记录45插入到有序表时,为找到插入位置需比较()次?(采用从后往前比较)
A: 3 B: 4 C: 5 D: 6
3.以下排序方式中占用O(n)辅助存储空间的是()
A: 简单排序 B: 快速排序 C: 堆排序 D: 归并排序
4.下列排序算法中稳定且时间复杂度为O(n^2)的是()
A: 快速排序 B: 冒泡排序 C: 直接选择排序 D: 归并排序
5.关于排序,下面说法不正确的是()
A: 快排时间复杂度为O(N*logN),空间复杂度为O(logN)
B: 归并排序是一种稳定的排序,堆排序和快排均不稳定
C: 序列基本有序时,快排退化成 "冒泡排序",直接插入排序最快
D: 归并排序空间复杂度为O(N), 堆排序空间复杂度的为O(logN)
6.设一组初始记录关键字序列为(65,56,72,99,86,25,34,66),则以第一个关键字65为基准而得到的一趟快速排序结果是()
A: 34,56,25,65,86,99,72,66 B: 25,34,56,65,99,86,72,66
C: 34,56,25,65,66,99,86,72 D: 34,56,25,65,99,86,72,66答案:1.A 2.C 3.D 4.B 5.D 6.A
相关文章:

排序-算法
文章目录 一、排序的概念及引用1.1 排序概念1.2 排序运用1.3 常见排序算法 二、常见排序算法的实现2.1 插入排序2.1.1 基本思想2.1.2 直接插入排序2.1.3 希尔排序 2.2 选择排序2.2.1 基本思想2.2.2 直接选择排序2.2.3 堆排序 2.3 交换排序2.3.1 冒泡排序2.3.2 快速排序2.3.3 快…...
【特纳斯电子】基于单片机的火灾监测报警系统-实物设计
视频及资料链接:基于单片机的火灾监测报警系统-实物设计 - 电子校园网 (mcude.com) 编号: T0152203M-SW 设计简介: 本设计是基于单片机的火灾监测报警系统,主要实现以下功能: 1.通过OLED显示温度、烟雾、是否有火…...
网络安全就业形势怎么样?
泻药,以下都是我本人的肺腑之言,是答主深耕职场多年,转战数家公司总结周围朋友的从业经验才总结出来的行业真相,真心希望帮助到还没有步入职场的大家,尤其是24届的应届毕业生,多掌握些就业信息就能少走一些…...
【Golang】Go的并发和并行性解释。谁说Go不是并行语言?
偶然发现百度上有很多"师出同门"的"go是并发语言,而不是并行语言"的说法。让我顿感奇怪,"并行"说白了就是对CPU多核的利用,这年头不能利用多核的编译语言还有的混?而且还混的这么好?并且…...
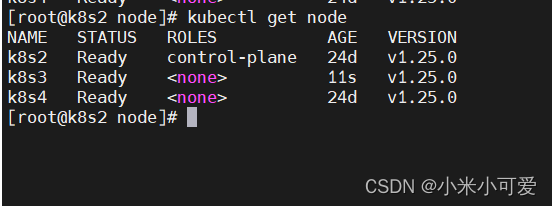
k8s-16 k8s调度
调度器通过 kubernetes 的 watch 机制来发现集群中新创建且尚未被调度到 Node上的 Pod。调度器会将发现的每一个未调度的 Pod 调度到一个合适的 Node 上来运行。 kube-scheduler 是 Kubernetes 集群的默认调度器,并且是集群控制面的一部分如果你真的希望或者有这方面…...
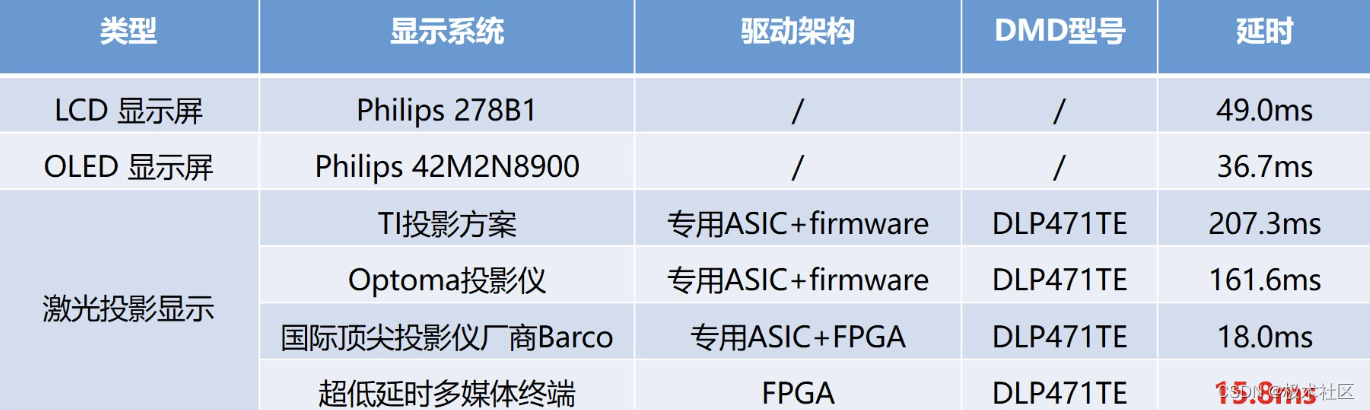
【2023研电赛】全国技术竞赛一等奖:基于FPGA的超低时延激光多媒体终端
该作品参与极术社区组织的研电赛作品征集活动,欢迎同学们投稿,获取作品传播推广,并有丰富礼品哦~ 基于FPGA的超低时延激光多媒体终端 参赛单位:华东师范大学 指导老师:刁盛锡 参赛队员:王泽宇 谢祖炜 秦子淇…...
Annoy vs Milvus:哪个向量数据库更适合您的AI应用?知其然知其所以然
1. Annoy vs Milvus简介 Annoy 和 Milvus 都是用于向量索引和相似度搜索的开源库,它们可以高效地处理大规模的向量数据。 Annoy(Approximate Nearest Neighbors Oh Yeah): Annoy 是一种近似最近邻搜索算法,它通过构…...
)
android 13.0 SystemUI导航栏添加虚拟按键功能(一)
1.概述 在13.0的系统产品开发中,在系统SystemUI的原生系统中默认只有三键导航,想添加其他虚拟按键就需要先在构建导航栏的相关布局中分析结构,然后添加相关的图标xml就可以了,然后添加对应的点击事件,就可以了,接下来先分析第一步关于导航栏的相关布局情况 然后实现功能 …...

内存管理-分页、虚拟地址、虚拟内容、页面置换算法
文章目录 一、5W2H角度分析内存管理What是内存管理Why需要内存管理Who使用内存管理Where内存管理应用When需要内存管理How内存管理工作How much内存管理的成本 二、分页什么是分页分页的原理分页的优缺点分页的应用 三、虚拟地址什么是虚拟地址虚拟地址的作用虚拟地址的转换虚拟…...
【C++入门】命名空间详解(从零开始,冲击蓝桥杯)
C入门 命名空间 南喵小鸡汤程序员可以让步,却不可以退缩,可以羞涩,却不可以软弱,总之,程序员必须是勇敢的。一 . 命名空间的介绍二.命名空间的实际应用1.为什么要有命名空间我们在使用变量时,通常会为他定义一个名字,在…...
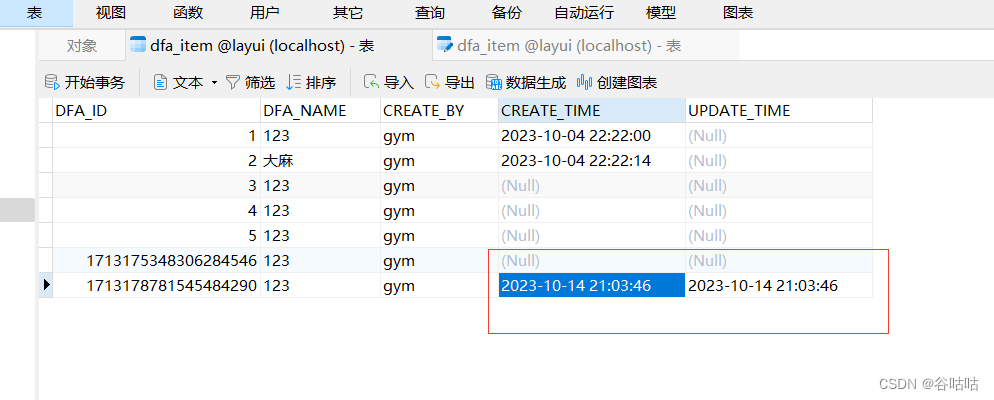
通过代码MyBatis-plus实现对表中createTime和updateTime进行自动更新
通过代码MyBatis-plus实现对表中createTime和updateTime进行自动更新 实现这样的效果可以在数据库中设置,但是我们一般建议在代码里实现, 但是总不能每次insert和update的时候都手写new当前时间 因此推荐使用mybatis-plus 1导入依赖 <dependency&g…...
)
HTML 实时显示本地电脑时间(精确到毫秒)
<!DOCTYPE html> <html> <head><title>实时显示本地电脑时间(精确到毫秒)</title> </head> <body><h1>本地电脑时间(精确到毫秒):</h1><h1 id"clock&q…...

opencv跨平台arm交叉编译之ubuntu
目录 1. 安装交叉编译工具链2. 安装依赖3. 配置工具链3.1 新建build目录3.2 安装cmake-gui3.3 工具链配置界面进行配置3.3.1 终端输入以下命令3.3.2 点击Configure,弹出编译方式选择对话框:3.3.3 点击Next3.3.4 点击Finish3.3.5 点击Configure。3.3.6 Ge…...

Git命令全集
1、克隆代码 查看项目地址 git remote -v直接克隆 git clone url克隆指定分支 git clone -b 分支 git地址RPC failed错误:修改Git的传输字节限制 git config --global http.postBuffer 10485760002、查看分支 查看 git branch -a切换分支 git branch 分支名从指定分支…...
[BigData:Hadoop]:安装部署篇
文章目录 一:机器103设置密钥对免密登录二:机器102设置密钥对免密登录三:机器103安装Hadoop安装包3.1:wget拉取安装Hadoop包3.2:解压移到指定目录3.2.1:解压移动路径异常信息3.2.2:切换指定目录…...

ubuntu 上vscode使用cmake编译运行c++程序
参考:ubuntu 上vscode使用cmake编译运行c程序_vscode ubuntu运行c程序_SCH0的博客-CSDN博客 文章是对官方过程的翻译: Get started with CMake Tools on Linux...

Node.js 新特性 SEA/单文件可执行应用尝鲜
#1 关于 SEA 单文件可执行应用(SEA,Singe Executable Applications),是 Node.js 新版本的特性,最初在 v19.7.0、v18.16.0 加入,并在 v20.x 得到扩展。而上个月发布的全家桶 Bun.js,就自带了 SEA…...

137.只出现一次的数字II
137. 只出现一次的数字 II - 力扣(LeetCode) 给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法且使用常数级空间来…...
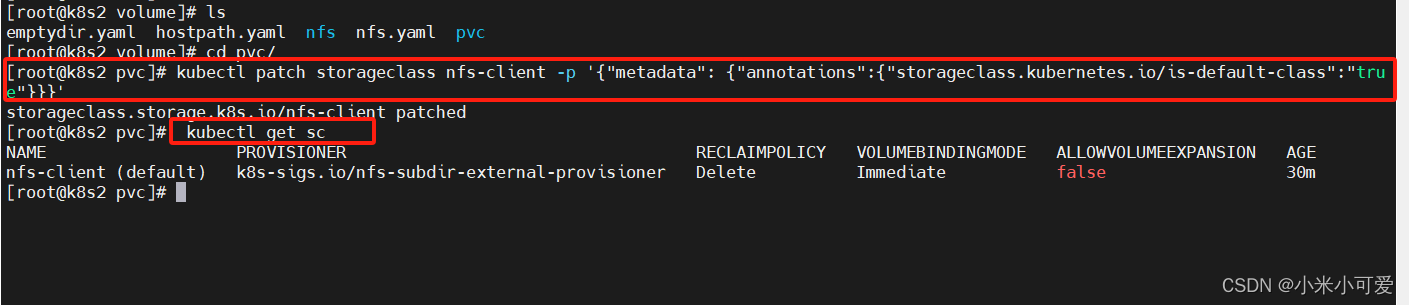
k8s-15 strogeclass
官网: https://github.com/kubernetes-sigs/nfs-subdir-external-provisioner StorageClass提供了一种描述存储类 (class)的方法,不同的cass可能会映射到不同的服务质量等级和备份策略或其他策略等 每个 StorageClass 都包含 provisioner、parameters 和…...

微信小程序开发实战:利用差异对比显示对象属性变化
前言 在小程序开发中,经常会遇到需要比较两个对象之间的差异并将这些差异可视化展示在界面上的情况。这一过程对于数据管理和用户反馈至关重要。本文将介绍一种实用的方法,可以帮助开发者高效地比较两个对象的属性差异,并将这些差异以直观的方…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
