【CFD小工坊】浅水模型的边界条件
【CFD小工坊】浅水模型的边界条件
- 前言
- 处理边界条件的原则
- 边界处水力要素的计算
- 水位边界条件
- 单宽流量边界条件
- 流量边界条件
- 固壁边界条件
- 参考文献
前言
在浅水方程的离散及求解方法一篇中,我们学习了三角形网格各边通量值及源项的求解。但仍有一个问题没有解决:对于边界处的网格,模型边界对应的网格边的通量求解。
对此,我们借鉴王志力1的研究,学习各类边界条件下,网格边的通量的求解。
处理边界条件的原则
对于浅水水域,常见的边界有水位边界与流量边界。在此,我们假设网格 i i i的第 j j j条边对应了模型的边界,设边界上的水位为 h i j ∗ h_{ij}^* hij∗,垂直(外法线方向)和平行网格边的流速为 u ~ i j ∗ \tilde{u}_{ij}^* u~ij∗和 v ~ i j ∗ \tilde{v}_{ij}^* v~ij∗。为简便起见,以下我们将 h i j ∗ h_{ij}^* hij∗简记为 h ∗ h^* h∗,将 u ~ i j ∗ \tilde{u}_{ij}^* u~ij∗和 v ~ i j ∗ \tilde{v}_{ij}^* v~ij∗简记为 u ~ L ∗ \tilde{u}_L^* u~L∗和 v ~ L ∗ \tilde{v}_L^* v~L∗
根据一维方程的特征线理论,沿着特征线方向有特征不变量,最终会得到如下关系:
u ~ L ∗ + 2 c L = u ∗ + 2 c ∗ \tilde{u}_L^*+2c_L = u^* + 2c^* u~L∗+2cL=u∗+2c∗
上式即确定边界条件时所要满足的原则。其中, c L = g h L c_L=\sqrt{gh_L} cL=ghL, c ∗ = g h ∗ c^*=\sqrt{gh^*} c∗=gh∗。
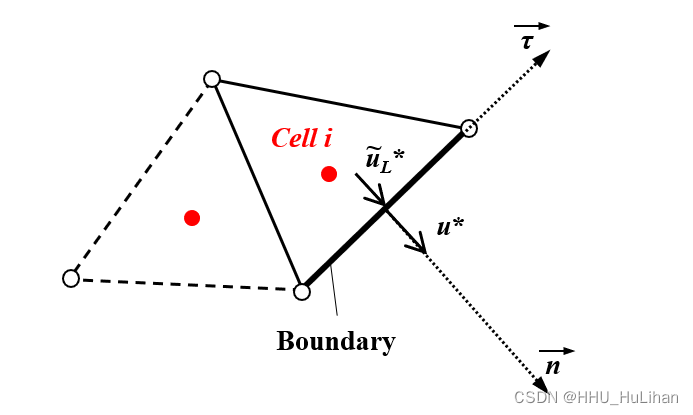
边界处水力要素的计算
在模型中,边界处的水力要素的计算步骤如下:
- 根据笛卡尔坐标系下边界处的 u L u_L uL和 v L v_L vL转化为网格边界外法线方向和切向的 u ~ L ∗ \tilde{u}_L^* u~L∗和 v ~ L ∗ \tilde{v}_L^* v~L∗。
- 给定边界处的 u ∗ u^* u∗或 h ∗ h^* h∗。此处的 u ∗ u^* u∗值可通过流量边界条件转化而来。
- 根据式 u ~ L ∗ + 2 c L = u ∗ + 2 c ∗ \tilde{u}_L^*+2c_L = u^* + 2c^* u~L∗+2cL=u∗+2c∗来确定网格边上的其它变量。例如,对于水位条件, h ∗ h^* h∗已知,我们需要通过上式确定 u ∗ u^* u∗。
- 根据浅水方程的对流项确定通量值。
水位边界条件
对于边界条件, h ∗ h^* h∗已知,则:
u ∗ = u ~ L ∗ + 2 c L − 2 c ∗ = u ~ L ∗ + 2 g h L − 2 g h ∗ u^* = \tilde{u}_L^*+2c_L - 2c^*=\tilde{u}_L^*+ 2\sqrt{gh_L} -2\sqrt{gh^*} u∗=u~L∗+2cL−2c∗=u~L∗+2ghL−2gh∗
之后将局部坐标系的 u ∗ u^* u∗和 v ∗ v^* v∗转化为全局笛卡尔坐标系下的 u b u_b ub和 v b v_b vb;记 h b = h ∗ h_b=h^* hb=h∗。则边界处的通量为:
( F n ) b = E ( U b ) n x + G ( U b ) n y = n x ( h u b h u b 2 + g h b 2 2 h u b v b ) + n y ( h v b z h u b v b h v b 2 + g h b 2 2 ) (\bold{F}_n)_b = \bold{E(U_b)} n_x+ \bold{G(U_b)} n_y = n_x \left( \begin{matrix} hu_b \\ hu_b^2+\dfrac{gh_b^2}{2} \\ hu_b v_b \end{matrix} \right) + n_y \left( \begin{matrix} hv_bz \\ hu_b v_b \\ hv_b^2+\dfrac{gh_b^2}{2} \end{matrix} \right) (Fn)b=E(Ub)nx+G(Ub)ny=nx hubhub2+2ghb2hubvb +ny hvbzhubvbhvb2+2ghb2
式中, ( n x , n y ) (n_x, n_y) (nx,ny)表示边界处外法线方向。
单宽流量边界条件
给定网格边的单宽流量 q = h ∗ u ∗ q=h^*u^* q=h∗u∗,则有:
u ~ L ∗ + 2 c L = u ∗ + 2 c ∗ = q h ∗ + 2 g h ∗ = q c ∗ 2 / g + 2 g h ∗ \tilde{u}_L^*+2c_L = u^* + 2c^* = \dfrac{q}{h^*} + 2\sqrt{gh^*} = \dfrac{q}{{c^*}^2/g} + 2\sqrt{gh^*} u~L∗+2cL=u∗+2c∗=h∗q+2gh∗=c∗2/gq+2gh∗
化简后,上述方程为 c ∗ c^* c∗的一元三次方程:
2 c ∗ 3 − ( u L + 2 g h L ) c ∗ 2 − g q = 0 2{c^*}^3 - (u_L + 2\sqrt{gh_L}){c^*}^2 - gq = 0 2c∗3−(uL+2ghL)c∗2−gq=0
求解后可得 h ∗ = c ∗ 2 / g h^*={c^*}^2/g h∗=c∗2/g。同理,我们可求得 h b h_b hb、 u b u_b ub和 v b v_b vb,以及通量 ( F n ) b (\bold{F}_n)_b (Fn)b。
注意:在设置边界时,我们需要设定单宽流量的方向;对于入流边界,单宽流量方向与边界外法线方向相反,则 q < 0 q<0 q<0;反之,对于出流边界, q > 0 q>0 q>0。
流量边界条件
若流量给定在一个网格的边上,我们可以先求该边界的单宽流量 q q q,之后按照上一小节等同的办法处理边界。若指定的边界条件涉及到m条连续的网格边(如下图边界蓝色边所示),组需要先求出每个对应网格边的单宽流量,之后再按单宽流量边界条件处理方法进行计算。
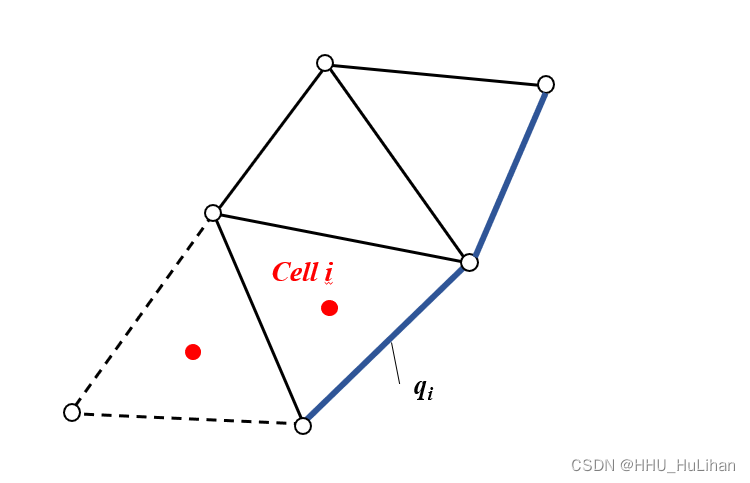
对于这m条边界上的总流量 Q Q Q,某一网格 i i i边上的单宽流量 q i q_i qi是:
q i = L i ′ h i 1.5 C i ∑ k = 1 m L k ′ h k 1.5 C k Q q_i = \dfrac{L'_i h_i^{1.5}C_i}{\sum^{m}_{k=1} L'_k h_k^{1.5}C_k} Q qi=∑k=1mLk′hk1.5CkLi′hi1.5CiQ
式中, L ′ L' L′表示流量边界对应网格边的边长, h h h表示对应网格的水深, C C C表示对应网格的摩阻力项,有 C = h 1 / 6 n C = \dfrac{h^{1/6}}{n} C=nh1/6,n为曼宁系数。
之后根据求出的单款流量,依次处理每个边界网格的通量值。
固壁边界条件
在静止的固壁边界上,我们采用无滑移边界条件,即 u b u_b ub和 v b v_b vb均为0,故:
( F n ) b = ( 0 g h L 2 2 n x g h L 2 2 n y ) (\bold{F}_n)_b = \left( \begin{matrix} 0 \\ \dfrac{gh_L^2}{2}n_x \\ \dfrac{gh_L^2}{2}n_y \end{matrix} \right) (Fn)b= 02ghL2nx2ghL2ny
参考文献
王志力. 基于Godunov和Semi-Lagrangian法的二、三维浅水方程的非结构化网格离散研究[D]. 辽宁:大连理工大学,2005. ↩︎
相关文章:

【CFD小工坊】浅水模型的边界条件
【CFD小工坊】浅水模型的边界条件 前言处理边界条件的原则边界处水力要素的计算水位边界条件单宽流量边界条件流量边界条件固壁边界条件 参考文献 前言 在浅水方程的离散及求解方法一篇中,我们学习了三角形网格各边通量值及源项的求解。但仍有一个问题没有解决&…...
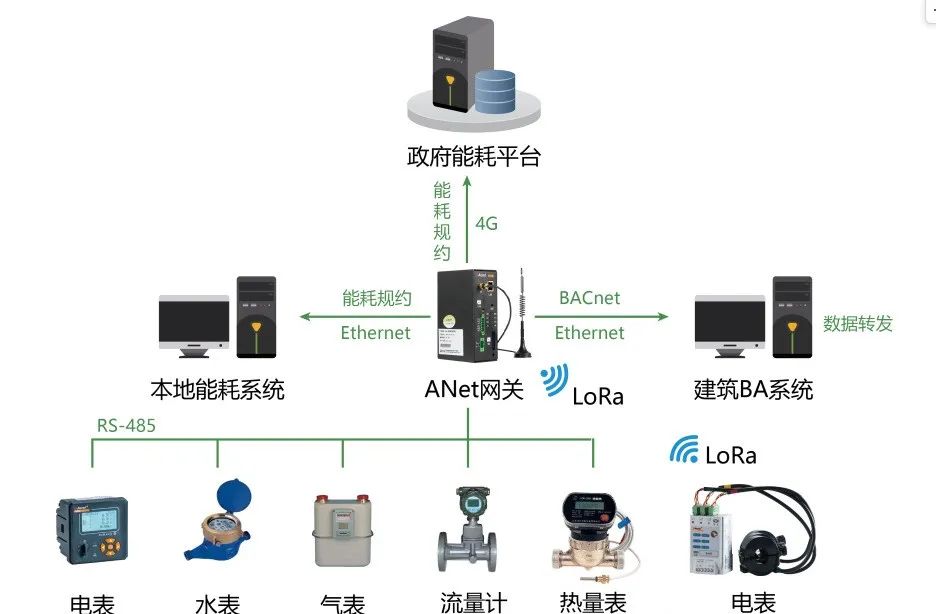
电力物联网关智能通讯管理机-安科瑞黄安南
众所周知,网关应用于各种行业的终端设备的数据采集与数据分析,然后去实现设备的监测、控制、计算,为系统与设备之间建立通讯联系,达到双向的数据通讯。 网关可以实时监测并及时发现异常数据,同时自身根据用户规则进行…...

用Flask构建一个AI翻译服务
缘起 首先,看一段代码,只有几行Python语句却完成了AI翻译的功能。 #!/usr/bin/python3import sys from transformers import MarianMTModel, MarianTokenizerdef translate(word_list):model_name "Helsinki-NLP/opus-mt-en-zh"tokenizer …...

微信小程序引入阿里巴巴iconfont图标并使用
介绍 在小程序里,使用阿里巴巴的图标,如下所示: 使用方式 搜索自己需要的图标,然后将需要用到的图标加入购物车,如下图所示: 去右上角,点击购物车按钮;这里第一次使用,会有三个提…...

mysql面试题49:MySQL中不同text数据类型的最大长度
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:MySQL中TEXT数据类型的最大长度 在MySQL中,TEXT数据类型用于存储较大…...

从虚拟电厂在上海的实践探索看企业微电网数字化的意义
安科瑞 华楠 作为典型的人口聚集、负荷密集区域,上海市具有外来电比例高、本地资源禀赋不足的特点。从发电侧角度来看,近年来上海风、光等新能源发电装机比例逐年提升,传统的火电逐渐成为调节性发电资源;从负荷侧角度来看上海以第…...

创建并初始化线程池
创建并初始化线程池–》threadpool.h, 创建并初始化&脱离(执行完后)子线程,每个子线程信号量wait阻塞【1】 创建套接字:int listenfd socket( PF_INET, SOCK_STREAM, 0 ); 端口复用:setsockopt( listenfd, SOL_SOCKET, SO_REUSEADDR, &a…...
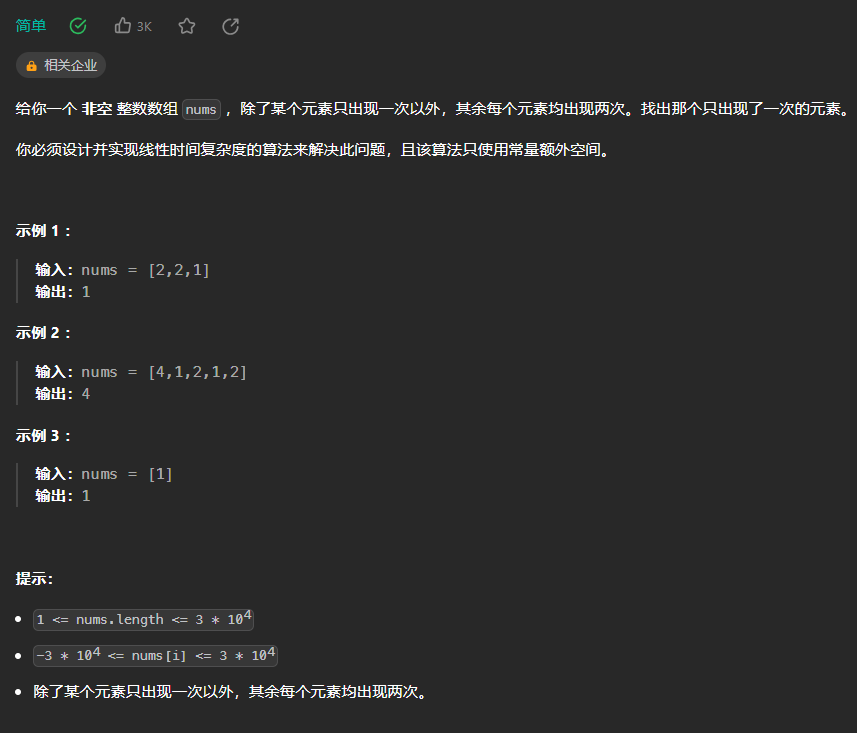
【LeetCode热题100】--136.只出现一次的数字
136.只出现一次的数字 使用哈希表: class Solution {public int singleNumber(int[] nums) {Map<Integer,Integer> map new HashMap<>();for(int num:nums){Integer count map.get(num);if(count null){count 1;}else{count;}map.put(num,count);}…...
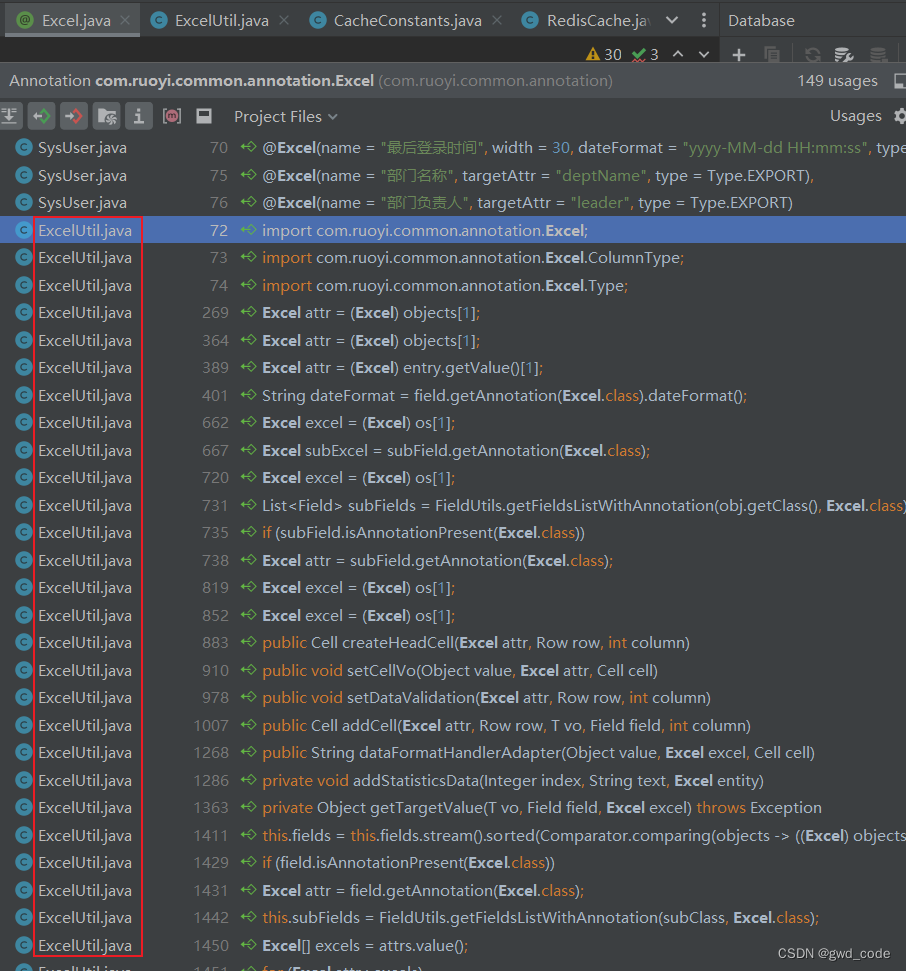
Java idea查看自定义注解的调用地方
Java idea查看自定义注解的调用地方...

ReLU激活函数
LeakyReLU激活函数的具体用法请查看此篇博客:LeakyReLU激活函数 ReLU(Rectified Linear Unit)激活函数是深度学习中最常用的激活函数之一,它的数学表达式如下: 在这里,(x) 是输入,(f(x)) 是输…...

【Android】adjustViewBounds 的理解和使用
理解 adjustViewBounds 是一个 ImageView 的属性,用于调整 ImageView 的边界以适应图像的尺寸。当设置为 true 时,ImageView 的边界将根据图像的宽高比例进行调整,以确保图像完全显示在 ImageView 内部。 理解和使用 adjustViewBounds 的步…...

Redis知识补充
大key删除 unLink scan分批删除 渐进式rehash Redis笔记:Redis的字典什么时候进行Rehash?_redis什么时候进行rehash-CSDN博客...
IIS 部署.NetCore,最细步骤
服务器安装环境 将.net core程序部署到IIS总体需要经过以下3个大步骤,其中在IIS上配置网站有些比较繁琐,我都会逐一给出详细步骤。 <1>安装IIS和.NetCORE运行时程序 <2>以文件的形式发布.NETCORE程序到指定目录 <3>IIS上面建立网站…...

4.查询用户的累计消费金额及VIP等级
思路分析: (1)按照user_id及create_date 分组求消费金额total_amount (2)开窗计算同user_id下的累计销售金额sum(total_amount) over(partition by user_id order by create_date ROWS BETWEEN UNBOUNDED PRECEDING AN…...
解决MySQL错误-this is incompatible with sql_mode=only_full_group_by
报错 Expression #1 of SELECT list is not in GROUP BY clause and contains nonaggregated column ‘数据库名.表名.字段名’ which is not functionally dependent on columns in GROUP BY clause; this is incompatible with sql_modeonly_full_group_by 原因 MySQL错误-t…...

UDP通信-广播、组播
UDP的三种通信方式 单播:单台主机与单台主机之间的通信。 广播:当前主机与所在网络中的所有主机通信。 组播:当前主机与选定的一组主机的通信。 UDP如何实现广播 使用广播地址:255.255.255.255 具体操作: 发送端…...

10-bean创建流程1一finishBeanFactoryInitialization(ConfigurableListableBeanFactory
文章目录 1. 方法的主要流程2. ConversionService-如何自定义转换器3. AbstractBeanFactory#getMergedLocalBeanDefinition(String beanName)4.FactoryBean实例化5.内置值处理器1. 方法的主要流程 /*** Finish the initialization of this contexts bean factory,* initializi…...
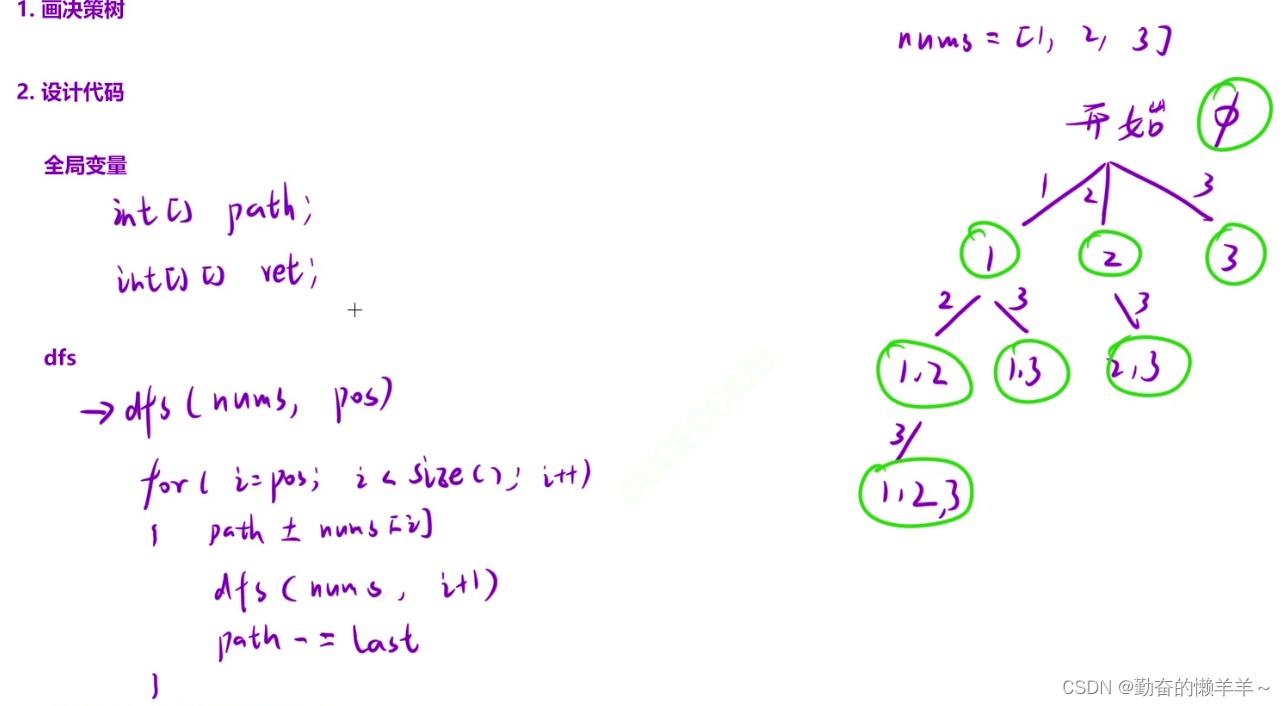
专题三:穷举、暴搜、深搜、回溯、剪枝【递归、搜索、回溯】
1、全排列 class Solution { public:vector<vector<int>> ret;vector<int> path;bool check[7];void dfs(vector<int>& nums){if(nums.size() path.size()) {ret.push_back(path);return;}for(int i 0;i < nums.size();i){if(check[i] fals…...

国科云SSL证书讲堂:SSL证书安装常见问题盘点
SSL证书能够对网站传输数据进行加密处理,有效提升网站的数据安全防护能力,逐渐被越来越多的政企网站所应用。但在安装使用SSL证书时,经常会发生各种意想不到的问题,对网站的数据安全和正常访问造成严重影响。本文国科云对安装使用…...
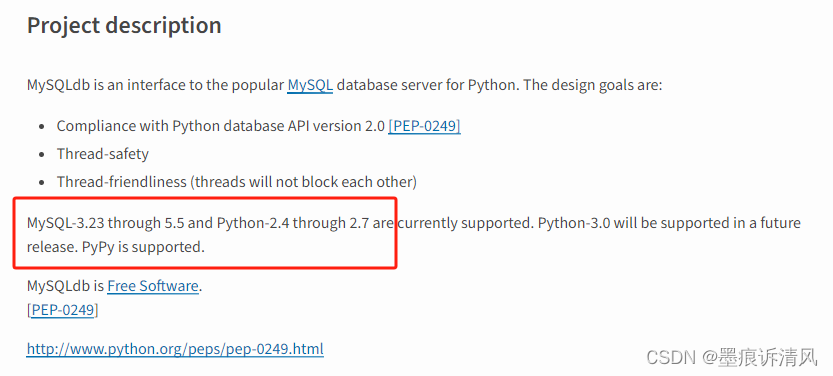
Python3无法调用Sqlalchemy解决(mysqldb)
原因 在安装Sqlalchemy后运行程序报错 无法导入mysqldb,缺失模块 ImportError: No module named ‘MySQLdb’ 既然缺少 MySQLdb 这个模块,尝试按照正常的想法执行 pip install MySQLdbpip install mysql-python 应该能解决,但是却找不到…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
