金融数学方法:梯度下降法
1.算法介绍
梯度下降法是一种常用的优化算法,其通过沿着梯度下降的方向迭代寻找局部极小值。如果沿着梯度上升的方向迭代,就可以找到极大值。
在梯度下降法中,我们首先需要选择一个初始点 x 0 x_0 x0作为起始位置,然后计算当前位置的梯度(即函数在该点的导数)。接着,我们根据梯度的反方向来更新当前位置,使得函数值逐渐减小,直到达到局部最小值或收敛。梯度下降法的更新公式为 x n + 1 = x n − λ n ∇ F ( x n ) (1) x_{n+1}=x_n-\lambda_n \nabla F(x_n) \tag{1} xn+1=xn−λn∇F(xn)(1)其中, λ n \lambda_n λn是步长, ∇ F \nabla F ∇F是函数的梯度。
我们需要考虑一个问题,那就是步长 λ n \lambda_n λn应该如何选取。如果步长太短,可能要迭代很多次,如果步长太长,可能会走过,错过极值点。我们可以先选择一个任意长度的步长,然后尝试着走,如果函数值下降了,则进行下一步迭代,如果函数值没有下降,那么就可以将步长取为现有的这一步,再次尝试,直到函数值下降为止,至于初始步长的选取,可以按照Barzilai-Borwein方法来定义
λ n = ∣ ( x n − x n − 1 ) T ( ∇ F ( x n ) − ∇ F ( x n − 1 ) ) ∣ ∣ ∣ ∇ F ( x n ) − ∇ F ( x n − 1 ) ∣ ∣ 2 (2) \lambda_{n}=\frac{\left|\left(x_{n}-x_{n-1}\right)^{\mathrm{T}}\left(\nabla F\left(x_{n}\right)-\nabla F\left(x_{n-1}\right)\right)\right|}{|| \nabla F\left(x_{n}\right)-\nabla F\left(x_{n-1}\right)||^{2}} \tag{2} λn=∣∣∇F(xn)−∇F(xn−1)∣∣2 (xn−xn−1)T(∇F(xn)−∇F(xn−1)) (2)
2.算例分析
用梯度下降法求 F ( x , y ) = ( x − 1 ) 2 + ( y − 1 ) 2 F(x,y)=(x-1)^2+(y-1)^2 F(x,y)=(x−1)2+(y−1)2的极小值。
首先求出函数F的梯度 ∇ F ( x , y ) = ( 2 ( x − 1 ) , 2 ( y − 1 ) ) \nabla F(x,y)=(2(x-1),2(y-1)) ∇F(x,y)=(2(x−1),2(y−1)),然后利用上面介绍的算法过程进行实现,以下是python实现代码。
def hanshu(x,y):return (x-1)*(x-1)+(y-1)*(y-1)
def daoshu(x,y):return [2*(x-1),2*(y-1)]
def calculate_lamb(x0,y0,d0,x1,y1,d1):f1=(x1-x0)*(d1[0]-d0[0])+(y1-y0)*(d1[1]-d1[0])f2=(d1[0]-d0[0])**2+(d1[1]-d0[1])**2return f1/f2
def grad_descent(x0,y0):f0=hanshu(x0,y0)d0=daoshu(x0,y0)i,lamb=0,0.01while i<1000:x1,y1=x0-lamb*d0[0],y0-lamb*d0[1]f1=hanshu(x1,y1)while f1>f0:lamb=lamb*0.5x1,y1=x0-lamb*d0[0],y0-lamb*d0[1]f1=hanshu(x1,y1)if (x1-x0)**2+(y1-y0)**2<0.000001:breakd1=daoshu(x1,y1)lamb=calculate_lamb(x0,y0,d0,x1,y1,d1)x0,y0,f0,d0=x1,y1,f1,d1i+=1return x1,y1,i
这里取初始值(10,10),代入算法中求得最优解为(1.000538330078125, 1.000538330078125),这个值就已经很接近理论最小值(1,1)啦!
需要注意的是,梯度下降法可能会陷入局部最小值而无法找到全局最小值,因此在实践中常常会根据需求使用其他优化算法。同时,通过调节迭代次数等超参数,可以对梯度下降法进行优化,以获得更好的结果。
相关文章:

金融数学方法:梯度下降法
1.算法介绍 梯度下降法是一种常用的优化算法,其通过沿着梯度下降的方向迭代寻找局部极小值。如果沿着梯度上升的方向迭代,就可以找到极大值。 在梯度下降法中,我们首先需要选择一个初始点 x 0 x_0 x0作为起始位置,然后计算当前位…...

1031 查验身份证
一.问题: 一个合法的身份证号码由17位地区、日期编号和顺序编号加1位校验码组成。校验码的计算规则如下: 首先对前17位数字加权求和,权重分配为:{7,9,10,5,8,4…...

如何共享 Android 不同模块的构建配置
最近想重新梳理学习一遍 Android 的各个知识点,于是新建了一个 AndroidStudy 项目仓库,打算每个知识块新建 1 个 module。 类似这样: AndroidStudy (Root Project) ├─app (Module0) ├─CustomView (Module1) ├─KotlinCoroutines (Modul…...
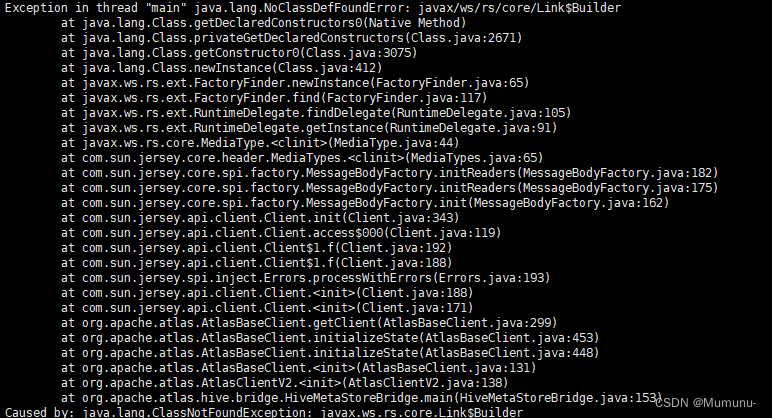
atlas运维中遇到的问题
1、java.lang.NoClassDefFoundError:javax/ws/rs/core/Link$Builder 主要原因:jsr311-api包中javax.ws.rs.core包中没有Link类,而Atlas以HBase作为元数据存储,HBase本身使用的为javax.ws.rs-api包中的core包,其中有Lin…...
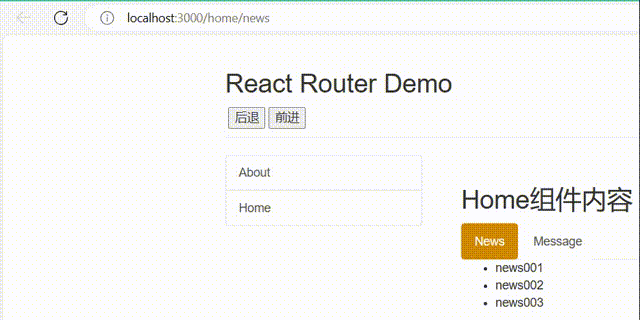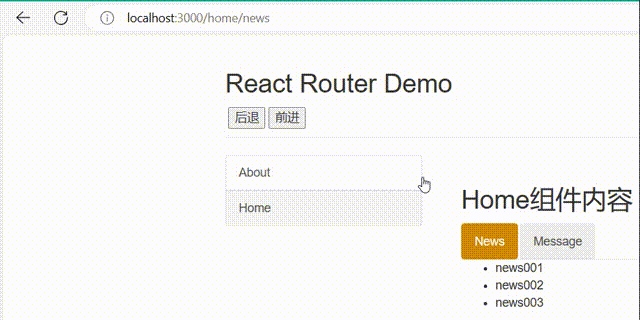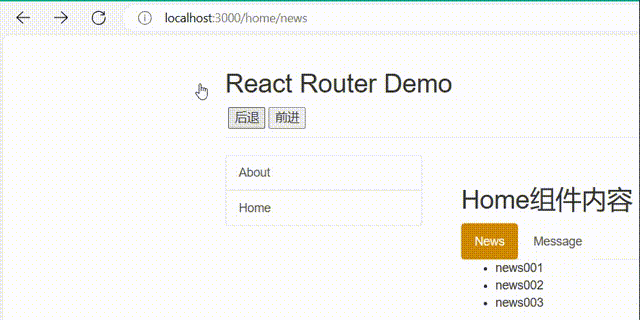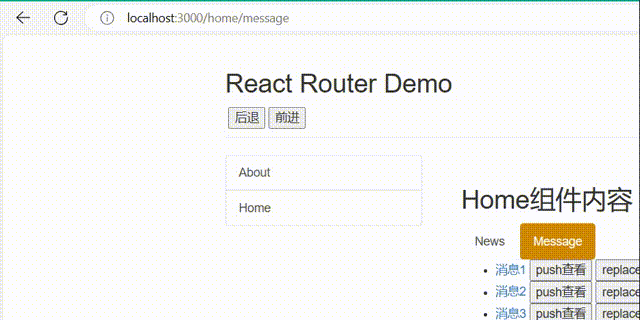
06-React的路由
06-React的路由 1.相关理解 1).SPA的理解 单页Web应用(single page web application,SPA)。整个应用只有一个完整的页面。点击页面中的链接不会刷新页面,只会做页面的局部更新。数据都需要通过ajax请求获取, 并在前端异步展现。…...
虹科方案 | 加州理工学院利用HK-TrueNAS开展地震研究
一、客户背景 加州理工学院(CalTech)是世界顶尖的理工类科学研究型学府之一。加州理工学院地震实验室是加州理工学院地质与行星科学部(GPS)的一个分支机构,成立于1921年,自20年代以来一直是世界地震学研究中心,并且几十年来一直是媒体对大地…...
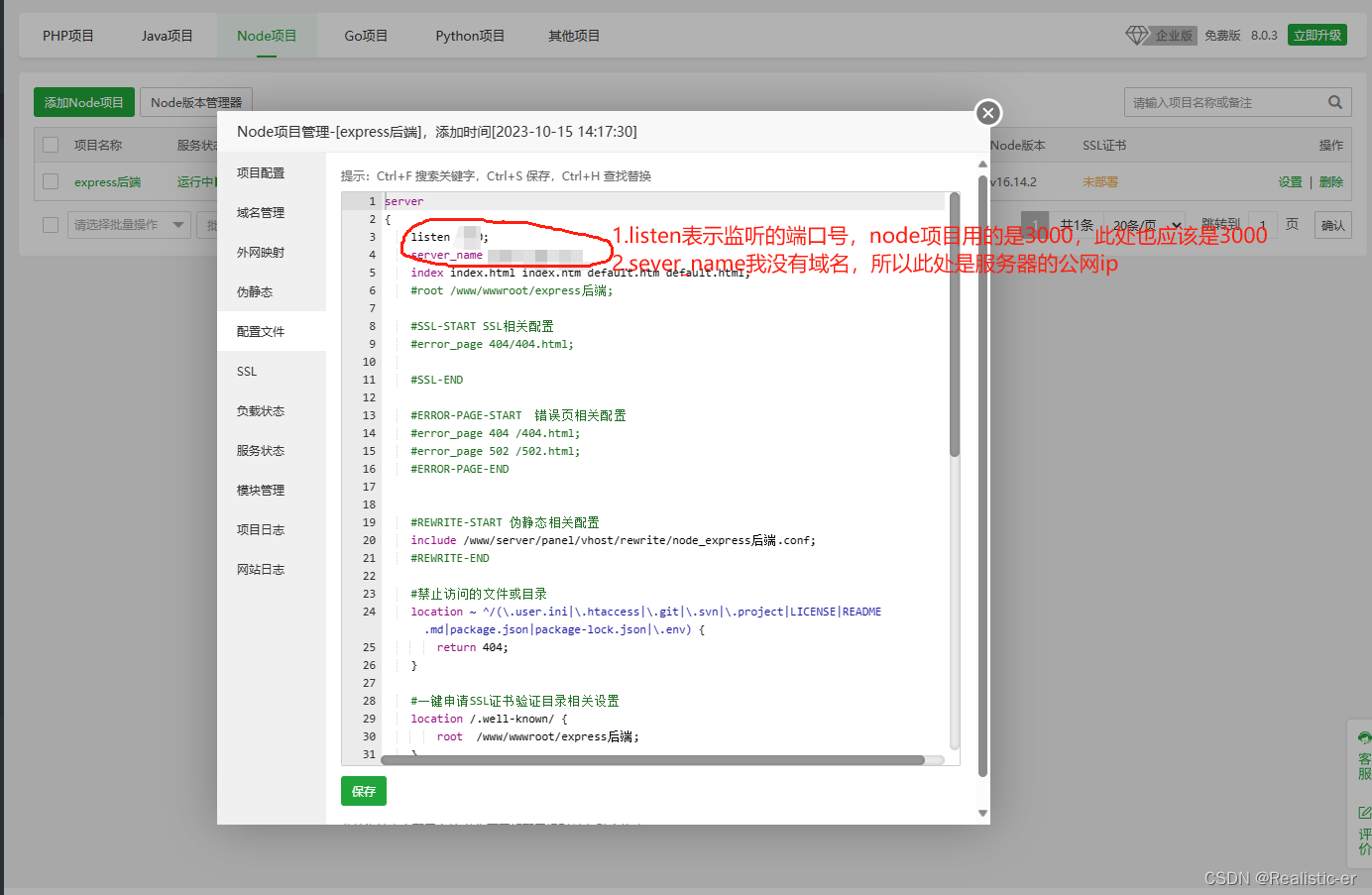
宝塔面板部署express以及MySql项目
第一次在宝塔面板上部署express和MySql项目,部署过程一直跑不通接口,特此记录一下。 在部署的时候,建议第一步把数据库MySql给跑通,中间好多原因是由于数据库的原因给引起的。 一.连接数据库 (1)在宝塔面…...
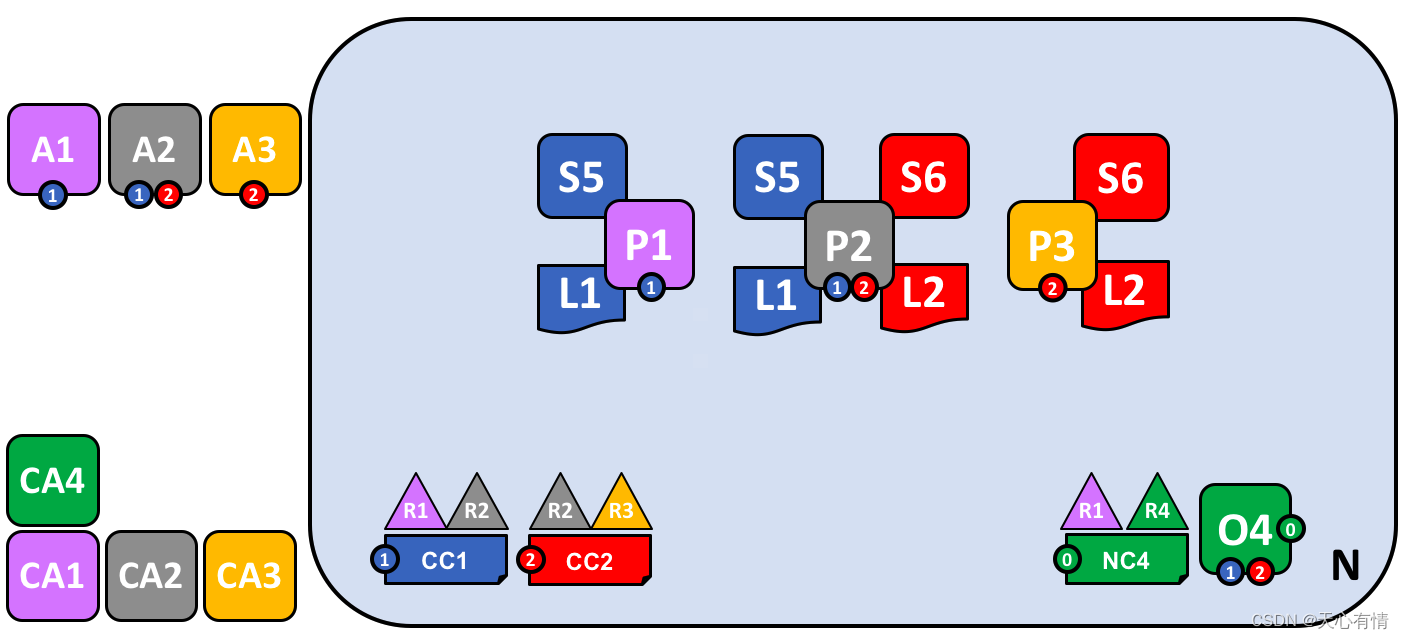
联盟链学习笔记-网络的创建
联盟链学习笔记 初始网络 下图是初始网络网络N的参考图 排序服务 在定义 网络 N 的时候,第一件事情就是定义一个 排序服务O4。O4 最初被配置并且由组织 R4 的一个管理员来启动,并且由 R4 管理。配置 NC4 包含了描述网络管理能力初始集合的规则。最初在…...

System.Drawing.Common.Bitmap跨平台的替代方案
使用SkiaSharp SkiaSharp是Skia Graphics Library的.Net跨平台实现,它可以在Windows,macOS,Linux,iOS,Android和其他平台上使用。 例如需要Linux版,则安装第一个和第四个: 以下是使用SkiaShar…...

深入理解 Java 泛型
没有泛型是怎样的 了解点 Java 历史的都知道,泛型是从 JDK 1.5 版本添加的特性,在 JDK1.5 之前,Java 很多特性都是没有的例如:泛型、注解、自动装箱和拆箱、可变参数。在介绍泛型之前,我们先来看看,如果没有泛型的世界是怎么样的。 假设有一个 List,我只想把 String 类…...
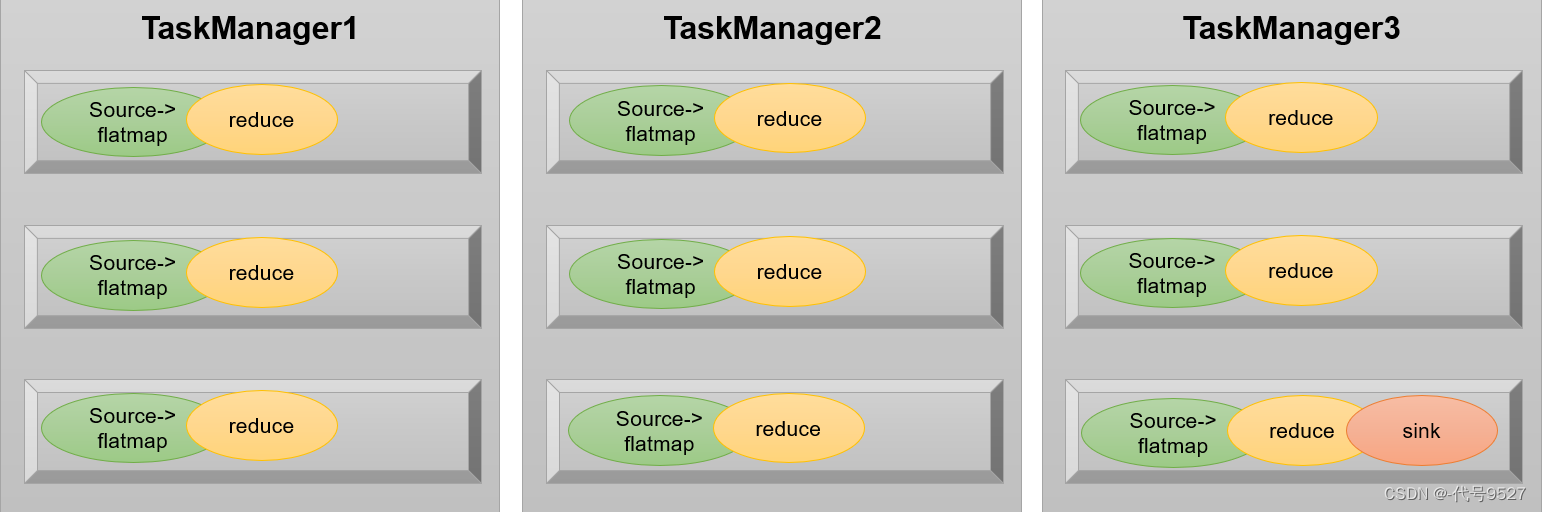
【基础篇】七、Flink核心概念
文章目录 1、并行度2、并行度的设置3、算子链4、禁用算子链5、任务槽6、任务槽和并行度的关系 1、并行度 要处理的数据量很多时,可以把一个算子的操作(比如前面demo里的flatMap、sum),"复制"多份到多个节点,…...

06-Scala面向对象
面向对象编程 Scala是一门完全面向对象的语言,摒弃了Java中很多不是面向对象的语法。 虽然如此,但其面向对象思想和 Java的面向对象思想还是一致的 Scala包 1)基本语法 Scala中基本的package包语法和 Java 完全一致 例如…...
【设计模式】单例模式、“多例模式”的实现以及对单例的一些思考
文章目录 1.概述2.单例模式实现代码2.1.饿汉式单例2.2.懒汉式单例2.3.双检锁单例2.4.静态内部类单例2.5.枚举单例 3.对单例的一些思考3.1.是否需要严格的禁止单例被破坏?3.2.懒汉式真的比饿汉式更佳吗?3.3.单例存在的问题 4.其他作用范围的单例模式4.1.线…...
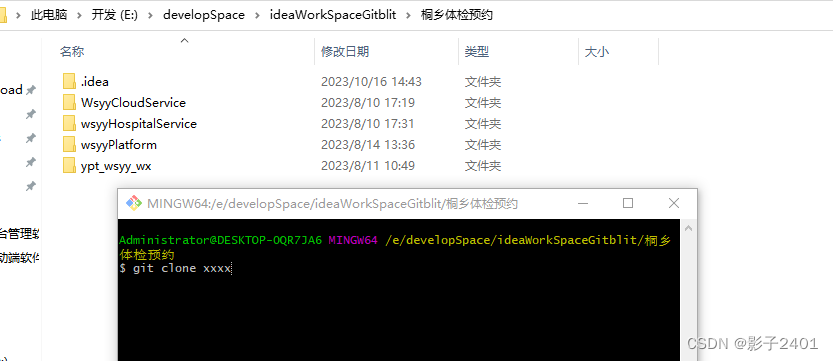
idea 2022 一个工作空间下导入git项目 后 无法导入第二个git项目
idea 2022 一个工作空间下导入git项目 后 无法导入第二个git项目 如图所示 我导入了一个git项目后,菜单栏出现了一个git按钮 找不到 导入git项目的按钮了 方式1、 通过idea设置 打开全局设置 如下图 把git先改为none,保存 保存后就可以看到 VCS按钮 导入…...

泛在电力物联网的关键技术与未来发展策略-安科瑞黄安南
摘要: 文章分析了泛在电力物联网的内涵及其主要特征,针对泛在电力物联网的建设目标、基本构架以及关键技术与未来发展策略进行综合探讨,期待得到专业人士的指点。 关键词: 泛在电力物联网, 网络规划, 网络发展 随着能源革命的不…...
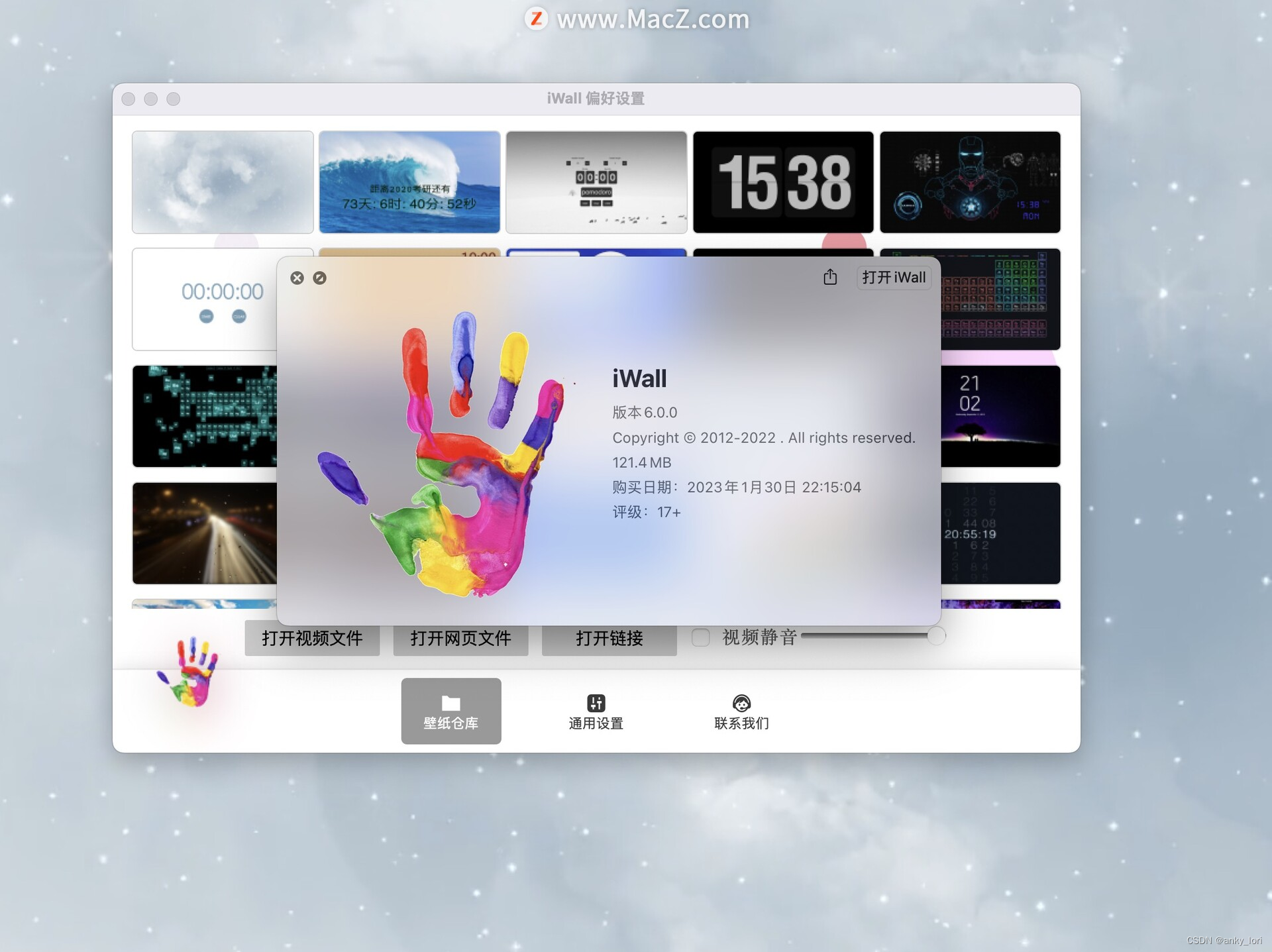
iWall:支持自定义的Mac动态壁纸软件
iWall Mac是一款动态壁纸软件,它可以使用任何格式的漂亮视频(无须转换)、图片、动画、Flash、gif、swf、程序、网页、网站做为您的动态壁纸、动态桌面,并且可以进行交互。 这款软件功能多、使用简单、体积小巧、不占用资源、运行…...

【Docker 内核详解】namespace 资源隔离(四):Mount namespace Network namespace
【Docker 内核详解 - namespace 资源隔离】系列包含: namespace 资源隔离(一):进行 namespace API 操作的 4 种方式namespace 资源隔离(二):UTS namespace & IPC namespacenamespace 资源隔…...

STM32简介
STM32是ST公司基于ARM Cortex-M内核开发的32位微控制器,常应用在嵌入式领域如: 智能车(用stm32做寻迹小车,读取光电传感器或者摄像头数据,然后驱动电机前进和转弯); 无人机(用stm3…...

Yum安装JDK11
一、安装命令 : yum install java-11-openjdk二、执行以下命令来查看 JDK 11 的安装信息: yum list installed | grep java-11-openjdk三、找到 JDK 11 的软件包名称(使用以下命令来查询软件包的安装位置): rpm -ql…...
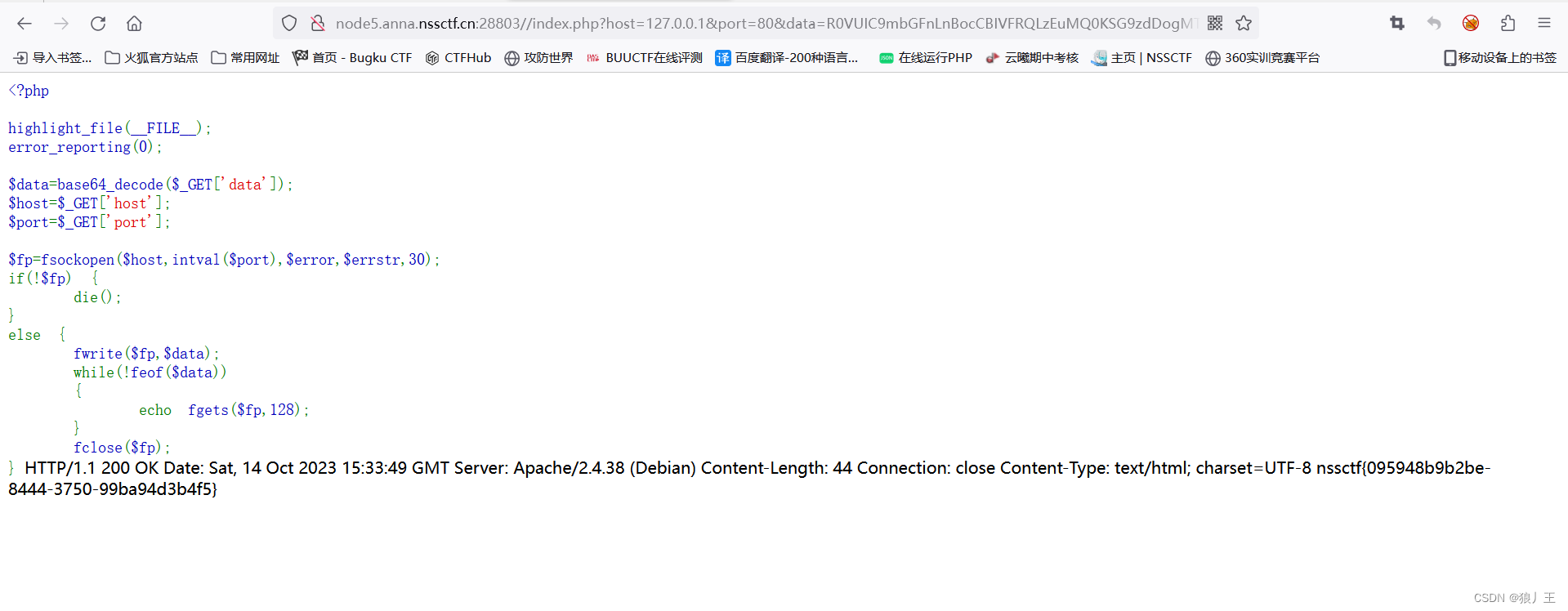
[HNCTF 2022 WEEK2]ez_ssrf题目解析
这题主要是引入ssrf这个漏洞攻击,本质上没有更深入的考察 本题是需要我们去伪造一个ssrf的请求头去绕过 题目开始给了我们信息让我们去访问index.php fsockopen函数触发ssrf fsockopen() 函数建立与指定主机和端口的 socket 连接。然后,它将传入的 bas…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
