LeetCode 2652. 倍数求和【数学,容斥原理】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个正整数 n ,请你计算在 [1,n] 范围内能被 3、5、7 整除的所有整数之和。
返回一个整数,用于表示给定范围内所有满足约束条件的数字之和。
示例 1:
输入:n = 7
输出:21
解释:在 [1, 7] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7 。数字之和为 21 。
示例 2:
输入:n = 10
输出:40
解释:在 [1, 10] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7、9、10 。数字之和为 40 。
示例 3:
输入:n = 9
输出:30
解释:在 [1, 9] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7、9 。数字之和为 30 。
提示:
1 <= n <= 10^3
解法 容斥原理
在 [ 1 , n ] [1,n] [1,n] 中, m m m 的倍数有 k = ⌊ n m ⌋ k = \left\lfloor\dfrac{n}{m}\right\rfloor k=⌊mn⌋ 个,即
m , 2 m , ⋯ , k m m,2m,\cdots,km m,2m,⋯,km
结合等差数列求和公式,这些数的和为
s ( m ) = k ( k + 1 ) 2 ⋅ m s(m) = \dfrac{k(k+1)}{2} \cdot m s(m)=2k(k+1)⋅m
再结合容斥原理,可以算出 3 3 3 或 5 5 5 或 7 7 7 的倍数之和,即
s ( 3 ) + s ( 5 ) + s ( 7 ) − s ( 15 ) − s ( 21 ) − s ( 35 ) + s ( 105 ) s(3) + s(5) + s(7) - s(15) - s(21) - s(35) + s(105) s(3)+s(5)+s(7)−s(15)−s(21)−s(35)+s(105)
class Solution {
private:int s(int n, int m) {return n / m * (n / m + 1) / 2 * m; // n/m=k,说明[1,n]中为m倍数的数有k个}
public:int sumOfMultiples(int n) {return s(n, 3) + s(n, 5) + s(n, 7) - s(n, 15) - s(n, 21) - s(n, 35) + s(n, 105);}
};
相关文章:

LeetCode 2652. 倍数求和【数学,容斥原理】简单
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

ansible-playbook剧本
一,playbook组成: (1)Tasks:任务,即通过 task 调用 ansible 的模板将多个操作组织在一个 playbook 中运行 (2)Variables:变量 (3)Templates&…...
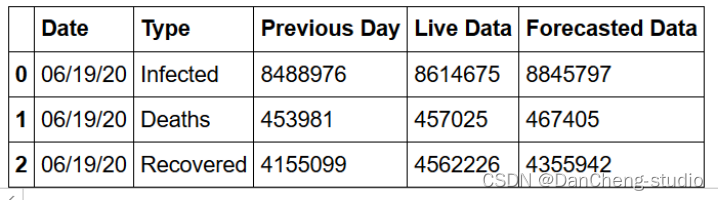
竞赛选题 深度学习LSTM新冠数据预测
文章目录 0 前言1 课题简介2 预测算法2.1 Logistic回归模型2.2 基于动力学SEIR模型改进的SEITR模型2.3 LSTM神经网络模型 3 预测效果3.1 Logistic回归模型3.2 SEITR模型3.3 LSTM神经网络模型 4 结论5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 …...

机械设计师应该在工作中培养哪些良好习惯?
图纸规范 1、一定要按照制图标准设计图纸!图纸上任何一条直线(无论是点划线、粗实线、细实线等等)、数值、公差、图标等,都必须有理有据,不能想当然。图纸是产品生产的基础,无论是生产、加工、装配&#x…...

小程序新增功能页面
需求背景: 小程序主页面有个报名板块,我打算替换主页面报名板块菜单,迁移到我的页面里面, 替换成资讯栏目,我喜欢分享最新技术,开源课题,IT资讯,本想做成论坛的效果,由于时间问题,先替换添加板块 替换后效果: 模块功能: 添加、修改、删除、查看 文件目录:// 添…...

LeetCode每日一题——2652. Sum Multiples
文章目录 一、题目二、题解 一、题目 Given a positive integer n, find the sum of all integers in the range [1, n] inclusive that are divisible by 3, 5, or 7. Return an integer denoting the sum of all numbers in the given range satisfying the constraint. E…...
)
Python问答题(更新中)
1. 列表(list)和元组(tuple)有什么区别? 列表是可变的,创建后可以对其进行修改;元组是不可变的,元组一旦创建,就不能对其进行更改。列表表示的是顺序。它们是有序序列&a…...

服务器中了locked勒索病毒怎么办,勒索病毒解密,数据恢复
最近一段时间内,相信很多使用金蝶或用友的办公软件的企业,有很多都经历了locked勒索病毒的攻击,导致企业服务器被加密无法正常使用,严重影响了企业的正常工作。通过云天数据恢复中心的解密恢复发现,在今年locked勒索病…...

游游的字母串 (环形数组两点之间的位置)
题目链接:登录—专业IT笔试面试备考平台_牛客网 题目: 样例: 输入 yab 输出 3 思路: 暴力枚举,全部变成对应的26个字母字符需要的操作步数,取最少的一个操作步数, 这里的操作步数࿰…...
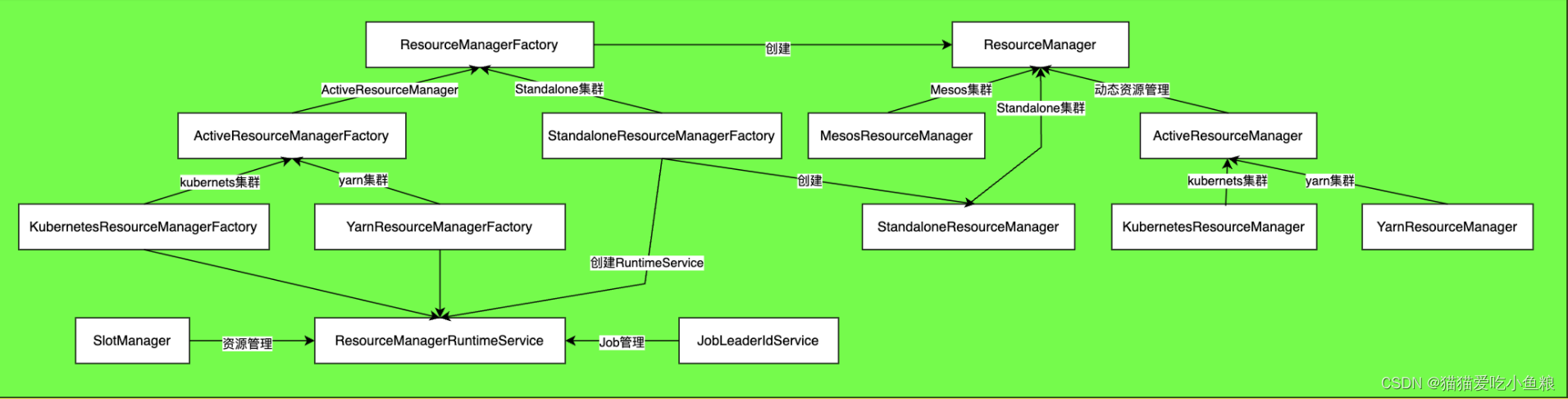
Flink的ResourceManager详解(一)
ResourceManager 总结 一、概述 1、ResourceManager 管理 Flink 集群中的计算资源,计算资源主要来自 TaskManager 组件。 2、如果集群采用 Native【本地模式】部署,则 ResourceManager 会动态地向集群资源管理器申请 Container 并启动TaskManager&…...

Tornado 可以使用 nginx 提供负载均衡
Tornado和nginx都是网络服务器的重要组成部分,但它们在职能和使用场景上存在显著的差异。 Tornado可以独立运行,而不需要依赖nginx等其他Web服务器。这是因为Tornado本身就是一个完整的Web服务器,可以独立处理HTTP请求并返回响应数据。 ngi…...

Golang 面向对象编程 多态
基本介绍 变量(实例)具有多种形态。面向对象的第三大特征,在Go语言,多态特征是通过接口实现的(接口能够体现多态的特征)。可以按照统一的接口来调用不同的实现。这时接口变量就呈现不同的形态。 在前面的Usb接口案例,u…...

WLAN 无线案例(华为AC控制器配置模板)
实验说明: 无线用户VLAN 30 192.168.30.0/24 AP和AC用VLAN 20 192.168.20.0/24 有线网段 VLAN 10 192.168.10.0/24 步骤一:全网互通 sw1: sysname sw1 # vlan batch 10 20 30 # dhcp enable # ip pool 20 gateway-list 192.168.20.1…...

精美的早安问候语,暖心祝福,开心每一天
1、 美好的祝福,成了清晨的主题。相互问候,是一天的开始。让我们伴着不老的岁月,永远开心快乐。早晨好! 2、 心宽似海,百福皆来,世事看淡,内心安然。随缘即福,随遇而安࿰…...
嵌入式养成计划-41----C++ auto--lambda表达式--C++中的数据类型转换--C++标准模板库(STL)--list--C++文件操作
九十九、auto 99.1 概念 C11引入了自动类型推导,和Python不一样,C中的自动类型推导,需要auto关键字来引导比如 :auto a 1.2; 会被编译器自动识别为 a 为 double 类型 99.2 作用 auto修饰变量,可以自动推导变量的数…...
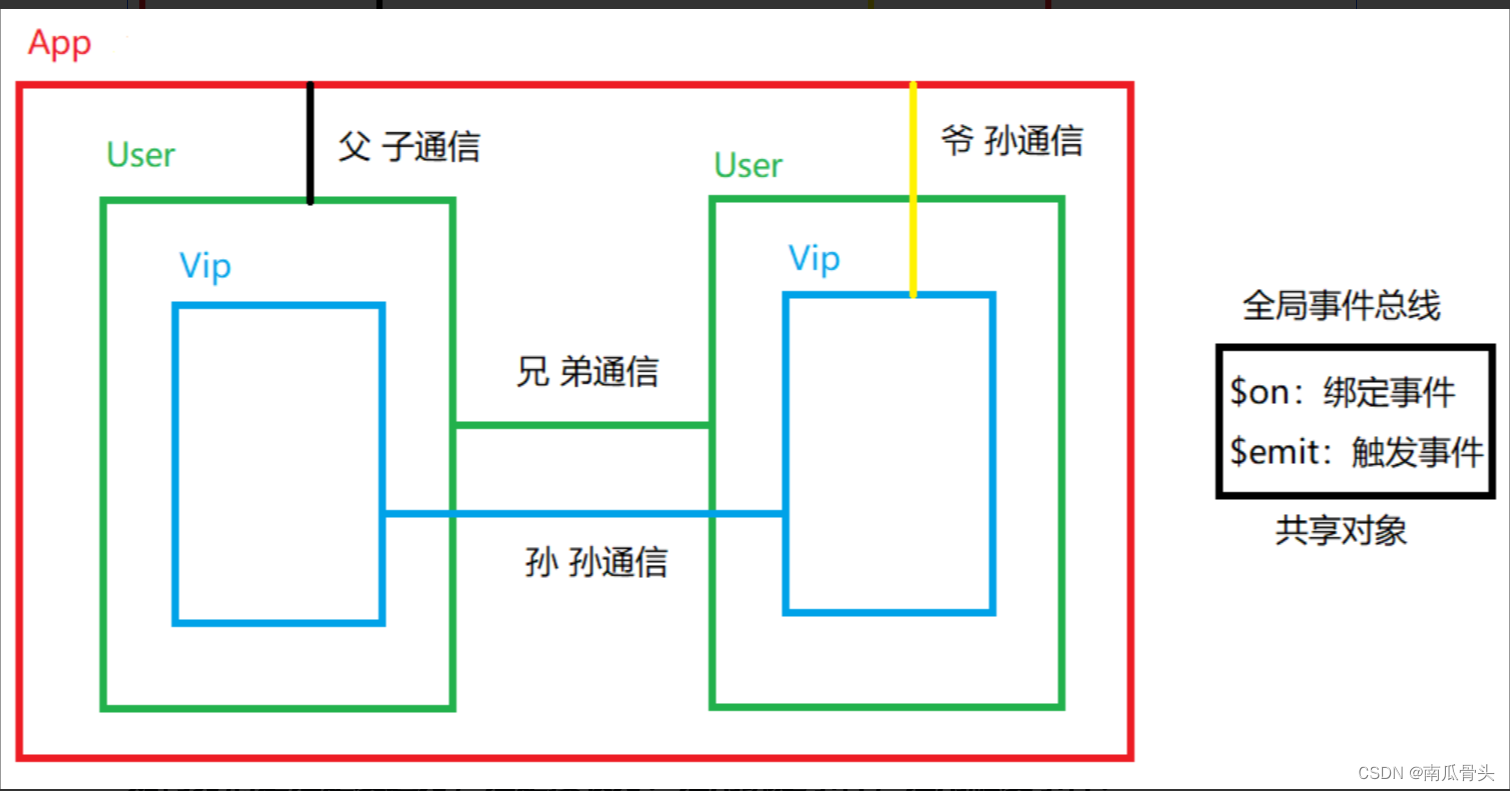
全局事件总线
全局事件总线 功能:可以解决所有组件之间通信传数据的问题原理:通过一个共享对象,将所有组件全部绑定到对象上,即可通过这个对象实现组件与组件之间的传递数据,而这个共享对象叫做全局事件总线。 如何分清楚谁是发送方…...

通讯网关软件026——利用CommGate X2ORACLE-U实现OPC UA数据转入ORACLE
本文介绍利用CommGate X2ORACLE-U实将OPC UA数据源中的数据转入到ORACLE数据库。CommGate X2ORACLE-U是宁波科安网信开发的网关软件,软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示,将OPC UA数据源的数据写入到ORACLE数据…...

RAII与智能指针
RAII与智能指针 1.RAII1.1RAII理解1.2RAII的原理1.2.1简单的例子说明局部对象的自动销毁的特性 1.2.2 RAII 过程 2.智能指针2.1 auto_ptr2.1.1auto_ptr的使用构造函数与析构函数拷贝构造函数与赋值提领操作auto ptr其它函数 2.1.2autoptr使用的注意事项 2.2 unique_ptr2.2.1uni…...

易云维智慧工业云平台助力广西国企培育数字产业化平台,打造数字化产业生态
2022年6月6日,广西壮族自治区人民政府国有资产监督管理委员会出台了《国有企业数字化转型工作实施意见》,明确了总体要求、主要目标、重点推进国有企业数字化转型的任务和保障措施。 《意见》预计,到2025年底,广西基本实现自治区级…...
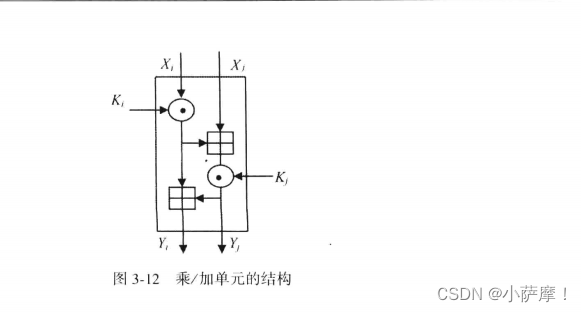
【密码学】第三章、分组密码
DES、IDEA、AES、SM4 1、分组密码定义(按照五个组成部分答) 密钥空间:属于对称加密算法kekd明密文空间:将明文划分为m比特的组,每一块依次进行加密加解密算法:由key决定一个明文到密文的可逆映射 2、发展…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
