面试准备-深入理解计算机系统-信息的表示与处理1
浮点运算是不可结合的(由于表示的精度有限)。比如(3.14+1e20)-1e20是0.0而3.14+(1e20-1e20)是3.14。整数虽然只能编码一个较小的取值范围,但是是准确的;浮点数虽然能编码更大的范围,但是是近似的。
二进制转十六进制转换技巧1
如果x = 2^n,且n = i + 4j,i∈[0, 3],那么可以将x写成 i’后跟j个0。其中i=0, i’=1; i=1, i’= 2
i = 2, i’=4; i = 3, i’=8 (记忆:0001,0010,0100,1000,i表示后面0的个数)
举例:
x = 2048 = 2^11,此时n = 11 = 3 + 4 * 2,则i=3, j=2,那么写成16进制为0x800
总线:负责以定长字节块的形式传递信息。定长字节块就是字word,其字节数就是字长word size。
对于一个字长为w位的机器而言,虚拟地址的范围是0~2^w - 1,程序最多访问2^w个字节。因此,字长决定了虚拟地址空间的最大大小。
32位字长=虚拟地址空间4GB
64位机器可以运行32位机器编译的程序,这是一种向后兼容
linux> gcc -m32 xx.c
linux> gcc -m64 xx.c
前者可以在32/64位机器上运行,后者则只能在64位运行。
大端和小端是一个对象所有字节的存储方式。假设一个变量x是int型,位于地址0x100处,十六进制值为0x01234567,那么地址范围0x100~0x103的字节顺序依赖于机器。一般选择了os,字节顺序救固定了。如果使用ASCII码,字符串在任何机器都是一样的结果(不看大小端),所以str比二进制数据更具有平台独立性。
大端big endian
| 0x100 | 0x101 | 0x102 | 0x103 | ||
|---|---|---|---|---|---|
| …… | 01 | 23 | 45 | 67 | …… |
小端little endian
| 0x100 | 0x101 | 0x102 | 0x103 | ||
|---|---|---|---|---|---|
| …… | 67 | 45 | 23 | 01 | …… |
ASCII码适合英语文档,增加其他字母之后有了Unicode(使用4个字节编码)。UTF-8包含ASCII,每个字符用1个字节编码。Java使用Unicode表示字符串,C也有支持Unicode的库。
位运算
^ XOR,exclusive-OR,异或
布尔&对|,|对&都有分配律:
a & (b | c) = (a & b) | (a & c)
a | (b & c) = (a | b) & (a | c)
加法逆元additive inverse : x + (-x) = 0,那么-x就是x的加法逆元
a ^ a = 0 → (a ^ b) ^ a = b
C语言逻辑运算符|| && !认为非0参数都是True(1),0是False(0)。同时,如果第一个参数就能确定表达式的结果,就不会对第二个参数求值。
x>>k 右移包括两种:逻辑右移和算术右移。前者左端要补k个0,后者是左端补k个最高有效位的值。比如x = 0110 0011,x >> 4(算术右移)= 0000 0110;x = 1001 0101 → 1111 1001
对C来说几乎所有的编译器、机器都会对有符号数使用算术右移,对于无符号数,右移必须是逻辑右移。Java则规定>>是算术右移,>>>是逻辑右移。
位移的优先级低于+
整数表示
机器规定的各种数据类型的取值范围不是对称的,负数比正数的范围大1。但是C语言的规定某些是对称的(char short int)。而且C可以用2个字节实现int。C和C++支持有符号(默认)和无符号数,但Java只支持有符号数。
对向量 x ⃗ = [ x w − 1 , x w − 2 , . . . , x 0 ] , B 2 T w ( x ⃗ ) = − x w − 1 2 w − 1 + ∑ i = 0 w − 2 x i 2 i 对向量\vec{x}=[x_{w-1}, x_{w-2}, ..., x_0], B2T_w(\vec{x})=-x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_i2^i 对向量x=[xw−1,xw−2,...,x0],B2Tw(x)=−xw−12w−1+i=0∑w−2xi2i
补码: two’s-complement。最高有效位称为符号位,解释为负权negative weight(-2^(w-1)),也就是说,这个最高位是1表示值为负。举例:
B2T4([0101]) = 5, B2T4([1101]) = -8 + 4 + 1 = -3
因此,w位有符号数,最大值应该是2(w-1)-1,最小值是-2(w-1)。举例:对于4位有符号数,最大值应该是0111(符号位是0,剩余都是1),也就是7;最小值应该是(符号位为1,剩余都是0,这样不会有加值),也就是-8。这就是机器规定的有符号数的取值范围是不对称的原因。
| 数 | 字长w | |
|---|---|---|
| U是无符号 | 8 | 16 |
| UMax | 0xFF 255 | 0xFFFF 65535 |
| TMin | 0x80 -128 | 0x8000 -32768 |
| TMax | 0x7F 127 | 0x7FFF 32767 |
| -1 | 0xFF | 0xFFFF |
| 0 | 0x00 | 0x0000 |
注意:
1)-1和UMax是一样的,都是全1串
2)UMax = 2TMax + 1
反码:One’s Complement,除了最高有效位的权是 − ( 2 w − 1 − 1 ) -(2^{w-1}-1) −(2w−1−1)外,与补码一样。反码的来源是,用[111…1]-x来计算-x的反码表示,其实也就是直接按位反转。例如:
0101 = 5,w=4,则-5 = 1111 - 0101 =1010 = -1x(2^3-1)+2=-5
B 2 O w ( x ⃗ ) = − x w − 1 ( 2 w − 1 − 1 ) + ∑ i = 0 w − 2 x i 2 i B2O_w(\vec{x})=-x_{w-1}(2^{w-1}-1)+\sum_{i=0}^{w-2}x_i2^i B2Ow(x)=−xw−1(2w−1−1)+i=0∑w−2xi2i
原码:Sign-Magnitude,最高有效位是符号位,不参与计算,用剩下的位计算值
B 2 S w ( x ⃗ ) = ( − 1 ) x w − 1 ⋅ ( ∑ i = 0 w − 2 x i 2 i ) B2S_w(\vec{x})=(-1)^{x_{w-1}}\cdot(\sum_{i=0}^{w-2}x_i2^i) B2Sw(x)=(−1)xw−1⋅(i=0∑w−2xi2i)
需要注意的是,几乎所有现代机器都使用补码。
而且这两种表示方法中,[000…0]都是+0,但反码中,[111…1]表示为-0;在源码中,[10…0]表示为-0,所以对于0都是由两种表示方式的。
C语言实现数据类型的强制转换时,是改变了解释位的方式。
补码转无符号数
T 2 U w ( x ) = { x + 2 w , x < 0 x , x ≥ 0 } T2U_w(x)=\left\{\begin{aligned}x+2^w, x<0\\x, x\geq0\end{aligned}\right\} T2Uw(x)={x+2w,x<0x,x≥0},其中w是字长
相关文章:

面试准备-深入理解计算机系统-信息的表示与处理1
浮点运算是不可结合的(由于表示的精度有限)。比如(3.141e20)-1e20是0.0而3.14(1e20-1e20)是3.14。整数虽然只能编码一个较小的取值范围,但是是准确的;浮点数虽然能编码更大的范围,但是是近似的。 二进制转十六进制转换…...

搭建Atlas2.2.0 集成CDH6.3.2 生产环境+kerberos
首先确保环境的干净,如果之前有安装过清理掉相关残留 确保安装atlas的服务器有足够的内存(至少16G),有必要的hadoop角色 HDFS客户端 — 检索和更新Hadoop使用的用户组信息(UGI)中帐户成员资格的信息。对调…...
【运维笔记】swow源码编译安装
swow的github网址 https://github.com/swow/swow 从github中拉取源码 git pull https://github.com/swow/swow.git 编译安装 github中readme文件讲述了安装方法 这里整理了命令,进入拉取项目的目录后依次执行命令即可 #pwd 确保自己在swow目录中,如…...

【2023/10/16 下午10:32:39】
2023/10/16 下午10:32:39 BOOL Create(LPCTSTR strTitle, DWORD dwStyle, const RECT &rect, CWnd *pwndParent, DWORD dwPaletteSetStyle = PSS_PROPERTIES_MENU | PSS_AUTO_ROLLUP | PSS_CLOSE_BUTTON | PSS_SNAP); 2023/10/16 下午10:32:46 这是一个函数声明,看起来…...
qemu基础篇——VSCode 配置 GDB 调试
文章目录 VSCode 配置 GDB 调试安装 VSCode 插件调试文件创建调试配置配置脚本qemu 启动脚 启动调试报错情况一报错情况二报错情况三 调试界面运行 GDB 命令查看反汇编断点查看内核寄存器查看变量参考链接 VSCode 配置 GDB 调试 qemu-基础篇——arm 裸机调试环境搭建 上一节中…...

Spark常用算子
转换算子 value类型 算子名称作用Map映射a->bflatMap扁平化[[a,b],[c,d]] -> [a,b,c,d] ,二维变一维groupBy分组[1,2,3,4] ->[[1,3],[2,4] ],一维变二维filter过滤[1,2,3,4] -> [2,4] 符合条件进入,不符合去掉distinct去重[1,1…...
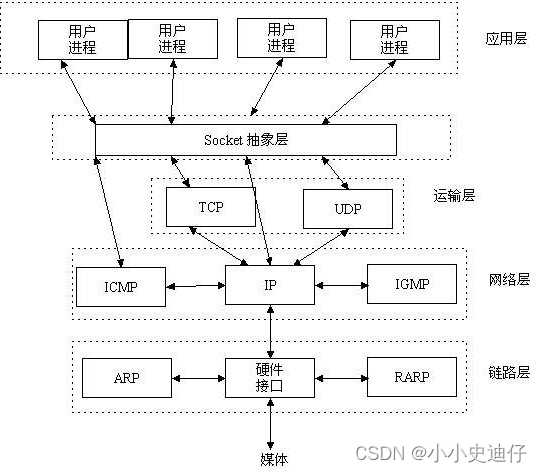
day35
今日内容概要 Socket抽象层(socket编程) 基于TCP协议的借助socket可以编程客户端和服务端的程序 链接循环 通信循环 基于UDP协议的套接字(socket)编程 粘包现象 如何解决粘包现象(重要的是解决的思路) struct模块的使用(打包、解包) 今日内容详细 Socket抽象层&#x…...

js原型链以及实现继承的手段
1.原型链 其基本思想是利用原型让一个引用类型继承另一个引用类型的属性和方法。 简单回顾一下构造函数、原型和实例的关系:每个构造函数都有一个原型对象,原型对象都包含一个指向构造函数的指针,而实例都包含一个指向原型对象的内部指针。…...

jdk8u201版本cpu.load过高问题的排查和解决
文章目录 1、背景2、现象3、排查定位4、原因总结5、解决 1、背景 jdk8u45版本存在安全漏洞,性能问题。需要升级到8u201 2、现象 升级到201版本后,出现cpu.load过高 3、排查定位 使用压测工具压测时,cpu.load过高问题必现,确认…...
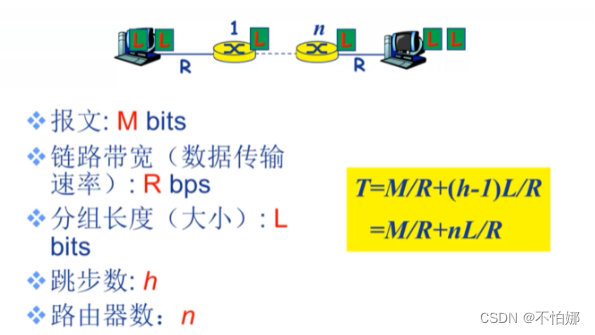
【计算机网络笔记】数据交换之报文交换和分组交换
系列文章目录报文交换分组交换存储-转发报文交换 vs 分组交换总结 系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 报文交换 报文:源(应用)发送的信息整体。比如一个文件、一…...

【广州华锐互动】利用VR开展细胞基础实验教学有什么好处?
在科技发展的驱动下,虚拟现实(VR)技术已被广泛应用于各个领域,包括教育和医学。尤其是在医学教育中,VR技术已成为一种革新传统教学模式的有效工具。本文将探讨使用VR进行细胞基础实验教学的优势。 首先,VR技…...
基于SSM+Vue的咖啡销售系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

L2-026 小字辈
本题给定一个庞大家族的家谱,要请你给出最小一辈的名单。 输入格式: 输入在第一行给出家族人口总数 N(不超过 100 000 的正整数) —— 简单起见,我们把家族成员从 1 到 N 编号。随后第二行给出 N 个编号,…...

linux 查看系统版本
命令:lsb_release -a 可能遇到的问题: 问题1: 报错:command not found: lsb_release原因:系统没有安装 lsb_release解决方案:sudo apt-get install lsb-release 问题2: 报错: Tra…...
Python实现PDF转换文件格式
最近工作中经常遇到收到其他人提供的pdf文档,想要编辑修改下或者复制部分内容比较困难,想通过现有的pdf工具软件转换文档格式,基本都要充钱,为了免费实现pdf转换工具,网上查了下相关技术方案,整理了下代码&…...

【Ceph Cluster】完全删除Ceph集群
注意:在执行这些步骤之前,请确保你已经备份了所有重要的数据,并且你明白这些步骤将永久删除 Ceph 集群。 停止 Ceph 服务: systemctl stop ceph.target卸载 Ceph 包:卸载 Ceph 相关的软件包,使用你的 Linux…...

4.Vue-Vue调用第三方接口
题记 用vue调用第三方接口,以下是全部代码和操作流程。 寻找第三方接口网站 推荐:免费API - 提供免费接口调用平台 (aa1.cn) 下面的代码以下图中的接口为例 安装axios模块 在终端输入以下命令: npm install axios 调用第三方接口代码 调…...

大语言模型在推荐系统的实践应用
本文从应用视角出发,尝试把大语言模型中的一些长处放在推荐系统中。 01 背景和问题 传统的推荐模型网络参数效果较小(不包括embedding参数),训练和推理的时间、空间开销较小,也能充分利用用户-物品的协同信号。但是它的缺陷是只能利用数据…...

第三章 交换技术及应用
目录 3.1 port-vlan技术 3.1.1 VLAN概述 3.1.2 VLAN划分方法——Port-VLAN 3.1.3 Port-VLAN工作原理 3.1.3 Port-VLAN配置 3.2 port-vlan仿真演示 3.2.1 实验背景 3.2.2 实验目的 3.2.3 实验设备 3.2.4 实验步骤思维导图 3.3 tag-vlan技术 3.3.1 问题分析 3.3.2 T…...
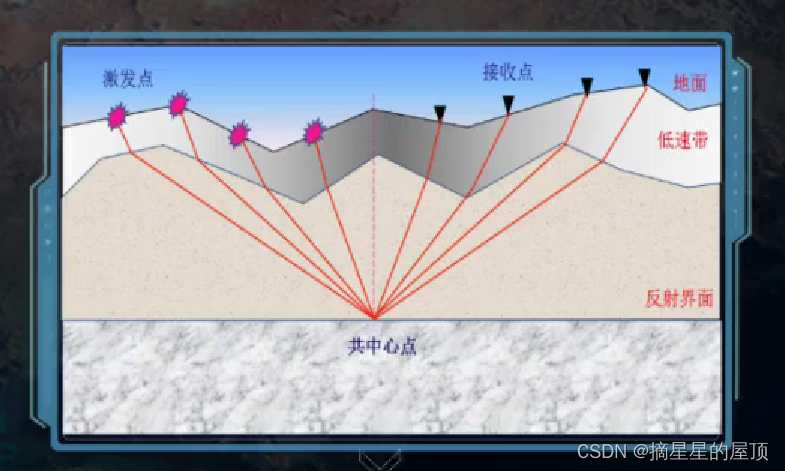
地震勘探原理部分问题解答
1、二维/三维(陆地/海洋)地震勘探,炮点(激发点)和检波点(接收点)的排布位置如何?画图作答? (1)陆地地震勘探 二维陆地地震野外采集:震…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
