实例8:机器人的空间描述和变换仿真
实例8:机器人的空间描述和变换仿真
实验目的
- 通过刚体与刚体的平动、转动基础知识的学习,熟悉位姿的描述
- 通过Python编程实践,可视化学习坐标系的变换,熟悉空间变换
实验要求
通过python编程,输入一指定向量和对应的绕行角度,使之在参考坐标系内绕x、y、z轴旋转指定角度,并依次按红、橙、绿、蓝绘制出原向量和绕x、y、z轴旋转后的向量
实验知识
1.实例介绍
在这个实例中,我们将学习机器人运动学的基础-空间的描述与变换。
空间的描述与变换将定性定量地解释四足机器狗上零件的基本运动,四足机器狗mini pupper上有12个舵机,每个舵机都有自己的空间位置和运动,为了表达舵机等零件的本身的位置和姿态,我们需要定义坐标系并给出表示的规则,这些位置和姿态的描述将作为表达线速度、角速度、力和力矩的基础。
为了描述空间中物体的位置和姿态,一般可以在物体上设置一个坐标系,称为物体坐标系,在参考坐标系中描述通过位置和姿态来描述这个物体坐标系。任一的坐标系也可以作为另一个坐标系的参考坐标系,这就涉及到了坐标系和坐标系之间的位置和姿态的变换,称之为位姿变换。因此,要了解mini pupper的运动,需要研究同一物体在不同坐标系中的位置和姿态的描述方法,以及量化计算位置和姿态的数学方法。
图片1: 相对于坐标系的矢量p21
2.什么是刚体?
为了简化机器人模型,我们将四足机器狗mini pupper上的各关节零件视作刚体(rigid body),刚体是在运动中和受到力的作用后,形状和大小不变,而且内部各点的相对位置不变的物体。
2.怎样描述刚体的位姿?
位置描述
为了描述mini pupper上的零件在空间中的位置position,在数学中,我们通常用三个正交的带有箭头的单位矢量来描述一个三维坐标系,在这里称为世界坐标系,世界坐标系AAA中的点AP^{A}PAP可以用一个3×13\times13×1的位置矢量来表达,这个矢量可被认为是空间中的一个位置。对于任何一个正交坐标系NNN,都可以有NP^{N}PNP这样一个位置矢量来描述点PPP相对于坐标系NNN的位置关系。
AP=[pxpypz]^AP= \left[ \begin{matrix} p_x\\ p_y\\ p_z \end{matrix} \right] AP=pxpypz
AP^APAP:P点相对于坐标系AAA的位置矢量
pxp_xpx: P向量相对于坐标系AAA的xxx轴方向的分量
姿态描述
mini pupper上的零件刚体除了需要表示位置,通常还需要描述它的姿态attitude,为了描述这个姿态,我们将在物体上固定一个坐标系并且给出这个坐标系相对参考坐标系的描述。
也就是说,我们用一个固定在物体上的坐标系来描述这个物体的姿态,而这个坐标系的描述可以利用相对参考系的三个主轴单位矢量来描述。
用XB^\hat{X_B}XB^ 、YB^\hat{Y_B}YB^ 、ZB^\hat{Z_B}ZB^ 来表示坐标系BBB主轴方向的单位矢量,如果用坐标系AAA来作为参考系,则写作AXB^\hat{^AX_B}AXB^ 、AYB^\hat{^AY_B}AYB^ 、AZB^\hat{^AZ_B}AZB^ ,按前述顺序组成3×13 \times13×1的矩阵,这个矩阵被称为旋转矩阵。
旋转矩阵BAR^A_BRBAR是坐标系BBB相对于参考坐标系AAA的表达:
BAR=(AXB^AYB^AZB^)=[X^B⋅X^AY^B⋅X^AZ^B⋅X^AX^B⋅Y^AY^B⋅Y^AZ^B⋅Y^AX^B⋅Z^AY^B⋅Z^AZ^B⋅Z^A](旋转矩阵)^A_BR =(\hat{^AX_B}\quad\hat{^AY_B}\quad\hat{^AZ_B} ) = \left[ \begin{matrix} \hat X_B\cdot \hat X_A& \hat Y_B\cdot \hat X_A & \hat Z_B\cdot \hat X_A \\ \hat X_B\cdot \hat Y_A& \hat Y_B\cdot \hat Y_A&\hat Z_B\cdot \hat Y_A \\ \hat X_B\cdot \hat Z_A & \hat Y_B\cdot \hat Z_A & \hat Z_B\cdot \hat Z_A \end{matrix} \right] \tag{旋转矩阵} BAR=(AXB^AYB^AZB^)=X^B⋅X^AX^B⋅Y^AX^B⋅Z^AY^B⋅X^AY^B⋅Y^AY^B⋅Z^AZ^B⋅X^AZ^B⋅Y^AZ^B⋅Z^A(旋转矩阵)
BAR^A_BRBAR:坐标系BBB相对于参考坐标系AAA的旋转矩阵
X^B\hat X_BX^B:坐标系BBB的xxx方向的单位矢量
X^A\hat X_AX^A:坐标系AAA的xxx方向的单位矢量
位姿描述
在四足机器狗mini pupper的运动学中,位置和姿态经常成对出现,称之为位姿pose,位姿可以用两个坐标系的相对关系来描述。
结合位置描述与姿态描述,得出一个位姿{B}\left\{ B \right\}{B}可以等价地用一个位置矢量APBORG^AP_{B ORG}APBORG和一个旋转矩阵BAR^A_BRBAR来描述:
{B}={BAR,APBORG}\left\{ B \right\}=\left\{ ^A_BR ,^AP_{B ORG}\right\} {B}={BAR,APBORG}
APBORG^AP_{B ORG}APBORG:确定位姿{B}\left\{ B \right\}{B}的原点的位置矢量,ORG为Origin,即原点之意
4.如何描述刚体的平移与旋转?
坐标平移
在了解完位置、姿态、位姿的概念后,我们将学习如何从一个坐标系变换到另一个坐标系,通常被叫做“映射”,“映射”使得mini pupper的刚体零件可以在不同的参考坐标系中被表达为一个相同的量。
图片2:位姿变换图
下面,就让我们来尝试将一个坐标平移来体会四足机器狗mini pupper上的刚体零件的运动。
坐标平移是简单的运动,在{A}\left\{ A \right\}{A}和{B}\left\{ B \right\}{B}的姿态相同时,{B}\left\{ B \right\}{B}不同与{A}\left\{ A \right\}{A}的只有平移,所以可以用一个位置矢量APBORG^AP_{B ORG}APBORG来描述{B}\left\{ B \right\}{B}的原点相对于{A}\left\{ A \right\}{A}的位置。
图片3:坐标平移图
以下为当姿态相同时,矢量相加的办法求点PPP相对于{A}\left\{ A \right\}{A}的表示AP^APAP:
AP=BP+APBORG^AP= {\kern 2pt}^BP+ {\kern 2pt}^AP_{BORG} AP=BP+APBORG
位置矢量APBORG^AP_{B ORG}APBORG来描述{B}\left\{ B \right\}{B}的原点相对于{A}\left\{ A \right\}{A}的位置。
在映射中,空间中的点本身没有改变,而是描述关系改变了,即点PPP的坐标相对于坐标系B{B}B的关系变换到了相对于坐标系A{A}A的关系。在姿态相同的情况下,矢量APBORG^AP_{B ORG}APBORG包含了变换所需的信息,它定义了这个平移的映射。
坐标旋转
在刚体的姿态描述中我们了解到,姿态可以用坐标系三主轴的单位矢量来描述,那么将这三个单位矢量依次排列,可以得到一个3x33x33x3的旋转矩阵。
通常认为,{B}\left\{ B \right\}{B}相对于{A}\left\{ A \right\}{A}的旋转矩阵表示为BAR^A_BRBAR
因为旋转矩阵各列的模为1,各单位矢量均相互正交,在线性代数中,正交阵的逆矩阵等于它的转置矩阵,可得:
BAR=BAR−1=ABRT^A_BR = ^A_BR^{-1}=^B_AR^T BAR=BAR−1=ABRT
所以一个旋转矩阵可以为三个量为一组的行向量或者是三个量为一组的列向量。
BAR^A_BRBAR矩阵的各列为{B}\{B\}{B}的单位矢量在{A}\{A\}{A}中的描述,即将{B}\{B\}{B}的单位矢量投影到{A}\{A\}{A}的单位矢量方向上。投影是由矢量的点积计算的。
BAR=(AXB^AYB^AZB^)=[X^B⋅X^AY^B⋅X^AZ^B⋅X^AX^B⋅Y^AY^B⋅Y^AZ^B⋅Y^AX^B⋅Z^AY^B⋅Z^AZ^B⋅Z^A](旋转矩阵)^A_BR =(\hat{^AX_B}\quad\hat{^AY_B}\quad\hat{^AZ_B} ) = \left[ \begin{matrix} \hat X_B\cdot \hat X_A& \hat Y_B\cdot \hat X_A & \hat Z_B\cdot \hat X_A \\ \hat X_B\cdot \hat Y_A& \hat Y_B\cdot \hat Y_A&\hat Z_B\cdot \hat Y_A \\ \hat X_B\cdot \hat Z_A & \hat Y_B\cdot \hat Z_A & \hat Z_B\cdot \hat Z_A \end{matrix} \right] \tag{旋转矩阵} BAR=(AXB^AYB^AZB^)=X^B⋅X^AX^B⋅Y^AX^B⋅Z^AY^B⋅X^AY^B⋅Y^AY^B⋅Z^AZ^B⋅X^AZ^B⋅Y^AZ^B⋅Z^A(旋转矩阵)
BAR^A_BRBAR:坐标系BBB相对于参考坐标系AAA的旋转矩阵
X^B\hat X_BX^B:坐标系BBB的xxx方向的单位矢量
X^A\hat X_AX^A:坐标系AAA的xxx方向的单位矢量
因此,对于原点位置相同的两个坐标系{A}\{A\}{A}和{B}\{B\}{B},若要将一点PPP相对坐标系{B}\{B\}{B}的关系转化为对坐标系{A}\{A\}{A}的关系,可得
AP=BARBP^AP= {\kern 2pt}^A_BR {\kern 2pt}^BP AP=BARBP
坐标的一般变换
对于mini pupper上的各零部件之间的变换,通常不只有坐标的平移或变换,而是两者兼有,这就是坐标的一般变换。一般变换采用先旋转,再平移的方法来变换坐标系。
将旋转和平移合并来看,可得
AP=BARBP+APBORG^AP= ^A_BR{\kern 2pt}^BP+ {\kern 2pt}^AP_{BORG} AP=BARBP+APBORG
可以用更简洁的形式:一个4×44 \times 44×4矩阵形式的算子来表示一个坐标系到另一个坐标系的映射。
可以看到式子中用了两个个4×14\times 14×1的位置矢量来分别表示AP^APAP和BP^BPBP,这种位置矢量的末尾分量为1,有没有末尾的这个1取决与这个位置矢量与3x33x33x3还是4x4的矩阵相乘4x4的矩阵相乘4x4的矩阵相乘。
(AP1)=[BARAPBORG0001](BP1)\left( \begin{matrix} ^AP \\ 1 \end{matrix} \right)= \left[ \begin{matrix} ^A_BR &^AP_{BORG}\\ 0{\kern 3pt}0{\kern 3pt}0&1 \end{matrix} \right] \left( \begin{matrix} ^BP \\ 1 \end{matrix} \right) (AP1)=[BAR000APBORG1](BP1)
这个4×44\times 44×4矩阵被称为齐次变换矩阵,它以普通矩阵的形式表示了一般变换中的旋转以及平移。
简写为:
AP=BATBP^AP= {\kern 2pt}^A_BT {\kern 2pt}^BP AP=BATBP
一般来说,常用旋转矩阵定义“姿态”,而齐次变换矩阵常用于定义坐标系,例如坐标系{B}\{B\}{B}相对于{A}\{A\}{A}的变换就可描述为BAT^A_BTBAT
平移算子
算子是坐标系间点映射的通用数学表达式,和前面所描述的方法类似,算子有点平移算子、矢量旋转算子、一般变换算子。
平移算子可以对点进行平移,矢量AQ^AQAQ给出了平移的信息,qqq是沿矢量AQ^AQAQ方向平移的数量。qx、qy、qzq_x、q_y、q_zqx、qy、qz都是平移矢量Q的分量。
例如从AP1^AP_1AP1点平移到AP2^AP_2AP2点
AP2=DQ(q)AP1^AP_2 = D_Q(q)^AP_1 AP2=DQ(q)AP1
DQ(q)=[100qx010qy001qz0001]D_Q(q) = \left[ \begin{matrix} 1 & 0 & 0&q_x \\ 0 & 1 & 0 &q_y\\ 0 & 0 & 1&q_z \\ 0 & 0 & 0&1 \\ \end{matrix} \right] DQ(q)=100001000010qxqyqz1
旋转算子
对于平面内图形或坐标系的旋转,可以视作这个图形或坐标系上各点相对于原坐标系的旋转得来。
如图所示,坐标为(x,y)(x,y)(x,y)的点PPP旋转角度θ\thetaθ到点P′P'P′,旋转后坐标为(x′,y′)(x',y')(x′,y′)。
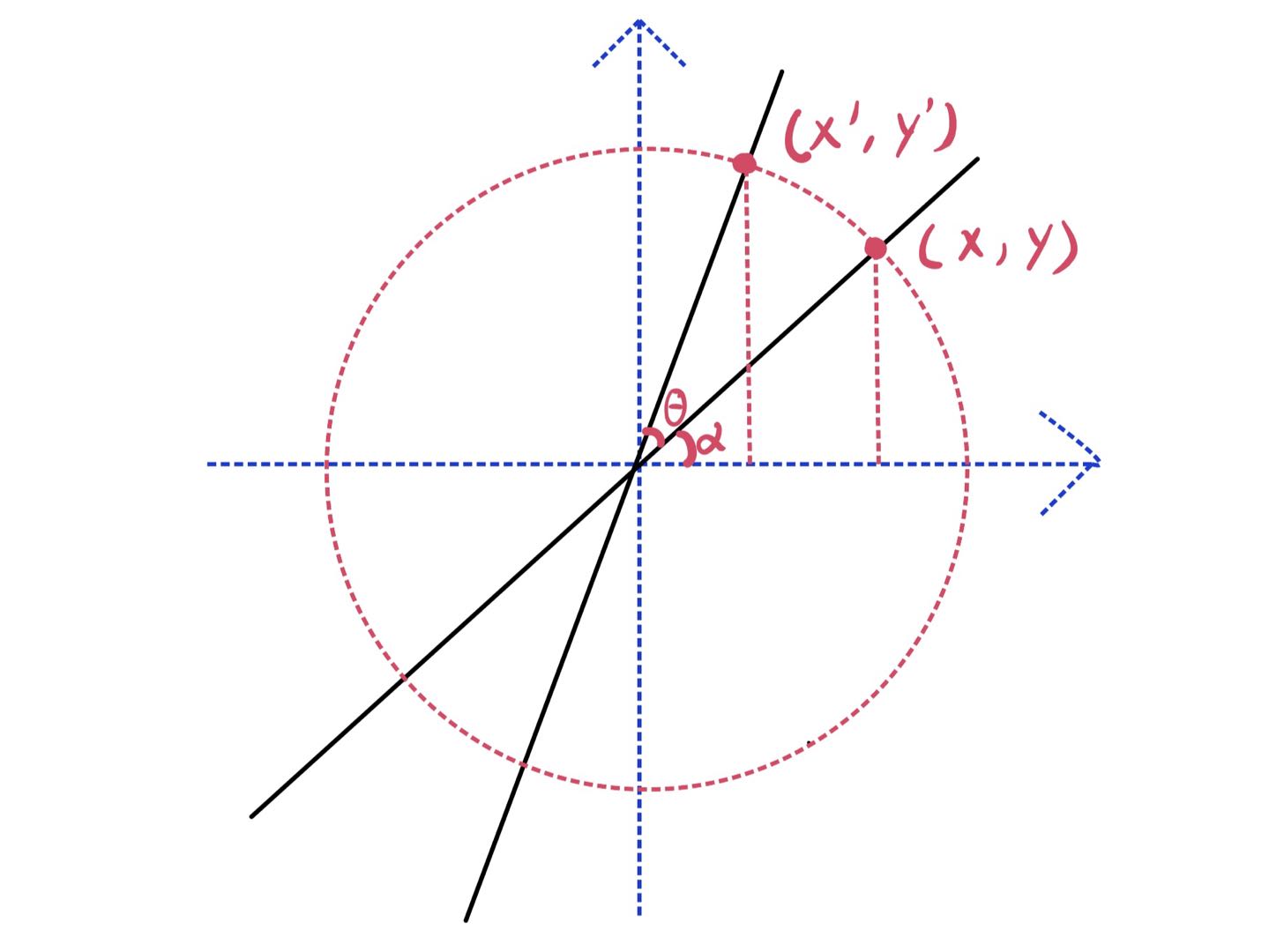
r=(x2+y2)r=\sqrt{(x^2 + y^2)} r=(x2+y2)
x=r⋅Cosαy=r⋅Sinαx=r·Cos\alpha \quad y=r·Sin\alpha x=r⋅Cosαy=r⋅Sinα
x′=r⋅Cos(α+θ)y′=r⋅Sin(α+θ)x'=r·Cos(\alpha+\theta) \quad y'=r·Sin(\alpha+\theta) x′=r⋅Cos(α+θ)y′=r⋅Sin(α+θ)
可得平面点绕原点旋转公式:
x′=xCosθ−ySinθy′=xSinθ+yCosθx'=xCos\theta-ySin\theta \quad y'=xSin\theta+yCos\theta x′=xCosθ−ySinθy′=xSinθ+yCosθ
绕z轴旋转θ\thetaθ的旋转算子RRR将矢量AP1^AP_1AP1旋转变换为AP2^AP_2AP2
AP2=RAP1^AP_2 = R^AP_1 AP2=RAP1
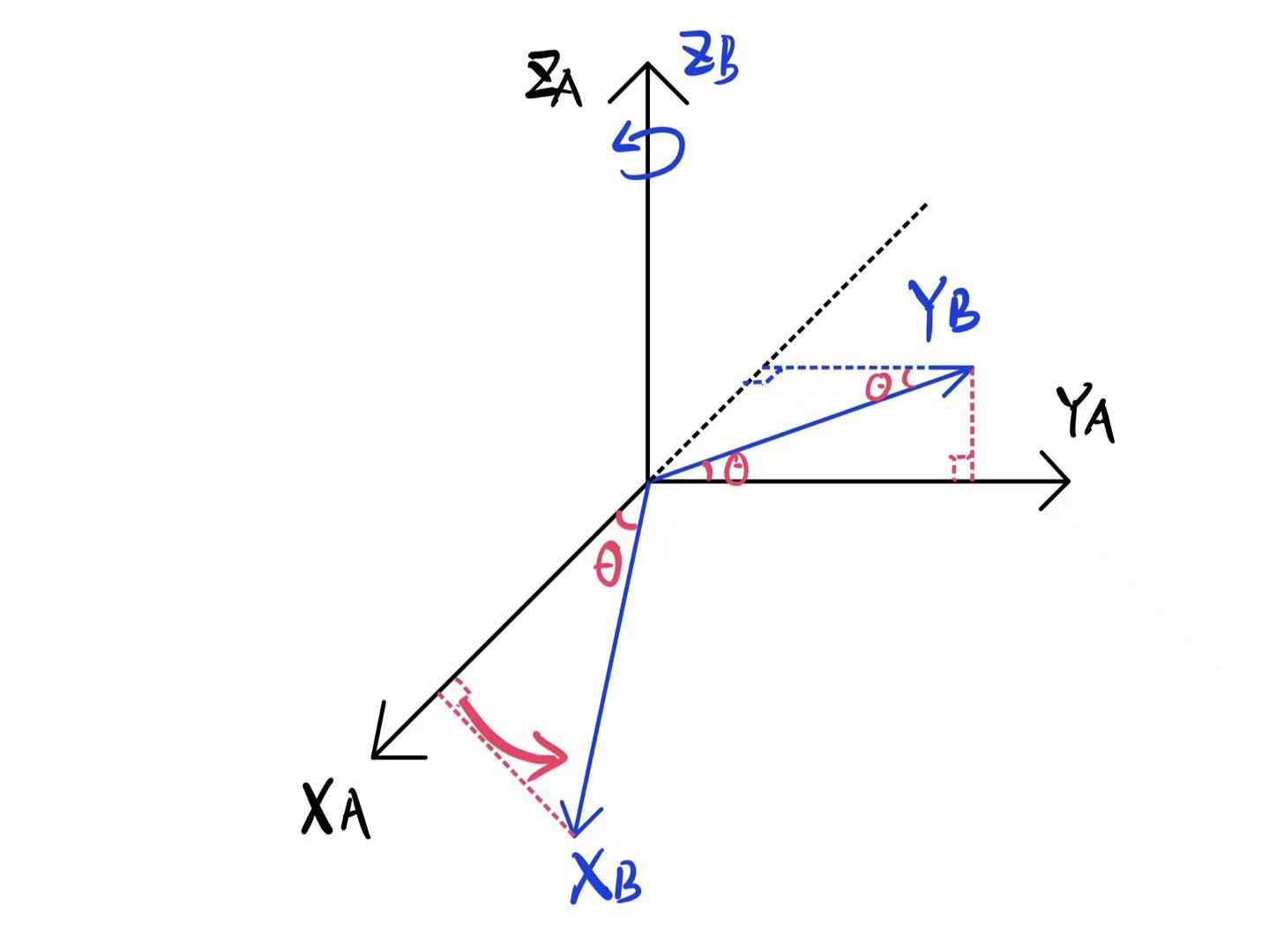
该旋转算子的各列可看做旋转后的各单位矢量在旋转前单位矢量上的投影,可以发现和平面点绕原点旋转公式是逻辑一致的。
Rz(θ)=[Cosθ−Sinθ00SinθCosθ0000100001]R_z(\theta) = \left[ \begin{matrix} Cos\theta & -Sin\theta & 0&0 \\ Sin\theta & Cos\theta & 0 &0\\ 0 & 0 & 1&0 \\ 0 & 0 & 0&1 \\ \end{matrix} \right] Rz(θ)=CosθSinθ00−SinθCosθ0000100001
一般变换算子
同理,结合旋转与平移,可得一般变换算子
AP2=TAP1^AP_2 = T^AP_1 AP2=TAP1
算子、映射、位姿描述都是齐次变换矩阵的解释,具体倾向哪个解释则取决于你对该矩阵的用途是倾向于描述还是变换。
5. matplotlib
matplotlib是Python语言及其数值计算库NumPy的绘图库。它的设计与MATLAB非常类似,能够在Python中方便地绘制图像。
参考链接:matplotlib
6. numpy
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库,因此可以用来计算坐标系的变换。
参考链接:numpy
7. 绘制向量的函数
ax.quiver(起点x, 起点y, 起点z,x方向数值, y方向数值, z方向数值,arrow_length_ratio=箭头箭身比, color="颜色")
8. 用户的输入部分
move_pre= input("请输入坐标系原点相对参考坐标系原点平移的x、y、z分量:")
move = [int(n) for n in move_pre.split()]
print(move)
rotate_pre= input("请输入坐标系绕参考坐标系x轴、y轴、z轴依次旋转的角度:") # 旋转采用Fixed Angles模式
rotate = [int(n) for n in rotate_pre.split()]
print(rotate)
9. 安装matplotlib和numpy环境
sudo apt install pip # 安装pip
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple # 换源
sudo pip install matplotlib # 安装matplotlib
sudo pip install numpy # 安装numpy
实验步骤
1. 编写Python程序 vector_rotation.py
#!/usr/bin/python
# coding:utf-8
# vector_rotation.py
# 使参考坐标系内的一指定向量绕x、y、z轴旋转指定角度,并依次按红、橙、绿、蓝绘制出原向量和旋转后的向量
import matplotlib.pyplot as plt # 引入matplotlib库
import numpy as np # 引入numpy库def rotate_X(x, y, z, alpha):alpha = alpha * (np.pi / 180)x_r = xy_r = np.cos(alpha)*y - np.sin(alpha)*zz_r = np.sin(alpha)*y + np.cos(alpha)*zprint(f"Test_X-axis:{(x, y, z)} rotate {alpha*(180/np.pi)} degrees,result: {(x_r, y_r, z_r)}")return x_r, y_r, z_rdef rotate_Y(x, y, z, beta):beta = beta * (np.pi / 180)x_r = np.cos(beta)*x + np.sin(beta)*zy_r = yz_r = -np.sin(beta)*x + np.cos(beta)*zprint(f"Test_Y-axis:{(x, y, z)} rotate {alpha*(180/np.pi)} degrees,result: {(x_r, y_r, z_r)}")return x_r, y_r, z_rdef rotate_Z(x, y, z, gamma):gamma = gamma * (np.pi / 180)x_r = np.cos(gamma)*x - np.sin(gamma)*yy_r = np.sin(gamma)*x + np.cos(gamma)*yz_r = zprint(f"Test_Z-axis:{(x, y, z)} rotate {alpha*(180/np.pi)} degrees,result: {(x_r, y_r, z_r)}")return x_r, y_r, z_rdef draw_before(px,py,pz):x_vector = ax.quiver(origin[0], origin[1], origin[2],ac2 * x_axis_unit_vector[0], ac2 * x_axis_unit_vector[1], ac2 * x_axis_unit_vector[2],arrow_length_ratio=0.1, color="black") # 绘制A坐标系的x单位向量y_vector = ax.quiver(origin[0], origin[1], origin[2],ac2 * y_axis_unit_vector[0], ac2 * y_axis_unit_vector[1], ac2 * y_axis_unit_vector[2],arrow_length_ratio=0.1, color="black") # 绘制A坐标系的y单位向量z_vector = ax.quiver(origin[0], origin[1], origin[2],ac2 * z_axis_unit_vector[0], ac2 * z_axis_unit_vector[1], ac2 * z_axis_unit_vector[2],arrow_length_ratio=0.1, color="black") # 绘制A坐标系的z单位向量p_vector = ax.quiver(origin[0], origin[1], origin[2],px, py, pz,arrow_length_ratio=0.1, color="red") # 绘制A坐标系的p向量print(px, py, pz)# plot_init
fig = plt.figure() # 建立图像
ax = fig.add_subplot(projection="3d") # 为图像添加三维坐标系
#ax.grid(False) # 取消网格线,如需要网格线,请注释该行
# Setting the axes properties
ax.set(xlim3d=(0, 5), xlabel='X')
ax.set(ylim3d=(0, 5), ylabel='Y')
ax.set(zlim3d=(0, 5), zlabel='Z')# variable_init
origin = [0, 0, 0]
x_axis_unit_vector = [1, 0, 0]
y_axis_unit_vector = [0, 1, 0]
z_axis_unit_vector = [0, 0, 1]
# ac = 6 # 坐标轴底色向量增益系数
ac2 = 4 # A坐标系增益系数# # 绘制坐标轴底色向量
# ax.quiver(origin[0], origin[1], origin[2],
# ac*x_axis_unit_vector[0], ac*x_axis_unit_vector[1], ac*x_axis_unit_vector[2],
# arrow_length_ratio=0.1, color="black") # 绘制x方向底色向量
# ax.quiver(origin[0], origin[1], origin[2],
# ac*y_axis_unit_vector[0], ac*y_axis_unit_vector[1], ac*y_axis_unit_vector[2],
# arrow_length_ratio=0.1, color="black") # 绘制y方向底色向量
# ax.quiver(origin[0], origin[1], origin[2],
# ac*z_axis_unit_vector[0], ac*z_axis_unit_vector[1], ac*z_axis_unit_vector[2],
# arrow_length_ratio=0.1, color="black") # 绘制z方向底色向量vector_in_A_pre= input("请分别输入该向量在参考坐标系A中的xyz分量,以空格隔开:")
vector_in_A = [int(n) for n in vector_in_A_pre.split()]
print("向量相对参考坐标系:", vector_in_A)
rotate_pre= input("请输入向量绕参考坐标系x轴、y轴、z轴依次旋转的角度(角度制):") # 旋转采用Fixed Angles模式
rotate = [int(n) for n in rotate_pre.split()]
print("向量分别绕x,y,z轴:", rotate)
alpha = rotate[0]
beta = rotate[1]
gamma = rotate[2]draw_before(vector_in_A[0], vector_in_A[1], vector_in_A[2]) # 绘制原坐标系及原指定向量first_vector = rotate_X(vector_in_A[0], vector_in_A[1], vector_in_A[2],alpha)
p1_vector = ax.quiver(origin[0], origin[1], origin[2],first_vector[0], first_vector[1], first_vector[2],arrow_length_ratio=0.1, color="orange") # 绘制绕x旋转后的p向量
second_vector = rotate_Y(first_vector[0], first_vector[1], first_vector[2],beta)
p2_vector = ax.quiver(origin[0], origin[1], origin[2],second_vector[0], second_vector[1], second_vector[2],arrow_length_ratio=0.1, color="green") # 绘制绕y旋转后的p向量
third_vector = rotate_Z(second_vector[0], second_vector[1], second_vector[2],gamma)
p3_vector = ax.quiver(origin[0], origin[1], origin[2],third_vector[0], third_vector[1], third_vector[2],arrow_length_ratio=0.1, color="blue") # 绘制绕z旋转后的p向量plt.show() # 绘制
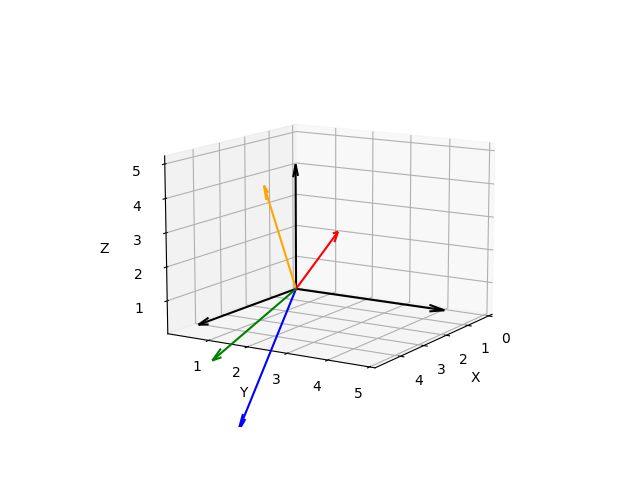
2. 运行程序,观察效果
在vector_rotation.py的目录下执行以下命令:
sudo python vector_rotation.py
输入对应的转动角度,此时应观察到向量绕各轴依次转动后的变化。
实验总结
经过本知识点的学习和实验操作,你应该能达到以下水平:
| 知识点 | 内容 | 了解 | 熟悉 | 掌握 |
|---|---|---|---|---|
| 刚体 | 刚体的平动、转动基础知识 | ✔ | ||
| 位姿 | 位姿的描述 | ✔ | ||
| 坐标变换 | 坐标系之间的变换 | ✔ |
版权信息:教材尚未完善,此处预留版权信息处理方式
mini pupper相关内容可访问:https://github.com/mangdangroboticsclub
相关文章:

实例8:机器人的空间描述和变换仿真
实例8:机器人的空间描述和变换仿真 实验目的 通过刚体与刚体的平动、转动基础知识的学习,熟悉位姿的描述通过Python编程实践,可视化学习坐标系的变换,熟悉空间变换 实验要求 通过python编程,输入一指定向量和对应的…...

网络 导航
目录内容链接网络网络参考文章:【网络】http请求 调试网络问题解决参考文章:【问题解决】网络 IP DNS解析网络问题解决参考文章:【问题解决】网络 TCP 规则 抓包网络问题解决参考文章:【问题解决】网络 Http请求 调试网络问题解决…...
Web Spider Ast-Hook 浏览器内存漫游-数据检索
文章目录一、资源下载二、通过npm安装anyproxy模块三、anyproxy的介绍以及基本使用1. anyproxy的功能介绍2. anyproxy的基本使用四、给浏览器挂代理五、实操极验demo案例总结提示:以下是本篇文章正文内容,下面案例可供参考 一、资源下载 Github&#x…...

计算机网络笔记、面试八股(二)——HTTP协议
本章目录2. HTTP协议2.1 HTTP协议简介2.2 HTTP协议的优点2.3 HTTP协议的缺点2.4 HTTP协议属于哪一层2.5 HTTP通信过程2.6 常见请求方法2.7 GET和POST的区别2.8 请求报文与响应报文2.8.1 HTTP请求报文2.8.2 HTTP响应报文2.9 响应状态码2.10 HTTP 1.0和1.1的区别2.10.1 长连接2.1…...
docker快速上手使用
文章目录一、docker概述1. 为什么需要docker2. 什么是docker3. docker和虚拟机的区别4. docker三要素二、docker安装1. 添加app源2. 安装docker社区版3. 更换国内docker镜像源三、docker基本使用方法1. 获取镜像2. 查看当前系统中的docker镜像3. 运行docker容器4. 查看当前存在…...
<c++> 类的构造函数与类的析构函数
文章目录类的构造函数什么是构造函数声明和定义构造函数如何使用构造函数默认构造函数类的析构函数什么是析构函数声明和定义析构函数小练习银行账户执行效果类的构造函数 什么是构造函数 Q:什么是类的构造函数 A:构造函数是类的一种特殊成员函数,不需…...
)
华为OD机试真题Java实现【玩牌高手】真题+解题思路+代码(20222023)
玩牌高手 给定一个长度为n的整型数组,表示一个选手在n轮内可选择的牌面分数。选手基于规则选牌, 请计算所有轮结束后其可以获得的最高总分数。 选择规则如下: 1、在每轮里选手可以选择获取该轮牌面,则其总分数加上该轮牌面分数,为其新的总分数。 2、选手也可不选择本轮…...

Hive Sql整体优化思路
如果遇到sql性能问题,可以先查看4040页面的sql执行信息。一个sql解析为多个stage,一个stage分为多个task。对问题Sql的某一个stage,基本的分析思路如下:所有的task都慢,检查下是否有笛卡尔积(关联字段重复值、关联字段…...

【华为OD机试模拟题】用 C++ 实现 - 数组的中心位置(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
)
取指定数值的地址 (int 转 void *)
int a 0x12345678 是一个地址void *p (void *)a; 提示下马错误;Error: cast to pointer from integer of different size [-Werrorint-to-pointer-cast]This error occurs when there is an attempt to convert an integer to a pointer of a different size. Thi…...
C#的多线程、线程池和Task
线程 被定义为程序的执行路径。每个线程都定义了一个独特的控制流。如果您的应用程序涉及到复杂的和耗时的操作,那么设置不同的线程执行路径往往是有益的,每个线程执行特定的工作。 线程是轻量级进程。一个使用线程的常见实例是现代操作系统中并行编程的…...
Day20【元宇宙的实践构想06】—— 元宇宙与Web3.0
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:元宇宙 部分资料参考文献: 成生辉教授的《元宇宙:概念、技术及生态》和百度相关…...

极限熵和冗余度
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 信息冗余度(多余度、剩余…...

女生学习大数据专业未来前景怎么样
学习大数据与性别没有什么太大关系,各有优势。就目前的发展前景来说,大数据还是非常不错的,至于好不好就业就要看你个人学习的怎么样,以及学历是否过关了~ 据《新职业——大数据工程技术人员就业景气现状分析报告》显示ÿ…...
主题模型实践
目录 一.TF-IDF 二.LSI 三.相似度 四.主题和主题分布 五. LDA计算的相似度 六.LDA过程 七.主题 八.主题和主题分布 九.数据处理流程 十.常用正则表达式 十一.代码 一.TF-IDF 二.LSI 三.相似度 四.主题和主题分布 五. LDA计算的相似度 六.LDA过程 七.主题 八.主题和主…...

按字典序排列的最小的等价字符串[拆解并查集]
并查集前言一、按字典序排列的最小的等价字符串二、并查集总结参考文献前言 并查集有什么用?并查集是什么?搞懂这两个问题,相关的并查集问题就变得非常easy! 一、按字典序排列的最小的等价字符串 二、并查集 有一种方法&#x…...

操作系统——6.系统调用
目录 1.概述 2.系统调用的定义和作用 2.1 定义 2.2 功能 2.3 分类 3.系统调用和库函数的区别 4.系统调用背后的过程 5.小结 1.概述 这篇文章我们主要来介绍一下操作系统中的系统调用,下面来看一下具体的框架图: 2.系统调用的定义和作用 2.1 定…...

JavaScript DOM操作
目录 获取元素: 修改元素属性: 添加、删除、替换元素: 修改样式: DOM(文档对象模型)是一种用于操作 HTML 和 XML 文档的 API。JavaScript 通过 DOM API 可以访问和操作页面中的元素、属性和样式等。 获…...

【数据结构】顺序表
文章目录前言初始化顺序表打印顺序表检查容量判空顺序表数据个数尾部插入尾部删除头部插入头部删除在pos位置插入数据删除pos位置的数据查找数据修改数据销毁顺序表整体代码写在最后前言 顺序表作为数据结构中的小小弟,还是很好应付的。说到数据结构,顺序…...

【人工智能 AI 】RPA 架构师需要具备的技能有哪些?RPA Solution Architect
RPA 架构师需要具备的技能有哪些?使用markdown格式,不少于3000字,细化到3级目录。 文章目录 一、RPA架构师需要具备的技能1. 对RPA的理解2. 对RPA技术的熟练掌握2.1 RPA系统的架构模式2.2 RPA软件的操作模式2.3 RPA程序的编写方式3. 对RPA应用的知识4. 对软件开发的基本知识…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
