Atcoder abc257 E
E - Addition and Multiplication 2
题意:
给你一个数字n表示你现在拥有的金额
然后给你1~9每个经营额所需要的成本, 设总经营额为x, 当前使用的经营额为y, 则每一次使用经营额时都有x=10*x+y
问, 如何在使用不大于成本数量的金额下, 使得经营额最高
例如:
5 5 4 3 8 1 6 7 6 4成本为5
接下来为1~9的经营额
1 2 3 4 5 6 7 8 9
5 4 7 8 2 6 7 6 3
先选择9的经营额: 现在有x=0+9 此时n=5-3=2
再选择5的经营额: 现在有x=9*10+5 此时n=2-2=0
首先根据贪心的思想
我们很容易想得到, 想要尽可能得到一个大的数字, 先考虑位数更大, 再考虑高位数字更大
那么对于此题
我们先算出成本在1~9的经营额下最小的成本能使用的最多次数(也就是考虑多的位数)
次数=总成本/经营额下的最小成本
算出次数之后考虑数字能否在保持位数最大的同时在高位数字贪心
void solve()
{cin>>n;ll mmin=0x3f3f3f3f;for(int i=1;i<=9;i++){cin>>arr[i];mmin=min(mmin,arr[i]);//找出成本最小的数字}m=n/mmin;//最大位数for(int i=0;i<=m;i++)/对每一位数枚举 从高位开始枚举for(int j=9:j>=1;j--)//贪心{if(n-arr[j]>=mmin*(m-i))//保持位数最大的同时在高位数字贪心{n-=arr[j];cout<<j;break;}}return;
}相关文章:

Atcoder abc257 E
E - Addition and Multiplication 2 题意: 给你一个数字n表示你现在拥有的金额 然后给你1~9每个经营额所需要的成本, 设总经营额为x, 当前使用的经营额为y, 则每一次使用经营额时都有x10*xy 问, 如何在使用不大于成本数量的金额下, 使得经营额最高 例如: 5 5 4 3 8 1 6 7 …...

模拟退火算法改进
import numpy as np import matplotlib.pyplot as plt import math import random from scipy.stats import norm from mpl_toolkits.mplot3d import Axes3D # 目标函数 def Function(x, y): return -20 * np.exp(-0.2*np.sqrt(0.5*(x*xy*y)))\ -np.exp(0.5*(n…...
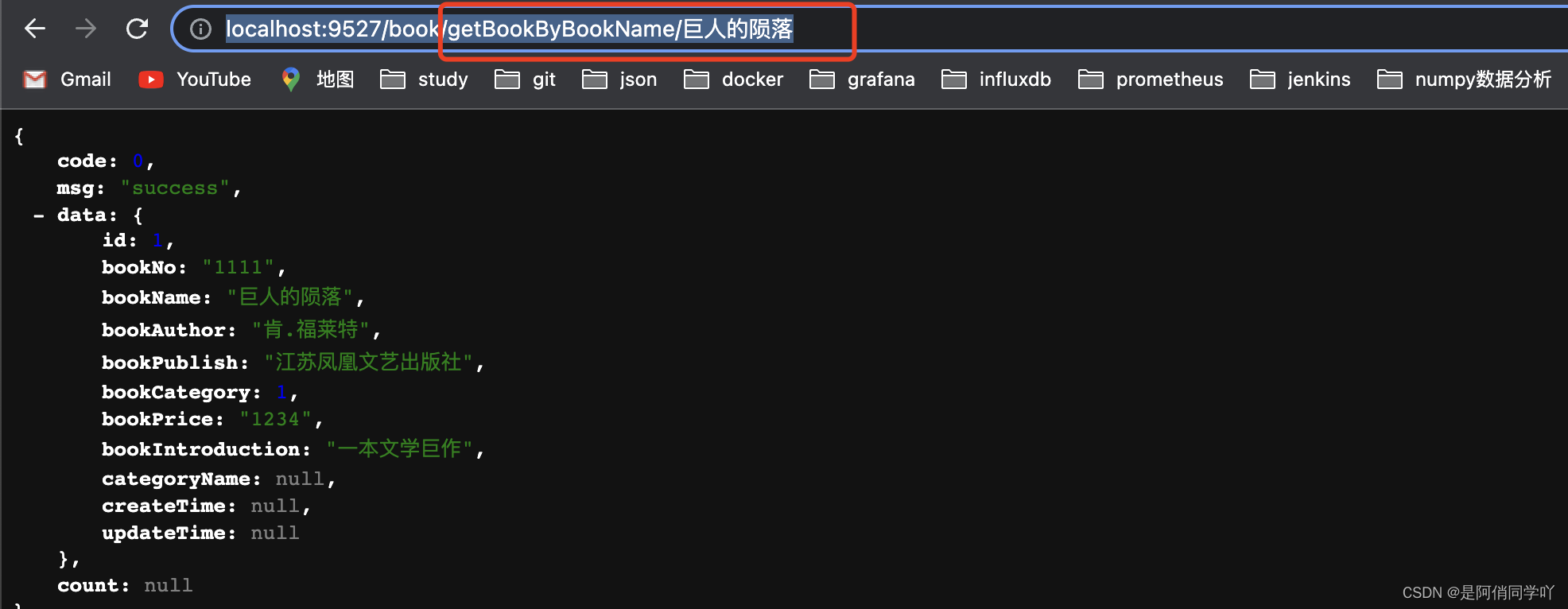
SpringBoot+HttpClient+JsonPath提取A接口返回值作为参数调用B接口
前言 在做java接口自动化中,我们常常需要依赖多个接口,A接口依赖B,C,D接口的响应作为请求参数;或者URL中的参数是从其他接口中提取返回值作获取参数这是必不可少的。那么怎么实现呢?下面就来介绍多业务依赖…...

JUC 之 CompletableFuture
——CompletableFuture Future Future 接口(FutureTask 实现类) 定义了操作异步任务执行的一些方法,如获取异步的执行结果、取消任务的执行、判断任务是否被取消、判断任务执行是否完毕例如: 主线程让一个子线程去执行任务&…...

7-vue-1
谈谈你对MVVM的理解 为什么要有这些模式,目的:职责划分、分层(将Model层、View层进行分类)借鉴后端思想,对于前端而已,就是如何将数据同步到页面上 MVC模式 代表:Backbone underscore jquer…...
OpenAPI SDK组件介绍
背景 公司成立以来,积累了数以万计的可复用接口。上层的SaaS业务,原则上要复用这些接口开发自己的业务,为了屏蔽调用接口的复杂性,基础服务开发了apisdk组件,定义了一套声明OpenAPI的注解、注解解析器,实例…...

【Java】Synchronized锁原理和优化
一、synchronized介绍 synchronized中文意思是同步,也称之为”同步锁“。 synchronized的作用是保证在同一时刻, 被修饰的代码块或方法只会有一个线程执行,以达到保证并发安全的效果。 synchronized是Java中解决并发问题的一种最常用的方法…...
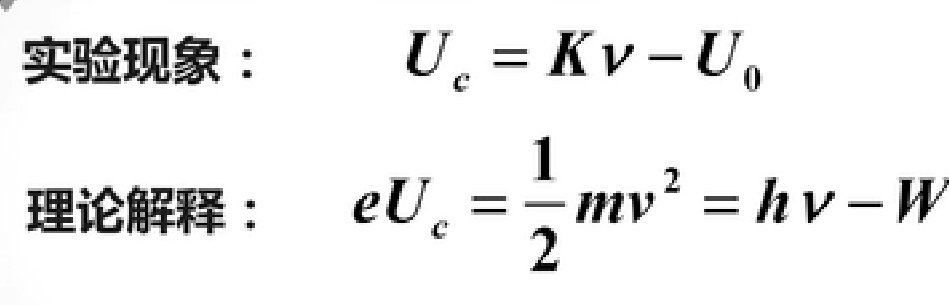
西北工业大学2020-2021学年大物(I)下期末试题选填解析
2 位移电流。磁效应服从安培环路,热效应不服从焦耳-楞次定律。注意,它是变化的电场而非磁场产生。3 又考恒定磁场中安培环路定理。4感生电场5 麦克斯韦速率分布函数。6 相同的高温热源和低温热源之间的一切可逆热机的工作效率相等,无论工质如…...

PHP - ChatGpt API 接入 ,代码,亲测!(最简单!)
由于最近ChatGpt 大火,但是门槛来说是对于大家最头疼的环节, 我自己也先开发了一个个人小程序!大家可以访问使用下, 由此ChatGpt 有一个API 可以仅供大伙对接 让我来说下资质: 1:首先要搞得到一个 ChatGp…...
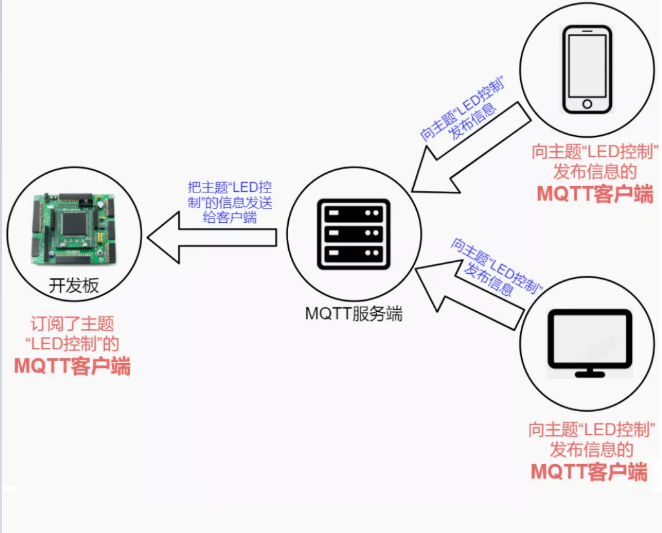
物联网MQTT协议简单介绍
物联网曾被认为是继计算机、互联网之后,信息技术行业的第三次浪潮。随着基础通讯设施的不断完善,尤其是 5G 的出现,进一步降低了万物互联的门槛和成本。物联网本身也是 AI 和区块链应用很好的落地场景之一,各大云服务商也在纷纷上…...
Dubbo 源码解读:负载均衡策略
概览 org.apache.dubbo包下META-INF/dubbo/internal/org.apache.dubbo.rpc.cluster.LoadBalance中内部spi实现类有以下几种: randomorg.apache.dubbo.rpc.cluster.loadbalance.RandomLoadBalance roundrobinorg.apache.dubbo.rpc.cluster.loadbalance.RoundRobinL…...
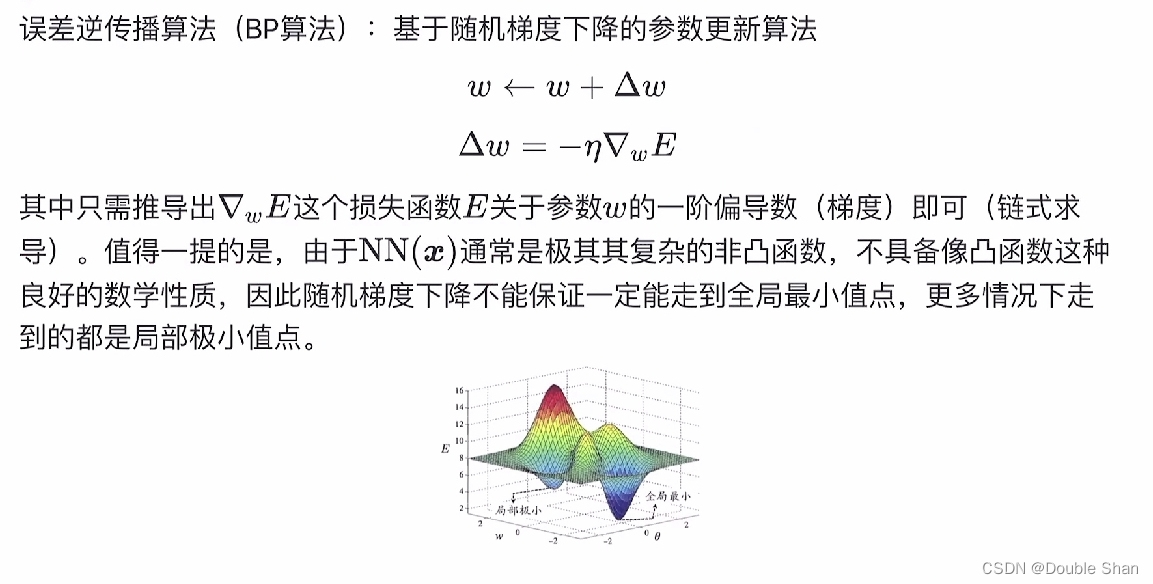
吃瓜教程笔记—Task04
神经网络 知识点 M-P神经元 模型如图所示: 神经元的工作机理:神经元接收来到n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过…...
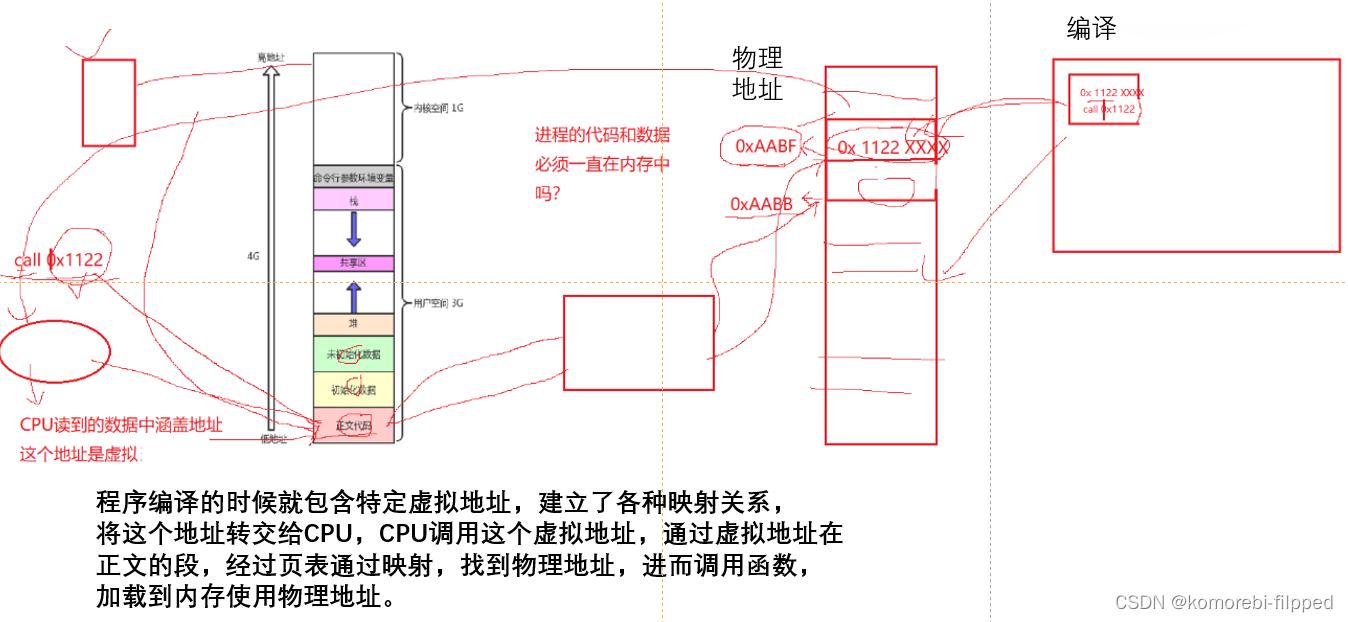
进程地址空间(虚拟地址空间)
目录 引入问题 测试代码 引入地址空间 故事1: 故事二: 解决问题 为什么有虚拟地址空间 扩展 扩展1(没有地址空间,OS如何工作) 扩展2 (代码只读深入了解) 扩展3(malloc本质…...

【项目精选】基于Vue + ECharts的数据可视化系统的设计与实现(论文+源码+视频)
今天给小伙伴们推荐一款超优秀的全新Vue3.0大数据系统Vue3-bigData。 点击下载源码 vue3-bigdata 基于vue3.0echarts构建的可视化大屏图表展示系统。包括各种可视化图表及Vue3新API使用。 功能 柱状图、饼图、词云图、漏斗图 水球图、折线图 仪表盘、雷达图 矩形树图、关系…...

JavaScript Window Screen
文章目录JavaScript Window ScreenWindow ScreenWindow Screen 可用宽度Window Screen 可用高度JavaScript Window Screen window.screen 对象包含有关用户屏幕的信息。 Window Screen window.screen对象在编写时可以不使用 window 这个前缀。 一些属性: screen…...

【双重注意机制:肺癌:超分】
Dual attention mechanism network for lung cancer images super-resolution (肺癌图像超分辨率的双重注意机制网络) 目前,肺癌的发病率和死亡率均居世界恶性肿瘤之首。提高肺部薄层CT的分辨率对于肺癌筛查的早期诊断尤为重要。针对超分辨…...

各种中间件的使用
init background 这一部分我们学习一些常用的, 但是不需要深入理解的中间件 , 例如kafka ,分布式文件系统。 summary Content what is kafka? What time to used it ? 其实消息队列就是解决系统之间复杂交互例如聊天系统和交易系统, …...

Systemverilog覆盖率的合并和计算方式
在systemverilog中,对于一个covergroup来说,可能会有多个instance,我们可能需要对这些instance覆盖率进行操作。 只保存covergroup type的覆盖率,不需要保存instance-specified的覆盖率coverage type和instance-specified的覆盖率…...

(周末公众号解读系列)2000字-视觉SLAM综述
参考链接:https://mp.weixin.qq.com/s?__bizMzg2NzUxNTU1OA&mid2247528395&idx1&sn6c9290dd7fd926f11cbaca312fbe99a2&chksmceb84202f9cfcb1410353c805b122e8df2e2b79bd4031ddc5d8678f8b11c356a25f55f488907&scene126&sessionid1677323905…...

力扣29-两数相除
29. 两数相除 给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。 整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 &#x…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
