代码随想录算法训练营 || 贪心算法 455 376 53
Day27
贪心算法基础
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
刷题或者面试的时候,手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
贪心没有套路,说白了就是常识性推导加上举反例。
455.分发饼干
力扣题目链接
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
思路
贪心算法,每一次都拿着一个小孩,让这个小孩去吃尺寸最小的饼干,这样能达到全局最优,尽量能喂饱更多的小孩
先把数组进行排序,因为要有序
用index来处理小孩,i来遍历饼干,因为对每个小孩,饼干的尺寸要不断移动
都从最小开始,如果遍历到某个位置饼干能满足小孩,那count++,同时这个小孩被满足了,index++
最后返回count
或者是每一次拿着一个饼干,让这个饼干尽可能满足胃口大的小孩,所以要遍历小孩,找到符合要求的,饼干位置减一
代码
class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);//先排序int count = 0;//满足的胃口int index = 0;//小孩的位置for (int i = 0; i < s.length && index < g.length; i++){//饼干进行遍历,因为要看哪个饼干能满足小孩if (s[i] >= g[index]){//找到了符合要求的count++;index++;//小孩位置自增}}return count;}
}class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int index = s.length - 1;for (int i = g.length - 1; i >= 0; i--){if (index >= 0 && s[index] >= g[i]){count++;index--;}}return count;}
}376. 摆动序列
力扣题目链接
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
思路
这个解法很巧妙
先剪枝,如果长度小于2,直接return 1
之后使用up和down进行记录
从1开始遍历,因为要和前一个元素进行比较
如果比前一个大,那up就是down + 1
如果比前一个小,那down就是up + 1
最后返回两者较大值即可
代码
class Solution {public int wiggleMaxLength(int[] nums) {if (nums.length < 2) return 1;int up = 1;int down = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] < nums[i - 1]) down = up + 1;if (nums[i] > nums[i - 1]) up = down + 1;}return Math.max(up,down);}
}53. 最大子序和
力扣题目链接
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
思路
先简单看一下暴力解法
外层循环给出子数组起始位置,内层循环不断遍历后面的元素并更新res
时间复杂度O(n2)
贪心算法
贪心的点在于,计算一个连续和,如果遍历到某个元素,加上这个元素让连续和变为负数了,那我们就把连续和置为0,从下一个元素开始重新计算连续和,因为加上一个负数肯定会让结果变小
代码
class Solution {public int maxSubArray(int[] nums) {int res = Integer.MIN_VALUE;int sum;for (int i = 0; i < nums.length; i++){sum = 0;for (int j = i; j < nums.length; j++){sum += nums[j];res = Math.max(res,sum);}}return res;}
}class Solution {public int maxSubArray(int[] nums) {int res = Integer.MIN_VALUE;int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];//加上这个位置的元素res = Math.max(res,sum);//这句话要写在前面,否则全是负数的情况会返回0,不断更新resif (sum < 0){//如果连续和变为负数了sum = 0;//把连续和置为0,继续遍历}}return res;//最后返回res}
}相关文章:

代码随想录算法训练营 || 贪心算法 455 376 53
Day27贪心算法基础贪心的本质是选择每一阶段的局部最优,从而达到全局最优。刷题或者面试的时候,手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。做题的时候,只要想清楚 局部最优 是什么&…...

PMP考前冲刺2.25 | 2023新征程,一举拿证
题目1-2:1.项目经理正在进行挣值分析,计算出了当前的成本偏差和进度偏差。发起人想要知道基于当前的绩效水平,完成所有工作所需的成本。项目经理应该提供以下哪一项数据?A.完工预算(BAC)B.完工估算(EAC)C.完工尚需估算(ETC)D.完工偏差(VAC)2…...

【自然语言处理】Topic Coherence You Need to Know(主题连贯度详解)
Topic Coherence You Need to Know皮皮,京哥皮皮,京哥皮皮,京哥CommunicationUniversityofChinaCommunication\ University\ of\ ChinaCommunication University of China 在大多数关于主题建模的文章中,常用主题连贯度ÿ…...

C++入门:模板
模板是泛型编程的基础,泛型编程即以一种独立于任何特定类型的方式编写代码。模板是创建泛型类或函数的蓝图或公式。库容器,比如迭代器和算法,都是泛型编程的例子,它们都使用了模板的概念。每个容器都有一个单一的定义,…...
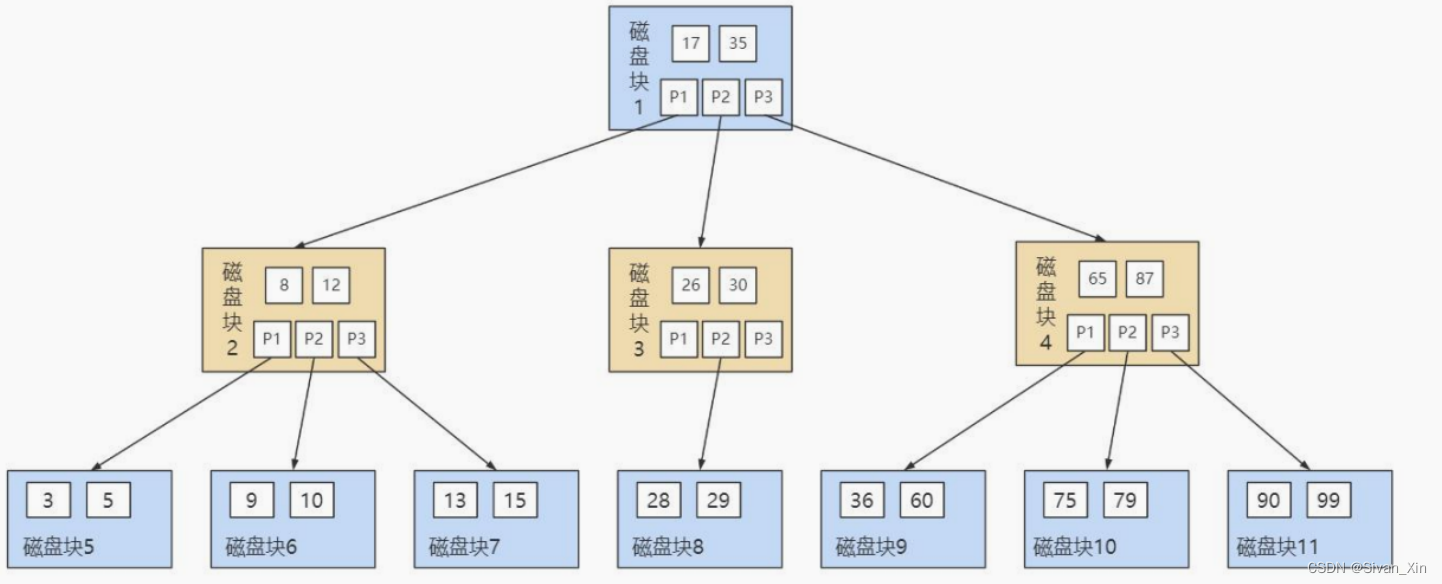
【MySQL】索引常见面试题
文章目录索引常见面试题什么是索引索引的分类什么时候需要 / 不需要创建索引?有什么优化索引的方法?从数据页的角度看B 树InnoDB是如何存储数据的?B 树是如何进行查询的?为什么MySQL采用B 树作为索引?怎样的索引的数…...

【Web逆向】万方数据平台正文的逆向分析(上篇--加密发送请求)—— 逆向protobuf
【Web逆向】万方数据平台正文的逆向分析(上篇--加密发送请求)—— 逆向protobuf声明一、了解protobuf协议:二、前期准备:二、目标网站:三、开始分析:我们一句句分析:先for循环部分:后…...

Amazon S3 服务15岁生日快乐!
2021年3月14日,作为第一个发布的服务,Amazon S3 服务15周岁啦!在中国文化里,15岁是个临界点,是从“舞勺之年”到“舞象之年”的过渡。相信对于 Amazon S3 和其他的云服务15周岁也将是其迎接更加美好未来的全新起点。亚…...

【python】函数详解
注:最后有面试挑战,看看自己掌握了吗 文章目录基本函数-function模块的引用模块搜索路径不定长参数参数传递传递元组传递字典缺陷,容易改了原始数据,可以用copy()方法避免变量作用域全局变量闭包closurenonlocal 用了这个声明闭包…...

AoP-@Aspect注解处理源码解析
对主类使用EnableAspectJAutoProxy注解后会导入组件, Import(AspectJAutoProxyRegistrar.class) public interface EnableAspectJAutoProxy {AspectJAutoProxyRegistrar类实现了ImportBeanDefinitionRegistrar接口中的registerBeanDefinitions()方法,此…...
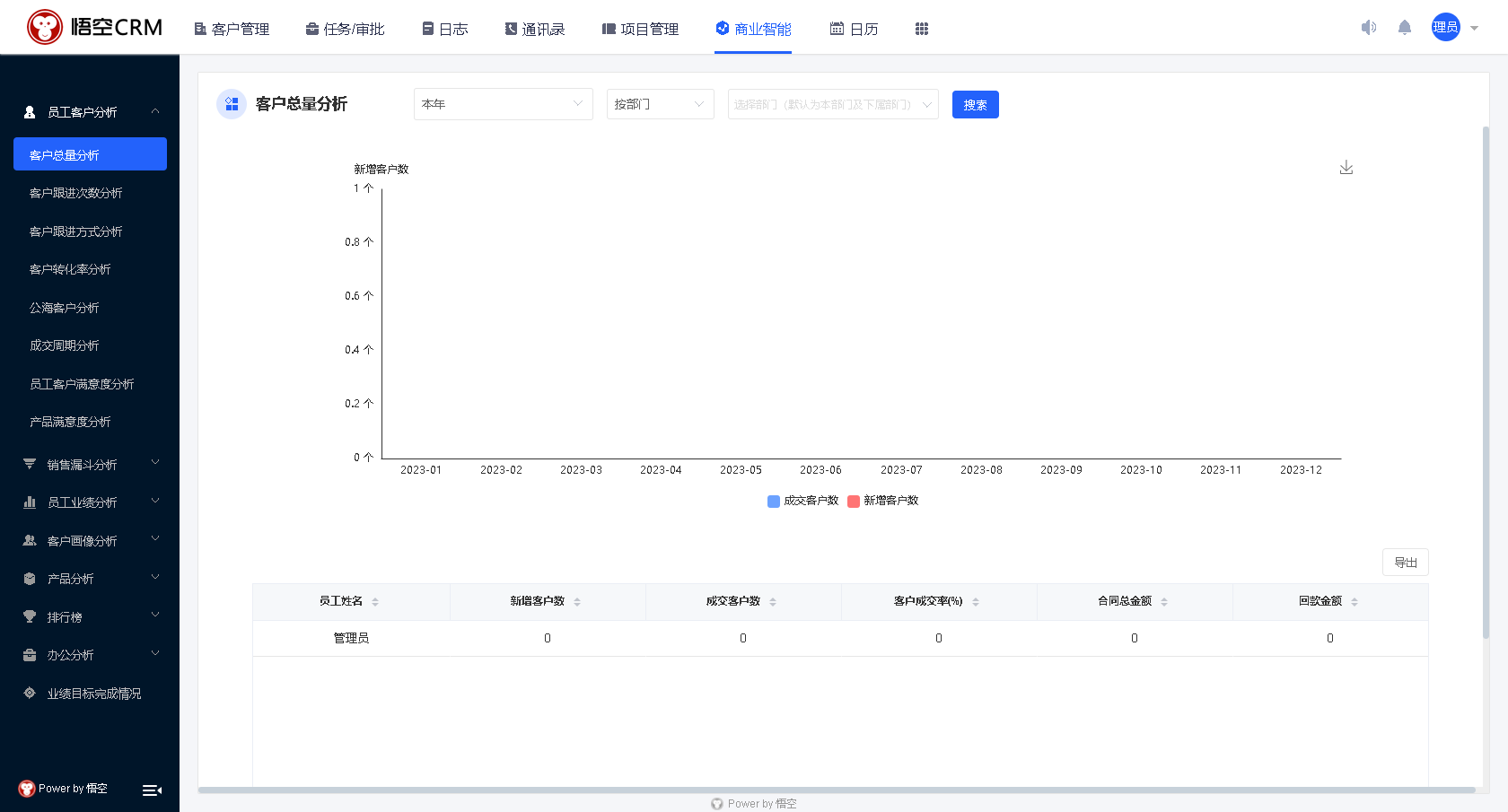
宝塔搭建实战php悟空CRM前后端分离源码-vue前端篇(二)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享了悟空CRM server端在宝塔部署的方式,但是由于前端是用vue开发的,如果要额外开发新的功能,就需要在本地运行、修改、打包重新发布到宝塔才能实现功能更新&…...
FastASR+FFmpeg(音视频开发+语音识别)
想要更好的做一件事情,不仅仅需要知道如何使用,还应该知道一些基础的概念。 一、音视频处理基本梳理 1.多媒体文件的理解 1.1 结构分析 多媒体文件本质上可以理解为一个容器 容器里有很多流 每种流是由不同编码器编码的 在众多包中包含着多个帧(帧在音视…...

二分查找的实现代码JAVA
二分查找一、思路二、实现代码(普通版)三、整数溢出问题四、改进代码一、思路 1.前提: 有已排序数组A (假设已经做好) 2.定义左边界L、 右边界R,确定搜索范围,循环执行二分查找(3、4两步) 3.获取中间索引 M Floor((LR) 1/2) 4.中间素索引的值…...

cesium: 设置skybox透明并添加背景图 ( 003 )
第003个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中设置skybox透明并添加背景图。 我们不想要黑乎乎的背景,想自定义一个背景图,然后前面显示地球。 直接复制下面的 vue+cesium源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共70…...

【python】类的详解
注:最后有面试挑战,看看自己掌握了吗 文章目录PO verses OOPOOO当一个类很复杂的时候,考虑多弄一个类的改造私有类的模块化静态类verses动态类动态类查看模块源代码对象机制的基石 PyObjectPO verses OO PO PO耦合性高,很多过程…...

西安银行就业总结
引 进银行性价比最高的时刻是本科,研究生的话可以去需要研究生较多的银行,比如邮储或者证券类的中信建投。中信建投很香,要求本硕西电。研究生学历的话,一般情况下银行不会卡本科,只看最高学历,部分银行需…...

JavaScript Window
文章目录JavaScript Window浏览器对象模型 (BOM)Window 对象Window 尺寸其他 Window 方法JavaScript Window 浏览器对象模型 (BOM) 使 JavaScript 有能力与浏览器"对话"。 浏览器对象模型 (BOM) 浏览器对象模型(Browser Object Model (BOM))…...

那些开发过程中需要遵守的开发规范
入职公司三天,没干啥其他活,基本在配置本地环境和阅读相关文档。技术方面公司基本用的是主流的技术体系,入职后需要先阅读阿里的开发规范和其他的一些产研文档。今天整理一些平时需要关注的阿里规约和数据库开发规范,方便今后在开…...

EFCore 基础入门教程
一、EFCore 基础入门教程EF 框架的简介、发展历史;ORM框架概念学习地址:https://blog.csdn.net/u011127019/article/details/129212786?spm1001.2014.3001.5502EFCore 安装,引入、支持的数据库学习地址:https://www.cnblogs.com/…...
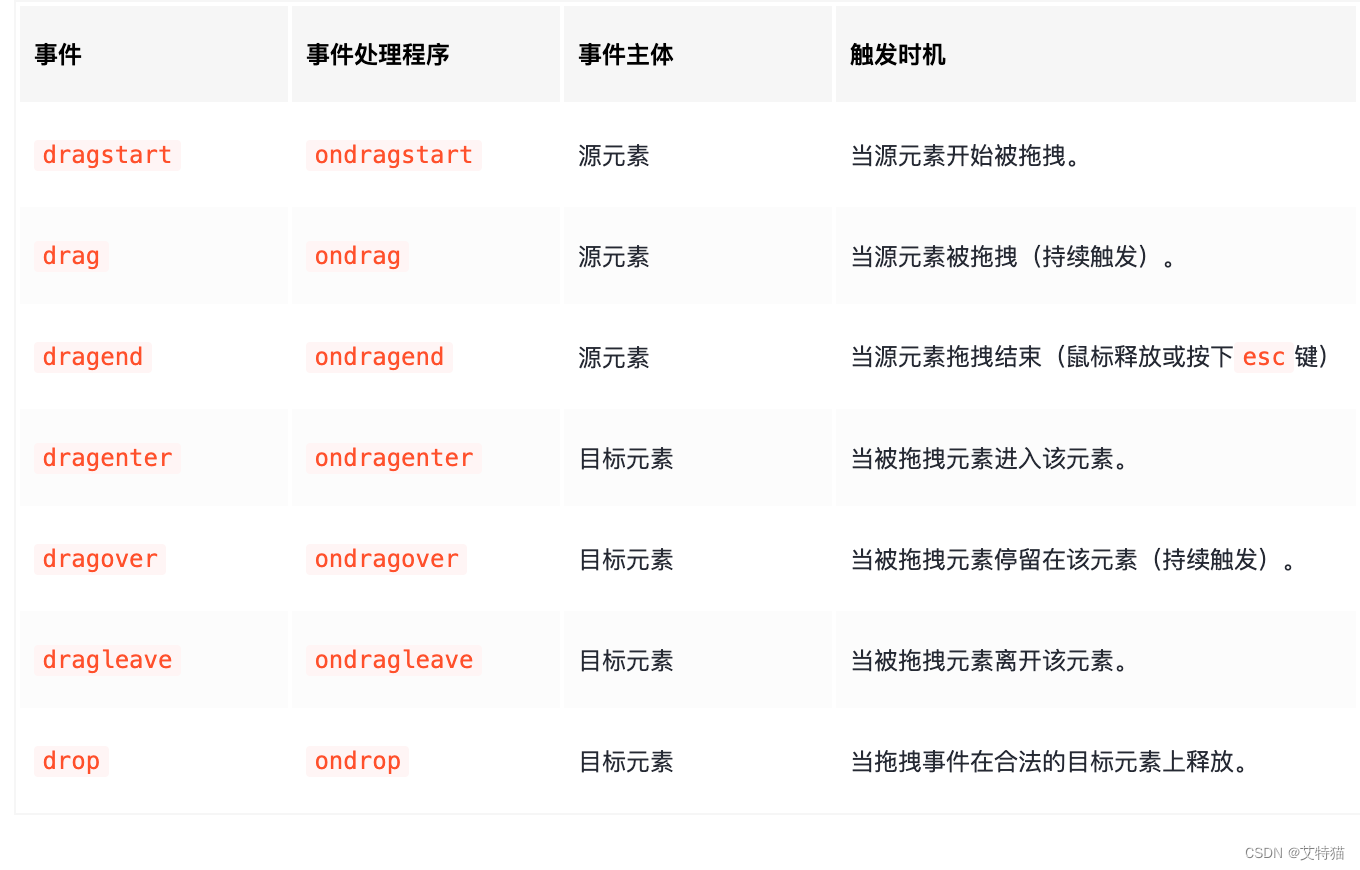
HTML5 Drag and Drop
这是2个组合事件 dom对象分源对象和目标对象 绑定的事件也是分别区分源对象和目标对象 事件绑定 事件顺序 被拖拽元素,事件触发顺序是 dragstart->drag->dragend; 对于目标元素,事件触发的顺序是 dragenter->dragover->drop/…...
惠普m1136打印机驱动程序安装教程
惠普m113打印机是一款功能强大的多功能打印机,它能够打印、复印、扫描和传真等。如果你要使用这款打印机,你需要下载并安装驱动程序,以确保它能够在你的计算机上正常工作。在本文中,我们将介绍如何下载和安装惠普m1136打印机驱动程…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
