条件期望3
条件期望例题—连续发生的事情
连续地做二项实验, 每一次成功概率为p.
当连续k次成功时, 停止实验.
求停止实验时做的总实验次数的期望.
解:
错误解法
设NkN_kNk为停止实验时做的总实验次数, 则
E[Nk]=E[E[Nk∣Nk−1]]=∑j=k−1∞E[Nk∣Nk−1=j]\begin{split} E[N_k] &= E[E[N_k|N_{k-1}]] \\ &=\sum_{j= k-1}^{\infin}E[N_k|N_{k-1}=j] \end{split} E[Nk]=E[E[Nk∣Nk−1]]=j=k−1∑∞E[Nk∣Nk−1=j]
因为
E[Nk∣Nk−1]=p⋅(NK−1+1)+(1−p)⋅E[Nk]E[N_k|N_{k-1}] = p\cdot(N_{K-1} +1) + (1-p)\cdot E[N_k] E[Nk∣Nk−1]=p⋅(NK−1+1)+(1−p)⋅E[Nk]
(一旦错了又得重开)
对两边去取期望
E[E[Nk∣Nk−1]]=E[Nk]=p⋅(E[Nk−1]+1)+(1−p)⋅E[Nk]E[E[N_k|N_{k-1}]] = E[N_k] = p \cdot (E[N_{k-1}] + 1) + (1-p) \cdot E[N_k] E[E[Nk∣Nk−1]]=E[Nk]=p⋅(E[Nk−1]+1)+(1−p)⋅E[Nk]
即
E[Nk]=E[Nk−1]+1E[N_k] = E[N_{k-1}] + 1 E[Nk]=E[Nk−1]+1
因为E[N1]=1pE[N_1] = \frac{1}{p}E[N1]=p1, 所以
E[N2]=1p+1↓E[Nn]=1p+(n−1)\begin{split} E[N_2] &= \frac{1}{p} + 1 \\ &\downarrow \\ E[N_n] &= \frac{1}{p} + (n-1) \end{split} E[N2]E[Nn]=p1+1↓=p1+(n−1)
易知上述解法的答案在直觉上是不成立的, 因为随着k的增大, E[Nk]E[N_k]E[Nk]的增长速度应该以非常快的速度增大, 而非仅仅是线性增长, 所以显然是错误的.
正确解法
E[Nk]=E[E[Nk∣Nk−1]]E[N_k] = E[E[N_k|N_{k-1}]] E[Nk]=E[E[Nk∣Nk−1]]
显然, 最要紧的是找出E[Nk∣Nk−1]E[N_k|N_{k-1}]E[Nk∣Nk−1]作为Nk−1N_{k-1}Nk−1的函数, 这个函数关系是什么
(一旦错了又得重开), 这个思路对的, 但(1)式是错的
E[Nk∣Nk−1]=p⋅(NK−1+1)+(1−p)⋅E[Nk](1)E[N_k|N_{k-1}] = p\cdot(N_{K-1} +1) + (1-p)\cdot E[N_k] \tag{1} E[Nk∣Nk−1]=p⋅(NK−1+1)+(1−p)⋅E[Nk](1)
应该是这样的思路
现在已经做了Nk−1次试验↙↘成功(概率p)失败(概率1−p)Nk=Nk−1+1Nk=Nk−1+1+Nk\begin{split} 现在已经做了&N_{k-1}次试验 \\ \swarrow&\searrow \\ 成功(概率p)\ \ \ \ \ \ &\ \ \ \ \ \ 失败(概率1-p) \\ N_k = N_{k-1} + 1\ \ \ \ \ &\ \ \ \ \ \ N_k = N_{k-1} + 1 + N_k \end{split} 现在已经做了↙成功(概率p) Nk=Nk−1+1 Nk−1次试验↘ 失败(概率1−p) Nk=Nk−1+1+Nk
所以(2)(2)(2)式才是正确的
E[Nk∣Nk−1]=p⋅(NK−1+1)+(1−p)⋅(NK−1+1+E[Nk])=NK−1+(1−p)⋅E[Nk](2)\begin{split} E[N_k|N_{k-1}] &= p\cdot(N_{K-1} +1) + (1-p)\cdot (N_{K-1} +1+E[N_k]) \\ &=N_{K-1} +(1-p)\cdot E[N_k] \tag{2} \end{split} E[Nk∣Nk−1]=p⋅(NK−1+1)+(1−p)⋅(NK−1+1+E[Nk])=NK−1+(1−p)⋅E[Nk](2)
其他的推导过程同上, 最终也是一个递归方程
E[Nk]=E[Nk−1]p+1pE[N_k] = \frac{E[N_{k-1}]}{p} + \frac{1}{p} E[Nk]=pE[Nk−1]+p1
最终的结果是
E[Nk]=1p+1p2+⋯+1pkE[N_k] = \frac{1}{p}+ \frac{1}{p^2} + \cdots + \frac{1}{p^k} E[Nk]=p1+p21+⋯+pk1
显然这一结果才是正确的结果, 直观上也更加准确.
相关文章:

条件期望3
条件期望例题—连续发生的事情 连续地做二项实验, 每一次成功概率为p. 当连续k次成功时, 停止实验. 求停止实验时做的总实验次数的期望. 解: 错误解法 设NkN_kNk为停止实验时做的总实验次数, 则 E[Nk]E[E[Nk∣Nk−1]]∑jk−1∞E[Nk∣Nk−1j]\begin{split} E[N_k] & E[E…...

第四届蓝桥杯省赛 C++ B组 - 翻硬币
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:蓝桥杯题解集合 📝原题地址:翻硬币 📣专栏定位:为想参加蓝桥杯的小伙伴整理常考算法题解,祝大家都…...

linux shell 入门学习笔记14 shell脚本+数学计算
概念 把复杂的命令执行过程,通过逻辑代码,组成一个脚本文件的方式就叫做shell脚本。 shebang #! /bin/bash #! /bin/perl #! /bin/python执行脚本的方式 source my_first.sh . my_first.shbash my_first.sh ./my_first.sh变量引用 ${var} 取出变量结果 …...

ESP32设备驱动-MAX30100心率监测传感器驱动
MAX30100心率监测传感器驱动 1、MAX30100介绍 MAX30100 是一款集成脉搏血氧饱和度和心率监测传感器解决方案。 它结合了两个 LED、一个光电探测器、优化的光学器件和低噪声模拟信号处理,以检测脉搏血氧饱和度和心率信号。 MAX30100 采用 1.8V 和 3.3V 电源供电,可通过软件…...
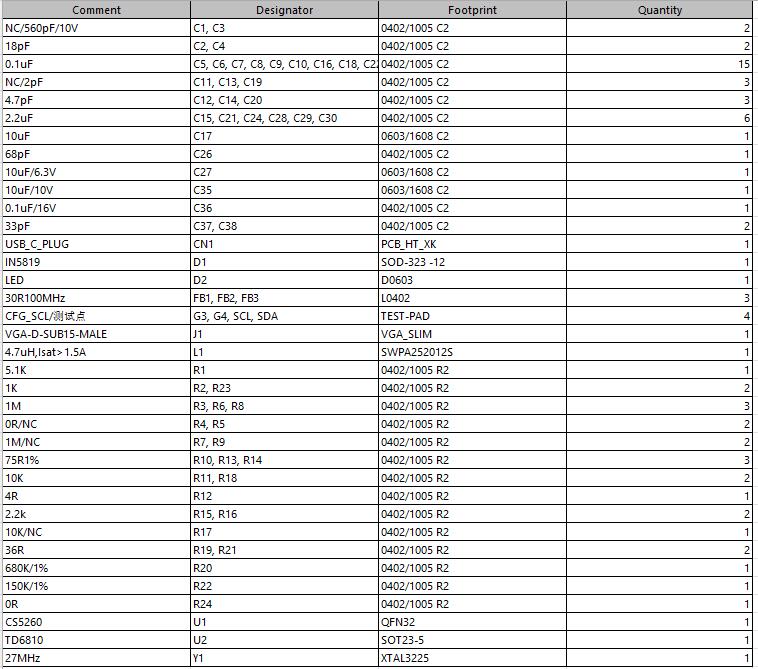
RTD2169芯片停产|完美替代RTD2169芯片|CS5260低BOM成本替代RTD2169方案设计
RTD2169芯片停产|完美替代RTD2169芯片|CS5260低BOM成本替代RTD2169方案设计 瑞昱的RTD2169芯片目前已经停产了, 那么之前用RTD2169来设计TYPEC转VGA方案的产品,该如何生产这类产品?且RTD2169芯片价格较贵,芯片封装尺寸是QFN40&…...

urho3d数据库
只有在启用以下两个构建选项之一时,数据库子系统才会构建到Urho3D库中:Urho3D_Database_ODBC和Urho3D-Database_SQLITE。当两个选项都启用时,URHO3D_DATABASE_ODBC优先。这些构建选项决定子系统将使用哪个数据库API。ODBC DB API更适用于本地…...

141. 周期
Powered by:NEFU AB-IN Link 文章目录141. 周期题意思路代码141. 周期 题意 一个字符串的前缀是从第一个字符开始的连续若干个字符,例如 abaab 共有 5个前缀,分别是 a,ab,aba,abaa,abaab。 我们希望知道一…...

Windows下命令执行绕过技巧总结(渗透测试专用)
一、连接符1、双引号不要求双引号闭合举例:"who"a"mi" //闭合的 "who"a"mi //不闭合的2、圆括号必须在两边,不能包括中间的字符。举例:((whoami))3、^符号(转译符号)不可以在结尾&…...
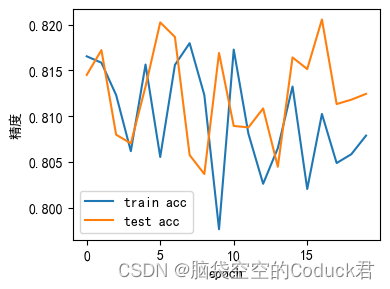
mindspore的MLP模型(多层感知机)
导入模块 import hashlib import os import tarfile import zipfile import requests import numpy as np import pandas as pd import mindspore import mindspore.dataset as ds from mindspore import nn import mindspore.ops as ops import mindspore.numpy as mnp from …...

【论文极速读】VQ-VAE:一种稀疏表征学习方法
【论文极速读】VQ-VAE:一种稀疏表征学习方法 FesianXu 20221208 at Baidu Search Team 前言 最近有需求对特征进行稀疏编码,看到一篇论文VQ-VAE,简单进行笔记下。如有谬误请联系指出,本文遵循 CC 4.0 BY-SA 版权协议,…...

Flask-Blueprint
Flask-Blueprint 一、简介 概念: Blueprint 是一个存储操作方法的容器,这些操作在这个Blueprint 被注册到一个应用之后就可以被调用,Flask 可以通过Blueprint来组织URL以及处理请求 。 好处: 其本质上来说就是让程序更加松耦合…...

png图片转eps格式
下载latex工具后 在要转换的png图片文件夹路径下,打开命令行窗口,输入以下命令: bmeps -c fig图片名.png 图片名.eps...

English Learning - L2 语音作业打卡 Day2 2023.2.23 周四
English Learning - L2 语音作业打卡 Day2 2023.2.23 周四💌 发音小贴士:💌 当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音[ ɔ: ]&…...

低频量化之 可转债 配债 策略数据 - 全网独家
目录历史文章可转债配债数据待发转债(进展统计)待发转债(行业统计)待发转债(5证监会通过,PE排序)待发转债(5证监会通过,安全垫排序)待发转债(4发审…...

论文阅读_DALLE-2的unCLIP模型
论文信息 name_en: Hierarchical Text-Conditional Image Generation with CLIP Latents name_ch: 利用CLIP的层次化文本条件图像生成 paper_addr: http://arxiv.org/abs/2204.06125 doi: 10.48550/arXiv.2204.06125 date_read: 2023-02-12 date_publish: 2022-04-12 tags: [‘…...

软件测试5年,历经3轮面试成功拿下华为Offer,24K/16薪不过分吧
前言 转眼过去,距离读书的时候已经这么久了吗?,从18年5月本科毕业入职了一家小公司,到现在快5年了,前段时间社招想着找一个新的工作,前前后后花了一个多月的时间复习以及面试,前几天拿到了华为的…...

【软件工程】课程作业(三道题目:需求分析、概要设计、详细设计、软件测试)
文章目录:故事的开头总是极尽温柔,故事会一直温柔……💜一、你怎么理解需求分析?1、需求分析的定义:2、需求分析的重要性:3、需求分析的内容:4、基于系统分析的方法分类:5、需求分析…...
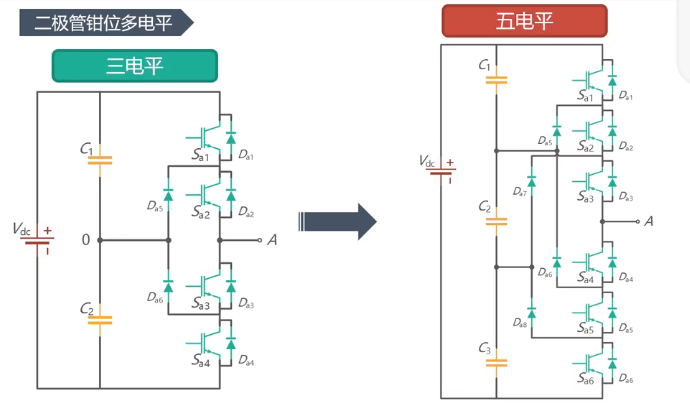
05 DC-AC逆变器(DCAC Converter / Inverter)简介
文章目录0、概述逆变原理方波变换阶梯波变换斩控调制方式逆变器分类逆变器波形指标1、方波变换器A 单相单相全桥对称单脉冲调制移相单脉冲调制单相半桥2、方波变换器B 三相180度导通120度导通(线、相的关系与180度相反)3、阶梯波逆变器独立直流源二极管钳…...

带你深层了解c语言指针
前言 🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻推荐专栏: 🍔🍟🌯 c语言进阶 🔑个人信条: 🌵知行合一 🍉本篇简介:>:介绍c语言中有关指针更深层的知识. 金句分享: ✨今天…...
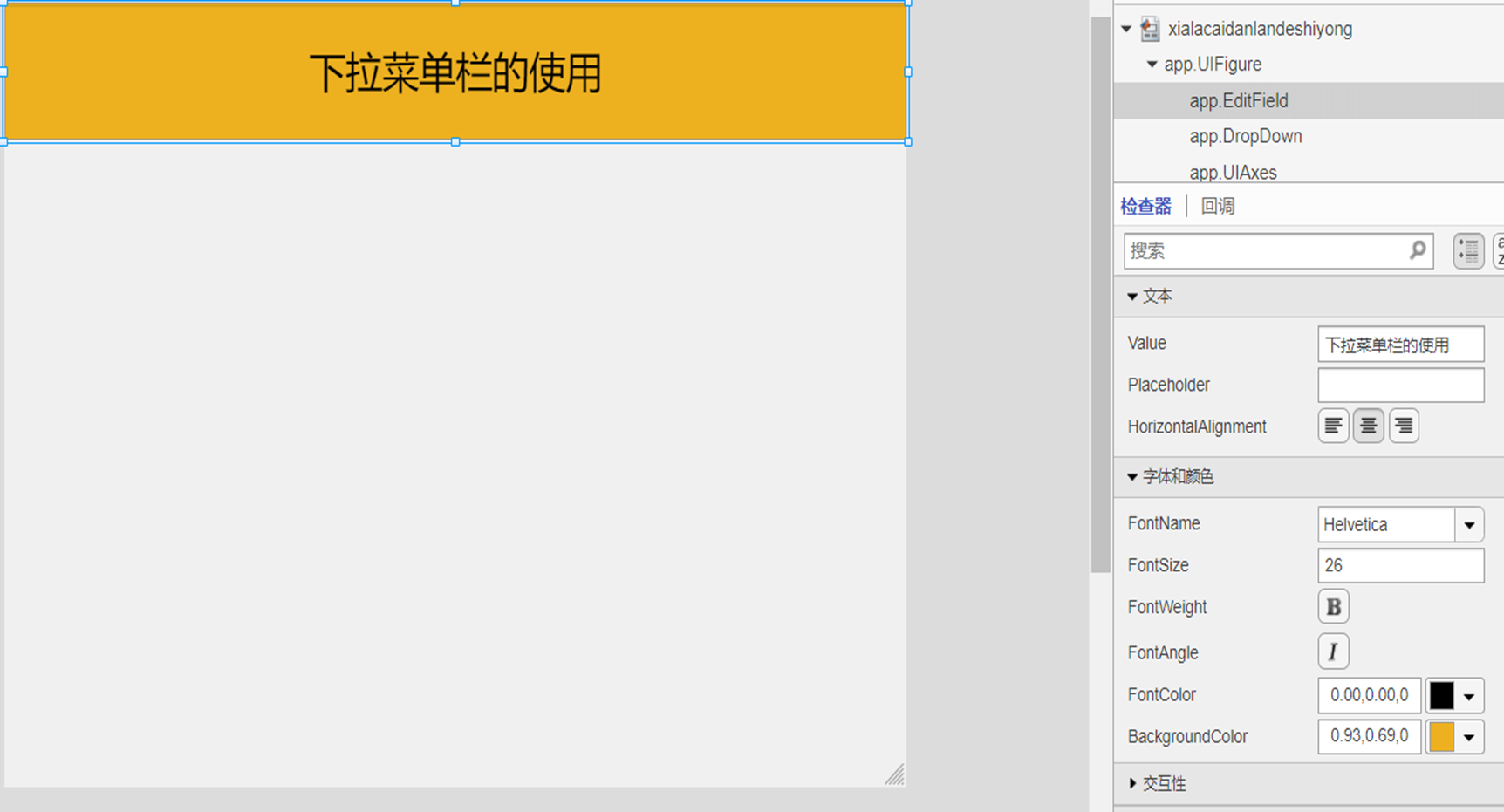
2-MATLAB APP Design-下拉菜单栏的使用
一、APP 界面设计展示 1.新建一个空白的APP,在此次的学习中,我们会用到编辑字段(文本框)、下拉菜单栏、坐标区,首先在界面中拖入一个编辑字段(文本框),在文本框中输入内容:下拉菜单栏的使用,调整背景颜色,字体的颜色为黑色,字体的大小调为26. 2.在左侧组件库常用栏…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
