管理类联考——数学——汇总篇——知识点突破——数据分析——记忆
文章目录
- 考点
- 记忆/考点汇总——按大纲
- 整体
- 目录大纲法
- 记忆宫殿法
- 绘图记忆法
- 局部
- 数字编码法
- 对号不对号
- 归类记忆法
- 重点记忆法
- 歌决记忆法
- 口诀:加法分类,类类相加;乘法分步,步步相乘。
- 谐音记忆法
- 涂色
- 理解记忆法
- 比较记忆法
- 转图像记忆法
本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多,通常使用记忆宫殿法,绘图记忆法进行记忆,针对局部/细节/组成的部分,可通过多种方法,比如联想记忆法、理解记忆法等进行进一步记忆。
考点
通过汇总各方大佬资料,作为收集考点/记忆点的信息输入:XX,收集汇总如下:
汇总考点的必要,或者说,汇总记忆的内容的必要,不言而喻,首先,你要记忆东西,得有东西,所以你要梳理出你需要记忆的全部东西,其次,在收集多个大佬的梳理的考点,又可以找出各条逻辑帮助记忆考点,所以,梳理考点是很有必要的,是记忆的基础,是记忆宫殿里面的物品,是我们最后考试需要去找到的解题物品。
记忆/考点汇总——按大纲
——加减乘除原理——
+加法原理:分类计数原理:如果完成一件事有n类办法,只要选择其中一类办法中的任何一种方法,就可以完成这件事。若第一类办法中有 m 1 m_1 m1种不同的方法,第二类办法中有 m 2 m_2 m2种不同的方法…第n类办法中有 m n m_n mn种不同的办法,那么完成这件事共用 N = m 1 + m 2 + . . . + m n N=m_1+m_2+...+m_n N=m1+m2+...+mn种不同的方法。
×乘法原理:分步计数原理:如果完成一件事,必须依次连续地完成n个步骤,这件事才能完成。若完成第一个步骤有 m 1 m_1 m1种不同的方法,完成第二个步骤有 m 2 m_2 m2种不同的方法……完成第n个步骤有 m n m_n mn种不同的方法,那么完成这件事共有 N = m 1 ∗ m 2 ∗ . . . . . . ∗ m n N= m_1*m_2*......*m_n N=m1∗m2∗......∗mn种不同的方法。——【不同类的方法(其中每一种方法都能把事情从头至尾做完)数之间做加法,不同步的方法(其中每一种方法都只能完成这件事的一部分)数之间做乘法】
-减法原理:正面难则反着做(“ − - −”号):当出现“至少、至多”、“否定用语"等正面较难分类的题目,可以采用反面进行求解,注意部分反面的技巧以及“且、或"的反面用法。
÷除法原理:看到相同,定序用除法消序( “ ÷ " “÷" “÷"号): ÷ ÷ ÷号的用法就在于消序,当题目需要消除顺序的时候,就是 ÷ ÷ ÷号登场的时候。
(1)部分相同、定序;(2)环排;(3)分组;
(1)定序问题:当把某n个元素进行排序时,其中m个元素不计顺序或者顺序已定,要把这m个元素的顺序除掉,有多少除多少,定序公式: n ! m ! \frac{n!}{m!} m!n!
(3)分组问题:
①均匀分组:分步取,得组合数相乘,再除以组数的阶乘,即除法处理。
②非均匀分组:分步取,得组合数相乘,即组合处理。
③混合分组:分步取,得组合数相乘,再除以均匀分组的组数的阶乘。
——排列组合——
1.排列与组合的推导:
从n个不同的元素中取出m(m≤n)个元素做排列为 A n m A_n^m Anm,事实上可以分为两个步骤:
第一步:从n个不同的元素中取出m(m≤n)个元素做组合为 C n m C_n^m Cnm;
第二步:将这m个元素做全排列为 m ! m! m!,从而我们有 A n m = C n m ⋅ m ! = C n m ⋅ A m m A_n^m=C_n^m·m!=C_n^m·A_m^m Anm=Cnm⋅m!=Cnm⋅Amm,即 C n m = A n m m ! C_n^m=\frac{A_n^m}{m!} Cnm=m!Anm
2. 排列是先组合再排列:
A n m = C n m ⋅ A m m = C n m ⋅ m ! A_n^m=C_n^m·A_m^m=C_n^m·m! Anm=Cnm⋅Amm=Cnm⋅m!,故 A n m A_n^m Anm可由组合 C n m C_n^m Cnm与阶乘 m ! m! m!代替。
3. 排列与组合的区别:
口诀:与序无关是组合,要求有序是排列。——【】
4. 解题准则:
(1)排列 A n m = C n m ⋅ A m m = C n m ⋅ m ! A_n^m=C_n^m·A_m^m=C_n^m·m! Anm=Cnm⋅Amm=Cnm⋅m!,故排列是先组合再排列,即 A n m A_n^m Anm可由组合 C n m C_n^m Cnm与阶乘 m ! m! m!代替,为思路清晰,采用 C n m C_n^m Cnm与 m ! m! m!表达。
(2)选取元素或位置,用组合 C n m C_n^m Cnm。
(3)排序用阶乘 m ! m! m!。
(4)将所有的题目拆解为“选取”和“排序”的过程,然后再对应写表达式。
5. 排列问题与组合问题对比:
若从n个元素中取m个,需要考虑m的顺序,则为排列问题,用 A n m A_n^m Anm表示;
若从n个元素中取m个,无须考虑m的顺序,则为组合问题,用 C n m C_n^m Cnm表示。
6. 排列数与组合数的含义对比:
(1)排列数A的含义:先挑选再排列,有序(元素之间互换位置,结果不同)。
(2)组合数C的含义:挑选、组合,无序(元素之间互换位置,结果不变)。
排列
从n个不同元素中,任意取出m(m≤n)个元素,按照一定顺序排成一列,称为从n个不同元素中取出m个元素的一个排列。 ⟹ \Longrightarrow ⟹排列
从n个不同元素中,取出m个元素(m≤n)的所有排列的种数,称为从n个元素中取出m个元素的排列数,记作 A n m A_n^m Anm。 ⟹ \Longrightarrow ⟹ A n m A_n^m Anm称为排列数
当m=n时,即从n个不同元素中取出n个元素的排列,称为n个元素的全排列,记作 A n n A_n^n Ann,也称为n的阶乘,用符号 n ! n! n!表示。 ⟹ \Longrightarrow ⟹ n ! n! n!称为n的阶乘
A n m = n ( n − 1 ) ( n − 2 ) . . . ( n − m + 1 ) = n ! ( n − m ) ! A_n^m=n(n-1)(n-2)...(n-m+1)=\frac{n!}{(n-m)!} Anm=n(n−1)(n−2)...(n−m+1)=(n−m)!n! ⟹ \Longrightarrow ⟹ A n m A_n^m Anm称为排列数
A n n = n ( n − 1 ) ( n − 2 ) . . . 2 ⋅ 1 = n ! A_n^n=n(n-1)(n-2)...2·1=n! Ann=n(n−1)(n−2)...2⋅1=n! ⟹ \Longrightarrow ⟹ n ! n! n!称为n的阶乘/全排列
A n n − 1 = A n n = n ! A_n^{n-1}=A_n^n=n! Ann−1=Ann=n!
A n m ≠ A n n − m A_n^m≠A_n^{n-m} Anm=Ann−m
A n 1 = n A_n^1=n An1=n
A n 0 = 1 A_n^0=1 An0=1
0 ! = 1 0!=1 0!=1、 1 ! = 1 1!=1 1!=1、 2 ! = 2 2!=2 2!=2、 3 ! = 6 3!=6 3!=6、 4 ! = 24 4!=24 4!=24、 5 ! = 120 5!=120 5!=120 ⟹ \Longrightarrow ⟹常用数值——【】
组合
从n个不同元素中,任意取出m(m≤n)个元素并为一组,叫作从n个不同元素中取出m个元素的一个组合 ⟹ \Longrightarrow ⟹组合
从n个不同元素中,取出m(m≤n)个元素的所有组合的个数、称为从n个不同元素中取出m个元素的组合数,记作 C n m C_n^m Cnm ⟹ \Longrightarrow ⟹ C n m C_n^m Cnm称为组合数
C n m = A n m A m m = n ( n − 1 ) . . . ( n − m + 1 ) m ( m − 1 ) . . . ⋅ 2 ⋅ 1 = n ! m ! ( n − m ) ! = A n m m ! C_n^m=\frac{A_n^m}{A_m^m}=\frac{n(n-1)...(n-m+1)}{m(m-1)...·2·1}=\frac{n!}{m!(n-m)!}=\frac{A_n^m}{m!} Cnm=AmmAnm=m(m−1)...⋅2⋅1n(n−1)...(n−m+1)=m!(n−m)!n!=m!Anm,则 A n m = C n m ⋅ m ! A_n^m=C_n^m·m! Anm=Cnm⋅m! ⟹ \Longrightarrow ⟹ C n m C_n^m Cnm称为组合数
C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m ⟹ \Longrightarrow ⟹组合数性质:对称性
等式特点:等式两边下标同,上标之和等于下标:如 C 9 6 = C 9 3 = 9 × 8 × 7 3 ! = 84 C_9^6=C_9^3=\frac{9×8×7}{3!}=84 C96=C93=3!9×8×7=84 ,此性质作用:当 m > n 2 m>\frac{n}{2} m>2n时,计算 C n m C_n^m Cnm可变为计算 C n n − m C_n^{n-m} Cnn−m,能够使运算简化。
C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m ,可得: C n x = C n y C_n^x=C_n^y Cnx=Cny ⟹ \Longrightarrow ⟹ x = y 或 x + y = n x=y或x+y=n x=y或x+y=n(易遗忘此种情况),其中,x,y均为非负整数
C n m = C n − 1 m − 1 + C n − 1 m C_n^m=C_{n-1}^{m-1}+C_{n-1}^{m} Cnm=Cn−1m−1+Cn−1m ⟹ \Longrightarrow ⟹组合数性质:递推公式
C n − 1 m − 1 C n m = m m \frac{C_{n-1}^{m-1}}{C_n^m}=\frac{m}{m} CnmCn−1m−1=mm
n ! = n × ( n − 1 ) ! n!=n×(n-1)! n!=n×(n−1)!
( n + 1 ) × n ! = ( n + 1 ) ! (n+1)×n!=(n+1)! (n+1)×n!=(n+1)!
n × n ! = [ ( n + 1 ) − 1 ] × n ! = ( n + 1 ) × n ! − n ! = ( n + 1 ) ! − n ! n×n!=[(n+1)-1]×n!=(n+1)×n!-n!=(n+1)!-n! n×n!=[(n+1)−1]×n!=(n+1)×n!−n!=(n+1)!−n!
n ( n + 1 ) ! = n + 1 − 1 ( n + 1 ) ! = n + 1 ( n + 1 ) ! − 1 ( n + 1 ) ! = 1 n ! − 1 ( n + 1 ) ! \frac{n}{(n+1)!}=\frac{n+1-1}{(n+1)!}=\frac{n+1}{(n+1)!}-\frac{1}{(n+1)!}=\frac{1}{n!}-\frac{1}{(n+1)!} (n+1)!n=(n+1)!n+1−1=(n+1)!n+1−(n+1)!1=n!1−(n+1)!1 ⟹ \Longrightarrow ⟹组合数性质
C n 0 + C n 1 + C n 2 + . . . + C n n = 2 n C_n^0+C_n^1+C_n^2+...+C_n^n=2^n Cn0+Cn1+Cn2+...+Cnn=2n
C n 0 + C n 2 + C n 4 + . . . = 2 n − 1 C_n^0+C_n^2+C_n^4+...=2^{n-1} Cn0+Cn2+Cn4+...=2n−1
C n 1 + C n 3 + C n 5 + . . . = 2 n − 1 C_n^1+C_n^3+C_n^5+...=2^{n-1} Cn1+Cn3+Cn5+...=2n−1 ⟹ \Longrightarrow ⟹组合恒等式
C n 0 = C n n = 1 C_n^0=C_n^n=1 Cn0=Cnn=1
C n 1 = C n n − 1 = n − 1 C_n^1=C_n^{n-1}=n-1 Cn1=Cnn−1=n−1
C 3 2 = C 3 1 = 3 C_3^2=C_3^1=3 C32=C31=3
C 5 2 = C 5 3 = 10 C_5^2=C_5^3=10 C52=C53=10
C 6 2 = C 6 4 = 15 C_6^2=C_6^4=15 C62=C64=15 ⟹ \Longrightarrow ⟹常用组合数
——奇技——
一个位置一个元素
(1)先特殊后一般
先处理特殊元素或位置,再处理一般元素或位置。
(2)相邻、不相邻问题
相邻用捆绑打包法;不相邻用插空法;当相邻问题与不相邻问题同时出现在题干
中,需要按照先解决相邻再解决不相邻问题的顺序来求解。
一个位置多个元素(观察元素与对象采用不同策略)
分房问题特征:
(1)1个房间可容纳多个人;(2)每个人都只能去一间房。
①元素不同,对象不同,对元素无限定,则可重复使用——用方幂法;
②元素不同,对象不同,对元素有限定,元素与对象有对应关系——用对号不对号;
③元素不同,对象不同,对元素有限定,分组中有同样的数量——先分堆后分配;
④元素不同,对象相同——只分堆,不分配;
⑤元素相同,对象不同——先满足后隔板;
⑥元素相同,对象相同———穷举,列举法。
相邻与不相邻
相邻问题采用捆绑法:将相邻的几个元素捆绑看成一个大元素,再与其余普通元素进行排列,注意不要忘记这个捆绑后的大元素内部需要排序。
不相邻问题采用插空法:先排好其余元素,再将不相邻的元素插入空位。
分房问题
适用条件:元素不同,对象不同,对元素无限定,则可重复使用。
表现形式:不同的元素无限制地进入到不同的位置。
前提条件:每个元素只能进人一个位置,但是每个位置可以容纳多个元素。
注意事项:解决“允许重复排列问题”要注意区分两类元素:一类元素可以重复,另一类不能重复。把不能重复的元素看作“人”,能重复的元素看作“房”,再利用乘法原理直接求解的方法称为“分房法”。一般地n个不同的元素没有限制地安排在m个位置上的排列数为 m n m^n mn种。
解决办法:n个不同的元素无限制地进入m个不同的位置有 m n m^n mn种方法。一共有“ 可重复元 素 不可重复元素 可重复元素^{不可重复元素} 可重复元素不可重复元素”种情况,即“可重复元素”为底数,“不可重复元素”为指数。
方法应用:n个人/不同的球/不同的信去m个不同房间/不同盒子/不同邮筒,有 m n m^n mn种方法。
广义的分房问题
要求:n个不同元素分给m个不同对象且所有元素全部分完
模型1:无限制条件的分房问题:任意分(容许有对象没分到):方幂法,共有 m n m^n mn种
模型2:有限制条件的分房问题:有限制条件分(每个对象至少分1个):先分堆再分配
对号与不对号:无论几个元素,只要对号安排,都只有1种方法。
不对号安排记答案:2个不对号有1种方法;3个不对号有2种方法;4个不对号有9种方法;5个不对号有44种方法。
隔板法
适用条件:(1)元素相同;(2)对象不同;(3)每个对象至少分到1个。
方法原理:由于物品相同,每个对象仅以分到的数量来进行区分,所以通过隔板调整分配的数量,故隔板有几种放法就表示有几种分法。
使用要求:①n个元素要相同;②m个分配对象不同。
公式公式:如果分配对象非空,即每个对象至少分一个,则有 C n − 1 m − 1 C_{n-1}^{m-1} Cn−1m−1种;如果分配对象允许空,则有 C n + m − 1 m − 1 C_{n+m-1}^{m-1} Cn+m−1m−1种。——【理解记忆法:将n个相同元素摆成一排,它们之间有 n − 1 n-1 n−1个空位,插入 m − 1 m-1 m−1块隔板就可以分成m份,所以公式为 C n − 1 m − 1 C_{n-1}^{m-1} Cn−1m−1。如果分配对象允许空,此时将元素看成 m + n m+n m+n个,再用隔板法,则有 C n + m − 1 m − 1 C_{n+m-1}^{m-1} Cn+m−1m−1种。】——【理解记忆法:将n个相同的元素全分给m个对象,每个对象至少分1个。:把这n个元素排成一排,中间有n-1个空,挑出m-1个空放上挡板,自然就分成了m组,所以分法一共有 C n − 1 m − 1 C_{n-1}^{m-1} Cn−1m−1种;将n个相同的元素全分给m个对象,每个对象至少分0个元素(即可以为空)。:增加m个元素(m为对象的个数),此时一共有n+m个元素,中间形成n+m-1个空,选出m-1个空放上挡板即可,共有 C n + m − 1 m − 1 C_{n+m-1}^{m-1} Cn+m−1m−1种方法。】
n个不同元素作圆形排列,坐成圆形没有首尾之分,所以固定一人,共有 ( n − 1 ) ! (n-1)! (n−1)!种排法。如果从n个不同元素中取出m个元素作圆形排列共有 1 m C n m \frac{1}{m}C_n^m m1Cnm 。
分组分配
(1)不同元素分组问题:
① 解题方法:如果出现m个小组没有任何区别,则需要消序,除以 A m m A_m^m Amm,其他情况的分组不需要消序。
② 技巧总结:1)小组无名称,分组之后需要考虑消序,其中小组人数相同,则需要消序;小组人数不同,不需要消序。2)小组有名称,按要求分组之后不需要考虑消序。
(2)不同元素分配问题:
① 解题方法:先分组(注意消序),再分配(排列)
② 技巧总结:按“先分组,再分配”的顺序求解,分组时注意人数相同的小组需要消序。
(3)相同元素分配问题:
①相同元素分配不同对象至少分1个:
解题方法:挡板法:把n个相同元素排成一排,中间只有 n − 1 n-1 n−1个空,从中放 m − 1 m-1 m−1个挡板,故一共有 C n − 1 m − 1 C_{n-1}^{m-1} Cn−1m−1种分法。
②可以为0型:
解题方法:增加元素法:增加m个元素(m为对象的个数),使每个对象至少分得1个元素,满足了挡板法使用的条件,分法共 C n + m − 1 m − 1 C_{n+m-1}^{m-1} Cn+m−1m−1种。
④可以为多型:
解题方法:减少元素法:使每个对象至少分得1个元素,再使用挡板法。
分堆
指定数量的分堆:按照所给每堆的数量要求进行分堆,注意有几堆数量相同,就要除以几的阶乘,来进行消序。
未指定数量的分堆:如果数量没有指定,则需要先根据数量分类,然后再按照每堆的数量要求进行分堆,注意有几堆数量相同,就要除以几的阶乘,来进行消序。
指定元素的分堆:如果在分堆时,有特殊要求元素,则先安排特殊要求的元素,再选其他没有要求的元素.注意特殊要求元素所在的组不用考虑消序。
分配问题:当出现不同的归属对象时,转化为分配问题。分配问题包括两个过程:先分堆,再配送。也就是先按照数量分好堆,再排序。
特殊元素分配
元素定序:先将n个元素进行全排列有 n ! n! n!种,m个元素的全排列有 m ! m! m!种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到去掉排序的作用,即若n个元素排成一列,其中m个元素次序一定,共有 n ! m ! \frac{n!}{m!} m!n!种排列方法。或者用组合法,对于定序元素,只需选位置即可,无需排序。
位置定序:在所给位置中,某些位置有大小顺序要求,直接用组合法,选好元素放位置时无需排序。
部分元素相同:在对元素排列时,出现部分元素相同(没有区别),要除以相同元素数量的阶乘,以消除排序。比如n个元素中,有k个元素相同,其他元素不同,则排序的方法数为 n ! k ! \frac{n!}{k!} k!n!。或者对于相同元素,采用组合选取位置,无需考虑顺序。
全能元素
全能元素:全能元素是指一个元素可以同时具备多个属性,在选取时,注意全能元素的归宿问题。
全能卡片:遇到全能卡片,要根据全能卡片的选中情况来分类讨论,当全能卡片选中时,要注意乘以倍数。
解题方法:对全能(特殊)元素要/不要,以及要几个进行分类讨论即可
单排环排
单排问题:
① 是且是 → 确定元素不用管,剩余元素直接排序即可;
② 是或是 → A ∪ B = A + B − A ∩ B A∪B=A+B-A∩B A∪B=A+B−A∩B;
③ 否且否 → 反面分析法:总情况数 − - −是或是;
④ 否或否 → 反面分析法:总情况数 − - −是且是。
环排公式:(1)若n个人围着一张圆桌坐下,共有 ( n — 1 ) ! (n—1)! (n—1)!种坐法;(2)若从n个人中选出m个人围着一张圆桌坐下,共有 C n m C_n^m Cnm· ( m − 1 ) ! (m-1)! (m−1)!= 1 m ⋅ A n m \frac{1}{m} ·A_n^m m1⋅Anm种坐法。
——XX——
古典概型: P ( A ) = 事件 A 包含的基本事件数 k 样本空间中基本事件总数 n P(A)=\frac{事件A包含的基本事件数k}{样本空间中基本事件总数n} P(A)=样本空间中基本事件总数n事件A包含的基本事件数k
独立事件: P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B),则称两事件A和B是相互独立的
伯努利公式:如果在一次试验中某事件发生的概率是p,那么在n次独立重复试验中这个事件恰好发生k次的概率为 P n ( k ) = C n k p k q n − k P_n(k)=C_n^kp^kq^{n-k} Pn(k)=Cnkpkqn−k,( k = 0 , 1 , 2 , … , n k=0,1,2,…,n k=0,1,2,…,n),其中 q = 1 − p q=1-p q=1−p。
k = n k=n k=n时,即在n次独立重复试验中事件A全部发生,概率为 P n ( n ) = C n n p n ( 1 − p ) 0 = p n P_n(n)=C_n^np^n(1-p)^0=p^n Pn(n)=Cnnpn(1−p)0=pn。
k = 0 k=0 k=0时,即在n次独立重复试验中事件A没有发生,概率为 P n ( 0 ) = C n 0 p 0 ( 1 − p ) n = ( 1 − p ) n P_n(0)=C_n^0p^0(1-p)^n=(1-p)^n Pn(0)=Cn0p0(1−p)n=(1−p)n。
独立地做一系列的伯努利试验,直到第k次试验时,事件A才首次发生的概率为 P k = ( 1 − P ) k − 1 P_k=(1-P)^{k-1} Pk=(1−P)k−1( k = 1 , 2 , . . . , n k=1,2,...,n k=1,2,...,n)。
n次独立重复试验的特征:
①试验的次数不止一次,而是多次,次数 n ≥ 1 n≥1 n≥1;
②每次试验的条件是一样的,是重复性的试验序列;
③每次试验的结果只有A与 A ‾ \overline{A} A两种(即事件A要么发生,要么不发生),每次试验相互独立,试验的结果互不影响,即各次试验中发生的概率保持不变。
方差: S 2 = 1 n [ ( x 1 − x ‾ ) 2 + ( x 2 − x ‾ ) 2 + . . . + ( x n − x ‾ ) 2 ] S^2=\frac{1}{n}[(x_1-\overline{x})^2+(x_2-\overline{x})^2+...+(x_n-\overline{x})^2] S2=n1[(x1−x)2+(x2−x)2+...+(xn−x)2],意义:方差是反映一组数据的整体波动大小的指标,它是指一组数据中各数据与这组数据的平均数的差的平方的平均数,它反映的是一组数据偏离平均值的情况。——【先平均,再求差,然后平方,最后再平均。】
简化方差: S 2 = 1 n [ ( x 1 2 + x 2 2 + . . . + x n 2 ) − n x ‾ 2 ] S^2=\frac{1}{n}[(x_1^2+x_2^2+...+x_n^2)-n\overline{x}^2] S2=n1[(x12+x22+...+xn2)−nx2]
拓展公式: S 2 = 1 n [ ( x 1 − x ‾ ) 2 + ( x 2 − x ‾ ) 2 + . . . + ( x n − x ‾ ) 2 ] = x 1 2 + x 2 2 + . . . + x n 2 n − ( x 1 + x 2 + . . . + x n n ) 2 S^2=\frac{1}{n}[(x_1-\overline{x})^2+(x_2-\overline{x})^2+...+(x_n-\overline{x})^2]=\frac{x_1^2+x_2^2+...+x_n^2}{n}-(\frac{x_1+x_2+...+x_n}{n})^2 S2=n1[(x1−x)2+(x2−x)2+...+(xn−x)2]=nx12+x22+...+xn2−(nx1+x2+...+xn)2
标准差: 方差 \sqrt{方差} 方差= S 2 \sqrt{S^2} S2,意义:方差和标准差都是用来描述一组数据波动情况的特征数,常用来比较两组数据的波动大小、方差较大的波动较大,方差较小的波动较小,方差的单位是原数据的单位平方,标准差的单位与原数据的单位相同。
如果一组数据 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn的平均数是 x ‾ \overline{x} x,方差为 S 2 S^2 S2,那么
(1)新数据 a x 1 , a x 2 , . . . , a x n ax_1,ax_2,...,ax_n ax1,ax2,...,axn的平均数是 a x ‾ a\overline{x} ax,方差为 a 2 S 2 a^2S^2 a2S2;
(2)新数据 x 1 + b , x 2 + b , … , x n + b x_1+b,x_2+b,…,x_n+b x1+b,x2+b,…,xn+b的平均数是 x ‾ + b \overline{x}+b x+b,方差为 S 2 S^2 S2;
(3)新数据 a x 1 + b , a x 2 + b , … , a x n + b ax_1+b,ax_2+b,…,ax_n+b ax1+b,ax2+b,…,axn+b的平均数是 α x ‾ + b α\overline{x}+b αx+b,方差为 a 2 S 2 a^2S^2 a2S2。
整体
整体使用记忆宫殿法和绘图记忆法等进行记忆
目录大纲法
-
计数原理
加乘原理
排列组合
一个位置一个元素
一个位置多个元素 -
数据描述
平均值
方差与标准差 -
概率
事件及其简单运算
加法公式
乘法公式
古典概型
伯努利概型
记忆宫殿法
绘图记忆法
局部
学习记忆——数学篇——汇总——顺口溜记忆法+谐音记忆法+理解记忆法+归类记忆法+重点记忆法+比较记忆法+转图像记忆法
数字编码法
学习记忆——记忆宫殿——编码——数字编码和字母编码——两位数
学习记忆——英语——字母编码
学习记忆——记忆宫殿——编码——数字编码——数字声母
对号不对号
【思路】“不对号”问题可以这样记住答案:2个元素不对号,1种方法;3个元素不对号,2种方法;4个元素不对号,9种方法;5个元素不对号,44 种方法。
21鳄鱼、32上颚、49死狗、544武器妻
鳄鱼用上颚咬死了狗,妻子用武器打死了它。
归类记忆法
数学知识有一个最显著的特点,就是系统性很强。数学知识之间有着内在的联系,我们可以按照它们的特性,恰当归类,使之条理化、系统化,组成一个便于记忆的知识网络。
重点记忆法
抓住一个重点,去推导,去联想。
歌决记忆法
口诀:加法分类,类类相加;乘法分步,步步相乘。
谐音记忆法
涂色
(1)直线涂色:简单的乘法原理。
(2)环形涂色公式:把一个环形区域分为k块,每块之间首尾相连,用s种颜色去涂,要求相邻两块颜色不同,则不同的涂色方法有
N = ( s — 1 ) k + ( s — 1 ) ( − 1 ) k N=(s—1)^k+(s—1)(-1)^k N=(s—1)k+(s—1)(−1)k,
式中,s为颜色数(记忆方法:se色),k为环形被分成的块数(记忆方法:kuai 块)。
理解记忆法
比较记忆法
转图像记忆法
学习记忆——数学篇——转图像记忆法

相关文章:

管理类联考——数学——汇总篇——知识点突破——数据分析——记忆
文章目录 考点记忆/考点汇总——按大纲 整体目录大纲法记忆宫殿法绘图记忆法 局部数字编码法对号不对号 归类记忆法重点记忆法歌决记忆法口诀:加法分类,类类相加;乘法分步,步步相乘。 谐音记忆法涂色 理解记忆法比较记忆法转图像记…...
springboot+mybatis-plus实现读写分离
shigen坚持日更的博客写手,擅长Java、python、vue、shell等编程语言和各种应用程序、脚本的开发。坚持记录和分享从业两年以来的技术积累和思考,不断沉淀和成长。 最近shigen加班也比较严重,很多天文章没有更新了,各位读者和伙伴见…...
java将list转为逗号隔开字符串,将逗号连接的字符串转成字符数组,将逗号分隔的字符串转换为List(Java逗号分隔-字符串与数组相互转换)
一、通过testList.stream().collect(Collectors.joining(",")) ,通过流转换,将list转为逗号隔开字符串 List<String> testList new ArrayList<>(); testList.add("test1"); testList.add("test2"); testList…...
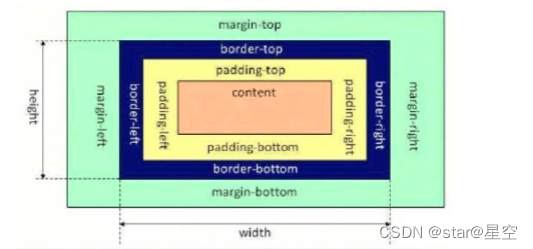
2023高频前端面试题-CSS
1. CSS 选择器的优先级是怎么样的? CSS 选择器的优先级顺序: 内联样式 > ID选择器 > 类选择器 > 标签选择器 优先级的计算: 优先级是由 A、B、C、D 四个值来决定的,具体计算规则如下 A{如果存在内联样式则为 1&…...

我会在以下情况用到GPT
ChatGPT可以在各种情况下派上用场,包括但不限于以下情况: 获取信息:你可以使用ChatGPT来获取关于各种主题的信息,例如历史事件、科学知识、文化背景等。ChatGPT可以用作一个知识库,回答你的问题。 学习新知识…...
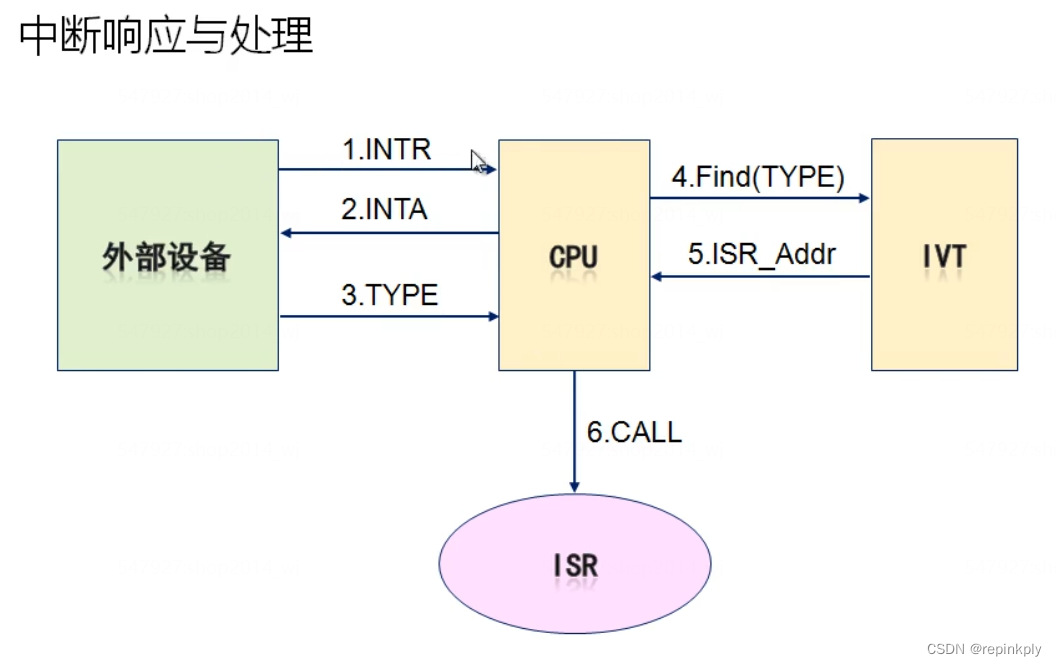
33:深入浅出x86中断机制
背景 我们知道使用0x10号中断,可以在屏幕上打印一个字符。 问题 系统中的 中断 究竟是什么? 生活中的例子 来看一个生活中例子: 小狄的工作方式 在处理紧急事务的时候,不回应同事的技术求助。老板的召唤必须回应,…...
)
docker docker-compose安装(centos7)
docker安装 1.卸载旧版 卸载旧版 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine2.安装一个yum工具 yum install -y yum-utils3.配置docker的yum源 yum-config-manager -…...

Dockerfile文件详细教程
写在前面 Dockerfile是用来构建镜像的,他实际上就是把在linux下的命令操作写到了Dockerfile中,通过Dockerfile去执行设置好的操作命令,保证通过Dockerfile的构建镜像是一致的。 实战分析 该例子来自于 chromium 项目 主要干的事情…...

机器学习-模型评估与选择
文章目录 评估方法留出法交叉验证自助法 性能的衡量回归问题分类问题查准率、查全率与F1ROC与AUC 在机器学习中,我们通常面临两个主要问题:欠拟合和过拟合。欠拟合指模型无法在训练数据上获得足够低的误差,通常是因为模型太简单,无…...

分享一下办公自动化常用的思想
目录 网页获取数据需求①大体思路:PythonseleniumXpath 网页获取数据需求②大体思路:requests爬虫 批量生成需求①文件的移动、重命名②word、Excel批量生成 匹配需求 网页获取数据需求① 大体思路:PythonseleniumXpath 我们在利用Python做…...

mac vscode 使用 clangd
C 的智能提示 IntelliSense 非常不准,我们可以使用 clangd clangd 缺点就是配置繁琐,优点就是跳转和提示代码精准 开启 clangd 之后会提示你关闭 IntelliSense 1、安装插件 clangd 搜索第一个下载多的就是 2、配置 clangd 可执行程序路径 clangd 插…...
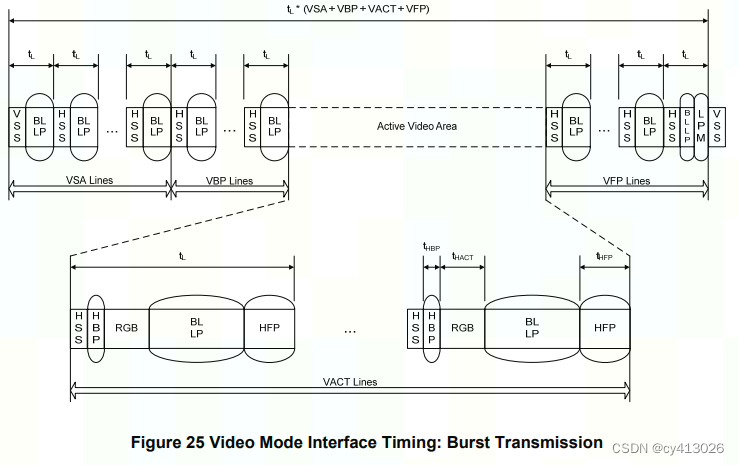
DSI及DPHY的学习
DSI的物理层PHY只能是DPHY 本节讲述的DSI是V1.02.00---2010.6.28 从DSI V1.02开始DSI支持图像数据包RGB和YCbCr的传输,在此版本之前只支持RGB传输。 本节内容与CSICDPHY相同时 请参考: CSI2与CDPHY学习-CSDN博客 同时本节会做一些与CSICDPHY的比较 …...

环形链表(C++解法)
题目 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置&#…...

星闪技术 NearLink 一种专门用于短距离数据传输的新型无线通信技术
本心、输入输出、结果 文章目录 星闪技术 NearLink 一种专门用于短距离数据传输的新型无线通信技术前言星闪技术 NearLink 的诞生背景星闪技术 NearLink 简介星闪技术 NearLink 技术是一种蓝牙技术吗星闪技术 NearLink 优势星闪技术 NearLink 应用前景弘扬爱国精神星闪技术 Nea…...

【Python机器学习】零基础掌握RandomForestRegressor集成学习
如何预测房价是不是一直困扰着大家?特别是在房地产市场波动不定的情况下,这样的预测可以说是切实需要。 要解决这个问题,一个可行的方法是利用历史房价数据和房屋的各种属性(如面积、楼层、地理位置等)进行分析。通过这些数据,可以用一个模型来预测未来房价。 假设有以…...

FreeRTOS深入教程(任务创建的深入和任务调度机制分析)
文章目录 前言一、深入理解任务的创建二、任务的调度机制1.FreeRTOS中任务调度的策略2.FreeRTOS任务调度策略实现的核心3.FreeRTOS内部链表源码解析4.如何通过就绪链表管理任务的执行顺序 三、一个任务能够运行多久1.高优先级任务可抢占低优先级任务一直运行2.相同优先级的任务…...
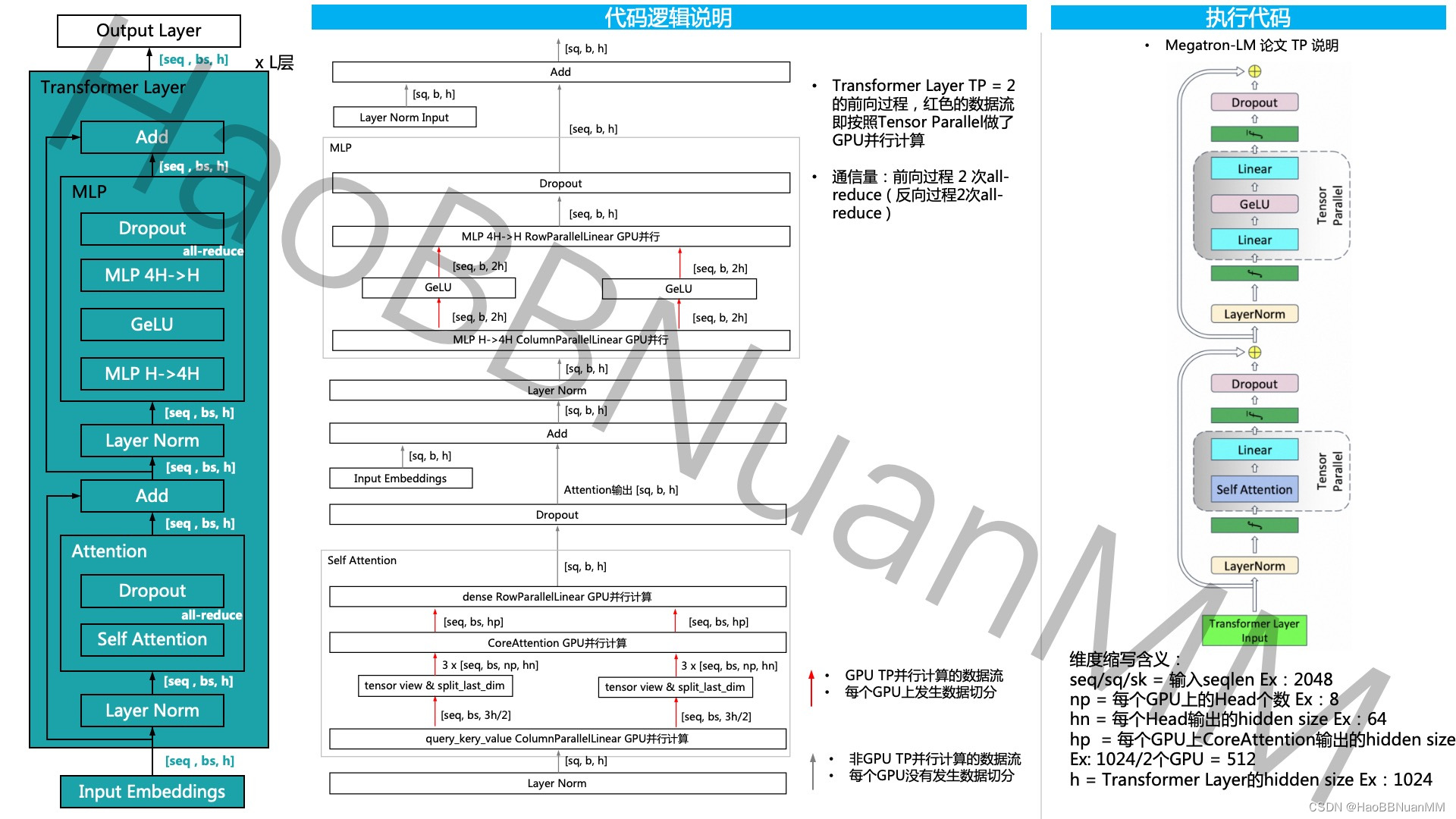
Megatron-LM GPT 源码分析(一) Tensor Parallel分析
引言 本文基于开源代码 GitHub - NVIDIA/Megatron-LM: Ongoing research training transformer models at scale ,通过GPT的模型运行示例,从三个维度 - 模型结构、代码运行、代码逻辑说明 对其源码做深入的分析。 Tensor Parallel源码分析...

分类预测 | MATLAB实现SSA-CNN-GRU麻雀算法优化卷积门控循环单元数据分类预测
分类预测 | MATLAB实现SSA-CNN-GRU麻雀算法优化卷积门控循环单元数据分类预测 目录 分类预测 | MATLAB实现SSA-CNN-GRU麻雀算法优化卷积门控循环单元数据分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.MATLAB实现SSA-CNN-GRU麻雀算法优化卷积门控循环单元数据…...

婚礼的魅力
昨日有幸被邀请去当伴郎,虽然是替补,即别人鸽了,过去救急,但总归是去起作用。 婚礼的魅力,感受到了,满满的仪式感,紧凑的流程,还有不断的拍照,做视频,留下美好…...
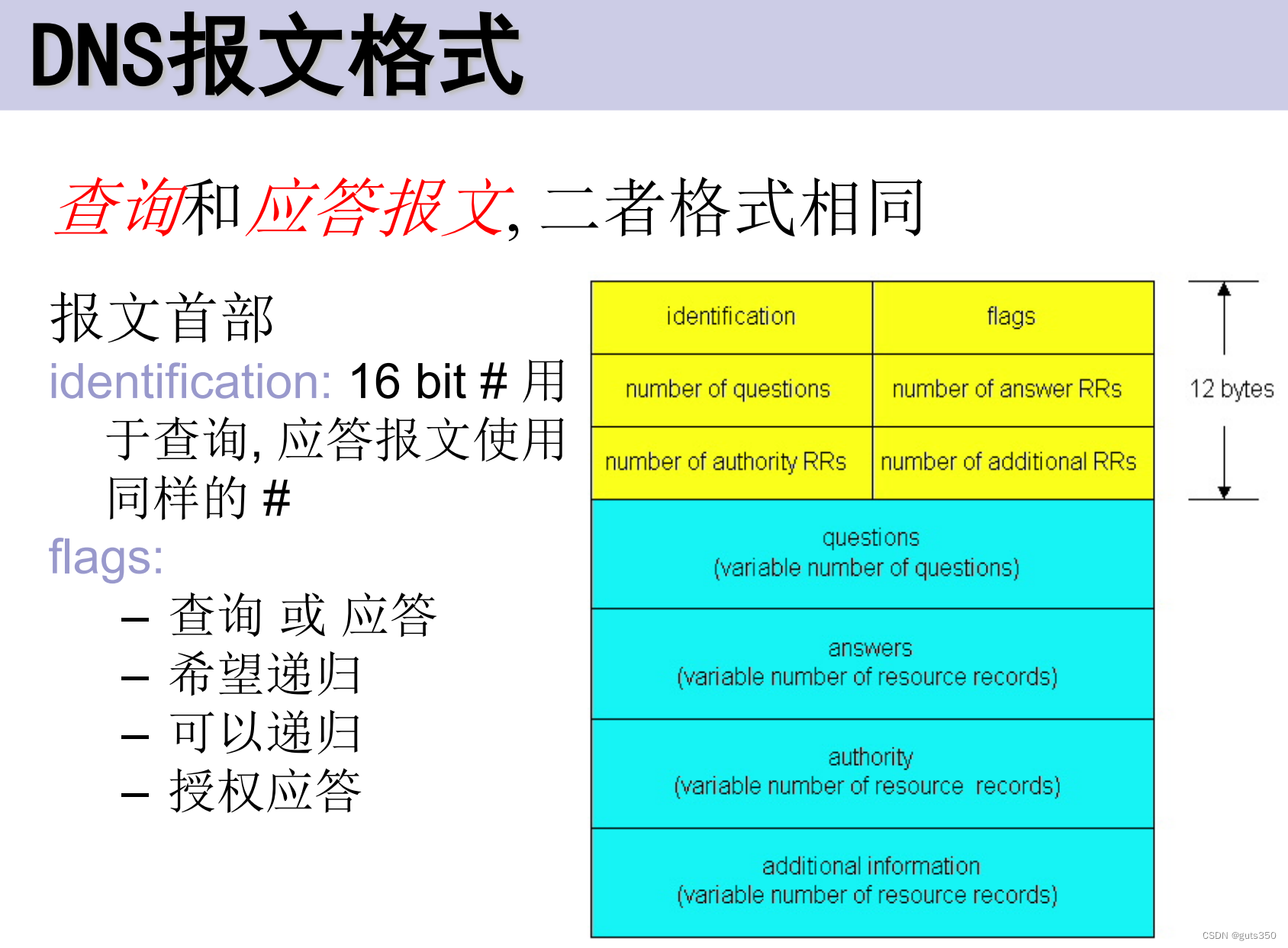
【计算机网络笔记】DNS报文格式
DNS 提供域名到主机IP地址的映射 域名服务的三大要素: 域(Domain)和域名(Domain name): 域指由地 理位置或业务类型而联系在一起的一组计算机构 成。 主机:由域名来标识。域名是由字符和(或&a…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
