红黑树
红黑树是一个相对的平衡,减少了旋转的消耗
- 一个节点不是红的就是黑的
- 根节点是黑的
- 一个节点是红的,孩子是黑的(没有连续的红色节点)
- 对于每个节点,从该节点到后代节点的简单路径,都包含相同的黑色(黑色节点的数量相等)
- 每个叶子节点都是黑色的(null节点)
最长路径不超过最短路劲的2倍
最短路径:全黑
最长路径: 一黑一红
假设每条路径黑节点是N,
n<=random path<=2n
路径要数到空位置
左右两边没那么均衡:整体的高度
假设红黑树中一中路径黑色节点=x
高度2x>=h>=x
全黑 一黑一红
2x-1<=N<=22x-1:N为节点个数
X>=logx(N),x<=log(N)/2
添加节点
添加节点主要是添加红色节点
以父亲为祖父的左节点为例
- 叔叔存在且为红色
把父亲和叔叔都改成黑色
把祖父改成红色 - 叔叔不存在或为黑色
- 我为父亲的左节点,进行一个右单旋,并把父亲改成黑色,把祖父改成红色
- 我为父亲的右节点,进行一个左右双旋,把我改黑,祖父改红
父亲为祖父的右节点与之相反
#pragma once
#include <iostream>
using namespace std;enum Color
{RED,BLACK
};
template <class K, class V>struct RBTreeNode
{RBTreeNode *_left;RBTreeNode *_right;RBTreeNode *_parent;pair<K, V> _kv;Color _col; //控制颜色RBTreeNode(const pair<K, V> &kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED)//一开始的颜色给红色{}
};template <class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;private:Node *_root;private:void _InOrder(Node *root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateR(Node *parent){//右单旋转Node *subL = parent->_left; //子节点Node *subLR = subL->_right; //子节点的右节点Node *parentparent = parent->_parent; //出问题节点的父节点parent->_left = subLR;subL->_right = parent;parent->_parent = subL;if (subLR)subLR->_parent = parent;//和父节点的父节点连接if (parent == _root){//要旋转的节点已经是根//更新根_root = subL;_root->_parent = nullptr; //更新顶部}else{//父节点上面还有节点if (parentparent->_left == parent){//是左节点subL->_parent = parentparent;parentparent->_left = subL;}else{subL->_parent = parentparent;parentparent->_right = subL;}}}void RotateL(Node *parent) //左单旋{Node *subR = parent->_right;Node *subRL = subR->_left;Node *parentparent = parent->_parent;parent->_parent = subR;subR->_left = parent;parent->_right = subRL;if (subRL)subRL->_parent = parent;if (parent == _root){_root = subR;_root->_parent = nullptr;}else{if (parentparent->_right == parent){parentparent->_right = subR;subR->_parent = parentparent;}else{parentparent->_left = subR;subR->_parent = parentparent;}}}public:RBTree(): _root(nullptr){}bool Insert(const pair<K, V> &kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//Node *cur = _root;Node *parent = nullptr; //还要找到父亲while (cur){if (cur->_kv.first > kv.first) //比它小,在左边{parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first) //比他大,在右边{parent = cur;cur = cur->_right;}else{return false;}}//走到这里,就可以链接上cur = new Node(kv);cur->_col = RED; //新增节点颜色给红色cur->_parent = parent; //链接上父亲if (parent->_kv.first > kv.first){//比他小,在左边parent->_left = cur;}else{parent->_right = cur;}//插入之前一定是红黑树//这里就要控制平衡,通过颜色//插入黑节点(影响路径),还是红节点(只影响自己的,不影响其他区域)//往上调整//我为红,父亲如果为红,爷爷一定是黑色// 1.叔叔存在且为红while (parent && parent->_col == RED) //往上处理,父亲颜色为红色,就要处理,黑色就不要处理,为红,就不是根{Node *grandparent = parent->_parent;if (parent == grandparent->_left){Node *uncle = grandparent->_right; //叔叔就是在右边//叔叔存在且为红if (uncle && uncle->_col == RED){//叔叔存在,且为红//变色,继续向上处理parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent; //继续迭代往上操作parent = cur->_parent;}//叔叔不存在else //不存在,或存在且为黑{//不存在,进行旋转//旋转+变色if (cur == parent->_left){RotateR(grandparent); //进行右单旋转//变色parent->_col = BLACK;grandparent->_col = RED;}else{//双旋//左右双旋// p进行右单旋,g左单旋,g变红藕,cur变黑,RotateL(parent);RotateR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}else //父亲是祖父的右边{Node *uncle = grandparent->_left; //叔叔就是在右边//叔叔存在且为红if (uncle && uncle->_col == RED){//叔叔存在,且为红//变色,继续向上处理parent->_col = BLACK;uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent; //继续迭代往上操作parent = cur->_parent;}//叔叔不存在else //不存在,或存在且为黑{//不存在,进行旋转//旋转+变色if (cur == parent->_right){RotateL(grandparent); //进行右单旋转//变色parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}_root->_col = BLACK; //根的一定是黑色return true;}bool IsBalance(){if(_root&&_root->_col==RED){cout<<"根节点是黑色"<<endl;return false;}int basevalue=0;//基准值Node* left=_root;while(left){if(left->_col==BLACK){basevalue++;}left=left->_left;}//用最左路径黑色节点的数量,做基准值int blacknum=0;//每个节点的黑色个数return _IsBalance(_root,basevalue,blacknum);}void InOrder() //不能验证是不是AVL树{_InOrder(_root);}private:bool _IsBalance(Node* root,int basevalue,int blacknum){//根节点是黑的//红色,孩子是黑色,没有连续的红节点//每个路径含有相同的黑色if(root==nullptr){//一条路径走完了if(basevalue!=blacknum){//每条路劲都有blacknumcout<<"存在黑色节点数量不相等"<<endl;return false;}return true;}if(root->_col==RED&&root->_parent->_col==RED)//红节点{//检查它的父亲,一定有 cout<<"出现连续的红节点"<<endl;return false;}if(root->_col==BLACK){blacknum++;}return _IsBalance(root->_left,basevalue,blacknum)&&_IsBalance(root->_right,basevalue,blacknum);//没有用引用,下面的加加,不会影响下面}
};void test()
{RBTree<int, int> rbt;int a[]={16,3,7,11,9,26,18,14,15};// int a[] = {4,2,6,1,3,5,15,7,16,14};for (auto e : a){rbt.Insert(make_pair(e, e));}cout<<rbt.IsBalance()<<endl;rbt.InOrder();
}
相关文章:

红黑树
红黑树是一个相对的平衡,减少了旋转的消耗 一个节点不是红的就是黑的根节点是黑的一个节点是红的,孩子是黑的(没有连续的红色节点)对于每个节点,从该节点到后代节点的简单路径,都包含相同的黑色࿰…...
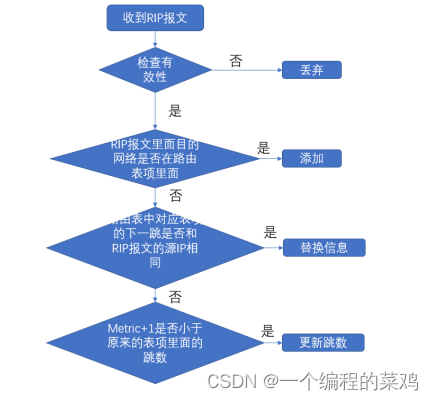
RIP路由协议的更新(电子科技大学TCP/IP第二次实验)
一.实验目的 1、掌握 RIP 协议在路由更新时的发送信息和发送方式 2、掌握 RIP 协议的路由更新算法 二.预备知识 1、静态路由选择和动态路由选择 2、内部网关协议和外部网关协议 3、距离向量路由选择 三.实验原理 RIP 协议(…...

基于JWT实现用户身份认证
常见场景 账号/密码登录、手机号验证码登录、微信扫码登录 解决方案 基于Session认证方案 什么是session认证方案 服务端生成httpsession认证(内存-sessionId)sessionId写到浏览器cookie浏览器请求的header中自动带sessionId到服务端服务端校验sessionId是否合法 优点 .…...
)
SaltStack 远程命令执行漏洞(CVE-2020-16846)
目录 (一)漏洞描述 (二)漏洞复现 1、在vulhub上启动docker 2、访问docker靶机 https /ip:8000...

SAP 详细解析成本收集器
成本收集器作为成本对象,主要应用于按期间进行成本核算的情况,在这种情况下会把产品创建为成本收集器,实际成本的收集和差异的结算全部按照成本收集器进行处理,财务的成本分析也针对成本收集器进行。 成本收集器是按期间核算&am…...

Vision Transformer学习了什么-WHAT DO VISION TRANSFORMERS LEARN? A VISUAL EXPLORATION
WHAT DO VISION TRANSFORMERS LEARN? A VISUAL EXPLORATION 文章地址 代码地址 摘要 视觉转换器( Vision Transformers,ViTs )正在迅速成为计算机视觉的事实上的架构,但我们对它们为什么工作和学习什么知之甚少。虽然现有研究对卷积神经网络的机制进…...

一种全新的图像滤波理论的实验(三)
一、前言 2023年02月22日,我发布了滤波后,为针对异常的白色和黑色像素进行处理的实验,本次发布基于上下文处理的方案的实验,目的是通过基于加权概率模型滤波后,在逆滤波时直接修复大量的白色和黑色的异常像素…...
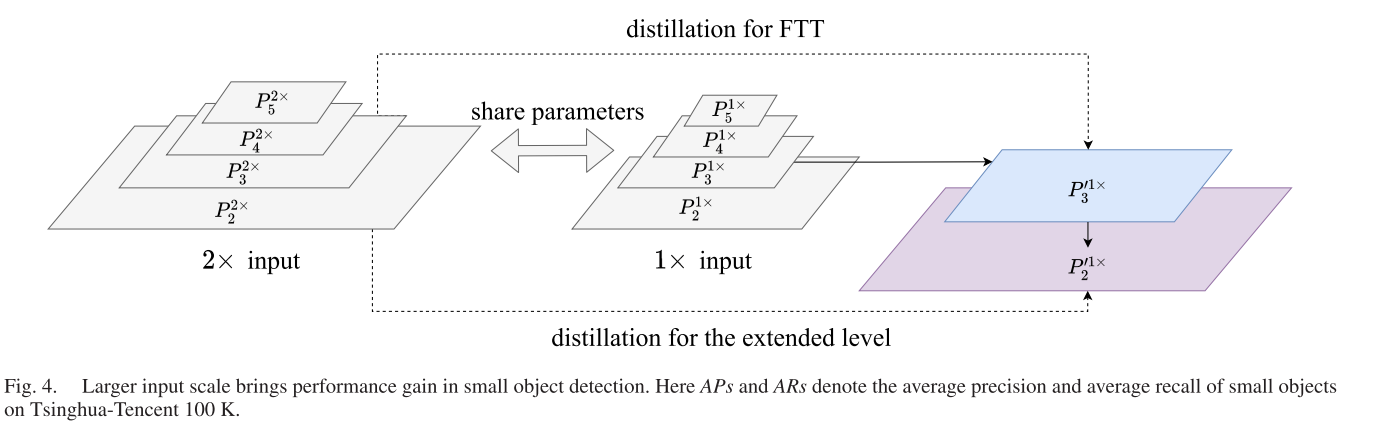
CV——day79 读论文:基于小目标检测的扩展特征金字塔网络
Extended Feature Pyramid Network for Small Object DetectionI. INTRODUCTIONII. RELATED WORKA. 深层物体探测器B. 跨尺度特征C. 目标检测中的超分辨率III. OUR APPROACHA. 扩展特征金字塔网络B. 特征纹理传输C. 交叉分辨蒸馏IV. EXPERIMENTSA. Experimental Settings1&…...
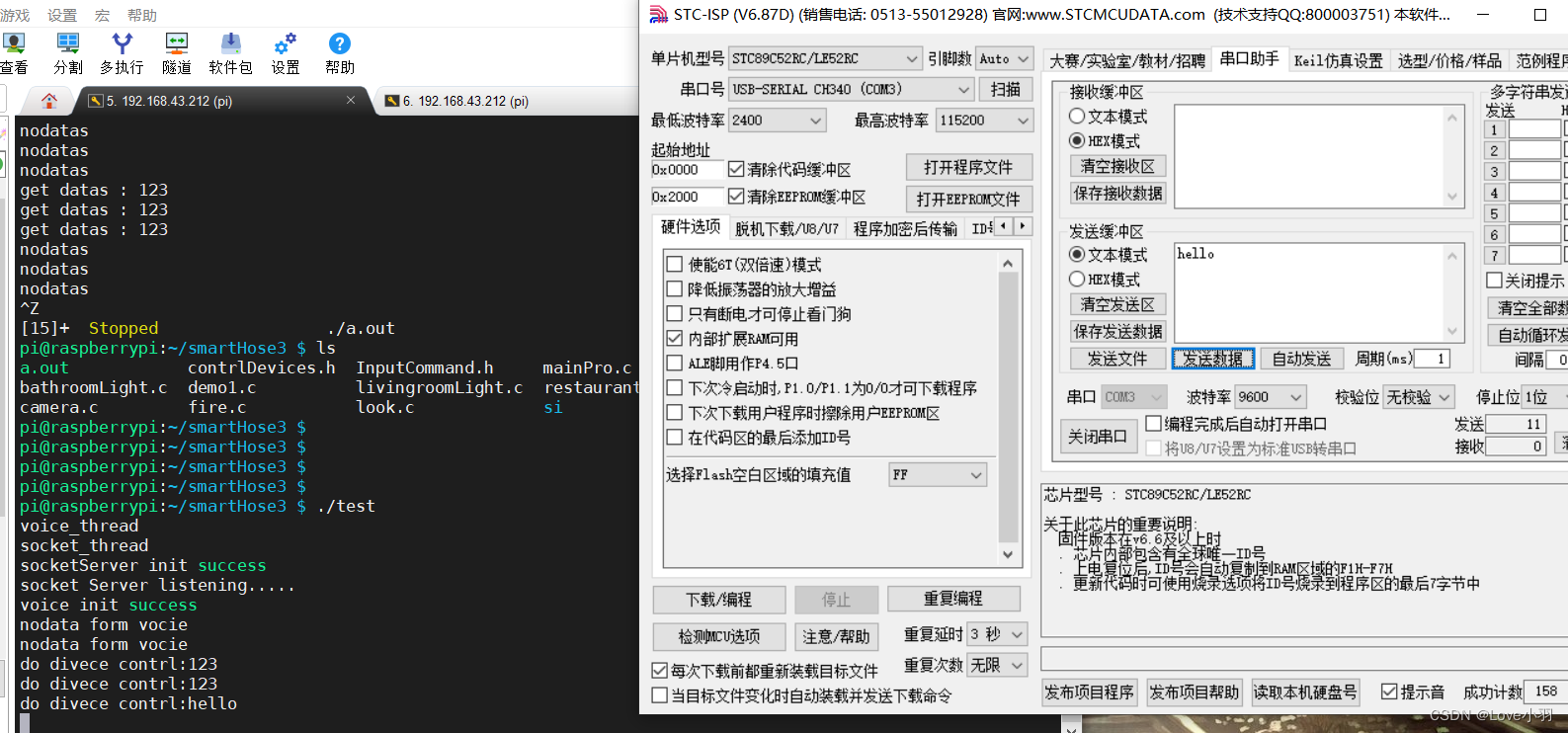
智能家居项目(五)测试串口功能
目录 一、写一个单独测试串口的demo 二、直接运行上一篇智能家居的代码 一、写一个单独测试串口的demo 1、TTL串口与树莓派的连接方式 (1)TTL的RXD和TXD针脚连接到树莓的TXD和RXD上(T–>R R–>T),交叉连&…...

2023年全国最新道路运输从业人员精选真题及答案7
百分百题库提供道路运输安全员考试试题、道路运输从业人员考试预测题、道路安全员考试真题、道路运输从业人员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 71.根据《中华人民共和国安全生产法》,生产经营单位…...

python的所有知识点(含讲解),不看就亏死了
目录 简介 特点 搭建开发环境 版本 hello world 注释 文件类型 变量 常量 数据类型 运算符和表达式 控制语句 数组相关 函数相关 字符串相关 文件处理 对象和类,注:不是那个对象!!!!&…...

【Servlet篇】Response对象详细解读
文章目录Response 继承体系Response 设置响应数据设置响应行数据设置响应头数据设置响应体数据Response 重定向Response 响应字符数据Response 响应字节数据Response 继承体系 前面说到,我们使用 Request 对象来获取请求数据,使用 Response 对象来设置响…...

SAP FICO期初开账存货导入尾差
一、问题 1.AFS物料网格级别库存导入先除再乘有尾差: 旧系统数据迁移自两个系统:一个管理数量账(网格级别),一个管理金额账(物料级别) 2.MB52分工厂与MB5L分工厂统计差异: M…...
微信商城小程序怎么做_分享实体店做微信商城小程序制作步骤
各行各业都在用微商城小程序开店,不管是餐饮店还是便利店,还是五金店。都是可以利用微信小程序开一个线上店铺。实现线上跟线下店铺更加全面的结合。维护好自己的老客户。让您的客户给您拉新,带来新客户。小程序经过这几年的快速发展和不断升…...

【moment.js】时间格式化插件
Moment.js 用于在JavaScript中解析,验证,操作和显示日期和时间。是一款在项目中使用频率极高的时间格式化工具,Ant Design Vue 组件中就是使用它来处理时间的。 安装 npm install moment --save # npm yarn add moment # Ya…...

微信小程序开发【壹】
随手拍拍💁♂️📷 日期: 2023.02.24 地点: 杭州 介绍: 2023.02.24上午十点,路过学院的教学楼时🏢,突然看见了一团粉红色。走进一看是一排梅花🌸,赶在它们凋零前,将它们定格在我的相…...

2 k-近邻算法
0 问题引入 想一想:下面图片中有三种豆,其中三颗豆品种未知,如何判断他们类型? 1 KNN概述 1.1 KNN场景 电影可以按照题材分类,那么如何区分 动作片 和 爱情片 呢? 动作片:打斗次数更多爱情…...
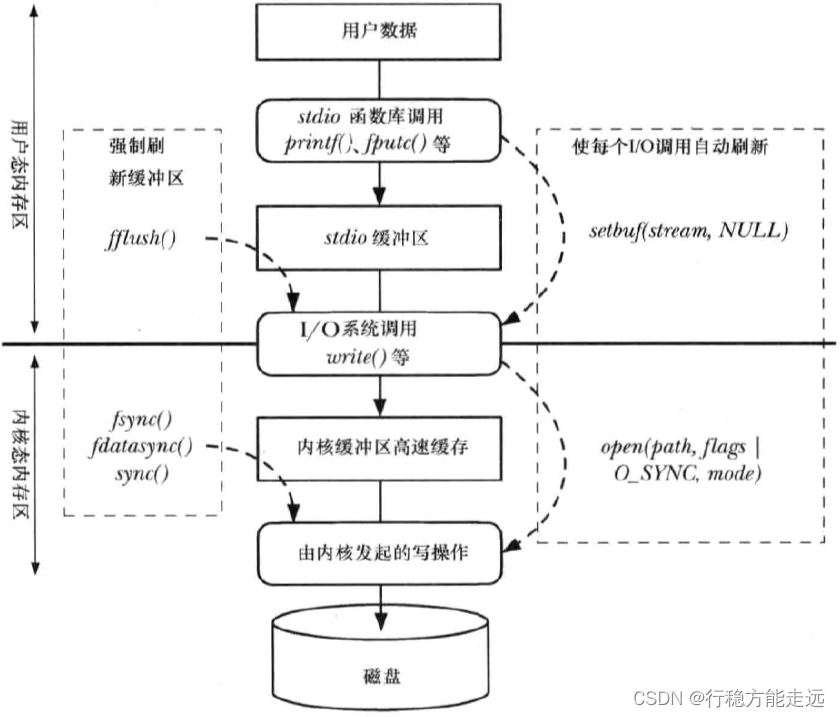
深入探究文件I/O
目录Linux 系统如何管理文件静态文件与inode文件打开时的状态返回错误处理与errnostrerror 函数perror 函数exit、_exit、_Exit_exit()和_Exit()函数exit()函数空洞文件概念实验测试O_APPEND 和O_TRUNC 标志O_TRUNC 标志O_APPEND 标志多次打开同一个文件验证一些现象多次打开同…...
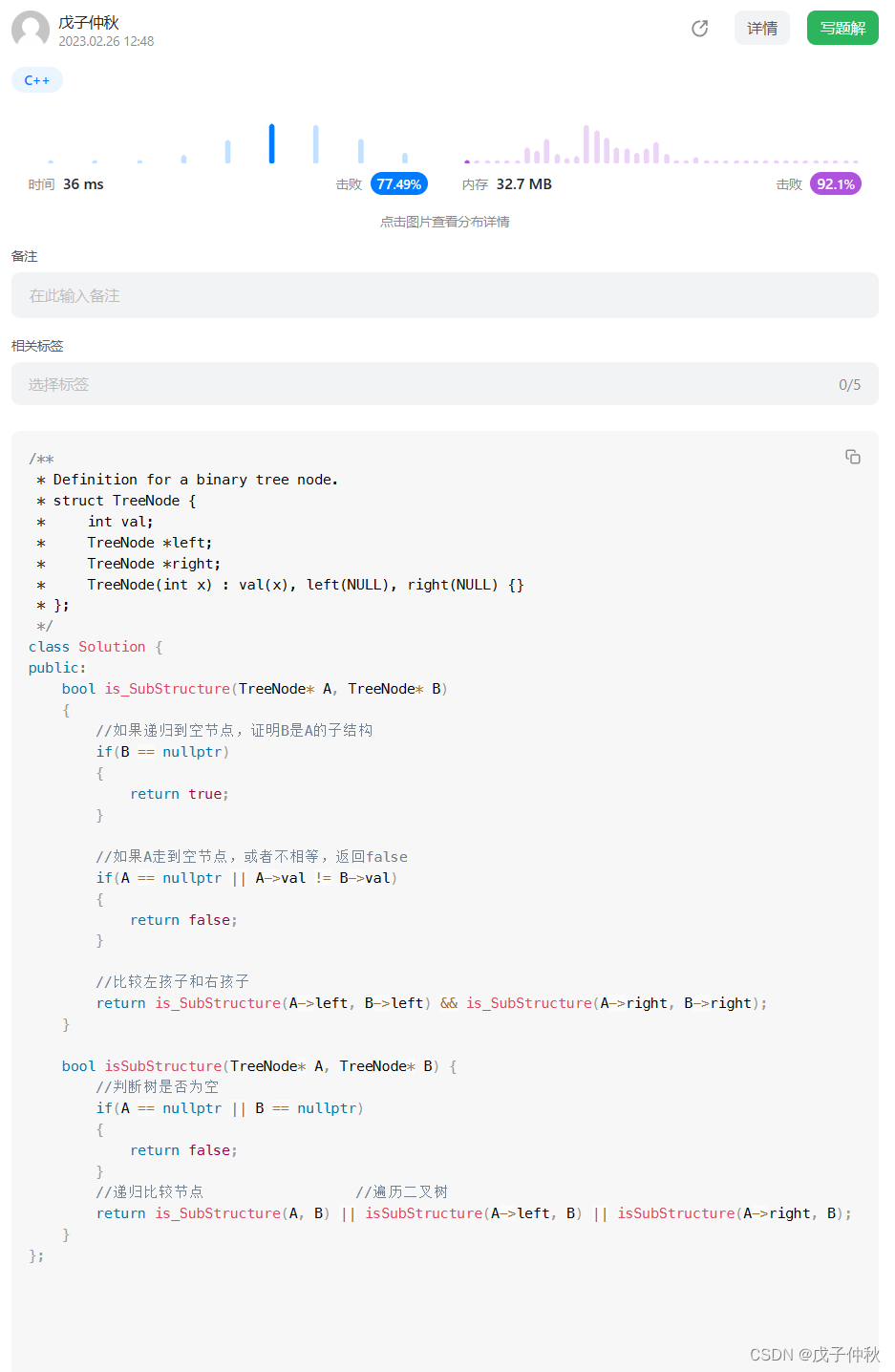
【LeetCode】剑指 Offer(9)
目录 题目:剑指 Offer 25. 合并两个排序的链表 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 26. 树的子结构 - 力扣&#…...

python 遍历可迭代对象的方法
python 遍历可迭代对象的方法 可迭代(iterable) 迭代(遍历)就是按照某种顺序逐个访问对象中的每一项。 Python中有很多对象都是可以通过for语句来直接遍历的,例如list、string、dict等,这些对象都是可迭代的,被称为可迭代对象。 可以将可迭…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
