LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
我们构建了一个包含 n 行( 索引从 1 开始 )的表。首先在第一行我们写上一个 0。接下来的每一行,将前一行中的0替换为01,1替换为10。
- 例如,对于
n = 3,第1行是0,第2行是01,第3行是0110。
给定行数 n 和序数 k,返回第 n 行中第 k 个字符。( k 从索引 1 开始)
示例 1:
输入: n = 1, k = 1
输出: 0
解释: 第一行:0
示例 2:
输入: n = 2, k = 1
输出: 0
解释:
第一行: 0
第二行: 01
示例 3:
输入: n = 2, k = 2
输出: 1
解释:
第一行: 0
第二行: 01
提示:
1 <= n <= 301 <= k <= 2^n - 1
解法 递归
首先题目给出一个 n n n 行的表(索引从 1 1 1 开始)。并给出表的构造规则为:第一行仅有一个 0 0 0,然后接下来的每一行可以由上一行中 0 0 0 替换为 01 01 01, 1 1 1 替换为 10 10 10 来生成。
- 比如当 n = 3 n = 3 n=3 时,第 1 1 1 行是 0 0 0,第 2 2 2 行是 01 01 01,第 3 3 3 行是 0110 0110 0110 。
现在要求表第 n n n 行中第 k k k 个数字, 1 ≤ k ≤ 2 n 1 \le k \le 2 ^ n 1≤k≤2n 。首先我们可以看到第 i i i 行中会有 2 i − 1 2^{i-1} 2i−1 个数字, 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n ,且其中第 j j j 个数字按照构造规则会生第 i + 1 i + 1 i+1 行中的第 2 ∗ j − 1 2*j - 1 2∗j−1 和 2 ∗ j 2∗j 2∗j 个数字, 1 ≤ j ≤ 2 i − 1 1 \le j \le 2^{i-1} 1≤j≤2i−1 。
即对于第 i + 1 i + 1 i+1 行中的第 x x x 个数字 num 1 \textit{num}_1 num1 , 1 ≤ x ≤ 2 i 1 \le x \le 2^i 1≤x≤2i ,会被第 i i i 行中第 ⌊ x + 1 2 ⌋ \lfloor \frac{x + 1}{2} \rfloor ⌊2x+1⌋ 个数字 num 2 \textit{num}_2 num2 生成。且满足规则:
- 当 num 2 = 0 \textit{num}_2 = 0 num2=0 时, num 2 \textit{num}_2 num2 会生成 01 01 01:
num 1 = { 0 , x ≡ 1 ( m o d 2 ) 1 , x ≡ 0 ( m o d 2 ) \textit{num}_1 = \begin{cases} 0, & x \equiv 1 \pmod{2} \\ 1, & x \equiv 0 \pmod{2} \\ \end{cases} num1={0,1,x≡1(mod2)x≡0(mod2) - 当 n u m 2 = 1 num_2 = 1 num2=1 时, num 2 \textit{num}_2 num2 会生成 10 10 10:
num 1 = { 1 , x ≡ 1 ( m o d 2 ) 0 , x ≡ 0 ( m o d 2 ) \textit{num}_1 = \begin{cases} 1, & x \equiv 1 \pmod{2} \\ 0, & x \equiv 0 \pmod{2} \\ \end{cases} num1={1,0,x≡1(mod2)x≡0(mod2)
并且进一步总结我们可以得到: num 1 = ( x & 1 ) ⊕ 1 ⊕ num 2 \textit{num}_1 = (x \And 1) \oplus 1 \oplus \textit{num}_2 num1=(x&1)⊕1⊕num2 ,其中 & \And & 为「与」运算符, ⊕ \oplus ⊕ 为「异或」运算符。那么我们从第 n n n 不断往上递归求解,并且当在第一行时只有一个数字,直接返回 0 0 0 即可。
class Solution {
public:int kthGrammar(int n, int k) {if (n == 1) return 0;return (k & 1) ^ 1 ^ kthGrammar(n - 1, (k + 1) / 2);}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数,递归深度为 n n n。
- 空间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数,主要为递归的空间开销。
解法2 找规律 + 递归
按照方法一,我们可以尝试写表中的前几行:
- 0 0 0
- 01 01 01
- 0110 0110 0110
- 01101001 0110 1001 01101001
- ⋯ \cdots ⋯
我们可以注意到规律:每一行的后半部分正好为前半部分的“翻转”——前半部分是 0 0 0 后半部分变为 1 1 1,前半部分是 1 1 1,后半部分变为 0 0 0。且每一行的前半部分和上一行相同。我们可以通过「数学归纳法」来进行证明。
有了这个性质,那么我们再次思考原问题:对于查询某一个行第 k k k 个数字,如果 k k k 在后半部分,那么原问题就可以转化为求解该行前半部分的对应位置的“翻转”数字,又因为该行前半部分与上一行相同,所以又转化为上一行对应对应的“翻转”数字。那么按照这样一直递归下去,并在第一行时返回数字 0 0 0 即可。
class Solution {
public:int kthGrammar(int n, int k) {if (k == 1) return 0;// 查询某一个行第k数,如果k在后半部分,可转化为求解该行前半部分对应位置的翻转数字if (k > (1 << (n - 2))) return 1 ^ kthGrammar(n - 1, k - (1 << (n - 2)));return kthGrammar(n - 1, k); // 一行前半部分和上一行相同}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数。
- 空间复杂度: O ( n ) O(n) O(n),其中 n n n 为题目给定表的行数,主要为递归的空间开销。
解法3 找规律 + 位运算
在「方法二」的基础上,我们来进行优化,本质上我们其实只需要求在过程中的“翻转”总次数,如果“翻转”为偶数次则原问题求解为 0 0 0 ,否则为 1 1 1。
首先我们修改行列的索引从 0 0 0 开始,此时原先第 p p p 行的索引现在为 p − 1 p - 1 p−1 行,第 i i i 行有 2 i 2 ^ i 2i 位。那么对于某一行 i i i 中下标为 x x x 的数字,如果 x < 2 i − 1 x < 2^{i - 1} x<2i−1 那么等价于求 i − 1 i - 1 i−1 行中下标为 x x x 的数字,否则 x x x 的二进制位的从右往左第 i i i 位(从第 0 0 0 位开始)为 1 1 1 ,此时需要减去该位(“翻转”一次),然后递归求解即可。所以我们可以看到最后“翻转”的总次数只和初始状态下的下标 x x x 二进制表示中 1 1 1 的个数有关。
因此原问题中求“翻转”的总次数,就等价于求 k − 1 k - 1 k−1 的二进制表示中 1 1 1 的个数。
class Solution {
public:int kthGrammar(int n, int k) {// return __builtin_popcount(k - 1) & 1;k--;int res = 0;while (k > 0) {k &= k - 1;res ^= 1;}return res;}
};
复杂度分析:
- 时间复杂度: O ( log k ) O(\log k) O(logk) ,其中 k k k 为题目给定查询的下标。
- 空间复杂度: O ( 1 ) O(1) O(1) ,仅使用常量变量。
相关文章:

LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
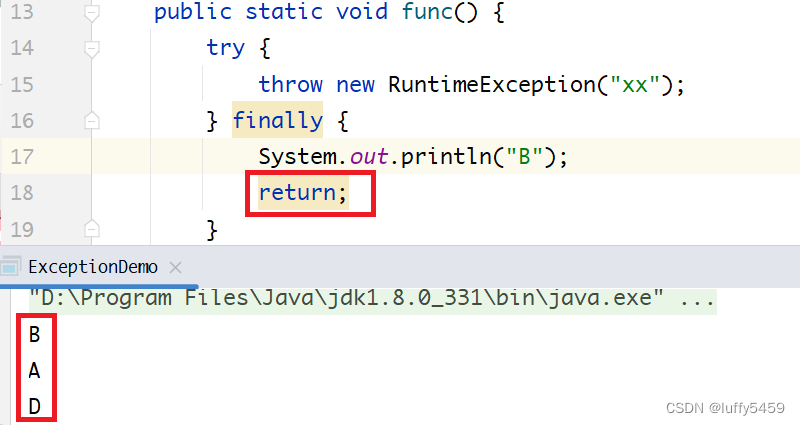
java try throw exception finally 遇上 return break continue造成异常丢失
如下所示,是一个java笔试题,考察的是抛出异常之后,程序运行结果,但是这里抛出异常,并没有捕获异常,而是通过finally来进行了流程控制处理。 package com.xxx.test;public class ExceptionFlow {public sta…...
+ Spring相关源码)
设计模式——装饰器模式(Decorator Pattern)+ Spring相关源码
文章目录 一、装饰器模式的定义二、个人理解举个抽象的例(可能并不是很贴切) 三、例子1、菜鸟教程例子1.1、定义对象1.2、定义装饰器 3、JDK源码 ——包装类4、JDK源码 —— IO、OutputStreamWriter5、Spring源码 —— BeanWrapperImpl5、SpringMVC源码 …...
MATLAB R2018b详细安装教程(附资源)
云盘链接: pan.baidu.com/s/1SsfNtlG96umfXdhaEOPT1g 提取码:1024 大小:11.77GB 安装环境:Win10/Win8/Win7 安装步骤: 1.鼠标右击【R2018b(64bit)】压缩包选择【解压到 R2018b(64bit)】 2.打开解压后的文件夹中的…...
GEE错误——影像加载过程中出现的图层无法展示的解决方案
问题: // I dont know if some standard value exists for the radius, in the same, I will assume that some software would prefer to use square shape, but circle makes more sense to me. // pixels is noice if you want to zoom in and out to visualize…...
读图数据库实战笔记03_遍历
1. Gremlin Server只将数据存储在内存中 1.1. 如果停止Gremlin Server,将丢失数据库里的所有数据 2. 概念 2.1. 遍历(动词) 2.1.1. 当在图数据库中导航时,从顶点到边或从边到顶点的移动过程 2.1.2. 类似于在关系数据库中的查…...

QT如何检测当前系统是是Windows还是Uninx或Mac?以及是哪个版本?
简介 通过Qt获取当前系统及版本号,需要用到QSysInfo。 QSysInfo类提供有关系统的信息。 WordSize指定了应用程序编译所在的平台的指针大小。 ByteOrder指定了平台是大端序还是小端序。 某些常量仅在特定的平台上定义。您可以使用预处理器符号Q_OS_WIN和Q_OS_MACOS来…...
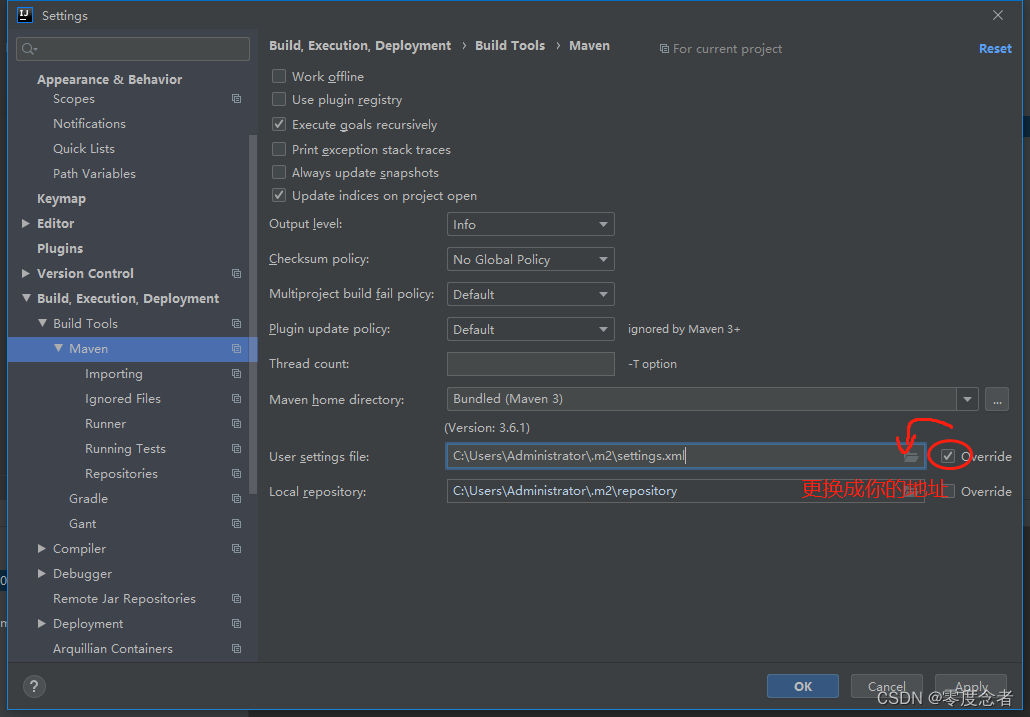
Maven配置阿里云中央仓库settings.xml
Maven配置阿里云settings.xml 前言一、阿里云settings.xml二、使用步骤1.任意目录创建settings.xml2.使用阿里云仓库 总结 前言 国内网络从maven中央仓库下载文件通常是比较慢的,所以建议配置阿里云代理镜像以提高jar包下载速度,IDEA中我们需要配置自己…...

由浅入深C系列八:如何高效使用和处理Json格式的数据
如何高效使用和处理JSON格式的数据 问题引入关于CJSON示例代码头文件引用处理数据 问题引入 最近的项目在用c处理后台的数据时,因为好多外部接口都在使用Json格式作为返回的数据结构和数据描述,如何在c中高效使用和处理Json格式的数据就成为了必须要解决…...
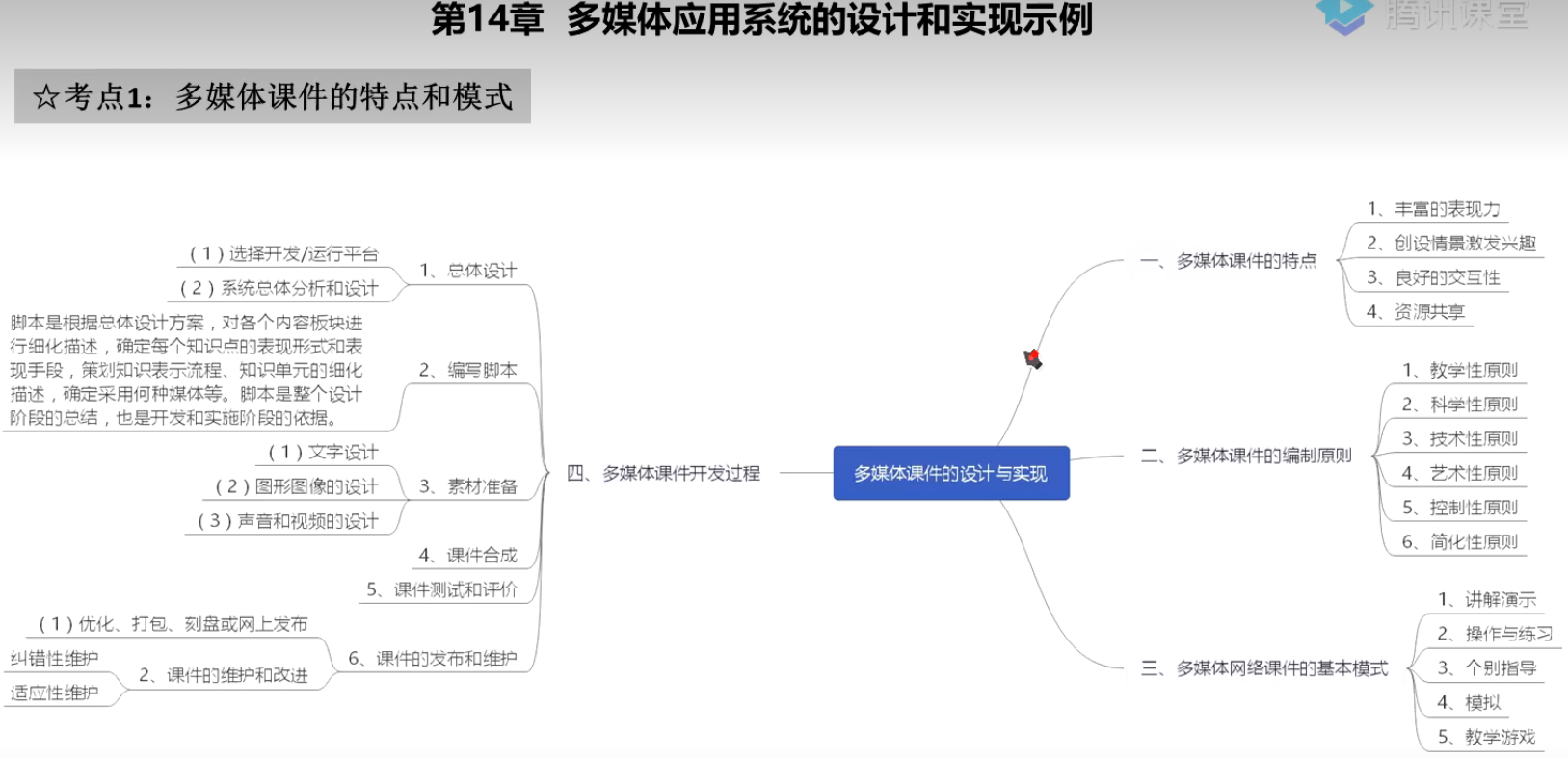
多媒体应用设计师 第16章 多媒体应用系统的设计和实现示例
口诀 思维导图 2020...

golang平滑重启库overseer实现原理
overseer主要完成了三部分功能: 1、连接的无损关闭,2、连接的平滑重启,3、文件变更的自动重启。 下面依次讲一下: 一、连接的无损关闭 golang官方的net包是不支持连接的无损关闭的,当主监听协程退出时,…...
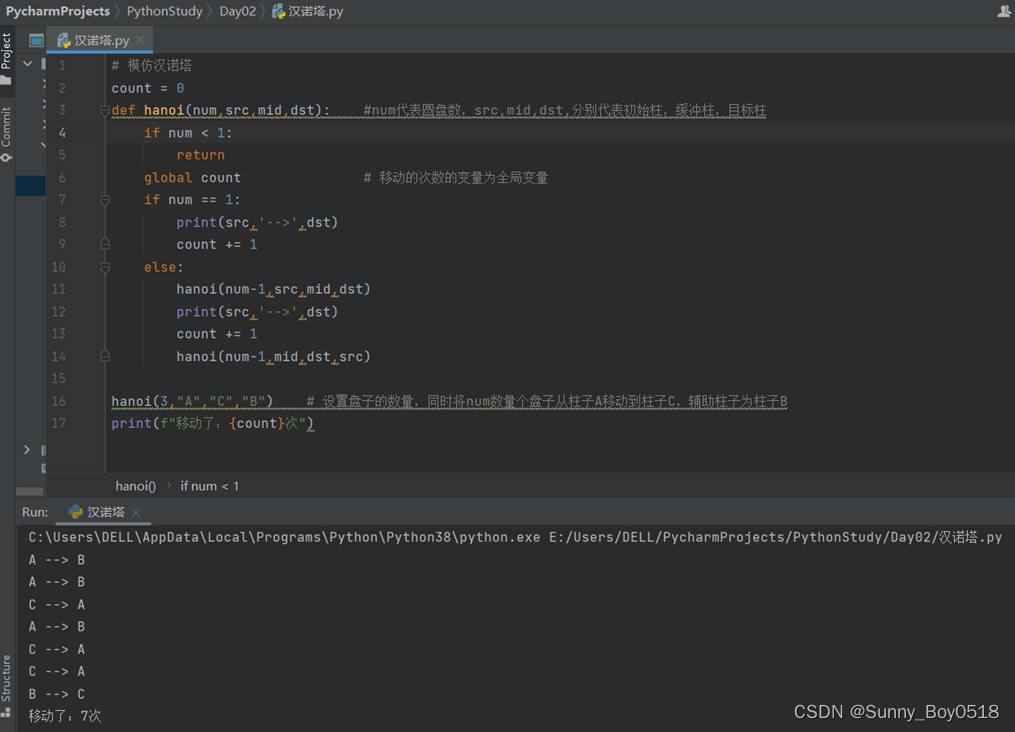
用Python定义一个函数,用递归的方式模拟汉诺塔问题
【任务需求】 定义一个函数,用递归的方式模拟汉诺塔问题,三个柱子,分别为A、B、C,其中A柱子上有N个盘子,从小到大编号为1到N,盘子大小不同。现在要将这N个盘子从A柱子移动到C柱子上,但移动的过…...

二手的需求
案例1030 某天项目经理小王,从用户现场带回了需求,以图形的方式,交给了产品经理。告诉他就照这样设计,结果是项目经理放弃让产品经理出效果图。 原因是产品经理觉得项目经理带回来的需求有问题。项目经理解释产品经理不接受&…...
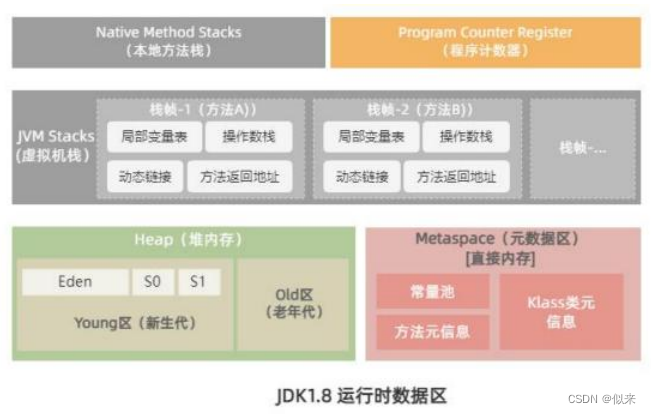
大厂面试题-JVM为什么使用元空间替换了永久代?
目录 面试解析 问题答案 面试解析 我们都知道Java8以及以后的版本中,JVM运行时数据区的结构都在慢慢调整和优化。但实际上这些变化,对于业务开发的小伙伴来说,没有任何影响。 因此我可以说,99%的人都回答不出这个问题。 但是…...
基本微信小程序的驾校宝典系统-驾照考试系统
项目介绍 系统模块分析是对系统的各个模块做出相应的说明以及解释。此系统的模块分别有用户模块、服务端模块和管理端模块这两大基本模块,其中服务端模块包括了首页、教练信息、教练咨讯、考试预约、我的等;而管理端模块则包括了个人中心、用户管理、教…...
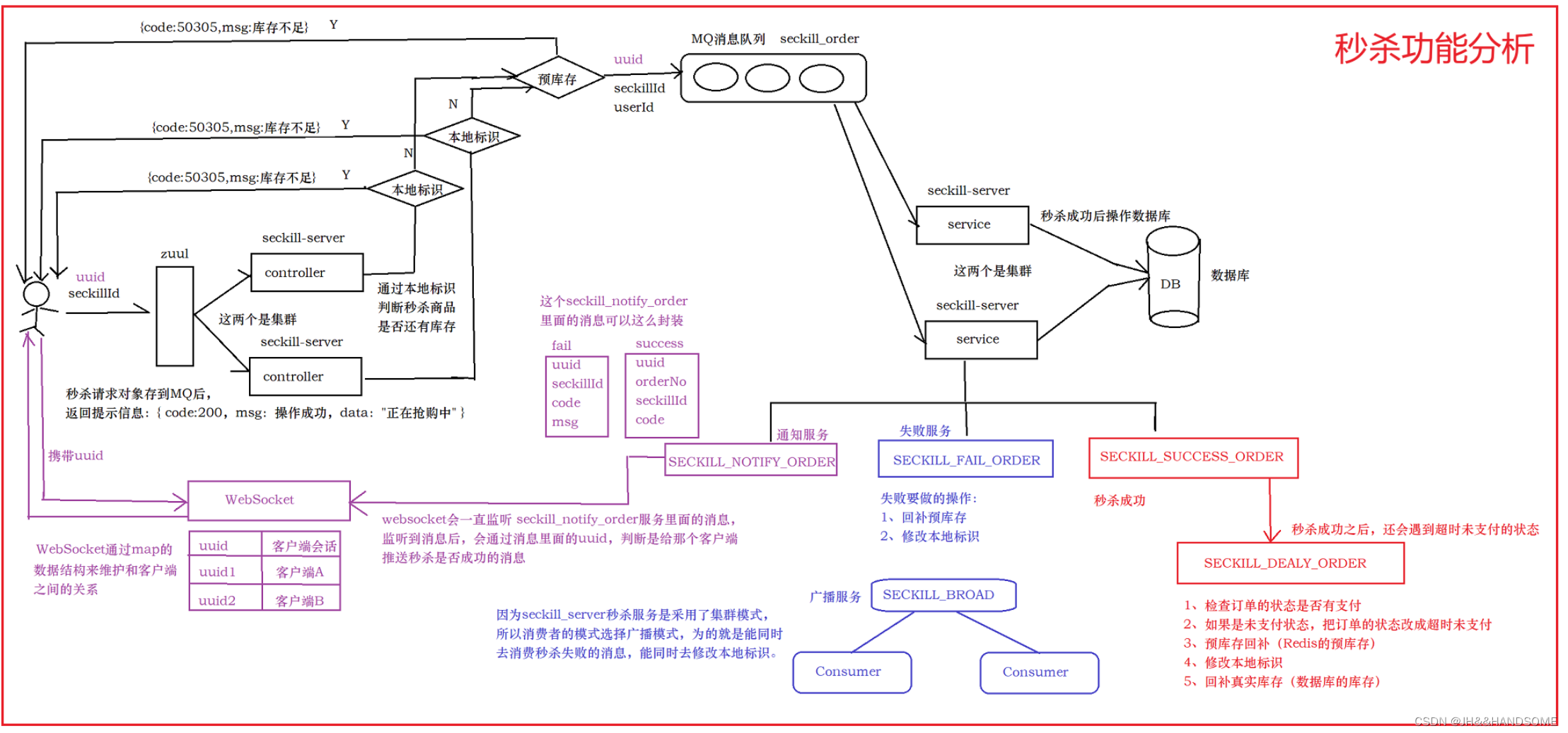
02、SpringCloud -- Redis和Cookie过期时间刷新功能
目录 需求:代码流程过滤器类工具类过滤判断远程调用feign接口gitee 配置接口实现过滤器run方法测试:问题:秒杀功能完整分析图 需求: cookie应该写在网关中,网关中可以自定义filter过滤器,用来实现cookie的刷新和redis中key的刷新,延长用户的操作时间。 就是让用户每操…...

【报错】kali安装ngrok报错解决办法(zsh: exec format error: ./ngrok)
问题描述 kali安装ngrok令牌授权失败 在安装配置文件的时候报错:zsh: exec format error: ./ngrok 原因分析: 在Kali Linux上执行./ngrok时出现zsh exec格式错误的问题可能是由于未安装正确版本的ngrok或操作系统不兼容ngrok导致的。以下是一些可能的解…...

<学习笔记>从零开始自学Python-之-常用库篇(十三)内置小型数据库shelve
一、shelve简介: shelve是Python当中数据储存的方案,类似key-value数据库,便于保存Python对象,shelve只有一个open()函数,用来打开指定的文件(字典),会返回一…...

Redis快速上手篇七(集群-六台虚拟机)
Redis集群 主从复制的场景无法吗满足主机单点故障时需要引入集群配置 一般数据库要处理的读请求远大于写请求 ,针对这种情况,我们优化数据库可以采用读写分离的策略。我们可以部 署一台主服务器主要用来处理写请求,部署多台从服务器 &#…...

LeetCode 301. 删除无效的括号【字符串,回溯或BFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
