记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求
已知公式:
t = G + A B F r + B r 2 2 F + A 2 B + G A F ln ( r − A ) + C o n s t t=\frac{G+AB}{F}r+\frac{Br^2}{2F}+\frac{A^2B+GA}{F}\ln (r-A)+Const t=FG+ABr+2FBr2+FA2B+GAln(r−A)+Const
其中
- t 的值为0-1000,每间隔25取一次值
- A=2.12941E-10
- B=0.637224706
- F=1.2652E-08
- G=4.28646E-06
- Const=1.90196E-06
求r的值。
解法
要解这样的方程通常需要用到数值方法。对于这样的复杂方程,我们可以使用牛顿-拉夫逊法来求解。
牛顿-拉夫逊方法的基本思想是:从一个初始猜测值开始,使用函数的导数(或切线的斜率)来更新猜测值,逐步逼近函数的真实零点。
首先,我们需要定义方程和它的导数,然后根据初始值逐渐逼近正确的解。
/*使用牛顿-拉夫逊法来求解。
牛顿-拉夫逊方法的基本思想是:从一个初始猜测值开始,使用函数的导数(或切线的斜率)来更新猜测值,逐步逼近函数的真实零点。
首先,定义方程function和它的导数定义了方程和其导数derivative,然后根据初始值逐渐逼近正确的解。
newtonRaphson函数使用牛顿-拉夫逊方法迭代地逼近方程的根,从一个初始猜测值开始。
*/
#include <stdio.h>
#include <math.h>
// 设置阈值,用于决定函数的值何时足够接近于0
// 当函数的值的绝对值小于这个阈值时,可以认为我们找到了方程的一个解
#define TOLERANCE 1e-6
// 设置去迭代的最大次数,防止无限迭代
#define MAX_ITER 1000double A = 2.12941E-10;
double B = 0.637224706;
double F = 1.2652E-08;
double G = 4.28646E-06;
double Const = 1.90196E-06;// 定义函数
double function(double r, double t) {return (G + A * B) * r / F + B * r * r / (2 * F) + (A * A * B + G * A) * log(r - A) / F + Const - t;
}// 定义函数对r的导数
double derivative(double r) {return (G + A * B) / F + B * r / F + (A * A * B + G * A) / (F * (r - A));
}// 使用牛顿-拉夫逊法求解
double newtonRaphson(double t) {double r = 1.0; // 初始的猜测值for (int i = 0; i < MAX_ITER; i++) {double f = function(r, t); // 函数在当前猜测值处的值double f_prime = derivative(r); // 函数在当前猜测值处的导数值(也就是切线的斜率)// f的绝对值小于阈值,返回r值if (fabs(f) < TOLERANCE)return r;r = r - f / f_prime; // 牛顿-拉夫逊方法中的关键更新步骤,用于寻找函数的零点或根}// 超过迭代的最大次数,返回r值return r;
}int main() {int i=1;for (double t = 25; t <= 1000; t += 25) {printf("第%d次迭代:",i++);double r = newtonRaphson(t);printf("t = %lf, r = %lf\n", t, r);}return 0;
}运行结果:

这里,我随机选择了r = 1.0作为开始迭代的初始值。选择合适的初始猜测值很重要,因为不同的初始值可能会导致不同的收敛结果,或者在某些情况下可能不会收敛。如果r = 1.0不适用于这个方程或特定的t值范围,可能需要根据实际情况调整这个值。
通常,基于对问题的了解和对方程的形状有一定的认识,选择一个合理的初始值是有帮助的。如果不确定最佳的初始猜测值是多少,可以尝试多个值并检查结果的稳定性。
另外,阈值TOLERANCE和最大迭代次数MAX_ITER的值也需要自行根据经验选择。
相关文章:

记录一段帮朋友写的代码,使用牛顿-拉夫逊方法解方程
要求 已知公式: t G A B F r B r 2 2 F A 2 B G A F ln ( r − A ) C o n s t t\frac{GAB}{F}r\frac{Br^2}{2F}\frac{A^2BGA}{F}\ln (r-A)Const tFGABr2FBr2FA2BGAln(r−A)Const 其中 t 的值为0-1000,每间隔25取一次值A2.12941E-10B0.…...

滑动窗口限流算法实现一
固定算法 原理:固定算法是将时间线分隔成固定大小的时间窗口,每个窗口都会有个计数器,用来记录窗口时间范围内的请求总数,如果窗口的请求总数达到最大限定值,会认定流量超限。比如将窗口大小设为1分钟,每分…...

简单明了!网关Gateway路由配置filters实现路径重写及对应正则表达式的解析
问题背景: 前端需要发送一个这样的请求,但出现404 首先解析请求的变化: http://www.51xuecheng.cn/api/checkcode/pic 1.请求先打在nginx,www.51xuecheng.cn/api/checkcode/pic部分匹配到了之后会转发给网关进行处理变成localho…...

EMQX内置Web管理控制台-Dashboard
一、Dashboard概述 EMQX Dashboard官网文档:https://docs.emqx.com/zh/enterprise/v5.1/dashboard/introduction.html 1、简介 EMQX 为用户提供了一个功能强大的内置管理控制台,即 EMQX Dashboard。通过这个控制台的 Web 界面,用户可以轻松监…...
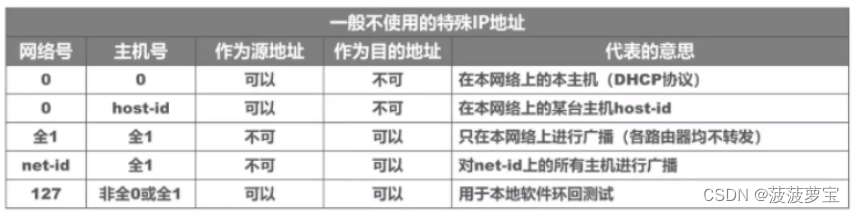
计算机网络重点概念整理-第四章 网络层【期末复习|考研复习】
计算机网络复习系列文章传送门: 第一章 计算机网络概述 第二章 物理层 第三章 数据链路层 第四章 网络层 第五章 传输层 第六章 应用层 第七章 网络安全 计算机网络整理-简称&缩写 文章目录 前言四、网络层4.1 网络层功能4.1.1 电路交换、报文交换与分组交换4.1…...

数组转树形数据
const nodes [{ id: 3, name: 节点C, pid: 1 },{ id: 6, name: 节点F, pid: 3 },{ id: 0, name: root, pid: null },{ id: 1, name: 节点A, pid: 0 },{ id: 8, name: 节点H, pid: 4 },{ id: 4, name: 节点D, pid: 1 },{ id: 2, name: 节点B, pid: 0 },{ id: 5, name: 节点E, p…...

react动态插入样式
在开发组件过程中,偶尔需要动态的插入css,比如在在iframe中渲染组件后,iframe中是没有样式的,所以需要手动插入样式。 插入样式 通常是在useLayoutEffect中动态创建style标签 useLayoutEffect(() > {if (!ref.current) {cons…...
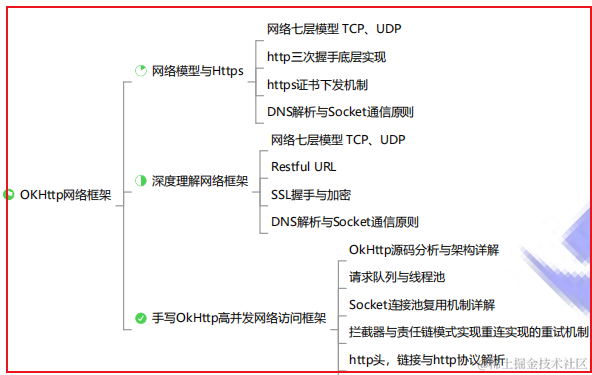
OkHttp网络框架深入理解-SSL握手与加密
OkHttp简介 由Square公司贡献的一个处理网络请求的开源项目,是目前Android使用最广泛的网络框架。从Android4.4开始HttpURLConnection的底层实现采用的是OkHttp。 特点: 支持HTTP/2并允许对同一主机的所有请求共享一个套接字通过连接池,减少了请求延迟…...
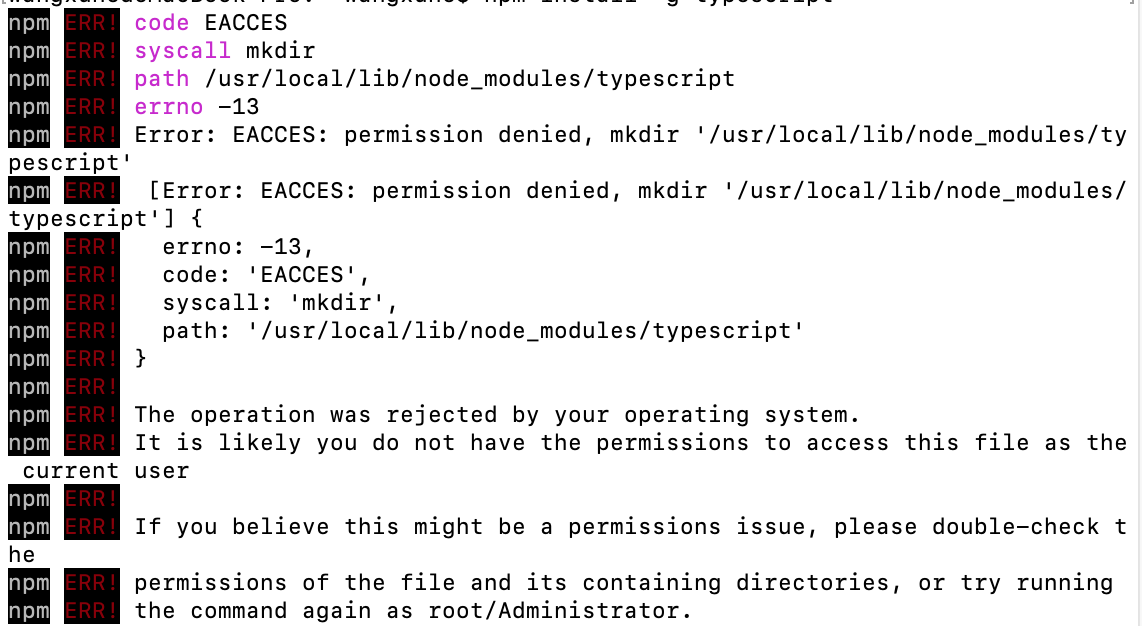
Mac 安装使用NPM及常用命令
环境: Mac 工具: NPM 可通过官网查询一些模块相关 NPM Doc 通过官网文档了解更多的关于NPM的使用 安装 NPM是Node.js的包管理工具,可用于解决 Node.js在代码部署上的问题。 新版本的Node.js已经集成了NPM, 因此可通过下载 Nod…...

利用 JSqlParser 防止 SQL 注入
高手文章《jsqlparser:实现基于SQL语法分析的SQL注入攻击检查》介绍了利用 JSqlParser 防止 SQL 注入,写得很好,只不过有两个问题,代码比较复杂,我于是作了简化,只有两个类;其次检测比较严格,连…...

10.27~10.29数电第三次实验分析与问题
实验要求 分析 寄存器 D触发器有两个输出口,一个输入口,一个时钟信号,一个复位信号 同步异步就是说复位信号在不在always里 给它加一个load就成了一位寄存器, 寄存器堆 8个8位的寄存器堆,每个寄存器都有两读一写…...
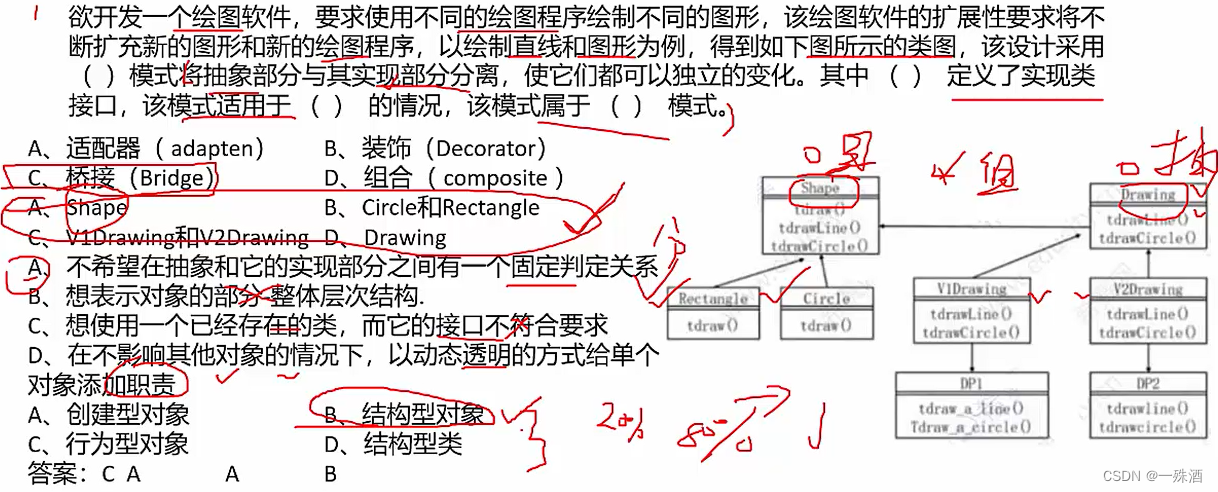
【软考】14.3 设计模式
《设计模式》 有下划线:类模式 / 对象模式无下划线:对象模式 创建型 设计模式 创建对象 构建器(Builder):类和构造分离抽象工厂(Abstract Factory):抽象接口工厂(Factor…...

Mac docker+vscode
mac 使用docker vs code 通过vscode 可以使用docker容器的环境。 可以在容器安装gdb, 直接调试代码。 创建容易时候可以指定目录和容易目录可以共享文件。...
)
LLVM学习笔记(58)
4.4. 目标机器对象 在main()函数的350行,TimeCompilations默认为1,可以通过隐藏的选项“-time-compilations”来指定它的值,它的作用是重复进行指定次数的编译,以得到更好的编译用时数据。而在这个循环中调用的compileModule()&a…...
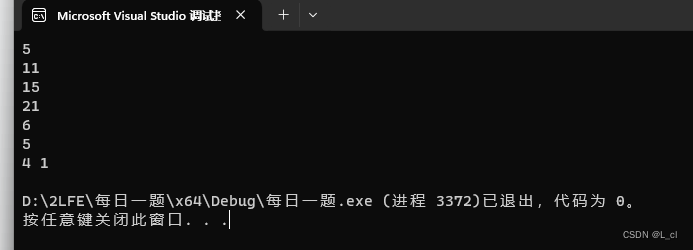
C语言 每日一题 PTA 10.30 day8
1.高空坠球 皮球从某给定高度自由落下,触地后反弹到原高度的一半,再落下,再反弹,……,如此反复。问皮球在第n次落地时,在空中一共经过多少距离?第n次反弹的高度是多少? 输入格式 : …...
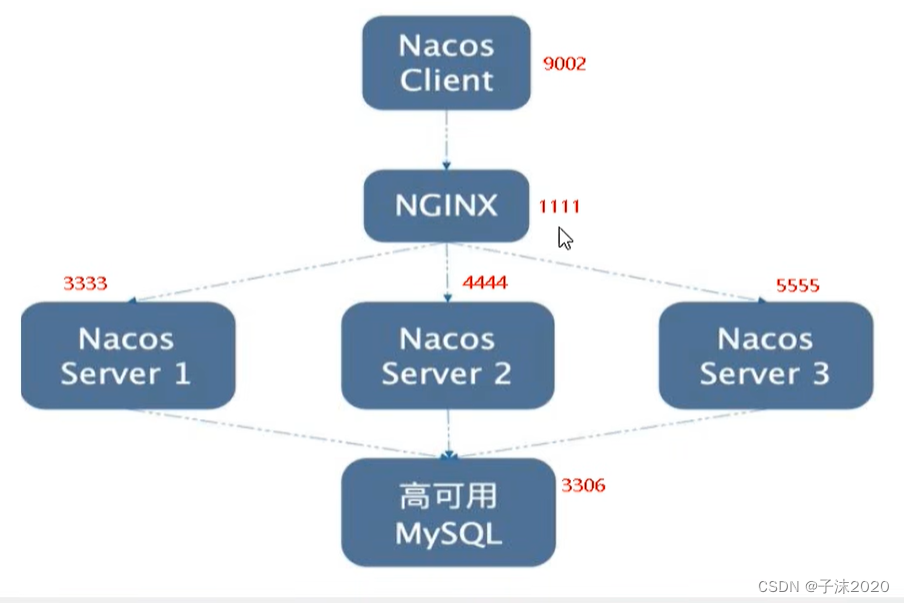
nacos在linux中的安装、集群的配置、mysql生产配置
1.下载和安装 官方下载地址:https://github.com/alibaba/nacos/releases,根据自己需要的本版去下载就行 下载的是 .tar.gz 后缀的文件是linux版本的 使用tar命令解压,完成之后是一个nacos的文件夹 和windows下的文件夹目录是一样的 要启…...

OpenAI 组建安全 AGI 新团队!应对AI“潘多拉魔盒”
夕小瑶科技说 原创 作者 | 小戏 一旦谈及未来 AI,除了天马行空的科幻畅想,不可避免的也有未来 AI 时代的末日预言。从 AI 武器化到 AI 欺骗,从邪恶 AI 到 AI 掌权,人工智能,尤其是通用人工智能的风险始终都清清楚楚的…...
上网行为管理软件有哪些丨功能图文超详细介绍
很多人都在后台问,上网行为管理软件到底是什么,有什么作用,今天就重点给大家讲解一下: 是什么 上网行为管理软件可以帮助企业规范员工的上网行为,提高办公效率,减少潜在威胁。 有哪些 在市面上ÿ…...
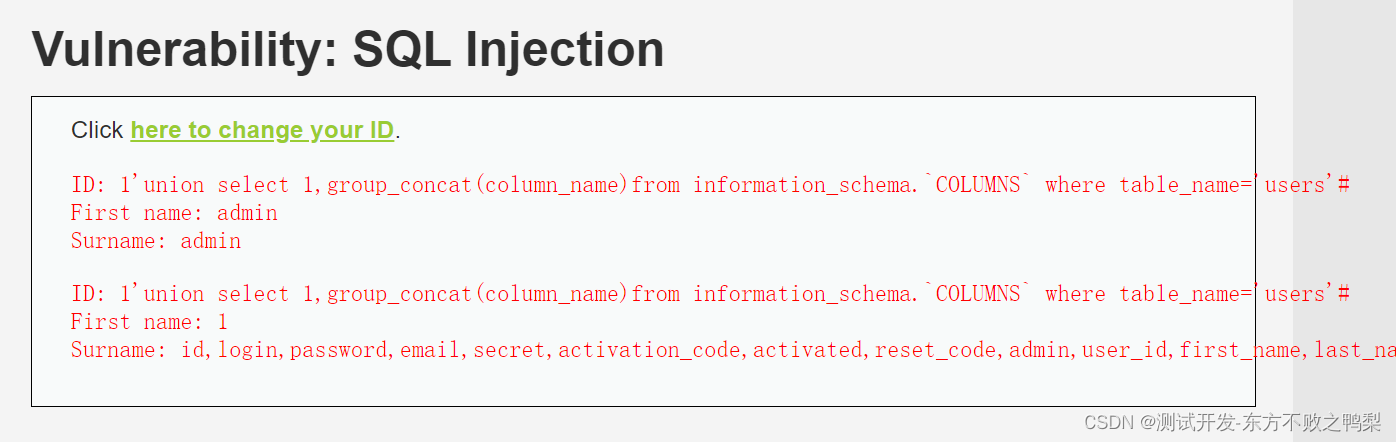
DVWA-SQL Injection SQL注入
概念 SQL注入,是指将特殊构造的恶意SQL语句插入Web表单的输入或页面请求的查询字符串中,从而欺骗后端Web服务器以执行该恶意SQL语句。 成功的 SQL 注入漏洞可以从数据库中读取敏感数据、修改数据库数据(插入/更新/删除)、对数据…...

【0基础学Java第四课】-- 逻辑控制
4. 逻辑控制 4.1 顺序结构4.2 分支结构4.2.1 if语句判断一个数字是奇数还是偶数判断一个数字是正数,负数,还是零判断一个年份是否为闰年 4.2.2 switch 语句 4.3 while循环打印 1 - 10 的数字计算 1 - 100 的和计算 5 的阶乘计算1!2࿰…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
