浮点数和定点数(上):怎么用有限的Bit表示尽可能多的信息?
目录
背景
浮点数的不精确性
定点数的表示
浮点数的表示
小结
背景
在我们日常的程序开发中,不只会用到整数。更多情况下,我们用到的都是实数。比如,我们开发一个电商 App,商品的价格常常会是 9 块 9;再比如,现在流行的深度学习算法,对应的机器学习里的模型里的各个权重也都是 1.23 这样的数。可以说,在实际的应用过程中,这些有零有整的实数,是和整数同样常用的数据类型,我们也需要考虑到。
浮点数的不精确性
那么,我们能不能用二进制表示所有的实数,然后在二进制下计算它的加减乘除呢?先不着急,我们从一个有意思的小案例来看。
你可以在 Linux 下打开 Python 的命令行 Console,也可以在 Chrome 浏览器里面通过开发者工具,打开浏览器里的 Console,在里面输入“0.3 + 0.6”,然后看看你会得到一个什么样的结果。
>>> 0.3 + 0.6
0.8999999999999999
不知道你有没有大吃一惊,这么简单的一个加法,无论是在 Python 还是在 JavaScript 里面,算出来的结果居然不是准确的 0.9,而是 0.8999999999999999 这么个结果。这是为什么呢?
在回答为什么之前,我们先来想一个更抽象的问题。通过前面的这么多讲,你应该知道我们现在用的计算机通常用 16/32 个比特(bit)来表示一个数。那我问你,我们用 32 个比特,能够表示所有实数吗?
答案很显然是不能。32 个比特,只能表示 2 的 32 次方个不同的数,差不多是 40 亿个。如果表示的数要超过这个数,就会有两个不同的数的二进制表示是一样的。那计算机可就会一筹莫展,不知道这个数到底是多少。
40 亿个数看似已经很多了,但是比起无限多的实数集合却只是沧海一粟。所以,这个时候,计算机的设计者们,就要面临一个问题了:我到底应该让这 40 亿个数映射到实数集合上的哪些数,在实际应用中才能最划得来呢?
定点数的表示
有一个很直观的想法,就是我们用 4 个比特来表示 0~9 的整数,那么 32 个比特就可以表示 8 个这样的整数。然后我们把最右边的 2 个 0~9 的整数,当成小数部分;把左边 6 个 0~9 的整数,当成整数部分。这样,我们就可以用 32 个比特,来表示从 0 到 999999.99 这样 1 亿个实数了。
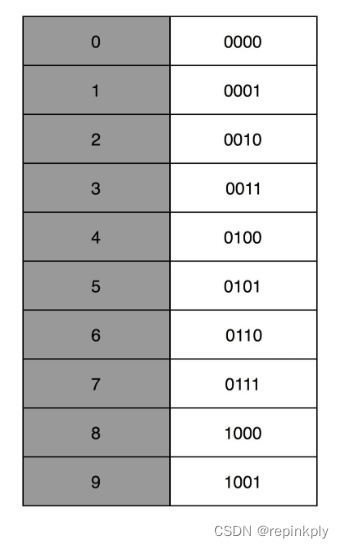
这种用二进制来表示十进制的编码方式,叫作BCD 编码(Binary-Coded Decimal)。其实它的运用非常广泛,最常用的是在超市、银行这样需要用小数记录金额的情况里。在超市里面,我们的小数最多也就到分。这样的表示方式,比较直观清楚,也满足了小数部分的计算。
不过,这样的表示方式也有几个缺点。
第一,这样的表示方式有点“浪费”。本来 32 个比特我们可以表示 40 亿个不同的数,但是在 BCD 编码下,只能表示 1 亿个数,如果我们要精确到分的话,那么能够表示的最大金额也就是到 100 万。如果我们的货币单位是人民币或者美元还好,如果我们的货币单位变成了津巴布韦币,这个数量就不太够用了。
第二,这样的表示方式没办法同时表示很大的数字和很小的数字。我们在写程序的时候,实数的用途可能是多种多样的。有时候我们想要表示商品的金额,关心的是 9.99 这样小的数字;有时候,我们又要进行物理学的运算,需要表示光速,也就是 3×10^8 这样很大的数字。那么,我们有没有一个办法,既能够表示很小的数,又能表示很大的数呢?
浮点数的表示
答案当然是有的,就是你可能经常听说过的浮点数(Floating Point),也就是float 类型。
我们先来想一想。如果我们想在一张便签纸上,用一行来写一个十进制数,能够写下多大范围的数?因为我们要让人能够看清楚,所以字最小也有一个限制。你会发现一个和上面我们用 BCD 编码表示数一样的问题,就是纸张的宽度限制了我们能够表示的数的大小。如果宽度只放得下 8 个数字,那么我们还是只能写下最大到 99999999 这样的数字。

其实,这里的纸张宽度,就和我们 32 个比特一样,是在空间层面的限制。那么,在现实生活中,我们是怎么表示一个很大的数的呢?比如说,我们想要在一本科普书里,写一下宇宙内原子的数量,莫非是用一页纸,用好多行写下很多个 0 么?
当然不是了,我们会用科学计数法来表示这个数字。宇宙内的原子的数量,大概在 10 的 82 次方左右,我们就用 1.0×10^82 这样的形式来表示这个数值,不需要写下 82 个 0。
在计算机里,我们也可以用一样的办法,用科学计数法来表示实数。浮点数的科学计数法的表示,有一个IEEE的标准,它定义了两个基本的格式。一个是用 32 比特表示单精度的浮点数,也就是我们常常说的 float 或者 float32 类型。另外一个是用 64 比特表示双精度的浮点数,也就是我们平时说的 double 或者 float64 类型。
双精度类型和单精度类型差不多,这里,我们来看单精度类型,双精度你自然也就明白了。

单精度的 32 个比特可以分成三部分。
第一部分是一个符号位,用来表示是正数还是负数。我们一般用s来表示。在浮点数里,我们不像正数分符号数还是无符号数,所有的浮点数都是有符号的。
接下来是一个 8 个比特组成的指数位。我们一般用e来表示。8 个比特能够表示的整数空间,就是 0~255。我们在这里用 1~254 映射到 -126~127 这 254 个有正有负的数上。因为我们的浮点数,不仅仅想要表示很大的数,还希望能够表示很小的数,所以指数位也会有负数。
最后,是一个 23 个比特组成的有效数位。我们用f来表示。综合科学计数法,我们的浮点数就可以表示成下面这样:

你会发现,这里的浮点数,没有办法表示 0。的确,要表示 0 和一些特殊的数,我们就要用上在 e 里面留下的 0 和 255 这两个表示,这两个表示其实是两个标记位。在 e 为 0 且 f 为 0 的时候,我们就把这个浮点数认为是 0。至于其它的 e 是 0 或者 255 的特殊情况,你可以看下面这个表格,分别可以表示出无穷大、无穷小、NAN 以及一个特殊的不规范数。
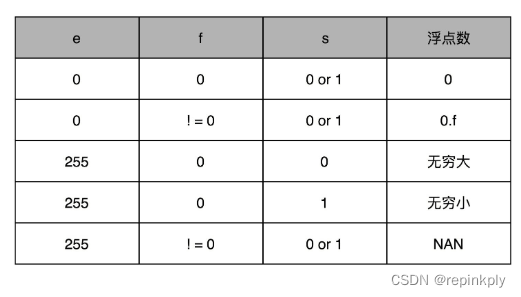
我们可以以 0.5 为例子。0.5 的符号为 s 应该是 0,f 应该是 0,而 e 应该是 -1,也就是

小结
你会看到,在这样的表示方式下,浮点数能够表示的数据范围一下子大了很多。正是因为这个数对应的小数点的位置是“浮动”的,它才被称为浮点数。随着指数位 e 的值的不同,小数点的位置也在变动。对应的,前面的 BCD 编码的实数,就是小数点固定在某一位的方式,我们也就把它称为定点数。
回到我们最开头,为什么我们用 0.3 + 0.6 不能得到 0.9 呢?这是因为,浮点数没有办法精确表示 0.3、0.6 和 0.9。事实上,我们拿出 0.1~0.9 这 9 个数,其中只有 0.5 能够被精确地表示成二进制的浮点数,也就是 s = 0、e = -1、f = 0 这样的情况。
而 0.3、0.6 乃至我们希望的 0.9,都只是一个近似的表达。这个也为我们带来了一个挑战,就是浮点数无论是表示还是计算其实都是近似计算。那么,在使用过程中,我们该怎么来使用浮点数,以及使用浮点数会遇到些什么问题呢?下一讲,我会用更多的实际代码案例,来带你看看浮点数计算中的各种“坑”。
相关文章:

浮点数和定点数(上):怎么用有限的Bit表示尽可能多的信息?
目录 背景 浮点数的不精确性 定点数的表示 浮点数的表示 小结 背景 在我们日常的程序开发中,不只会用到整数。更多情况下,我们用到的都是实数。比如,我们开发一个电商 App,商品的价格常常会是 9 块 9;再比如&…...
一文详解汽车电子LIN总线
0.摘要 汽车电子LIN总线不同于CAN总线。 LIN总线基本上是CAN总线的廉价补充,相比于CAN总线,它提供较低的可靠性和性能。同时LIN总线也是一个应用非常广泛的网络协议,并且越来越受欢迎。 再一次,我们准备了一个关于LIN总线的简要…...
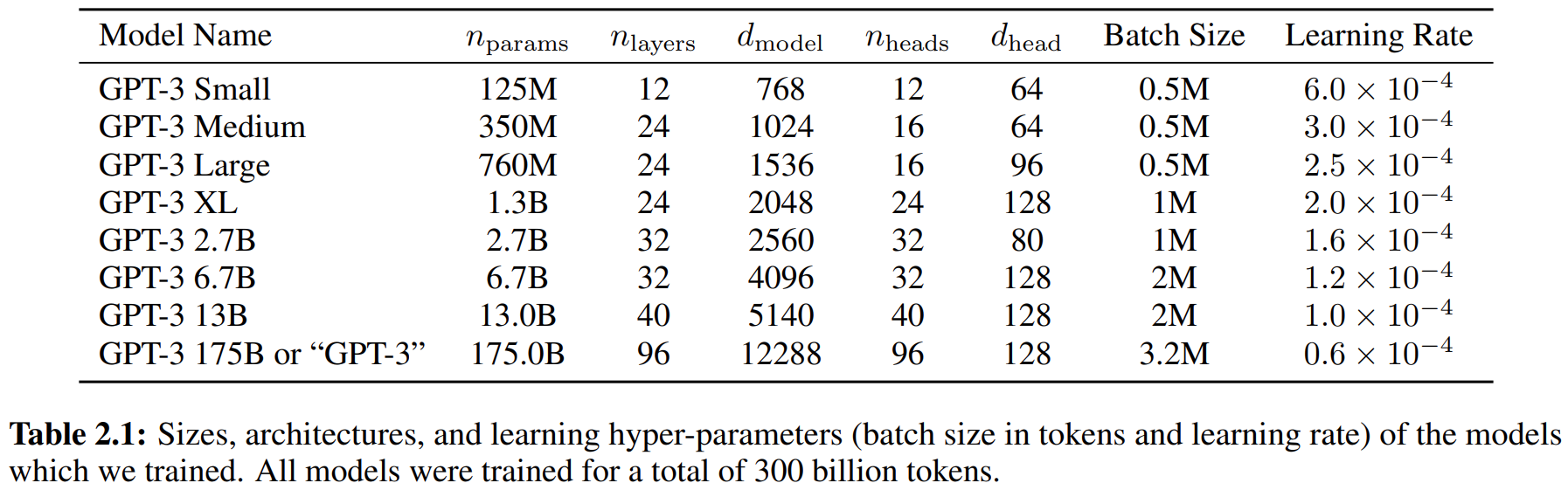
论文阅读——GPT3
来自论文:Language Models are Few-Shot Learners Arxiv:https://arxiv.org/abs/2005.14165v2 记录下一些概念等。,没有太多细节。 预训练LM尽管任务无关,但是要达到好的效果仍然需要在特定数据集或任务上微调。因此需要消除这个…...
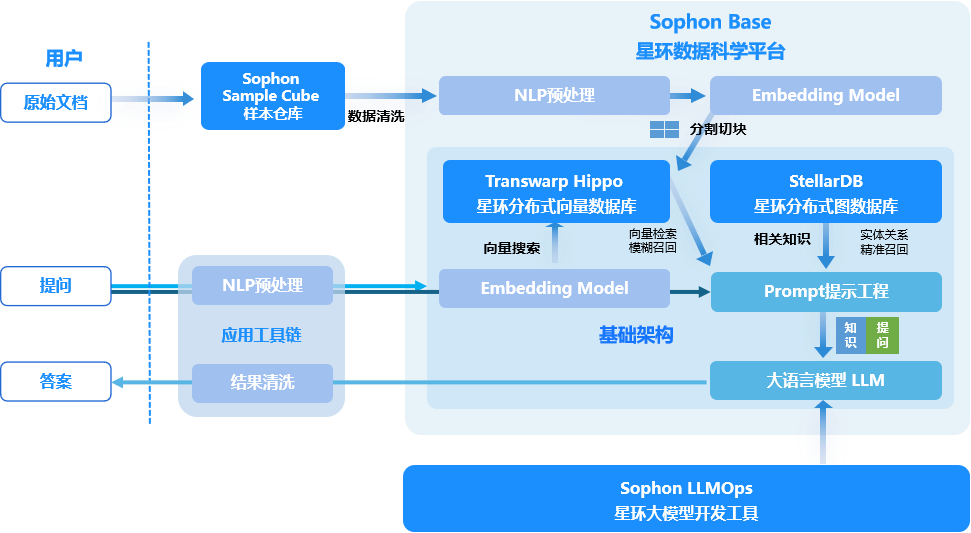
星环科技分布式向量数据库Transwarp Hippo正式发布,拓展大语言模型时间和空间维度
随着企业、机构中非结构化数据应用的日益增多以及AI的爆发式增长所带来的大量生成式数据,所涉及的数据呈现了体量大、格式和存储方式多样、处理速度要求高、潜在价值大等特点。但传统数据平台对这些数据的处理能力较为有限,如使用文件系统、多类不同数据…...
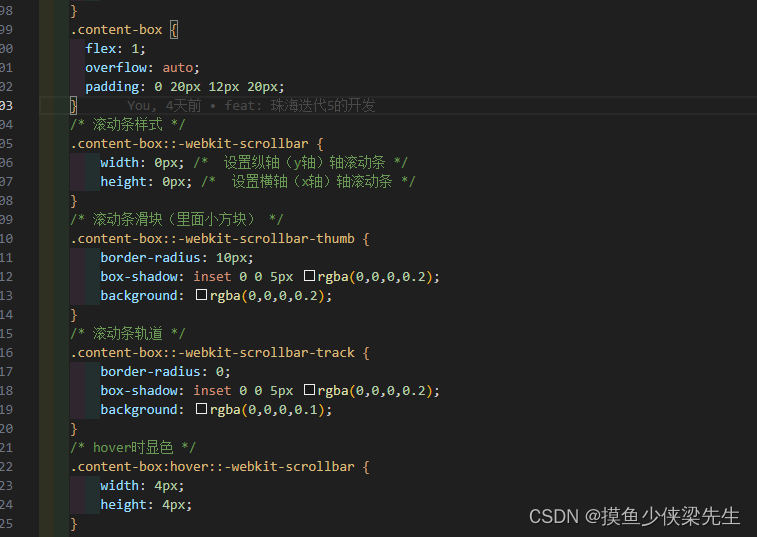
滚动条默认是隐藏的只有鼠标移上去才会显示
效果 在设置滚动条的类名中写 /* 滚动条样式 */.content-box::-webkit-scrollbar {width: 0px; /* 设置纵轴(y轴)轴滚动条 */height: 0px; /* 设置横轴(x轴)轴滚动条 */}/* 滚动条滑块(里面小方块) */.…...
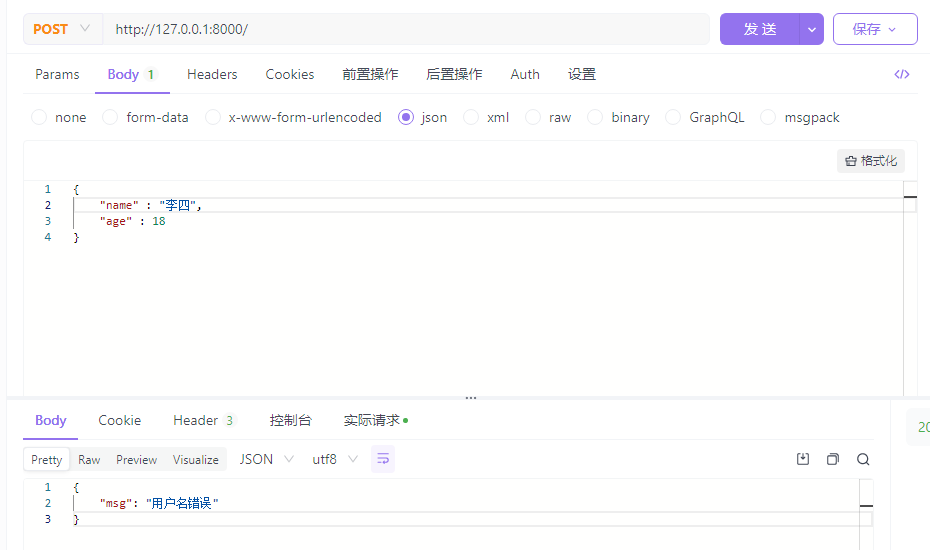
Go学习第十五章——Gin参数绑定bind与验证器
Go web框架——Gin(参数绑定bind与验证器) 1 bind参数绑定1.1 JSON参数1.2 Query参数1.3 Uri绑定动态参数1.4 ShouldBind自动绑定 2 验证器2.1 常用验证器2.2 gin内置验证器2.3 自定义验证的错误信息2.4 自定义验证器 1 bind参数绑定 在Gin框架中&#…...

EtherCAT的4种寻址方式解析
我们知道,一个EtherCAT数据帧(frame)里面包含很多个报文(datagram),不管是什么样式的报文,它们的目的只有一个,就是读写从站寄存器或内存。所以寻址就是以什么方式访问哪个从站的哪个…...
Trino 源码剖析
Functions function 反射和注册 io.trino.operator.scalar.annotations.ScalarFromAnnotationsParser 这里是提取注解元素的方法 String baseName scalarFunction.value().isEmpty() ? camelToSnake(annotatedName(annotated)) : scalarFunction.value(); 这里如果 scala…...

element表格自定义筛选
文章目录 前言一、简介二、效果展示三、源码总结 前言 提示:这里可以添加本文要记录的大概内容: …待续 提示:以下是本篇文章正文内容,下面案例可供参考 一、简介 修改el-table的筛选…待续 二、效果展示 三、源码 使用方法…...

全方位 Linux 性能调优经验总结
Part1Linux性能优化 1性能优化 性能指标 高并发和响应快对应着性能优化的两个核心指标:吞吐和延时 图片来自: www.ctq6.cn 应用负载角度:直接影响了产品终端的用户体验系统资源角度:资源使用率、饱和度等 性能问题的本质就是系统资源已经…...

Linux机器网络检查
查看DNS file: dianTestLRSSnapshot:~$ cat /etc/resolv.conf # This file is managed by man:systemd-resolved(8). Do not edit. # # This is a dynamic resolv.conf file for connecting local clients to the # internal DNS stub resolver of systemd-resolved. This file…...

使用示例和应用程序全面了解高效数据管理的Golang MySQL数据库
Golang,也被称为Go,已经成为构建强大高性能应用程序的首选语言。在处理MySQL数据库时,Golang提供了一系列强大的库,简化了数据库交互并提高了效率。在本文中,我们将深入探讨一些最流行的Golang MySQL数据库库ÿ…...

ubuntu 22.04 源码安装 apollo 8.0
对于其他的关于GPU的安装包需求,这里不再列出,因为我之前安装过,偷个懒就不写了,哈哈哈哈1, 安装docker 安装docker命令(这里的安装命令都是在docker官网,还有安装包): 1, 设置docker的apt仓库 # Add Do…...

RK3588编译MXNet框架
目录 1. 背景 2.编译MXNet准备 3.开发板编译 1. 背景 MXNet(也称为Apache MXNet或incubator-mxnet)是一个开源的深度学习框架,它最初由华为和亚马逊AWS共同开发,并于2017年成为Apache软件基金会的孵化项目。MXNet旨在提供高效、…...

港府Web3宣言周年思考:合规困境中的“隐患”
出品|欧科云链研究院 作者|毕良寰 距离《有关虚拟资产在港发展的政策宣言》已过去一年,我们欧科云链研究院在分析全球几个主要国家和地区对Web3的监管政策及态度后,对港府的雄心壮志充满期待。然而,由于近期一些庞氏骗…...

vue点击按钮跳转页面
在Vue.js中,你可以使用<router-link>或this.$router.push()来实现点击按钮跳转页面的功能,前提是你已经配置了Vue Router。以下是两种不同的方法来实现页面跳转: 方法一:使用<router-link> <router-link> 是Vu…...

大中小企业对CRM系统的需求
在以前,CRM客户管理系统是大型企业的专属。如今,不论何种规模的企业都能够使用CRM系统。市面上的CRM有着丰富的功能类型,管理者可以从企业自身规模出发,选择适合的CRM系统。下面说说,大中小企业对CRM系统的需求。 一句…...

.net core iis 发布后登入的时候请求不到方法报错502
.net core iis 发布后登入的时候请求不到方法报错502 502 bad gateway 502 - Web 服务器在作为网关或代理服务器时收到了无效响应。 您要查找的页面有问题,无法显示。当 Web 服务器(作为网关或代理)与上游内容服务器联系时,收到来自内容服务器的无效…...
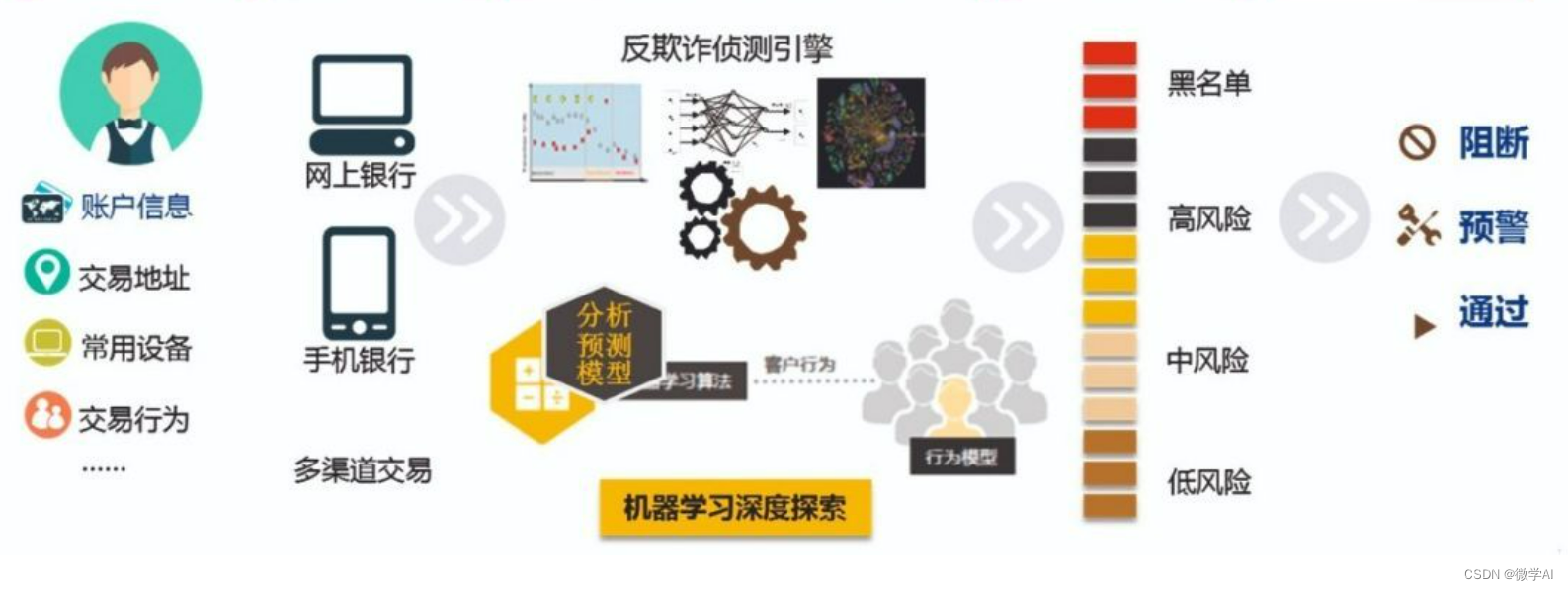
知识图谱实战应用30-知识图谱在反欺诈情报分析项目中的应用实践
大家好,我是微学AI,今天给大家介绍一下知识图谱实战应用30-知识图谱在反欺诈情报分析项目中的应用实践,现代商业环境中,各类欺诈行为日益猖獗,严重影响企业的运营和社会秩序。传统的欺诈检测方法难以满足实时性和有效性方面的要求。本文介绍了采用知识图谱技术构建反欺诈情报…...
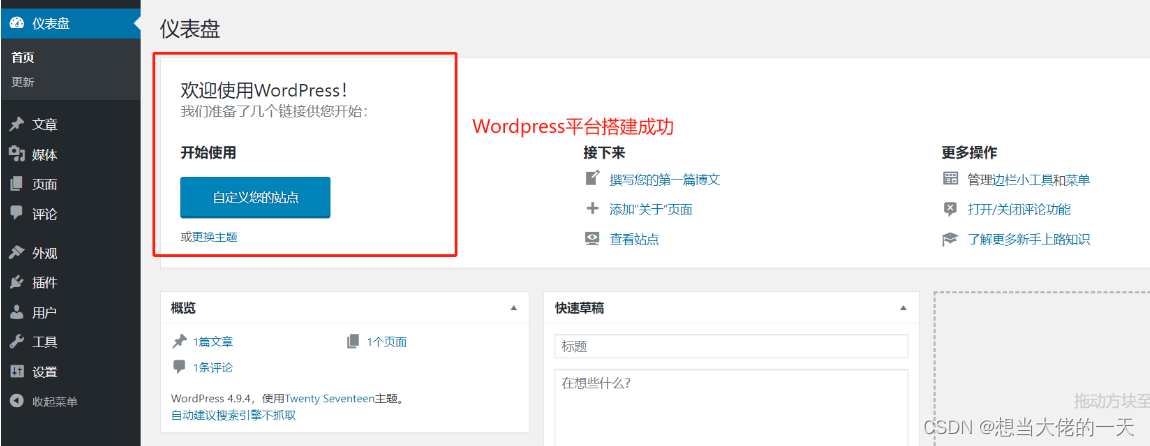
[云原生1. ] 使用Docker-compose一键部署Wordpress平台
文章目录 1. Docker-compose概述1.1 简介1.2 docker-compose 的三大概念1.3 docker-compose配置模板文件常用的字段1.4 docker-compose 常用命令及格式 2. YAML 文件的详细介绍及编写注意事项2.1 简介2.2 yaml的特性2.2.1 语法特点2.2.2 数据结构2.2.3 引号的区别2.2.4 内置类型…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
