NOIP2023模拟6联测27 无穷括号序列
题目大意
小 C C C有一个括号序列 A A A,其长度为 m m m,且序列元素只包含左右括号。他想生成一个无限长的括号序列 B B B,由于 B B B的长度为正无穷,所以其下标可以为任意整数(可以为负)。为了由 A A A生成 B B B,小 C C C采用如下方式:
{ b i = a i , 0 ≤ i < n b i = b i − n , i ≥ n b i = b i + n , i < 0 \begin{cases} b_i=a_i,\qquad 0\leq i<n \\ b_i=b_{i-n},\quad \ i\geq n \\ b_i=b_{i+n},\quad \ i<0 \end{cases} ⎩ ⎨ ⎧bi=ai,0≤i<nbi=bi−n, i≥nbi=bi+n, i<0
无聊的小 C C C还打算以序列 B B B为基础生成无穷个长度为正无穷的括号序列,我们定义 B k B^k Bk代表第 k k k个无穷序列, B 0 = B B^0=B B0=B。对于任意 k ≥ 1 k\geq 1 k≥1,由 B k − 1 B^{k-1} Bk−1生成 B k B^k Bk的方式如下:
{ b i k = b i + 1 k − 1 , b i k − 1 = ‘ ( ’ b i k = b i − 1 k − 1 , b i k − 1 = ‘ ) ’ \begin{cases} b_i^k=b_{i+1}^{k-1}, \quad b_i^{k-1}=‘(’ \\ b_i^k=b_{i-1}^{k-1}, \quad b_i^{k-1}=‘)’ \end{cases} {bik=bi+1k−1,bik−1=‘(’bik=bi−1k−1,bik−1=‘)’
最后,小 C C C有 q q q次询问,每次询问给定的 k , l , r k,l,r k,l,r,求有多少个左括号存在于无穷括号序列 B k B^k Bk中下标位于 [ l , r ] [l,r] [l,r]的元素中。
有 T T T组数据。
1 ≤ n , q ≤ 1 0 5 , 0 ≤ k ≤ 1 0 9 , − 1 0 9 ≤ l ≤ r ≤ 1 0 9 , 1 ≤ T ≤ 10 1\leq n,q\leq 10^5,0\leq k\leq 10^9,-10^9\leq l\leq r\leq 10^9,1\leq T\leq 10 1≤n,q≤105,0≤k≤109,−109≤l≤r≤109,1≤T≤10
时间限制 3000 m s 3000ms 3000ms,空间限制 512 M B 512MB 512MB。
题解
设 f ( k , i ) f(k,i) f(k,i)表示 B k B^k Bk中第 i i i个左括号的下标( i i i可以为 0 0 0甚至负数),设 g ( k , p ) g(k,p) g(k,p)表示满足 f ( k , i ) ≤ p f(k,i)\leq p f(k,i)≤p的最大的 i i i,则区间 [ l , r ] [l,r] [l,r]里的左括号的总数为 g ( k , r ) − g ( k , l − 1 ) g(k,r)-g(k,l-1) g(k,r)−g(k,l−1)。 g g g的值可以用二分求出。
因为我们只关心 g g g的差值,所以第 0 0 0个左括号的位置对应那个左括号其实是可以任意指定的。方便起见,我们把括号序列 A A A中的第一个左括号设为第 0 0 0个左括号。
下面考虑 f ( k , i ) f(k,i) f(k,i)的转移式:
- 如果 f ( k − 1 , i ) f(k-1,i) f(k−1,i)的下一个字符为右括号,因为 ( ) () ()会变成 ) ( )( )(,所以 f ( k , i ) = f ( k − 1 , i ) + 1 f(k,i)=f(k-1,i)+1 f(k,i)=f(k−1,i)+1
- 如果 f ( k − 1 , i ) f(k-1,i) f(k−1,i)的下一个字符为右括号,因为 ( ( (( ((会变成 ( ∗ (* (∗,所以 f ( k , i ) = f ( k − 1 , i + 1 ) − 1 f(k,i)=f(k-1,i+1)-1 f(k,i)=f(k−1,i+1)−1
那么,转移式为
f ( k , i ) = min { f ( k − 1 , i ) + 1 , f ( k − 1 , i + 1 ) − 1 } f(k,i)=\min\{f(k-1,i)+1,f(k-1,i+1)-1\} f(k,i)=min{f(k−1,i)+1,f(k−1,i+1)−1}
假设 f ( k , i ) f(k,i) f(k,i)是从 f ( 0 , j ) f(0,j) f(0,j)转移过来的,那么第一维从 0 0 0走到 k k k的过程中, min \min min中的第二项恰好选了 j − i j-i j−i次,第一项恰好选了 k − ( j − i ) k-(j-i) k−(j−i)次,所以转移式还可以写为
f ( k , i ) = min i ≤ j ≤ i + k { f ( 0 , j ) + k − 2 ( j − i ) } f(k,i)=\min\limits_{i\leq j\leq i+k}\{f(0,j)+k-2(j-i)\} f(k,i)=i≤j≤i+kmin{f(0,j)+k−2(j−i)}
可以看出决策区间的大小为 k k k。设括号序列 A A A中,左括号的数量为 m m m,我们先分析 k ≤ m k\leq m k≤m时如何求解。
设 F ( j ) = f ( 0 , j ) − 2 j F(j)=f(0,j)-2j F(j)=f(0,j)−2j,注意到 f ( 0 , j + m ) − f ( 0 , j ) = n f(0,j+m)-f(0,j)=n f(0,j+m)−f(0,j)=n,则有
F ( j + t ) = F ( j % m + t ) + ( n − 2 m ) × ⌊ j m ⌋ F(j+t)=F(j\% m+t)+(n-2m)\times \lfloor\dfrac jm\rfloor F(j+t)=F(j%m+t)+(n−2m)×⌊mj⌋
其中 t t t是任意非负整数。我们可以用 R M Q RMQ RMQ来预处理 F ( 0 ) F(0) F(0)到 F ( 2 m − 1 ) F(2m-1) F(2m−1),然后把 [ i , i + k ] [i,i+k] [i,i+k]映射到 [ i % m , i % m + k ] [i\%m,i\%m+k] [i%m,i%m+k]求最小值即可。
接下来分析一下 k k k比较大的解法。讨论 n − 2 × m n-2\times m n−2×m的值:
- 如果 n − 2 × m ≥ 0 n-2\times m\geq 0 n−2×m≥0,说明 F ( j + m ) ≥ f ( j ) F(j+m)\geq f(j) F(j+m)≥f(j),因此最小值只存在于 i ≤ j < i + m i\leq j<i+m i≤j<i+m这个范围中
- 如果 n − 2 × m < 0 n-2\times m<0 n−2×m<0,说明 F ( j + m ) < f ( j ) F(j+m)<f(j) F(j+m)<f(j),因此最小值只存在于 i + k − m < j ≤ i + k i+k-m<j\leq i+k i+k−m<j≤i+k这个范围中
这样,我们就把区间长度缩小到了 m m m,通过与上面类似的方法,用 R M Q RMQ RMQ求最小值即可。
时间复杂度为 O ( ∑ ( n log n + q log v ) ) O(\sum(n\log n+q\log v)) O(∑(nlogn+qlogv)),其中 v v v表示 l , r l,r l,r的值域。
可以参考代码帮助理解。
卡常小技巧
如果你 TLE \text{TLE} TLE的话,可以参考一下下面这些卡常小技巧:
- 加上快读
- 在将当前区间映射在 [ 0 , 2 m − 1 ] [0,2m-1] [0,2m−1]上时,因为 i i i有可能为负数,所以会需要用 ( i % m + m ) % m (i\%m+m)\%m (i%m+m)%m,这样模了两次,会比较慢,所以当 i < 0 i<0 i<0时我们可以改为 ( i + i n f × m ) % m (i+inf\times m)\%m (i+inf×m)%m,其中 i n f inf inf是一个很大的数,来保证 i + i n f × m ≥ 0 i+inf\times m\geq 0 i+inf×m≥0;如果 i ≥ 0 i\geq 0 i≥0,则直接用 i % m i\% m i%m。这样就都只需要模一次了,可以快不少
- 在求 S T ST ST表的时候,对二维数组要先枚举行再枚举列,参考这篇博客,这样也可以快很多
code
#include<bits/stdc++.h>
#define rg register
using namespace std;
const int N=100000;
const long long inf=1e9;
int T,n,m,q,lg[2*N+5],f[2*N+5],st[2*N+5][20];
char s[N+5];
int rd(){int t=0,fl=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') fl=-1;ch=getchar();}while(ch>='0'&&ch<='9'){t=t*10+ch-'0';ch=getchar();}return t*fl;
}
void init(){lg[0]=-1;for(rg int i=1;i<=2*N;i++) lg[i]=lg[i/2]+1;
}
void solve(){for(rg int i=0;i<m;i++) f[i+m]=f[i]+n;for(rg int i=0;i<2*m;i++) st[i][0]=f[i]-2*i;for(rg int j=1;j<=17;j++){for(rg int i=0;i+(1<<j)-1<2*m;i++){st[i][j]=min(st[i][j-1],st[i+(1<<j-1)][j-1]);}}
}
int findst(int l,int r){int k=lg[r-l+1];return min(st[l][k],st[r-(1<<k)+1][k]);
}
int sv(int x,int mod){if(x>=0) return x%mod;return (x+inf*mod)%mod;
}
int find(int k,int x){if(k<=m){int md=sv(x,m),tmp=(x-md)/m;return findst(md,md+k)+(n-2*m)*tmp+k+2*x;}else if(n-2*m>=0){int md=sv(x,m),tmp=(x-md)/m;return findst(md,md+m-1)+(n-2*m)*tmp+k+2*x;}else{int md=sv(x+k-m,m),tmp=(x+k-m-md)/m;return findst(md+1,md+m)+(n-2*m)*tmp+k+2*x;}
}
int gt(int k,int x){int l=-inf,r=inf,mid;while(l<=r){mid=l+r>>1;if(find(k,mid)<=x) l=mid+1;else r=mid-1;}return l-1;
}
int main()
{
// freopen("seq.in","r",stdin);
// freopen("seq.out","w",stdout);init();T=rd();while(T--){scanf("%s",s);n=strlen(s);m=0;for(rg int i=0;i<n;i++){if(s[i]=='(') f[m++]=i;}q=rd();if(!m){for(rg int i=1,k,l,r;i<=q;i++){k=rd();l=rd();r=rd();printf("0\n");}continue;}solve();for(rg int i=1,k,l,r;i<=q;i++){k=rd();l=rd();r=rd();printf("%d\n",gt(k,r)-gt(k,l-1));}}return 0;
}
相关文章:

NOIP2023模拟6联测27 无穷括号序列
题目大意 小 C C C有一个括号序列 A A A,其长度为 m m m,且序列元素只包含左右括号。他想生成一个无限长的括号序列 B B B,由于 B B B的长度为正无穷,所以其下标可以为任意整数(可以为负)。为了由 A A A生…...
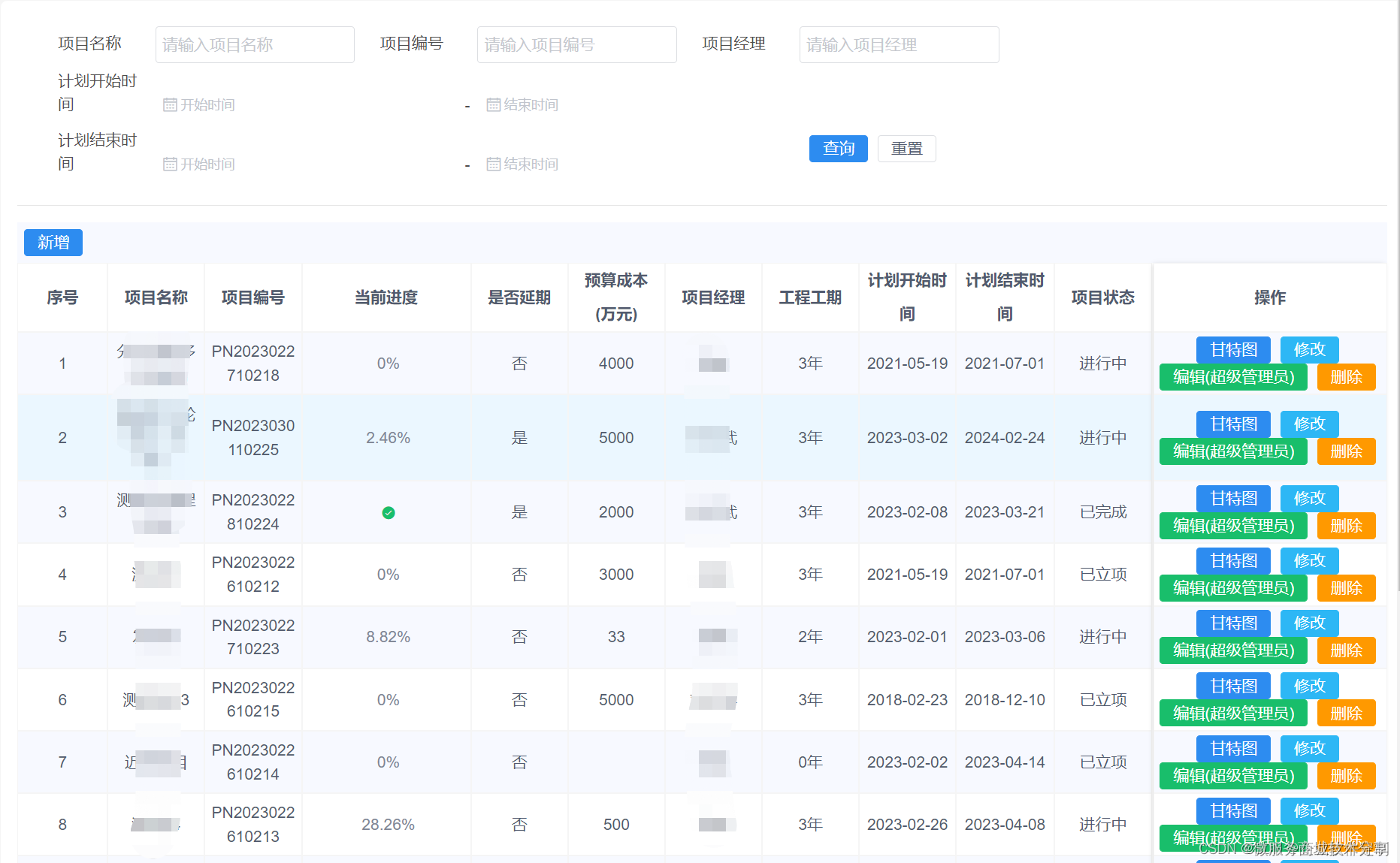
java spring cloud 工程企业管理软件-综合型项目管理软件-工程系统源码
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示…...
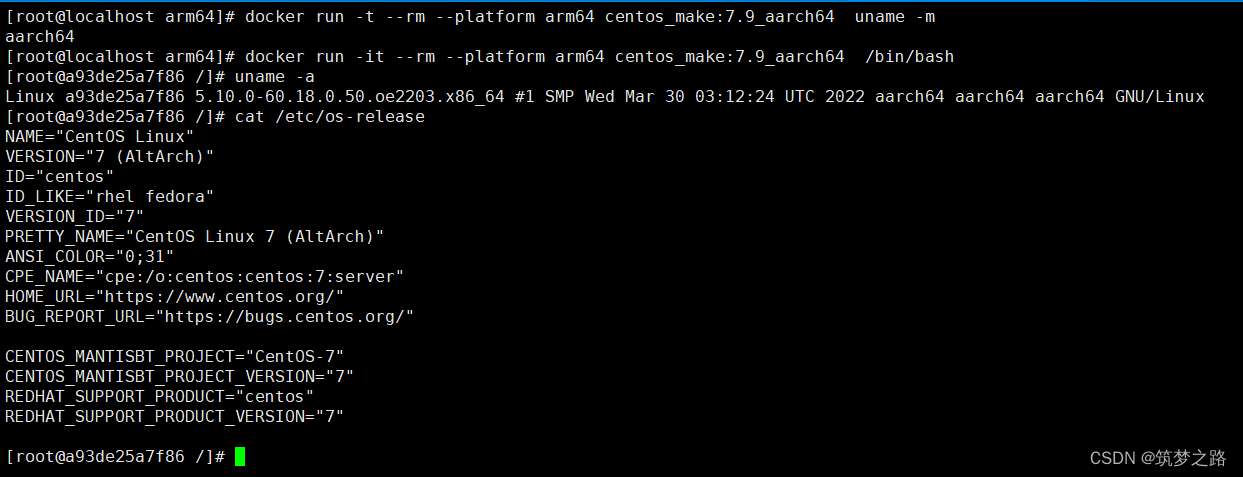
openEuler 22.03 x86架构下docker运行arm等架构的容器——筑梦之路
为什么要这样做? 随着国产化的普及,国家政策对信创产业的支持,尤其一些金融证券行业、政府单位等,逐渐开始走国产化信创的路线,越来越多接触到国产 CPU (arm 平台,比如华为的鲲鹏处理器…...

【Java】HashMap常见的面试题
HashMap常见面试题 1.HashMap key 是否可以是为 我们自定义对象?——可以 2.HashMap 存储数据 有序还是无序?——无序 3.HashMap key 是否可以存放 null值?如果可以的话 存放在 数组中那个位置?——可以;存放在 index0的位置 4.Ha…...
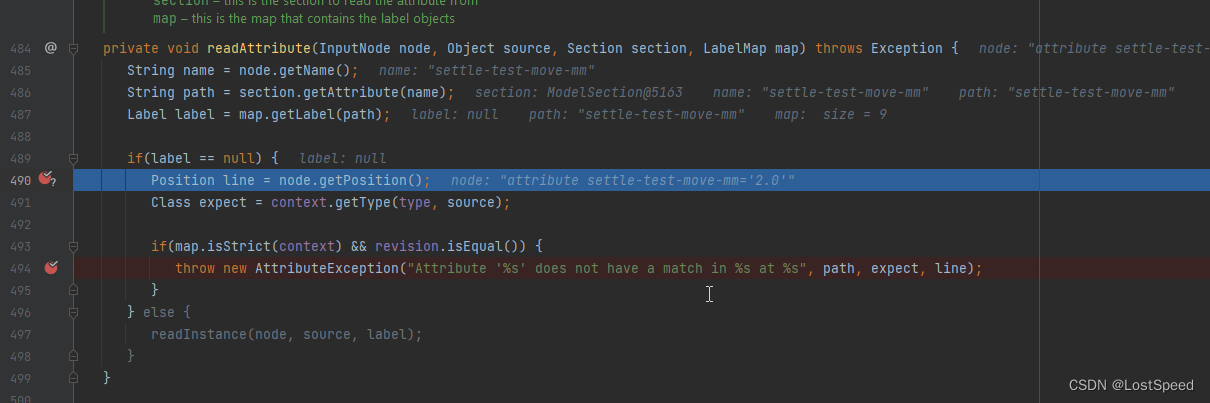
openpnp - src - 配置文件载入过程的初步分析
文章目录 openpnp - src - 配置文件载入过程的初步分析概述笔记自己编译用的git版本报错截图问题1 - 怎么在调试状态下, 定位到抛异常的第一现场?结合单步调试找到的现场, 来分析报错的原因openpnp配置文件读取的流程END openpnp - src - 配置文件载入过程的初步分析 概述 从…...
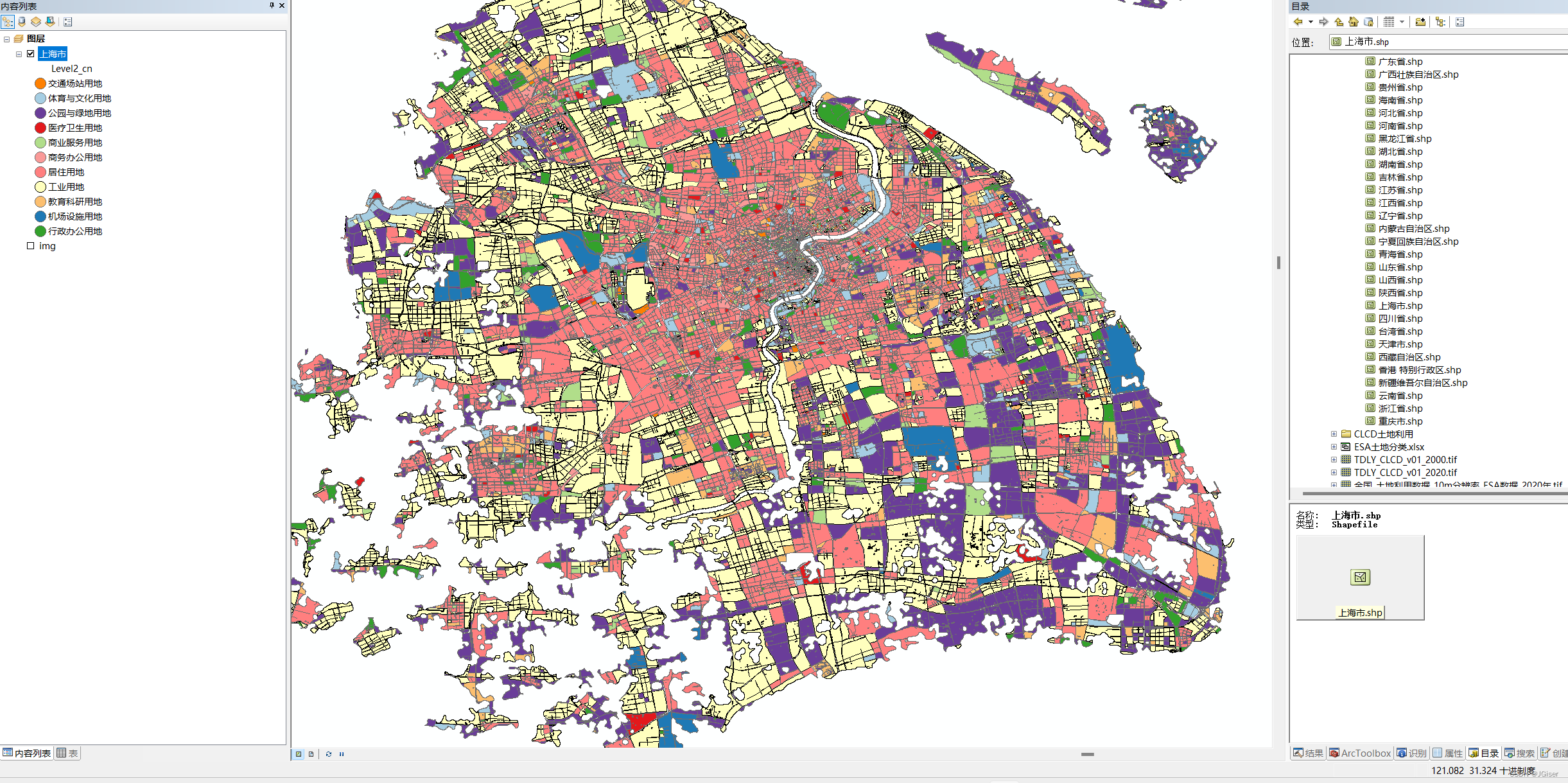
中国各城市土地利用类型(城市功能)数据集(shp)
中国各城市土地利用类型(城市功能)数据集 时间:2018年 全国范围的城市用地类型数据(居住/商业/交通用地等共计11类) 分类:居住用地、商业用地、工业用地、医疗设施用地、体育文化设施用地、交通场站用地、绿地等用地类型 含城市编码、一级分类5个、二级分类11个 数据按…...
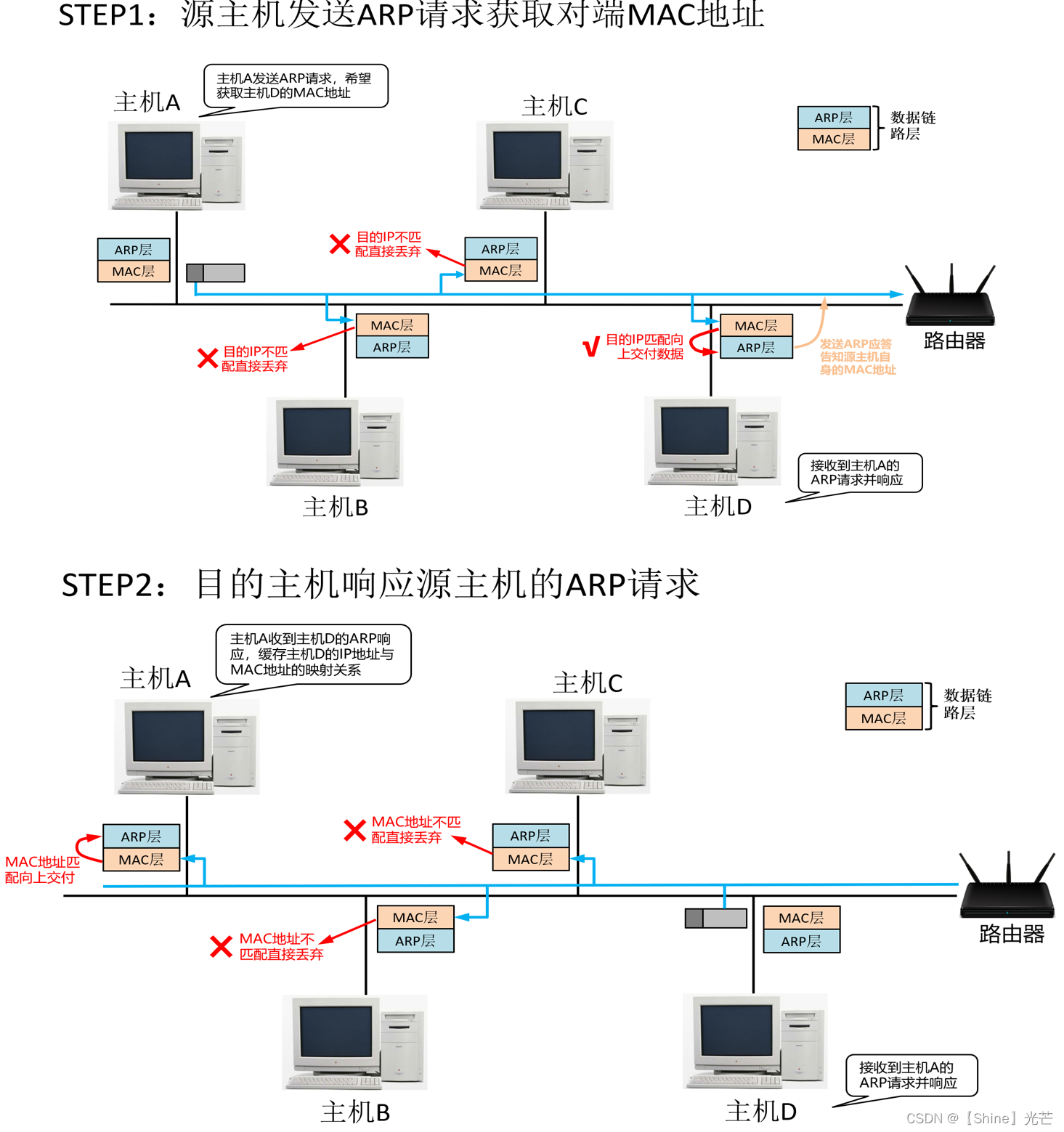
Linux网络编程:数据链路层
目录 一. 数据链路层概述 二. 以太网 2.1 以太网的概念 2.2 以太网数据帧 2.3 对于MAC地址的认识 2.4 数据碰撞问题 三. MTU和MSS 3.1 什么是MTU 3.2 MTU对UDP的影响 3.3 MTU对TCP的影响(MSS的概念) 四. ARP协议 4.1 ARP协议的作用 4.2 ARP数…...

python 线程 超时时间
python 线程 超时时间_mob649e815f0f18的技术博客_51CTO博客...
)
LeetCode:274. H 指数、275. H 指数 II(C++)
目录 274. H 指数 题目描述: 实现代码与解析: 排序暴力 275. H 指数 II 题目描述: 实现代码与解析: 二分 比较简单,不再写解析,注意二分的时候,r指针为n,含义为个数…...

多线程及锁
1.lock锁和synchronized锁的区别。 1:Synchronized 是Java的一个关键字,而Lock是java.util.concurrent.Locks 包下的一个接口; 2:Synchronized 使用过后,会自动释放锁,而Lock需要手动上锁、手动释放锁&am…...

C++ 写一个Data类的注意问题
Data类 声明和定义分离的一些问题 声明里面我们不带缺省参数,定义我们给缺省参数,如下面两段代码: Data.h#pragma once #include<iostream> using namespace std; class Data { public:Data(int year,int month,int day);private:in…...
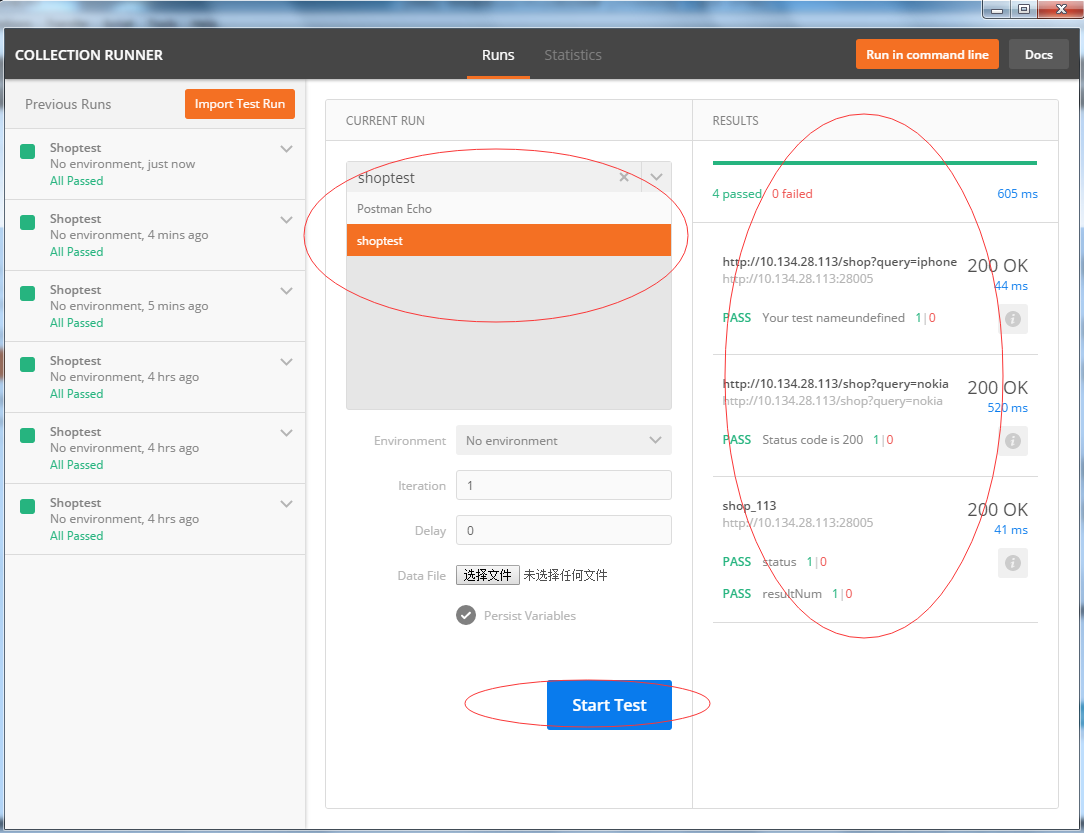
postman做接口测试
之前搞自动化接口测试,由于接口的特性,要验证接口返回xml中的数据,所以没找到合适的轮子,就自己用requests造了个轮子,用着也还行,不过就是case管理有些麻烦,近几天又回头看了看postman也可以玩…...
-29)
hdlbits系列verilog解答(always块)-29
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 由于数字电路由用网线连接的逻辑门组成,因此任何电路都可以表示为模块和赋值语句的某种组合。然而,有时这不是描述电路的最方便方式。过程procedure(其中 always 的块就是一个示例)提供了描述电路的替代语法…...

uniapp实现瀑布流
首先我们要先了解什么是瀑布流: 瀑布流(Waterfall Flow)是一种常见的网页布局方式,也被称为瀑布式布局或砌砖式布局。它通常用于展示图片、博客文章、商品等多个不同大小和高度的元素。 瀑布流布局的特点是每个元素按照从上到下…...
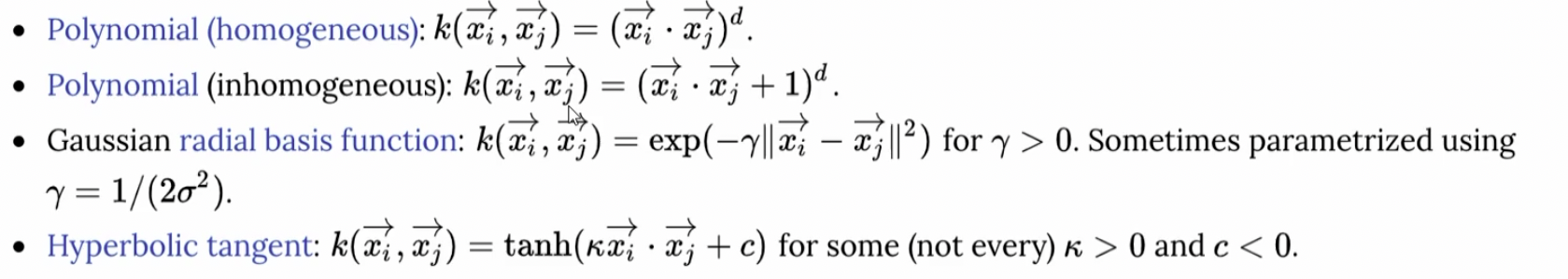
15. 机器学习 - 支持向量机
Hi, 你好。我是茶桁。 逻辑回归预测心脏病 在本节课开始呢,我给大家一份逻辑回归的练习,利用下面这个数据集做了一次逻辑回归预测心脏病的练习。 本次练习的代码在「茶桁的AI秘籍」在Github上的代码库内,数据集的获取在文末。这样做是因为我…...

如何根据进程号查询服务的端口号
ps -ef | grep nacos ps -ef | grep nacos 命令是用于查找系统中所有包含 "nacos" 关键字的进程。这个命令的含义如下: ps: 这是一个用于显示当前正在运行的进程的命令。 -ef: 这两个选项一起使用,表示显示所有进程的详细信息。 -e 选项表示显…...

2.10、自定义量化优化过程
introduction 如何自定义量化优化过程,以及如何手动调用优化过程 code from typing import Callable, Iterableimport torch import torchvision from ppq import QuantizationSettingFactory, TargetPlatform from ppq.api import (ENABLE_CUDA_KERNEL, Quantiz…...

MySQL如何添加自定义函数
深入MySQL:学习如何添加自定义函数 MySQL 是一种流行的开源关系型数据库管理系统,它支持很多内置函数来完成各种操作。不过有时候这些内置函数无法满足我们的需求,这时候就需要自定义函数了。在 MySQL 中,可以通过编写自定义函数…...
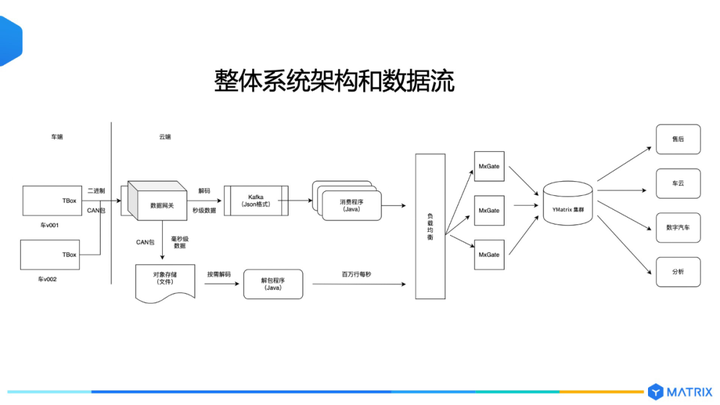
超融合数据库:解锁全场景数据价值的钥匙
前言 近日,四维纵横对外官宣已完成上亿元 B 轮融资。作为超融合数据库理念的提出者,三年来 YMatrix 持续在超融合数据库领域中保持精进与迭代,对于超融合数据库在行业、场景中的应用和理解也更为深刻。 本篇文章,我们将基于 YMa…...
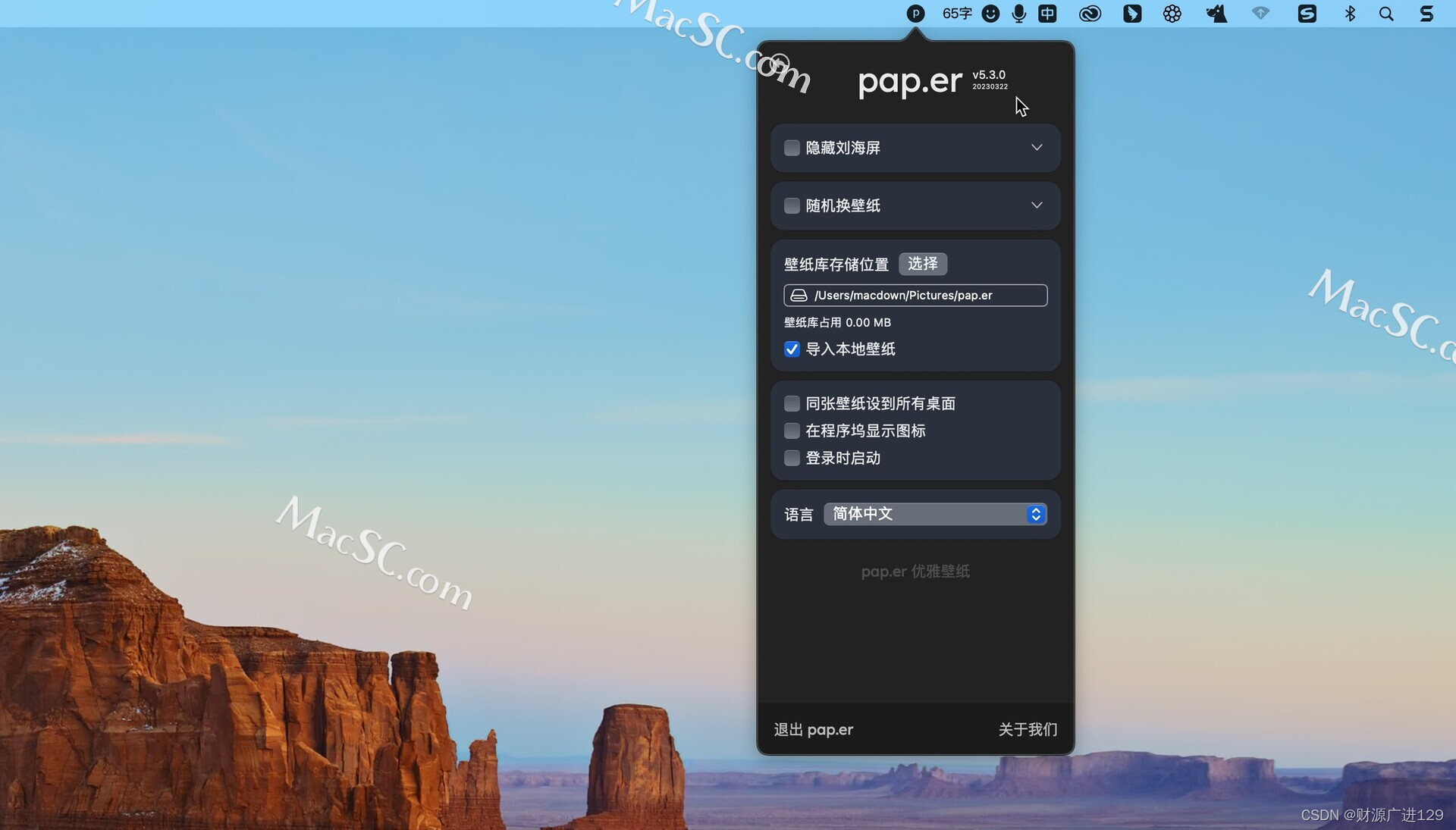
Pap.er for Mac:高清壁纸应用打造你的专属视觉盛宴
在浩瀚的互联网海洋中,你是否曾为寻找一张心仪的高清壁纸而烦恼?或者是在大量的壁纸应用中感到困扰,不知道哪一个能满足你的需求?今天,我要向你介绍的,是一款独特的5K高清壁纸应用——Pap.er for Mac。 Pa…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
