66. 加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入: digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
示例 2:
输入: digits = [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
示例 3:
输入: digits = [0]
输出:[1]
提示:
- 1 <= digits.length <= 100
- 0 <= digits[i] <= 9
class Solution:def plusOne(self, digits: List[int]) -> List[int]:F1=''for i in digits:F1+=str(i)digits1=[]num=str(int(F1)+1)for i in range(len(num)):b=int(num[i])digits1.append(b)return digits1
相关文章:

66. 加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。 示例 1: 输入: digits …...

逻辑(css3)_强制不换行
需求 如上图做一个跑马灯数据,时间、地点、姓名、提示文本字数都不是固定的。 逻辑思想 个人想法是给四个文本均设置宽度,不然会出现不能左对齐的现象。 此时四个文本均左对齐, 垂直排列样式也比较好看,但是出现一个缺点&#…...

营收净利双降、股价下跌四成,敷尔佳带伤闯关“双11”
今年双11预售已经开启,敷尔佳在天猫、抖音等电商平台火热营销;营销热业绩冷,敷尔佳的三季报不及预期。 10月23日,哈尔滨敷尔佳科技发展有限公司(下称“敷尔佳”,301371SZ)公布2023年三季报,其三季度营收净…...

C语言KR圣经笔记 2.8自增和自减 2.9位运算 2.10赋值
2.8 自增和自减操作符 C提供了两个不同寻常的操作符,用于对变量进行自增和自减。自增操作符对操作数加上1,而自减操作符 -- 对操作数减去1。我们已经频繁使用 对变量进行自增,如: if (c \n)nl; 不寻常之处在于 和 -- 既能用作…...
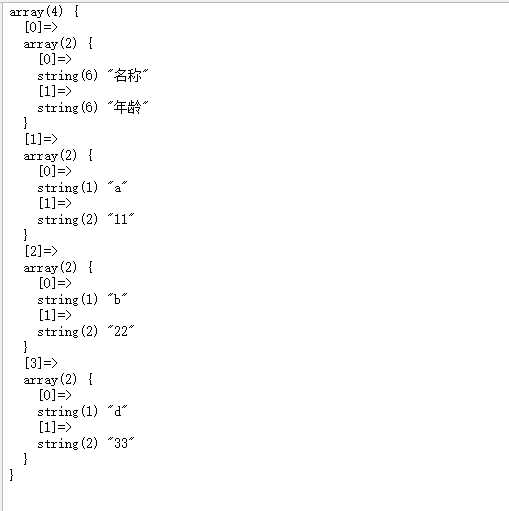
PHP的Excel导出与导入
下载地址(注意php版本大于7.3可能会报错) GitHub - PHPOffice/PHPExcel: ARCHIVED 解压 1、导出 Excel $data[[name>a,age>11],[name>b,age>22],[name>d,age>33], ]; $fileds["name">"名称","age"…...
Ubuntu自建git服务器
Ubuntu 安装 gitlab-ce sudo apt-get update sudo apt-get install gitlab-ce 安装成功 sudo apt-get install gitlab-ce 正在读取软件包列表... 完成 正在分析软件包的依赖关系树 正在读取状态信息... 完成 下列【新】软件包将被安装:gitlab-ce 升…...
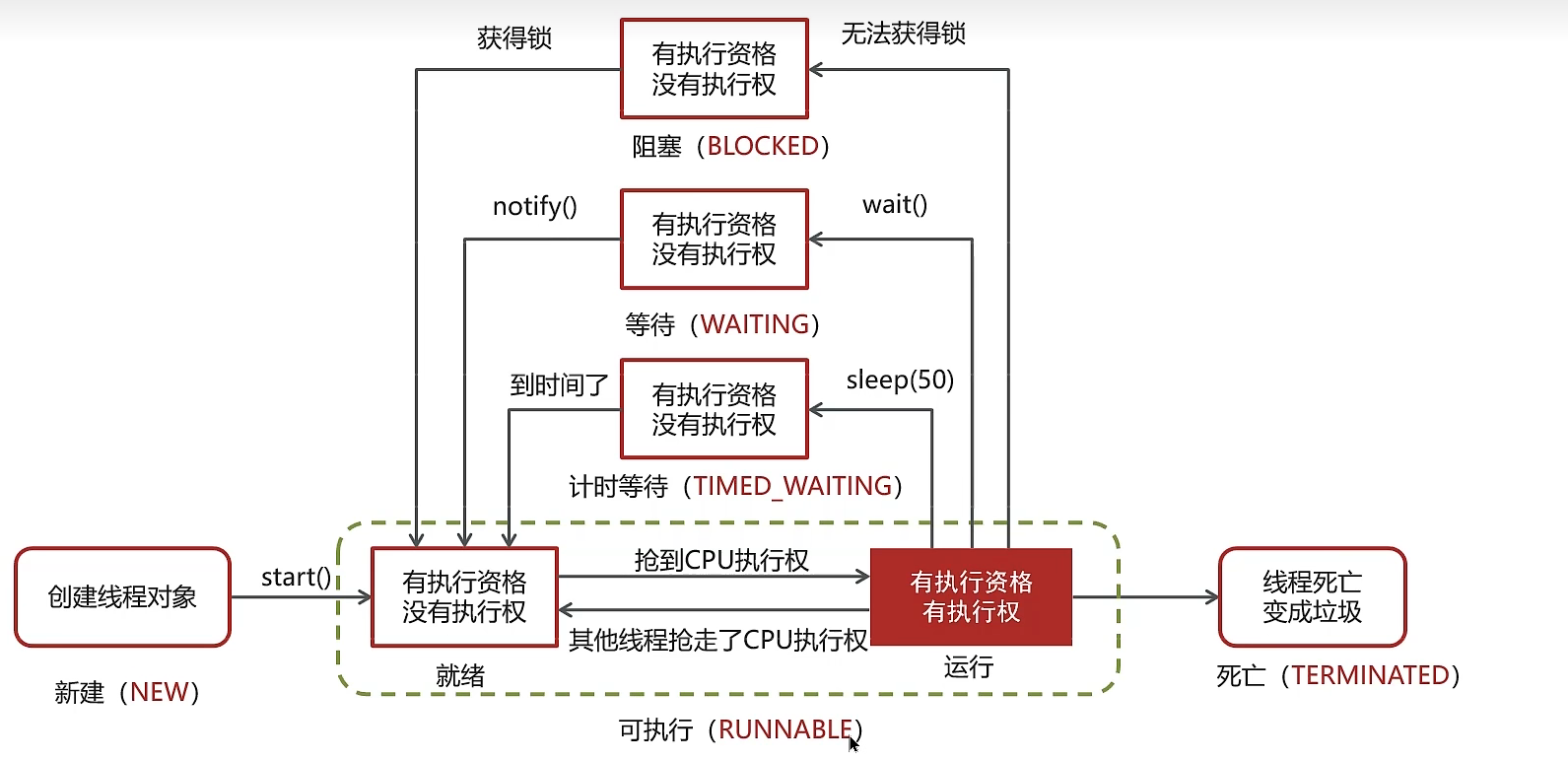
【面试专题】并发编程篇①
📃个人主页:个人主页 🔥系列专栏:Java面试专题 1.线程和进程的区别 线程和进程都是操作系统中的概念,它们的主要区别如下: 资源分配:进程是操作系统中的资源分配的基本单位,每个进程…...

Linux Centos7安装后,无法查询到IP地址,无ens0,只有lo和ens33的解决方案
文章目录 前言1 查看network-scripts目录2 创建并配置 ifcfg-ens33 文件3 禁用NetworkManager4 重新启动网络服务总结 前言 在VMware中,安装Linux centos7操作系统后,想查询本机的IP地址,执行ifconfig命令 ifconfig结果如下: 结…...

行为型模式-访问者模式
在访问者模式中,我们使用了一个访问者类,它改变了元素类的执行算法。通过这种方式,元素的执行算法可以随着访问者改变而改变。这种类型的设计模式属于行为型模式。根据模式,元素对象已接受访问者对象,这样访问者对象就…...

go-kit中如何开启websocket服务
在Go-Kit中,可以使用github.com/go-kit/kit/transport/http包来开启WebSocket服务。以下是一个简单的示例代码,演示了如何在Go-Kit中开启WebSocket服务: package mainimport ("context""fmt""net/http""…...

私有网络的安全保障,WorkPlus Meet内网视频会议助力企业高效会议
在企业内部沟通与协作中,视频会议成为了一种必不可少的沟通方式。然而,传统的互联网视频会议往往受制于网络不稳定因素,给企业带来不便与困扰。WorkPlus Meet作为一款专注内网视频会议的软件,致力于为企业打造高效、稳定的内网视频…...
国际权威媒体聚焦:孙宇晨和波场TRON在迪拜荣获加密行业重磅奖项
近日,在迪拜举行的区块链生态大会(Blockchain Life Conference)上,波场TRON创始人、火币HTX全球顾问委员会委员孙宇晨斩获“年度加密企业家”称号,波场TRON荣膺“年度最佳 Layer 1”大奖。这一消息迅速得到彭博社、雅虎财经、美联社和法国最大媒体之一Le Figaro等国际权威媒体的…...

新闻详情。
<!DOCTYPE html> <html><head><title>新闻</title><meta http-equiv"content-type" content"text/html; charsetutf-8"/><meta name"apple-mobile-web-app-capable" content"yes"/><lin…...
)
Java面试题-Redis-第二天(Redis持久化、过期键删除策略、内存淘汰策略)
目录 一、Redis持久化机制 二、Redis过期键删除策略 三、Redis内存淘汰策略 一、Redis持久化机制 为了能重用Redis数据,防止系统故障造成数据丢失,我们就需要将Redis中的数据写入到磁盘中,也就是持久化 1. 有哪些方式 有rdb和aof两种方式…...
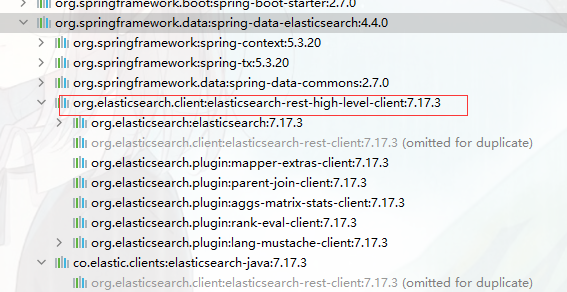
ElasticSearch快速入门实战
全文检索 什么是全文检索 全文检索是一种通过对文本内容进行全面索引和搜索的技术。它可以快速地在大量文本数据中查找包含特定关键词或短语的文档,并返回相关的搜索结果。全文检索广泛应用于各种信息管理系统和应用中,如搜索引擎、文档管理系统、电子…...

揭秘MySQL数据同步至Elasticsearch的最佳方案与技巧
本文介绍下当前常见的场景之一:Mysql数据同步Elasticsearch的实现方案,这里以电商为例,其实所有相关搜索内容都可以使用此方案。 对于搜索,应该是所有APP必备的基础功能,不同时期有不同的解决方案,本次重点…...

正点原子嵌入式linux驱动开发——Linux RTC驱动
RTC也就是实时时钟,用于记录当前系统时间,对于Linux系统而言时间是非常重要的,就和使用Windows电脑或手机查看时间一样,在使用Linux设备的时候也需要查看时间。本章就来学习一下如何编写Linux下的RTC驱动程序。 Linux内核RTC驱动…...

基于EasyCVR技术的大数据视频汇聚与智能分析平台设计方案
一、背景需求 大数据中心的数据建设如火如荼,针对其中城市中的视频监管及算法分析,各卡口监控、治安监控,电警监控不同网络、不同地域,如何进行视频融合、进行统一监管,则是大数据中心解决方案数据汇聚的重中之重。 现…...

骨传导耳机到底好用吗,到底骨传导耳机是不是噱头呢?
随着社会的飞速发展以及科技的不断提升,人们对健康的关注度也逐渐提高起来。而在这种背景下,骨传导耳机以其独特不可替代的优势,吸引了一大群骨传导爱好者的目光。 那么骨传导耳机是不是噱头呢?其实这种耳机不仅不会堵塞耳道&…...

bitsandbytes 遇到CUDA Setup failed despite GPU being available.
使用conda 管理环境时加载大模型会遇到bitsandbytes无法识别cuda的情况: 此处windows系统: pip install bitsandbytes-windowslinux 系统: 将bitsandbytes版本降低至0.39.0 pip install bitsandbytes0.39.0...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
