编码的基本概念
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。
文章目录
- 信源编码
- 分类
- 前缀条件
码符号C表示的是编码的字符集。如二进制编码,c:{0,1} (无特殊说明,本章所有编码都是二进制编码);
信源编码就是将信源符号序列按照一定的数学规律映射成由码符号组成的码序列的过程。
- 信源编码器输入的消息序列:
X=(X1X2…Xl…XL),Xl∈{a1,…an}\boldsymbol{X}=(X_{1} X_{2} \ldots X_{l} \quad \ldots X_{L}) , X_{l} \in\{a_{1}, \ldots a_{n}\} X=(X1X2…Xl…XL),Xl∈{a1,…an}
输入的消息总共有 nLn^{L}nL 种可能的组合
-
输出的码字 (码序列) 为:
Y=(Y1Y2…Yk…YK),Yk∈{b1,…bm}\begin{array}{l} Y=(Y_{1} Y_{2} \ldots Y_{k} \ldots Y_{K}), Y_{k} \in\{b_{1}, \ldots b_{m}\} \end{array} Y=(Y1Y2…Yk…YK),Yk∈{b1,…bm}
输出的码字总共有 mKm^{K}mK种可能的组合。
信源编码
将信源输出符号X, 经信源编码器后变换成另外的压缩符号Y, 然后将压缩后信息经信道传送给信宿。
信源符号之间存在分布不均匀和相关性,使得信源存在冗余度,信源编码的主要任务就是减少冗余,提高编码效率。
针对信源输出符号序列的统计特性, 寻找一定的方法把信源输出符号序列变换为最短的码字序列。
分类
分组码和非分组码
1.分组码: 信源序列在进入编码器之前先分成若干信源符号组(也称信源字),将信源编码器根据一定的规则用码符号序列(也称码字)表示信源字作为编码器的输出。
2.非分组码: 信源序列连续不断地从编码器的输入端进入,同时在编码器的输出端连续不断的产生码序列。

例 信源符号X={a1,a2,a3,a4}X=\{a_{1}, a_{2}, a_{3}, a_{4}\}X={a1,a2,a3,a4}对应不同码字如表
该信源的信息熵为:1.75 bit/symbol
等长码:码中所有码字的长度都相同,如:码0
变长码;码中的码字长短不一,如:码1、2、3、4
非奇异码:信源符号与码字是一一对应的,如:码0、2、3、4
奇异码:信源符号与码字不是一一对应的,如:码1
唯一可译码: 任意有限长的码元序列,只能被唯一地分割成一个个的码字。如码0、3、4。
例:{0,10,11}是一种唯一可译码。
任意一串有限长码序列,如100111000,只能被分割成 10,0,11,10,0,0。任何其他分割法都会产生一些非定义的码字。
奇异码不是唯一可译码
非奇异码
- 唯一可译码,如: 码3;
- 非唯一可译码,如:码2;
-
非即时码(延长码)
如果接收端收到一个完整的码字后不能立即译码,还需等下一个码字开始接收后才能判断是否可以译码,如:码 3;在延长码中有的码是唯一可译的取决于码的总体结构。 -
即时码 (非延长码 ) (异前缀码 )
在译码时无需参考后续的码符号就能立即 作出判断 译成对应的信源符号。如:码 0 、 4
任意一个码字都不是其它码字的 前缀 部分——前缀条件。
可以证明,一种可唯一译码并且具有即时性的编码方法必定满足前缀条件。
前缀条件
任意一个码字都不是其它码字的前缀部分----前缀条件。
如:码0: 00、01、10、11。码4: 1、01、001、0001
可以证明,一种可唯一译码并且具有即时性的编码方法必定满足前缀条件。
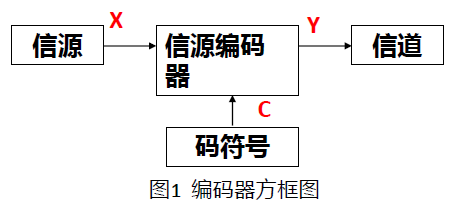
判断码:000、001、01、10是否唯一可译?是否是即时码?
由上图可知,都是。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.
相关文章:
编码的基本概念
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录信源编码分类前缀…...

函数指针与指针函数的区别
目录:一、函数指针1 函数类型2 函数指针(指向函数的指针)3 函数指针数组二.函数指针和指针函数比较1 定义不同2 写法不同3.用法不同三.函数指针做函数参数(回调函数)1 利用回调函数实现打印任意类型数据2 提供能够打印任意类型数组函数3 利用回调函数 提供查找功能四…...

死锁的四个必要条件以及如何避免死锁
死锁的四个必要条件以及如何避免死锁 一.什么是死锁?二.死锁的四个必要条件 1.互斥条件:2.请求与保持条件:3.不剥夺条件:4.循环等待条件: 三.如何避免死锁 1.破坏请求保持条件2.破坏不剥夺条件3.破坏循环等待条件 死锁的四个必要条件以及如…...
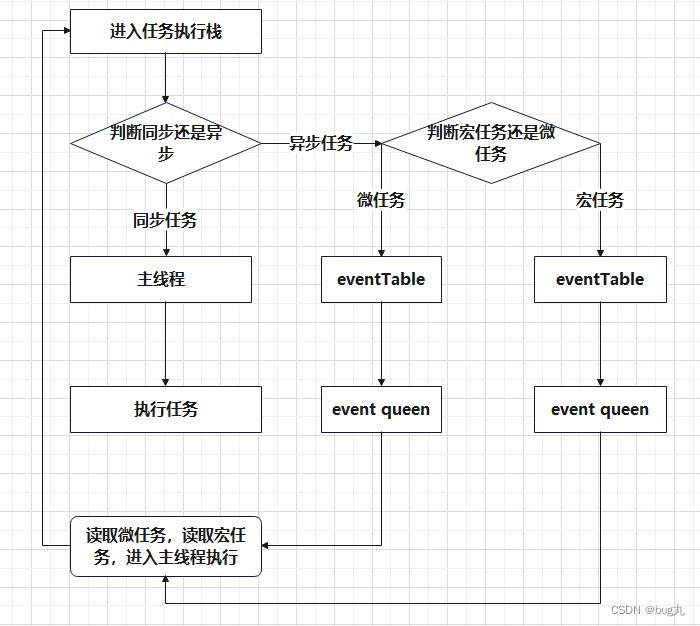
浏览器多线程到事件循环机制
浏览器与js运行机制 进程与线程 进程 进程是CPU分配资源的最小单位,它是一个可以自己独立运行且拥有自己资源空间的任务程序;包括程序以及程序所使用的内存及系统资源 线程 线程是CPU调度的最小单位,它就是程序中的一个执行流࿱…...
Lambda表达式的本质
一直想写一篇文章,来总结lambda表达式,但是之前感觉总结的不是特别到位,现在看了几篇文章和视频后,感觉对lambda表达式有了比较深刻的认识,现在进行记录总结如下: lambda表达式又叫做匿名函数,…...

类的加载过程(生命周期)
类的加载过程(生命周期) 一、装载:通过一个类的全限定名获取定义此类的二进制字节流将这个字节流所代表的静态存储结构转化为方法区的运行时数据结构在内存中生成一个代表这个类的java.lang.Class对象(将字节码加载到内存中),作为…...

2023最新谷粒商城笔记之MQ消息队列篇(全文总共13万字,超详细)
MQ消息队列 其实队列JDK中本身就有,不过这种队列也只能单体服务可能会使用,一旦项目使用的分布式架构,那么一定还是需要用到一个消息中间件的。我们引入消息队列的原因就是对我们的页面相应速度再优化,让用户的体验更好ÿ…...
多变量线性回归模型
多变量线性回归模型 模型参数为n1维向量,此时模型公式为 hθ(x)θ0x0θ1x1θ2x2...θnxnh_{\theta}(x)\theta_{0}x_{0}\theta_{1}x_{1}\theta_{2}x_{2}...\theta_{n}x_{n} hθ(x)θ0x0θ1x1θ2x2...θnxn 可以简化为 hθ(x)θTXh_{\theta}(x)\th…...
php 基于ICMP协议实现一个ping命令
php 基于ICMP协议实现一个ping命令 网络协议是什么ICMP 协议什么是ICMP?ICMP 的主要功能ICMP 在 IPv4 和 IPv6 的封装Wireshark抓包ICMP 请求包分析PHP构建 ICMP 数据包php中的 pack & unpack 函数字节和字符packunpackICMP计算校验和步骤总结网络协议是什么 网络协议&…...

Java基本数据类型
1.概述 佛说,大千世界,无奇不有。在这个世界里,物种的多样性,遍地开花,同样,在Java的世界里,也有着异曲同工之妙,Java秉承面向对象的特性,必然少不了区分对象的类型&…...

English Learning - L2 语音作业打卡 Day2 2023.2.22 周三
English Learning - L2 语音作业打卡 Day2 2023.2.22 周三💌 发音小贴士:💌 当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音[ ɑː ]&…...

45. 跳跃游戏 II
题目: 45. 跳跃游戏 II难度中等1974收藏分享切换为英文接收动态反馈给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 num…...
)
应届生Java面试50题线程篇(含解析)
什么是线程? 答:线程是操作系统能够进行运算调度的最小单位,是程序执行流的最小单元。在Java中,可以通过实现Runnable接口或继承Thread类来创建线程。 创建线程的方式有哪些?各自的优缺点是什么? 继承 Thread 类&…...
【数据库】第七章 数据库设计
第七章数据库设计 数据库设计概述 数据库设计的基本步骤 需求分析概念结构设计逻辑结构设计物理结构设计数据库实施数据库运行和维护 需求分析 收集需求,理解需求 收集各个角色的需求 概念数据库设计 建立概念模型 ,E-R图/IDEF1x图 消除冲突&…...

Burp Suite 常用模块简介
Burp Suite 常用模块分为 目标站点(target)模块 代理(proxy)模块 攻击(Intruder)模块 重放(Repeater) 模块 Target模块是对站点资源的收集,与站点各资源包发出和相应包的记录 Proxy模块是核心模块,可以拦截数据包发送往浏览器,进行修改后再…...

QML Item和Rectangle详解
1.Item和Rectangle Item类型是Qt Quick中所有可视项的基本类型。 Qt Quick中的所有可视项都继承Item。尽管Item对象没有视觉外观,但它定义了视觉项中常见的所有属性,例如x和y位置、宽度和高度、锚定和键处理支持。 Rectangle继承自Item,多…...
(六))
常见前端基础面试题(HTML,CSS,JS)(六)
GET 和 POST 的区别 从 http 协议的角度来说,GET 和 POST 它们都只是请求行中的第一个单词,除了语义不同,其实没有本质的区别。 之所以在实际开发中会产生各种区别,主要是因为浏览器的默认行为造成的。 受浏览器的影响…...

深度学习 李沐报错
3.6. softmax回归的从零开始实现 — 动手学深度学习 2.0.0 documentation softmax从0开始实现 函数执行需要加main指定 改成这样 if __name__"__main__":print(evaluate_accuracy(net, test_iter)) 不然会这样出错 RuntimeError: An attempt has been m…...

【JAVA程序设计】(C00104)基于Springboot的家庭理财管理系统——有文档
基于Springboot的家庭理财管理系统项目简介项目获取开发环境项目技术运行截图运行视频项目简介 基于Springboot开发的家庭理财管理系统设计与实现共分为三个角色:系统管理员、家庭管理员、家庭用户 管理员角色包含以下功能: 用户管理、修改密码、角色管…...
【第五章 AOP概述,底层原理,AOP术语,切入点表达式,AOP操作(基于注解方式,基于xml配置文件)】
第五章 AOP概述,底层原理,AOP术语,切入点表达式,AOP操作(基于注解方式,基于xml配置文件) 1.AOP概述: (1)什么是AOP: ①面向切面编程(…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

