【面试】虚拟机栈面试题
目录
- 一、举例栈溢出的情况
- 二、调整栈大小,能保证不出现溢出吗?
- 三、分配的栈内存越大越好吗?
- 四、垃圾回收是否会涉及到虚拟机栈?
- 五、方法中定义的局部变量是否存在线程安全问题?
- 5.1 说明
- 5.2 代码示例
一、举例栈溢出的情况
- 1. 当栈的大小是固定不变的,不断调用方法,栈中不断加入栈帧,会出现栈溢出的情况StackOverflowError异常
- 2. 可以通过-Xss设置栈的大小
- 3. 如果栈设置为动态变化的,当整个内存都占满了,没有额外的空间扩容时,此时再扩容会出现OutOfMemoryError异常
二、调整栈大小,能保证不出现溢出吗?
- 1. 不能保证
- 2. 例如某个递归方法被调用1000次出现了StackOverflowError,此时调整栈大小,递归方法被调用3000次才出现异常,如果该方法正常情况下最多调用2000次,那么调整栈大小是不会出现溢出的
- 3. 如果是死循环无限递归调用方法时,无论怎么调整栈的大小,总会有溢出的时候
- 4. 调大栈的大小只能让StackOverflowError异常来得晚一些
三、分配的栈内存越大越好吗?
- 1. 理论上栈内存分配得越大,延长了出现StackOverflowError异常的时间
- 2. 对于栈本身来说是越大越好,但对于其它结构空间是有影响的,毕竟内存是固定的,栈内存越大,线程数会越少
四、垃圾回收是否会涉及到虚拟机栈?
- 1. 不会
五、方法中定义的局部变量是否存在线程安全问题?
5.1 说明
- 1. 如果只有一个线程才可以操作此数据,则是线程安全的
- 2. 如果有多个线程操作此数据,则此数据是共享数据。不考虑同步机制的话,会存在线程安全问题。
- 3. 在方法里定义的变量,且变量的生命周期仅限于该方法,则该变量是线程安全的
- 4. 如果变量是作为参数传到方法里的,或者方法中定义的变量作为返回值,给到其它方法调用,这两种情况是线程不安全的
5.2 代码示例
package com.learning.stack.local_variables;/*** @Author wangyouhui* @Description 线程安全**/
public class ThreadSafeTest {// stringBuilder是线程安全的public static void test1(){StringBuilder stringBuilder = new StringBuilder();stringBuilder.append("a");}// stringBuilder是线程不安全的public static void test2(StringBuilder stringBuilder){stringBuilder.append("a");try {Thread.sleep(100);} catch (InterruptedException e) {e.printStackTrace();}stringBuilder.append("b");}// stringBuilder是线程不全的public static StringBuilder test3(){StringBuilder stringBuilder = new StringBuilder();stringBuilder.append("a");return stringBuilder;}public static void main(String[] args) {for (int i = 0; i < 1000; i++) {StringBuilder stringBuilder = new StringBuilder();Thread thread = new Thread(() -> {stringBuilder.append("c");try {Thread.sleep(100);} catch (InterruptedException e) {e.printStackTrace();}stringBuilder.append("d");});thread.start();test2(stringBuilder);try {thread.join();} catch (InterruptedException e) {e.printStackTrace();}System.out.println(stringBuilder.toString());}}
}相关文章:

【面试】虚拟机栈面试题
目录 一、举例栈溢出的情况二、调整栈大小,能保证不出现溢出吗?三、分配的栈内存越大越好吗?四、垃圾回收是否会涉及到虚拟机栈?五、方法中定义的局部变量是否存在线程安全问题?5.1 说明5.2 代码示例 一、举例栈溢出的…...

白话熵增定律
白话熵增定律 热力学中的熵增定律 熵是指一个系统的混乱程度的度量,是热力学中的一个系统的属性。熵增定律是指一个封闭的系统随着时间的发展,在朝平衡状态发展时,其熵会增加,即其越来越混乱。 对于一个房间,如果经常…...
End-to-end people detection in crowded scenes)
(论文阅读14/100)End-to-end people detection in crowded scenes
文献阅读笔记 简介 题目 End-to-end people detection in crowded scenes 作者 Russell Stewart, Mykhaylo Andriluka 原文链接 https://arxiv.org/pdf/1506.04878.pdf 关键词 Null 研究问题 当前的人员检测器要么以滑动窗口的方式扫描图像,要么对一组离…...

Go的错误处理
什么是错误? 错误表示程序中发生的任何异常情况。假设我们正在尝试打开一个文件,但该文件在文件系统中不存在。这是一种异常情况,表示为错误。 Go 中的错误是普通的旧值。就像任何其他内置类型(例如 int、float64 等)…...

云原生相关概念
云计算 指托管在外部数据中心并按使用量付费提供给用户的软件基础设施。公司不必为昂贵的服务器付费并进行维护。相反,他们可以使用云提供商提供的按需云原生服务,例如存储、数据库和分析。 云原生 是在 云计算环境 中构建、部署和管理现代应用程序的…...
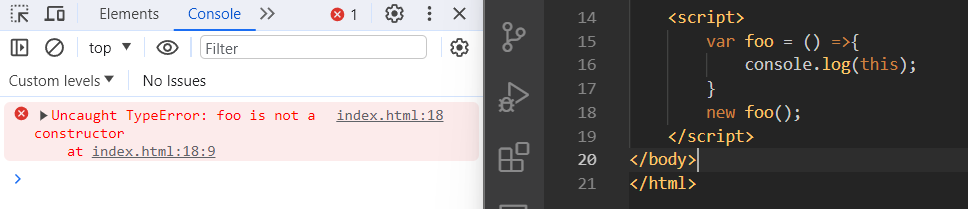
【JS】this指向
一、this指向的四种规则 1.默认绑定规则 默认指向:指向window 独立调用:指向window 对象指向,比较的是引用地址。 console.log(this window); //true console.log({} {}); //false //函数的独立调用 function test(){console.lo…...
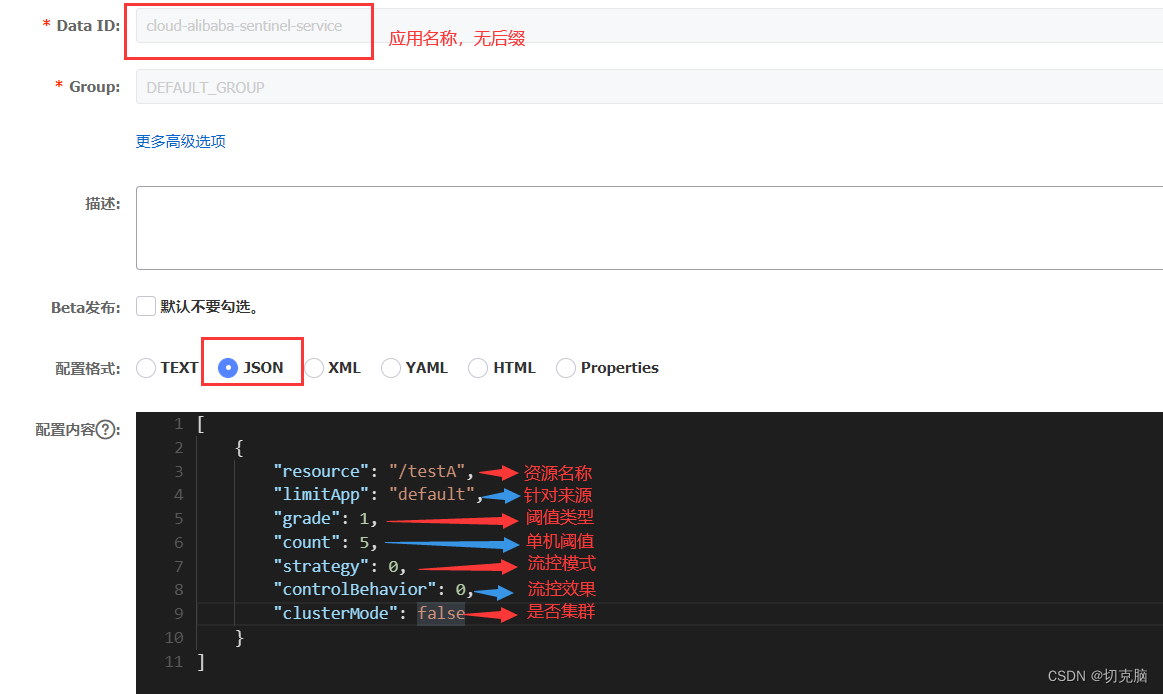
SpringCloud Alibaba Demo(Nacos,OpenFeign,Gatway,Sentinel)
开源地址: ma/springcloud-alibaba-demo 简介 参考:https://www.cnblogs.com/zys2019/p/12682628.html SpringBoot、SpringCloud 、SpringCloud Alibaba 以及各种组件存在版本对应关系。可参考下面 版本对应 项目前期准备 启动nacos. ./startup.c…...
基于nodejs+vue畅听校园点歌系统的设计与实现
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...
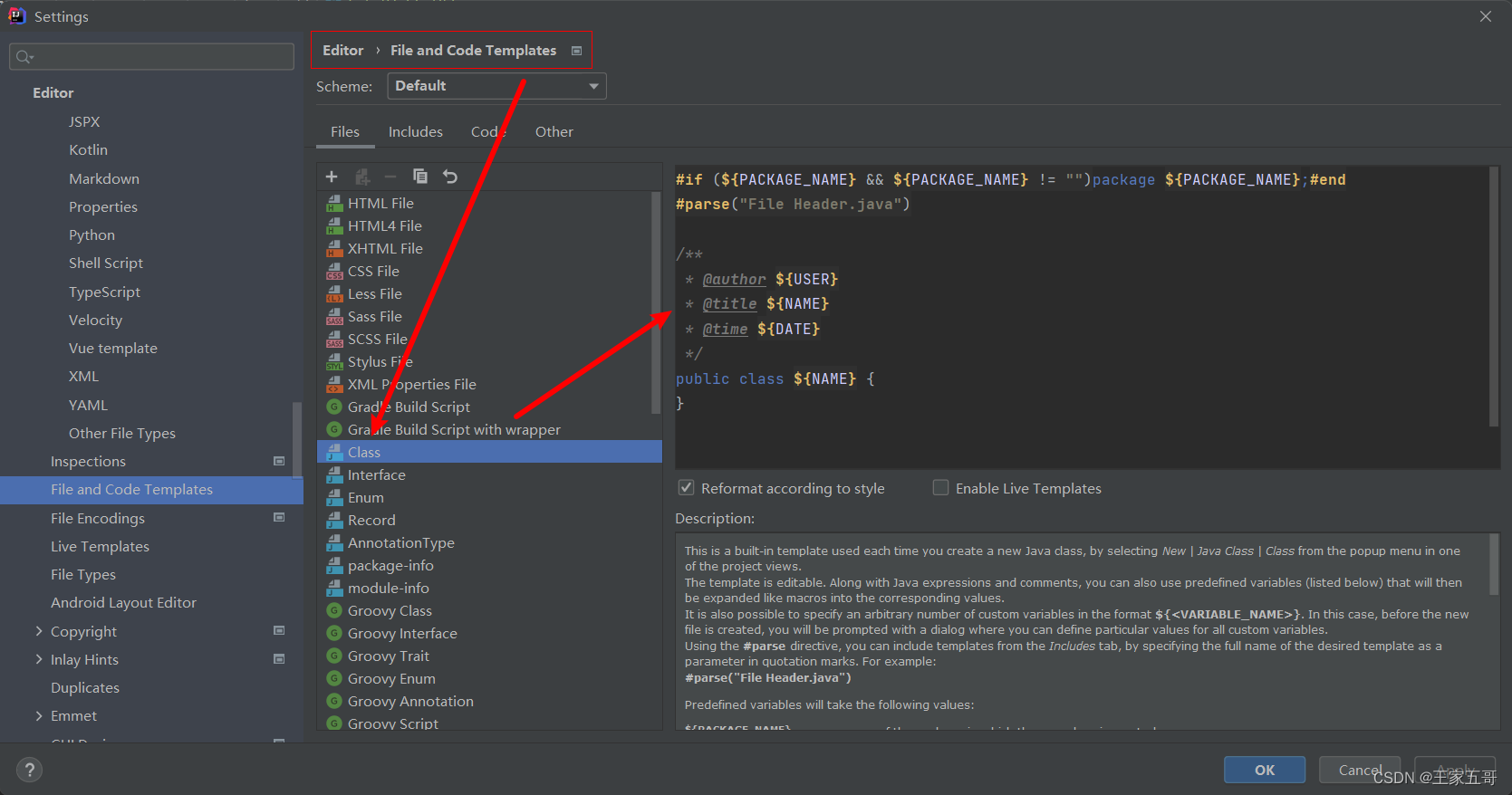
IDEA 设置代码注释模板
功能简介: 每次看别人代码时,面对毫无注释的类,除了头大还是头大, 以下提供了一种代码类注释模板 新建java类的时候,自动增加类注释,养成代码开发好习惯 效果展示: 代码模板: #if (…...

emoji对齐 特殊字符对齐 文本对齐
emoji如何对齐 特殊字符如何对齐 高级文本对齐 问题引出 我们在程序打印输出时,如何我们所输出的字符中包含emoji文本,或者其它特殊的字符文本,则我们的打印对齐效果将出现错位。以下代码复现了这一效果(tips: 马老师…...

Selenium Python 中的动作链
Selenium 是一个用于自动化的独立的基于 Web 的工具。 它是任何人都可以使用的开源工具。 与Python语言结合使用该工具进行测试。 操作链是 Selenium 的基本组成部分,提供了一种管理低级交互的方法,例如按键、鼠标移动、鼠标按钮操作以及与上下文菜单的…...
OceanBase:03-集群部署
目录 一、集群规划 二、配置要求 三、部署前配置 1.配置 limits.conf 2.配置 sysctl.conf 3.关闭防火墙 4.关闭 SELinux 5.创建数据目录,修改文件所有者信息 6.设置无密码 SSH 登录 7.安装jdk 四、解压执行安装 五、集群部署 1.OBD命令行部署 2. OBD白…...

PTA: 矩阵的乘法运算
矩阵的乘法运算 题目输入格式输出格式输入样例输出样例 代码 题目 线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时&…...
4K Video Downloader Pro v4.28.0(视频下载器)
4K Video Downloader Pro是一款专业的视频下载软件,支持从YouTube、Vimeo、Facebook、Instagram、TikTok等主流视频网站下载高质量的4K、HD和普通视频。它的操作流程简单,只需复制视频链接并粘贴到软件中即可开始下载。此外,该软件还提供了多…...

java pdf,word,ppt转图片
pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0…...
map set
目录 一、关联式容器 二、键值对 三、树形结构的关联式容器 3.1 set 3.1.1 set的介绍 3.1.2 set的使用 3.2 multiset 3.2.1 multiset的介绍 3.2.2 multiset的使用 3.3 map 3.3.1 map的介绍 3.3.2 map的使用 …...
Fourier分析导论——第3章——Fourier级数的收敛性(E.M. Stein R. Shakarchi)
第 3 章 Fourier级数的收敛性(Convergence of Fourier Series) The sine and cosine series, by which one can represent an arbitrary function in a given interval, enjoy among other remarkable properties that of being convergent. This property did not escape…...
解决ruoyi-vue部署到域名子路径静态资源404
参考ruoyi前端手册...

游戏引擎中为什么要用四元数表示旋转而不用欧拉角旋转?
个人观点,仅供参考,如有错误可太刺激了 四元数的简单概念和使用 欧拉角通常用于表示一个物体的旋转状态,而不是表示旋转过程。 欧拉角描述的是物体相对于某个参考坐标系的朝向或旋转状态,通常以不同的轴(例如&#x…...
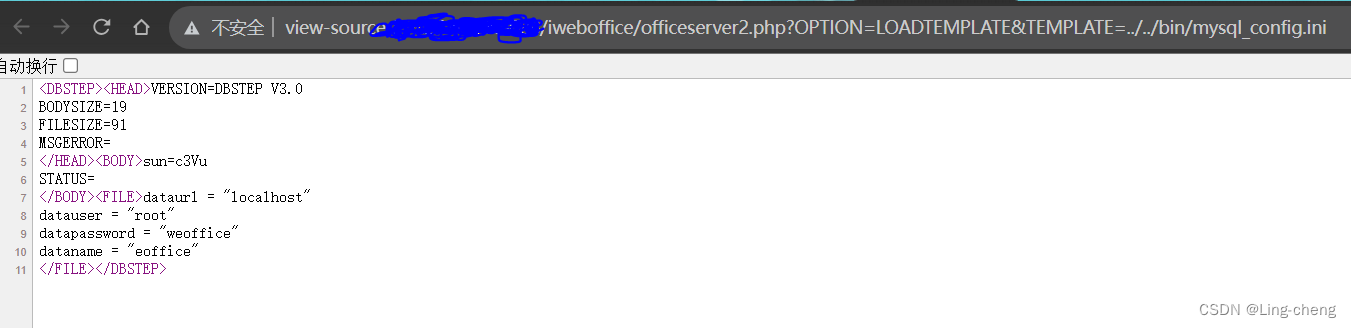
E-Office(泛微OA)前台任意文件读取漏洞复现
简介 泛微E-Office是一款企业级的全流程办公自动化软件,它包括协同办公、文档管理、知识管理、工作流管理等多个模块,涵盖了企业日常工作中的各个环节。在该产品前台登录页存在文件读取漏洞。 officeserver.php文件存在任意文件读取漏洞,通…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
