C++二叉搜索树
本章主要是二叉树的进阶部分,学习搜索二叉树可以更好理解后面的map和set的特性。
1.二叉搜索树概念
二叉搜索树的递归定义为:非空左子树所有元素都小于根节点的值,非空右子树所有元素都大于根节点的值,而左右子树也是二叉搜索树。
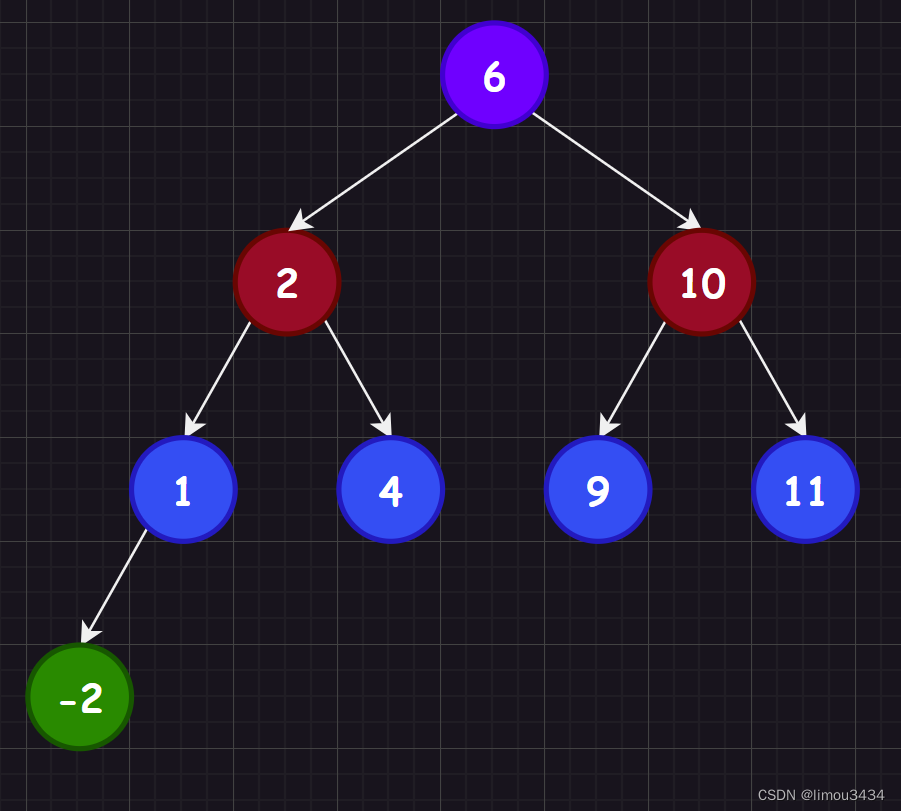
2.二叉搜索树实现
2.1.接口分析
2.1.1.查找
- 从根开始比较查找,比根大则往右边走查找,比根小则往左边走查找。
- 最多查找高度次,走到空,还没找到,则该值不存在。
2.1.2.插入
- 树为空,则直接新增节点,赋值给
root指针 - 树不空,按二叉搜索树性质查找插入位置,插入新节点
2.1.3.删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回false。否则要删除的结点可能分下面四种情况:
- 要删除的结点无孩子结点
- 要删除的结点只有左孩子结点
- 要删除的结点只有右孩子结点
- 要删除的结点有左、右孩子结点
看起来有待删除节点有四种情况,实际情况1可以与情况2或者3合并起来,因此真正的删除过程如下:
-
情况
1:删除该结点且使被删除节点的双亲结点指向被删除结点的左/右孩子结点(直接删除)) -
情况
2:在它的右子树中寻找中序下的第一个结点(关键码最小,也就是右子树中最小的结点),用它的值填补到被删除节点中,再来处理该结点的删除问题(替换法删除)补充:实际上情况
2找左子树的最大节点也是可以的。
上述体现了一种“托孤”的现象,这和Linux中孤儿进程的托孤很是类似。
2.2.具体实现
#include <iostream>
#include <string>
using namespace std;template<typename K>//这里更加习惯写K,也就是关键值key的类型
struct BinarySearchTreeNode
{BinarySearchTreeNode<K>* _left;BinarySearchTreeNode<K>* _right;K _key; BinarySearchTreeNode(K key = K()) : _key(key), _left(nullptr), _right(nullptr) {}
};template<typename K>
class BinarySearchTree
{typedef BinarySearchTreeNode<K> Node;
public://BinarySearchTree() : _root(nullptr) {}BinarySearchTree() = default;//强制编译器生成默认的构造函数BinarySearchTree(const BinarySearchTree<K>& b){_root = copy(b._root);}BinarySearchTree<K>& operator=(BinarySearchTree<K> b)//b拷贝了一份{swap(_root, b._root);return *this;}~BinarySearchTree(){destroy(_root);}//1.插入bool insert(const K& key){/*对于第一个插入的节点就是根节点。至于数据冗余,我在这里定义不允许数据冗余,也就是不允许出现重复的数据节点。这样的搜索二叉树会受到数据先后顺序插入的影响(您也可定义允许)*///1.查看是否根节点if (_root == nullptr){_root = new Node(key);return true;}//2.寻找存放的位置Node* parent = nullptr;//存放root的父节点Node* root = _root;//遍历,从根节点开始while (root)//直到空为止{parent = root;if (root->_key < key) {root = root->_right;}else if(root->_key > key){root = root->_left;}else//root->_key == key{return false;//默认不允许重复数据}}//3.插入节点及数据root = new Node(key);if (parent->_key < key)//注意不可以直接赋值给root,不仅内存泄露还连接不上节点{parent->_right = root;}else{parent->_left = root;}return true;}bool insertR(const K& key){return _insertR(_root, key);}//2.删除bool erase(const K& key){/*寻找被删除的节点,删除后,如果是单子节点还好,如果是多子节点就需要找到一个托孤后依旧满足二叉搜索树性质的节点,因此删除有两种情况:A.被删除节点是叶子节点 或者 被删除节点的左或右孩子为空,直接将孩子节点替换被删除节点即可B.被删除节点拥有两个子节点,取右子树中最小的节点替代被删除的节点(当然也可以取左子树的最大节点)b1.最小节点没有右孩子,最小节点直接替代被删除节点,并且将最小节点的空孩子节点交给父节点领养b2.最小节点存在右孩子,最小节点直接替代被删除节点,并且将最小节点的右孩子节点交给父节点领养最后还需要注意删除根节点,根节点没有父节点的问题*/Node* parent = nullptr;Node* cur = _root;//1.寻找节点while (cur){if (cur->_key < key){parent = cur;//不可以和下一个if语句共用,会出现cur和parenat的情况,例如:test_1()中删除10的时候cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//2.删除节点(找到了)if (cur->_left == nullptr)//2.1.左为空{if (parent == nullptr)//避免cur是根节点,没有父节点,例如:test_1()中删除11的时候{_root = cur->_right;delete cur;return true;}if (parent->_left == cur){parent->_left = cur->_right;}else//parent->_right == cur{parent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//2.2.右为空{if (parent == nullptr){_root = cur->_left;delete cur;return true;}if (parent->_left == cur){parent->_left = cur->_left;}else//parent->_right == cur{parent->_right = cur->_left;}delete cur;}else//2.3.左右均不为空,取左子树中最大的或者取右子树中最小的节点替代被删除的节点{Node* pminRight = cur;//注意不能为nullptr,因为有可能出现不进循环的情况Node* minRight = cur->_right;//我们选择找右数最小节点while (minRight->_left != nullptr)//找到最左节点,但是需要注意这个最左节点如果有右树,那就需要最左节点的父节点接管{pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//替换相当于删除if (pminRight->_left == minRight)//最左节点的父节点托管最左节点的右树,注意可能有两种情况{pminRight->_left = minRight->_right;}else if (pminRight->_right == minRight)//最左节点的父节点托管最左节点的右树,注意可能有两种情况{pminRight->_right = minRight->_right;}delete minRight;}return true;}}return false;}bool eraseR(const K& key){return _eraseR(_root, key);}//3.查找bool find(const K& key){Node* root = _root;while (root){if (root->_key < key){root = root->_right;}else if (root->_key > key){root = root->_left;}else{return true;}}return false;}bool findR(const K& key){return _findR(_root, key);}//4.打印void inOrder(){_inOrder(_root);cout << endl;}private://1.销毁(提供给析构)void destroy(Node*& root){if (root == nullptr)return;destroy(root->_left);destroy(root->_right);delete root;root = nullptr;}//2.拷贝(提供给拷贝构造)Node* copy(Node* root){if (root == nullptr){return nullptr;}Node* newroot = new Node(root->_key);newroot->_left = copy(root->_left);newroot->_right = copy(root->_right);return newroot;}//3.插入(提供给递归插入)bool _insertR(Node*& root, const K& key)//注意root是引用{if (root == nullptr){root = new Node(key);//这里由于传递的是引用,那么root就是上一级递归的root->_left或者root->_rightreturn true;}if (root->_key < key){return _insertR(root->_right, key);}else if (root->_key > key){return _insertR(root->_left, key);}else{return false;}}//4.删除(提供给递归插入)bool _eraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _eraseR(root->_right, key);}else if (root->_key > key){return _eraseR(root->_left, key);}else//root->_key == key{Node* del = root;//保存要删除的节点if (root->_right == nullptr){root = root->_left;}else if (root->_left == nullptr){root = root->_right;}else//左右均不为空{Node* maxleft = root->_left;while (maxleft->_right != nullptr)//找左树的最大节点{maxleft = maxleft->_right;}swap(root->_key, maxleft->_key);return _eraseR(root->_left, key);//由于左树的最大节点必有一个空孩子节点,因此使用递归删除即可,可以看到递归的删除比非递归及其的简单明了(注意不可以直接传递maxleft,这是一个局部变量)}delete del;return true;}}//5.查找(提供给递归查找)bool _findR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key < key){return _isRecursionFind(root->_left, key);}else//root->_key > key{return _isRecursionFind(root->_right, key);}}//6.打印(提供给递归打印)void _inOrder(Node* root)//注意这里不能直接就拿_root当作缺省值了,因为缺省值只能是常量或者全局变量,而_root需要使用this->_root,而this指针是函数形参,不一定传过来了,别谈使用_root了{if (root == nullptr)return;_inOrder(root->_left);cout << root->_key << " ";_inOrder(root->_right);}//?.成员变量Node* _root;
};
这里我还为您提供了三个测试样例:
//普通测试
void test_1()
{BinarySearchTree<int> b;b.insert(6);b.insert(2);b.insert(1);b.insert(4);b.insert(-2);b.insert(10);b.insert(9);b.insert(11);b.inOrder();b.erase(6);b.inOrder();b.erase(2);b.inOrder();b.erase(10);b.inOrder();b.erase(1);b.inOrder();b.erase(4);b.inOrder();b.erase(9);b.inOrder();b.erase(11);b.inOrder();b.erase(-2);b.inOrder();
}
//头删测试(需要该_root为公有成员才可以测试)
void test_2()
{BinarySearchTree<int> b;b.insert(6);b.insert(2);b.insert(1);b.insert(4);b.insert(-2);b.insert(10);b.insert(9);b.insert(11);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();//b.erase(b._root->_key);//b.inOrder();
}
//递归测试
void test_3()
{BinarySearchTree<int> b;b.insertR(6);b.insertR(2);b.insertR(1);b.insertR(4);b.insertR(-2);b.insertR(10);b.insertR(9);b.insertR(11);BinarySearchTree<int> b1(b);b.inOrder();b.eraseR(6);b.inOrder();b.eraseR(2);b.inOrder();b.eraseR(10);b.inOrder();b.eraseR(1);b.inOrder();b.eraseR(4);b.inOrder();b.eraseR(9);b.inOrder();b.eraseR(11);b.inOrder();b.eraseR(-2);b.inOrder();b1.inOrder();b.inOrder();
}
3.二叉搜索树应用
3.1.Key模型
考虑“在不在”的问题,例如:
- 门禁系统
- 车库系统
- 单词检查、搜索…
查找对象是否在数据库中存在,这样的场景在现实中有很多。
3.2.Key/Value模型
通过一个值查找另外一个值,例如:
- 中英文互译
- 电话号码查询快递信息
- 验证码查询信息…
只需要在一个节点中包含一个数据对即可。
另外我们之前说过二叉搜索树一般不存储重复的元素,如果相同的元素可以让该元素绑定一个int元素形成键值对,这种情况的实际应用有:统计高频词汇。
补充:实际上,上面的这两种模型对标的是
C++的set和map容器,这些我们后续学习。
4.二叉搜索树分析
由于缺失平衡性,二叉搜索树在最不理想的状态(一颗斜树)查找的时间复杂度是 O ( n ) O(n) O(n),最好的效率是 O ( l o g 2 ( N ) ) O(log_{2}(N)) O(log2(N))。
相关文章:

C++二叉搜索树
本章主要是二叉树的进阶部分,学习搜索二叉树可以更好理解后面的map和set的特性。 1.二叉搜索树概念 二叉搜索树的递归定义为:非空左子树所有元素都小于根节点的值,非空右子树所有元素都大于根节点的值,而左右子树也是二叉搜索树…...
elasticsearch索引按日期拆分
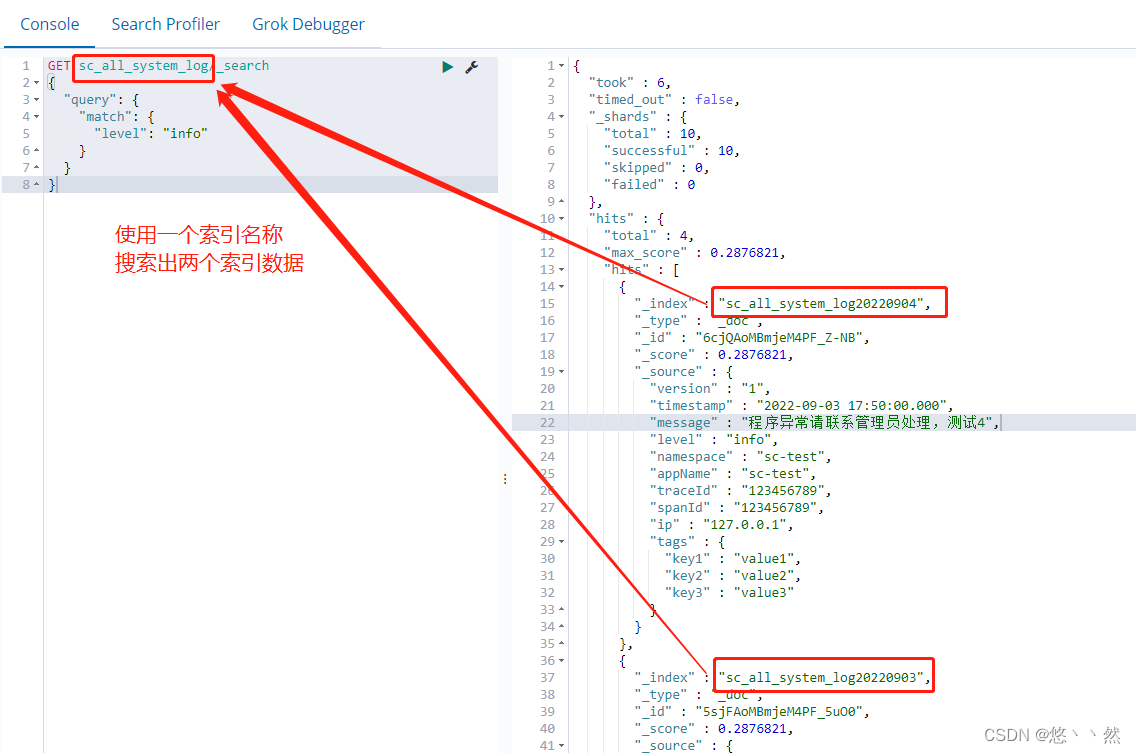
1.索引拆分原因 如果单个索引数据量过大会导致搜索变慢,而且不方便清理历史数据。 例如日志数据每天量很大,而且需要定期清理以往日志数据。例如原索引为sc_all_system_log,现按天拆分索引sc_all_system_log20220902,sc_all_syste…...

纯python实现大漠图色功能
大漠图色是一种自动化测试工具,可以用于识别屏幕上的图像并执行相应的操作。在Python中,可以使用第三方库pyautogui来实现大漠图色功能。具体步骤如下: 安装pyautogui库:在命令行中输入pip install pyautogui。导入pyautogui库&a…...

debounce and throtlle
debounce // 核心:单位时间内触发>1 则只执行最后一次。//excutioner 可以认为是执行器。执行器存在则清空,再赋值新的执行器。function debounce(fn, delay 500) {let excutioner null;return function () {let context this;let args arguments…...

四、数据库系统
数据库系统(Database System),是由数据库及其管理软件组成的系统。数据库系统是为适应数据处理的需要而发展起来的一种较为理想的数据处理系统,也是一个为实际可运行的存储、维护和应用系统提供数据的软件系统,是存储介…...
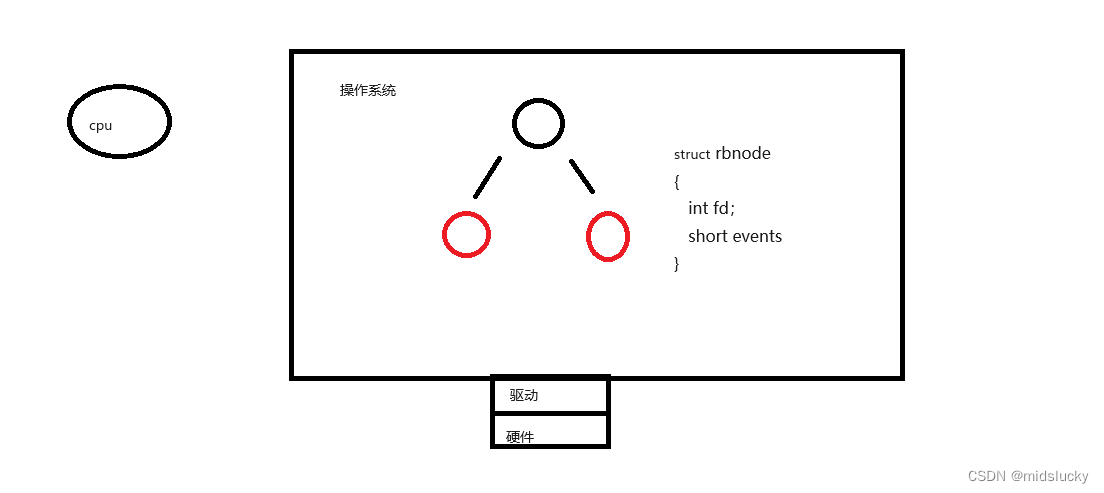
Linux中的高级IO
文章目录 1.IO1.1基本介绍1.2基础io的低效性1.3如何提高IO效率1.4五种IO模型1.5非阻塞模式的设置 2.IO多路转接之Select2.1函数的基本了解2.2fd_set理解2.3完整例子代码(会在代码中进行讲解)2.4优缺点 3.多路转接之poll3.1poll函数的介绍3.2poll服务器3.…...
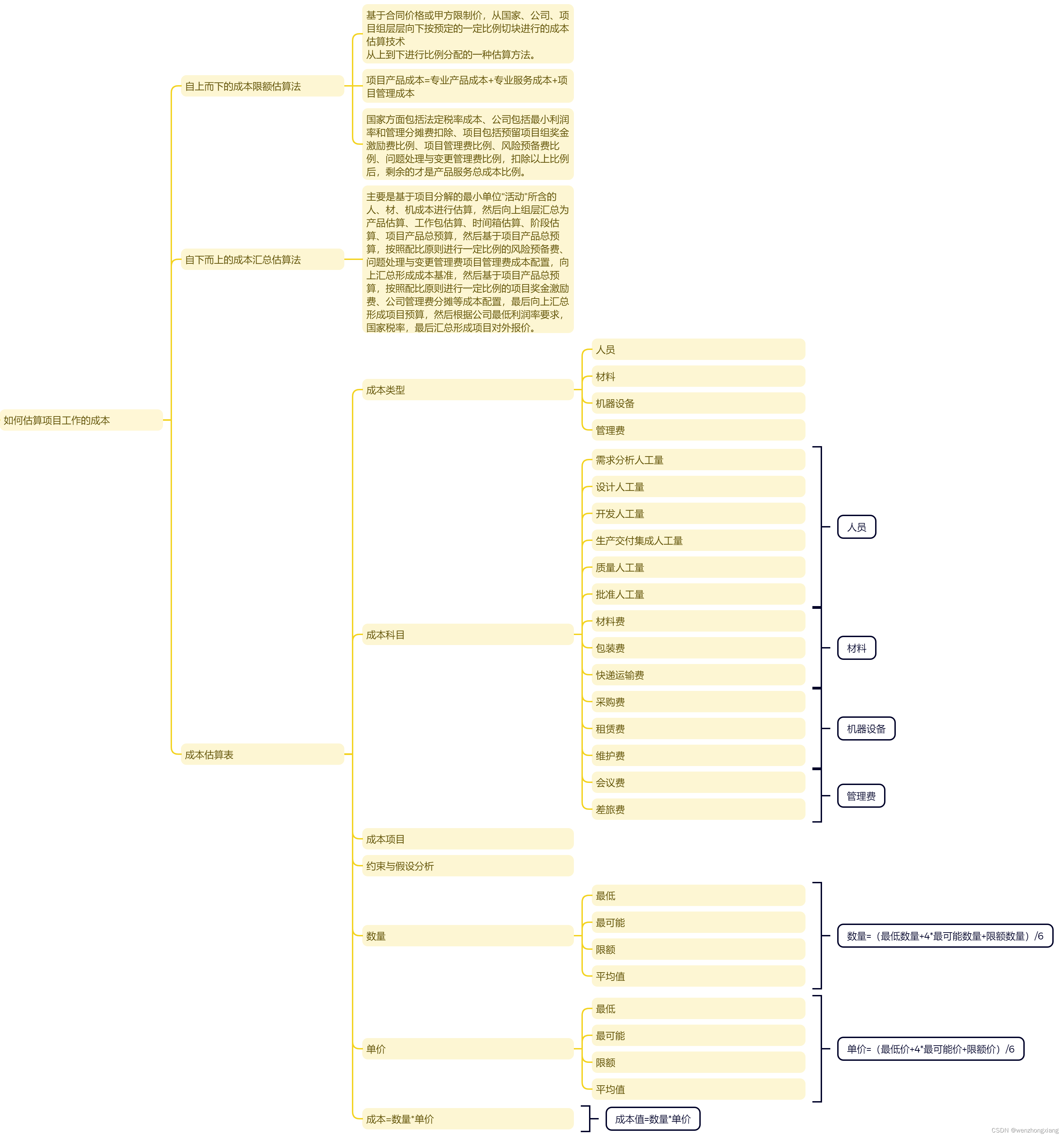
项目管理之如何估算项目工作成本
在项目管理中,如何估算项目工作成本是一个关键问题。为了解决这个问题,我们可以采用自上而下的成本限额估算法和自下而上的成本汇总估算法。这两种方法各有优缺点,但都可以帮助我们准确地估算项目工作成本。 自上而下的成本限额估算法 自上…...

Redis主从复制基础概念
Redis主从复制:提高数据可用性和性能的策略 一、概述 Redis主从复制是一种常用的高可用性策略,通过将数据从一个Redis服务器复制到另一个或多个Redis服务器上,以提高数据的可用性和读取性能。当主服务器出现故障时,可以快速地切…...
图数据库Neo4j概念、应用场景、安装及CQL的使用
一、图数据库概念 引用Seth Godin的说法,企业需要摒弃仅仅收集数据点的做法,开始着手建立数据之间的关联关系。数据点之间的关系甚至比单个点本身更为重要。 传统的**关系数据库管理系统(RDBMS)**并不擅长处理数据之间的关系,那些表状数据模…...
: RIP原理与配置)
路由器基础(四): RIP原理与配置
路由信息协议 (Routing Information Protocol,RIP) 是最早使用的距离矢量路由协议。因为路由是以矢量(距离、方向)的方式被通告出去的,这里的距离是根据度量来决定的,所以叫“距离矢量”。 距离矢量路由算法是动态路由算法。它的工作流程是:…...

红外遥控开发RK3568-PWM-IR
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言1.红外遥控的发送接收工作原理2.红外协议3.红外遥控系统框图4.遥控器添加方法4.1 记录键值4.2 添加键值总结前言 提示:这里可以添加本文要记录的大概内容: 1.红外遥控的发送接收工作原理 …...

go-sync-mutex
Sync Go 语言作为一个原生支持用户态进程(Goroutine)的语言,当提到并发编程、多线程编程时,往往都离不开锁这一概念。锁是一种并发编程中的同步原语(Synchronization Primitives),它能保证多…...
高并发系统设计
高并发系统通用设计方法 Scala-out 横向扩展,分散流量,分布式集群部署 缺点:引入复杂度,节点之间状态维护,节点扩展(上下线) Scala-up 提升单机性能,比如增加内存,增…...

Vue3-Pinia快速入门
1.安装pinia npm install pinia -save 2.在main.js中导入并使用pinia // 导入piniaimport { createPinia } from "pinia"; const pinia createPinia();//使用pinia app.use(pinia)app.mount(#app) 3.在src目录下创建包:store,表示仓库 4…...

Python算法——插入排序
插入排序(Insertion Sort)是一种简单但有效的排序算法,它的基本思想是将数组分成已排序和未排序两部分,然后逐一将未排序部分的元素插入到已排序部分的正确位置。插入排序通常比冒泡排序和选择排序更高效,特别适用于对…...

Java21新特性
目录 一、Java21新特性 1、字符串模版 2、scoped values 3、record pattern 4、switch格式匹配 5、可以在switch中使用when 6、Unnamed Classes and Instance Main Methods 7、Structured Concurrency 一、Java21新特性 1、字符串模版 字符串模版可以让开发者更简洁的…...
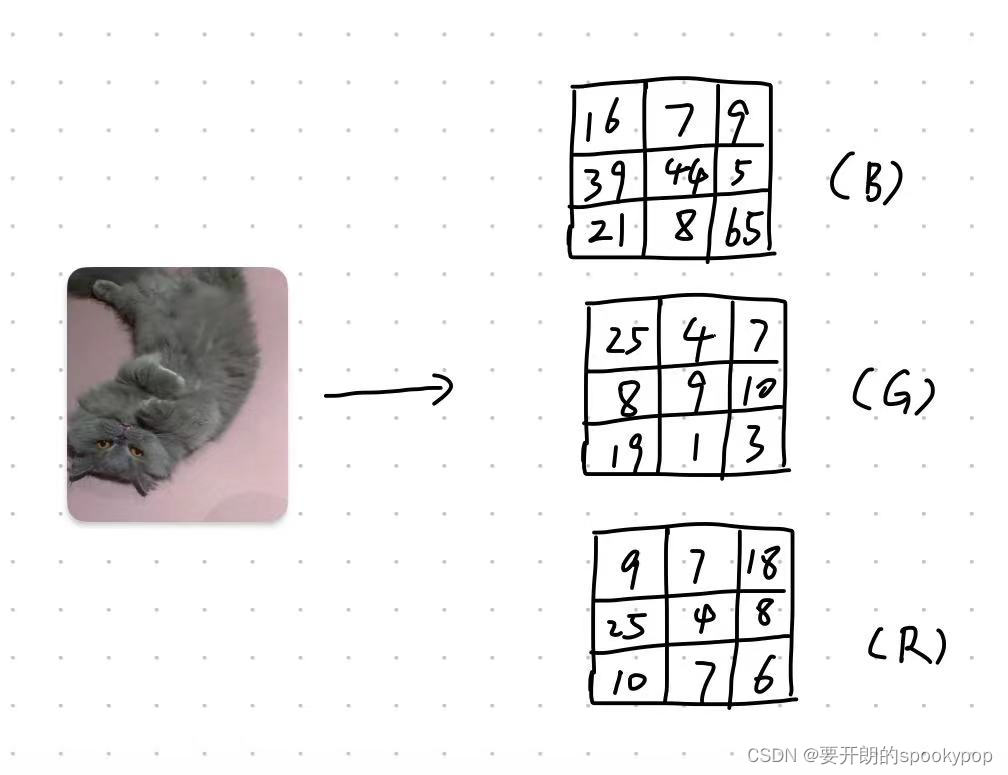
4 Tensorflow图像识别模型——数据预处理
上一篇:3 tensorflow构建模型详解-CSDN博客 本篇开始介绍识别猫狗图片的模型,内容较多,会分为多个章节介绍。模型构建还是和之前一样的流程: 数据集准备数据预处理创建模型设置损失函数和优化器训练模型 本篇先介绍数据集准备&am…...
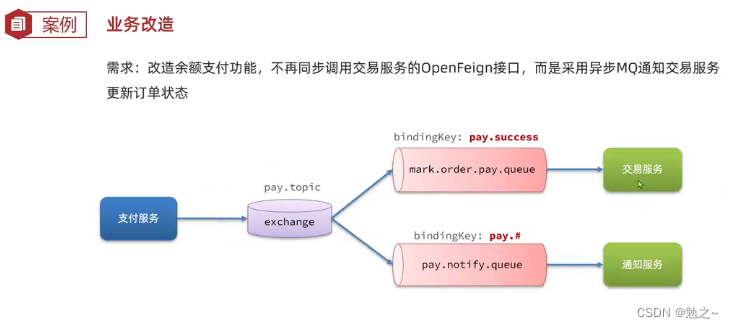
SpringBoot整合RabbitMQ学习笔记
SpringBoot整合RabbitMQ学习笔记 以下三种类型的消息,生产者和消费者需各自启动一个服务,模拟生产者服务发送消息,消费者服务监听消息,分布式开发。 一 Fanout类型信息 . RabbitMQ创建交换机和队列 在RabbitMQ控制台,新…...

在校园跑腿系统小程序中,如何设计高效的实时通知与消息推送系统?
1. 选择合适的消息推送服务 在校园跑腿系统小程序中,选择一个适合的消息推送服务。例如,使用WebSocket技术、Firebase Cloud Messaging (FCM)、或第三方推送服务如Pusher或OneSignal等。注册并获取相关的API密钥或访问令牌。 2. 集成服务到小程序后端…...

求极限Lim x->0 (x-sinx)*e-²x / (1-x)⅓
题目如下: 解题思路: 这题运用了无穷小替换、洛必达法则、求导法则 具体解题思路如下: 1、首先带入x趋近于0,可以得到(0*1)/0,所以可以把e的-x的平方沈略掉 然后根据无穷小替换,利用t趋近于0时…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
