容斥恒等式的证明
容斥恒等式的证明
推广公式
P(A∪B)=P(A)+P(B)−P(A∩B)P(A\cup B)=P(A)+P(B)-P(A\cap B) P(A∪B)=P(A)+P(B)−P(A∩B)
(a)设A、B、C为三个事件,则下列恒等式成立:
P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)P(A\cup B\cup C)=P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C) P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
(b)设A1A_1A1,A2A_2A2,A3A_3A3,…,AnA_nAn为n个事件,令S1S_1S1={i∣1≤i≤ni|1\leq i \leq ni∣1≤i≤n},S2S_2S2={(i1,i2)∣1≤i1<i2≤n(i_1,i_2)|1\leq i_1 < i_2 \leq n(i1,i2)∣1≤i1<i2≤n},一般的,令S1S_1S1为满足条件$ \le i_1 < i_2<… < i_m\le n的m维指标,(的m维指标,(的m维指标,(i_1,…i_m$)的集合,则下列恒等式成立:
P(∪k=1nAk)=∑i∈S1P(Ai)−∑(i1,i2)∈S2P(Ai1∩Ai2)+∑i1,i2,i3∈S3P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)P(\cup^n_{k=1}A_k)=\displaystyle \sum_{i\in S_1}P(A_i)-\displaystyle\sum_{(i_1,i_2)\in S_2}P(A_{i_1} \cap A_{i_2})+\displaystyle \sum_{i_1,i_2,i_3 \in S_3}P(A_{i_1} \cap A_{i_2} \cap A_{i_3})-...+(-1)^{n-1}P(\cap^n_{k=1}A_{k})P(∪k=1nAk)=i∈S1∑P(Ai)−(i1,i2)∈S2∑P(Ai1∩Ai2)+i1,i2,i3∈S3∑P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)
解:(a)利用公式P(X∪Y)=P(X)+P(Y)−P(X∩Y)P(X\cup Y)=P(X)+P(Y)-P(X\cap Y)P(X∪Y)=P(X)+P(Y)−P(X∩Y)和(A∪B)∩C=(A∩C)∪(B∩C)(A\cup B)\cap C=(A\cap C)\cup (B\cap C)(A∪B)∩C=(A∩C)∪(B∩C),我们有
P(A∪B∪C)=P(A∪B)+P(C)−P((A∪B)∩C)=P(A∪B)+P(C)−P((A∩C)∪(B∩C))=P(A∪B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C)=P(A)+P(B)−P(A∩B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)P(A\cup B\cup C)=P(A\cup B)+P(C)-P((A\cup B )\cap C) \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A\cup B)+P(C)-P((A\cap C )\cup (B\cap C))\\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A\cup B)+P(C)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C) \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A)+P(B)-P(A\cap B)+P(C)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C) \\~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ =P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C)+P(A\cap B\cap C)P(A∪B∪C)=P(A∪B)+P(C)−P((A∪B)∩C) =P(A∪B)+P(C)−P((A∩C)∪(B∩C)) =P(A∪B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C) =P(A)+P(B)−P(A∩B)+P(C)−P(A∩C)−P(B∩C)+P(A∩B∩C) =P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
(b)利用归纳法,主要推断部分可以模仿(a)中步骤
n=2时,P(A∪B)=P(A)+P(B)−P(A∩B)P(A\cup B)=P(A)+P(B)-P(A\cap B)P(A∪B)=P(A)+P(B)−P(A∩B).
假设n=k-1,有
P(∪k=1k−1Ak)=∑i∈S1P(Ai)−∑(i1,i2)∈S2P(Ai1∩Ai2)+∑i1,i2,i3∈S3P(Ai1∩Ai2∩Ai3)−...+(−1)n−2P(∩k=1k−1Aik)P(\cup^{k-1}_{k=1}A_k)=\displaystyle \sum_{i\in S_1}P(A_i)-\displaystyle\sum_{(i_1,i_2)\in S_2}P(A_{i_1} \cap A_{i_2})+\displaystyle \sum_{i_1,i_2,i_3 \in S_3}P(A_{i_1} \cap A_{i_2} \cap A_{i_3})-...+(-1)^{n-2}P(\cap^{k-1}_{k=1}A_{i_k})P(∪k=1k−1Ak)=i∈S1∑P(Ai)−(i1,i2)∈S2∑P(Ai1∩Ai2)+i1,i2,i3∈S3∑P(Ai1∩Ai2∩Ai3)−...+(−1)n−2P(∩k=1k−1Aik)
则n=k时,P(∪k=1nAk)=P(∪k=1k−1Ak∪Ak)P(\cup^n_{k=1}A_k)=P(\cup^{k-1}_{k=1}A_k\cup A_k)P(∪k=1nAk)=P(∪k=1k−1Ak∪Ak)
令∪i=1k−1Ai=B\cup^{k-1}_{i=1}A_i=B∪i=1k−1Ai=B,
P(∪k=1nAk)=P(B∪Ak)P(\cup^n_{k=1}A_k)=P(B\cup A_k)P(∪k=1nAk)=P(B∪Ak)
所以,
P(∪k=1nAk)=P(B∪Ak)=P(B)+P(Ak)−P(B∩Ak)P(\cup^n_{k=1}A_k)=P(B\cup A_k)=P(B)+P(A_k)-P(B\cap A_k)P(∪k=1nAk)=P(B∪Ak)=P(B)+P(Ak)−P(B∩Ak) (1)
前两个地方都很好推导,主要是最后一项。
P(B∩Ak)=P(∪i=1k−1AiAk)=∑i=1k−1P(AiAk)+(−11)∑1≤i1<i2≤ik−1P(Ai1Ai2Ak)+...+(−1)k−2P(A1A2...Ak)P(B\cap A_k)=P(\cup^{k-1}_{i=1}A_iA_k)\\=\displaystyle \sum_{i=1}^{k-1}P(A_iA_k)+(-1^1) \displaystyle \sum_{1\le i_1<i_2\le i_{k-1}}P(A_{i_1}A_{i_2}A_k)+...+(-1)^{k-2}P(A_1A_2...A_k)P(B∩Ak)=P(∪i=1k−1AiAk)=i=1∑k−1P(AiAk)+(−11)1≤i1<i2≤ik−1∑P(Ai1Ai2Ak)+...+(−1)k−2P(A1A2...Ak) (2)
把(2)带入(1),
得到:
P(∪k=1nAk)=∑i∈S1P(Ai)−∑(i1,i2)∈S2P(Ai1∩Ai2)+∑i1,i2,i3∈S3P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)P(\cup^n_{k=1}A_k)=\displaystyle \sum_{i\in S_1}P(A_i)-\displaystyle\sum_{(i_1,i_2)\in S_2}P(A_{i_1} \cap A_{i_2})+\displaystyle \sum_{i_1,i_2,i_3 \in S_3}P(A_{i_1} \cap A_{i_2} \cap A_{i_3})-...+(-1)^{n-1}P(\cap^n_{k=1}A_{k})P(∪k=1nAk)=i∈S1∑P(Ai)−(i1,i2)∈S2∑P(Ai1∩Ai2)+i1,i2,i3∈S3∑P(Ai1∩Ai2∩Ai3)−...+(−1)n−1P(∩k=1nAk)
得证。
相关文章:

容斥恒等式的证明
容斥恒等式的证明 推广公式 P(A∪B)P(A)P(B)−P(A∩B)P(A\cup B)P(A)P(B)-P(A\cap B) P(A∪B)P(A)P(B)−P(A∩B) (a)设A、B、C为三个事件,则下列恒等式成立: P(A∪B∪C)P(A)P(B)P(C)−P(A∩B)−P(A∩C)−P(B∩C)P(A∩B∩C)P(A\cup B\cup C)P(A)P(B)P(C)…...

Java中的this与super关键字深度解析
一、this关键字this 关键字是 Java 常用的关键字,可用于任何实例方法内指向当前对象,也可指向对其调用当前方法的对象,或者在需要当前类型对象引用时使用。(1)this.属性名this修饰的变量用于指代成员变量方法的形参如果…...

CSS3新增的视口单位Vh、Vw单位
定义vw:浏览器可见视口【宽度】的百分比(1vw代表视窗【宽度】的1%)vh:浏览器可见视口【高度】的百分比(1vw代表视窗【高度】的1%)vmin:当前 vw 和 vh 较小的一个值。vmax:当前 vw 和…...
【Linux】yum安装docker指定版本
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录卸载已有的docker部署指定版本docker安…...
SpringBoot相关操作
01-今日内容 Spring概述、快速入门SpringBoot配置SpringBoot整合 02-SpringBoot概述 SpringBoot提供了一种快速使用Spring的方式,基于约定优于配置的思想,可以让开发人员不必在配置与逻辑业务之间进行思维的切换,全身心的投入到逻辑业务的…...
函数:调用父类的构造方法)
Python super()函数:调用父类的构造方法
Python 中子类会继承父类所有的类属性和类方法。严格来说,类的构造方法其实就是实例方法,因此毫无疑问,父类的构造方法,子类同样会继承。 但我们知道,Python 是一门支持多继承的面向对象编程语言,如果子类…...
@ConfigurationProperties在方法上的使用
文章目录1. 前言2. 先说结论3. 代码解释1. Component ConfigurationProperties2. EnableConfigurationProperties ConfigurationProperties3. Bean ConfigurationProperties1. 前言 在学习spring的时候,ConfigurationProperties应该经常被使用到,作用…...
)
【QT】如何查找和获取界面上的子部件(findChild 和 findChidren)
目录1. findChild()函数2. findChildren()函数3. 示例1. findChild()函数 函数原型: T QObject::findChild(const QString &name QString(), Qt::FindChildOptions options Qt::FindChildrenRecursively) const返回该对象的子对象,该子对象可以转…...

MIT 6.S081学习笔记
计划花25天时间学完6.S081课程,从2月20日-3月20日。课程主页Link xv6 book GDB User Manual Lecture 1: Introduction and Examples课程主题:设计和实现操作系统 OS的三大功能:多路复用、隔离和交互。 Lab: Xv6 and Unix utiliti…...
《网络安全入门到精通》 - 2.1 - Windows基础 - DOS命令Windows防火墙Windows共享文件
「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「订阅专栏」:此文章已录入专栏《网络安全入门到精通》 Windows基础一、DOS命令1、目录文件操作dir 列出目录文件cd 切换目录md 创建目录rd 删除目录move 移动文件或目…...
八、Vben框架动态生成可编辑Table
开发过程中产品经理提出了一些奇怪的需求,让人很摸不着头脑,一问就是客户的需求就是这样,那么我们开发只能想各种办法啦。 最近就提出了两个需求, 第一个是需要在日期选择的时候根据时间选择的不同让底下table中增加两个时间中间的…...

浅谈ERP数据的重要性
影响一个ERP项目的因素有很多,数据无疑是其中很重要的一项,正所谓“正确的诊断源于准确的信息,准确的信息基于可靠的采集”,当我们抓住数据这个根基,大处着眼,小处着手的时候,我们距离ERP成功的日子就不会太…...

【RabbitMQ笔记06】消息队列RabbitMQ七种模式之Topics主题模式
这篇文章,主要介绍消息队列RabbitMQ七种模式之Topics主题模式。 目录 一、消息队列 1.1、主题模式(Topics) 1.2、案例代码 (1)引入依赖 (2)编写生产者 (3)编写消费…...

ChatGPT似乎有的时候并不能搞懂Java的动态分派,你懂了吗?
目录 碎碎念 ChatGPT 中出现的问题 那么正确答案应该是什么呢? 分派的相关知识点总结: 分派是什么? 静态分派与动态分派: Java语言是静态多分派,动态单分派的; 静态分派:静态重载多分派…...
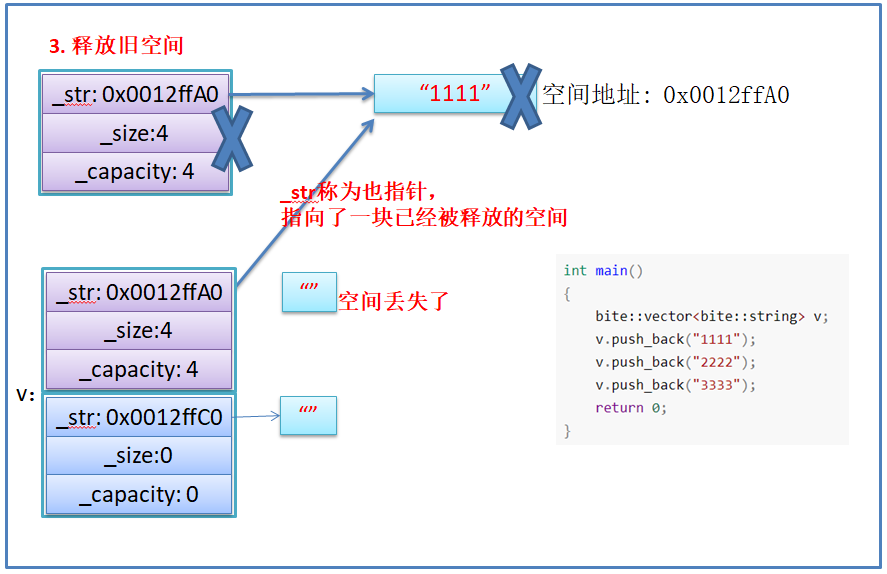
【C++初阶】vector的模拟实现
大家好我是沐曦希💕 文章目录一、前言二、无参构造&析构三、基础接口1.empty和clear2.size和capacity3.[]和iterator四、reserve和resize五、尾插尾删六、其他构造1.迭代器区间构造2.拷贝构造七、memcpy问题八、完整代码一、前言 在模拟实现容器时候࿰…...
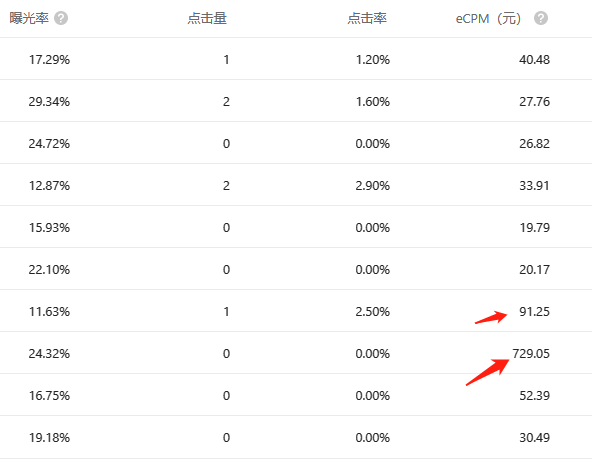
微信小程序、小游戏的流量主一般可以赚多少钱?
本篇文章主要科普小程序、小游戏流量主一般赚钱的实际情况,通过在下长期运营的经验汇总而成。 日期:2023年2月26日 作者:任聪聪 小程序、小程序满1000用户后即可开通流量主,但实际上很多人并没有传说中的那种日赚几千的流量收入的…...
jni-Demo-基于linux(c++ java)
跑一个jni 的最简单的Demo需要提前准备 VsCode 编译器、win10下,vscode中集成linux操作系统、c编译器(gcc、g),java编译器(jdk1.8)参考:https://mangocool.com/1653030123842.htmlJniDemo类&…...
指针的进阶——(1)
本次讲解重点: 1、字符指针 2、数组指针 3、指针数组 4、数组传参和指针传参 5、函数指针 关于指针这个知识点的主题,我们在前面已经初级阶段已经对指针有了大致的理解和应用了。我们知道了指针的概念: 1、指针就是地址,但口…...

电商平台的促销活动如何抵御大流量的ddos攻击
每一次活动大促带来的迅猛流量,对技术人而言都是一次严峻考验。如果在活动期间遭受黑产恶意 DDoS 攻击,无疑是雪上加霜。电商的特性是业务常态下通常不会遭受大流量 DDoS 攻击,且对延迟敏感,因此只需要在活动期间按需使用 DDoS 防…...

代码随想录-48-104. 二叉树的最大深度
目录前言题目1.层序迭代思路2. 本题思路分析:3. 算法实现4. pop函数的算法复杂度5. 算法坑点前言 在本科毕设结束后,我开始刷卡哥的“代码随想录”,每天一节。自己的总结笔记均会放在“算法刷题-代码随想录”该专栏下。 代码随想录此题链接 …...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
