Unit2_1:动态规划DP
文章目录
- 一、介绍
- 二、0-1背包问题
- 问题描述
- 分析
- 伪代码
- 时间复杂度
- 三、钢条切割问题
- 问题描述
- 分析
- 伪代码
- 过程
- 四、矩阵链乘法
- 背景
- 性质
- 分析
- 案例
- 伪代码
一、介绍
动态规划类似于分治法,它们都将一个问题划分为更小的子问题
最优子结构:问题的最优解包含子问题的最优解。DP适用的原因就在这
当子问题重叠时,即它们共享公共子问题时,可减小时间复杂度
DP通常用于优化问题,有许多解决方案的问题,我们想找到最好的一个
DP问题的求解思路一般就是
先描述最优解的结构
递归地定义最优解的值
计算最优解的值(通常是自下而上)
根据计算出的信息构造最优解(如果需要)
二、0-1背包问题
问题描述
n 个商品 , v i 表示第 i 个物品的价值 , w i 表示第 i 个物品的重量 一个能装入 W 重的背包 , 使用背包装下价值最多的物品 限制条件 : 我们不能取物品的一部分,我们取整个物品,或者什么都不取。 ( 这就是为什么它被称为 0 − 1 背包。 ) n个商品,v_i表示第i个物品的价值,w_i表示第i个物品的重量\\ 一个能装入W重的背包,使用背包装下价值最多的物品\\ 限制条件:我们不能取物品的一部分,我们取整个物品,或者什么都不取。\\(这就是为什么它被称为0-1背包。) n个商品,vi表示第i个物品的价值,wi表示第i个物品的重量一个能装入W重的背包,使用背包装下价值最多的物品限制条件:我们不能取物品的一部分,我们取整个物品,或者什么都不取。(这就是为什么它被称为0−1背包。)
分析
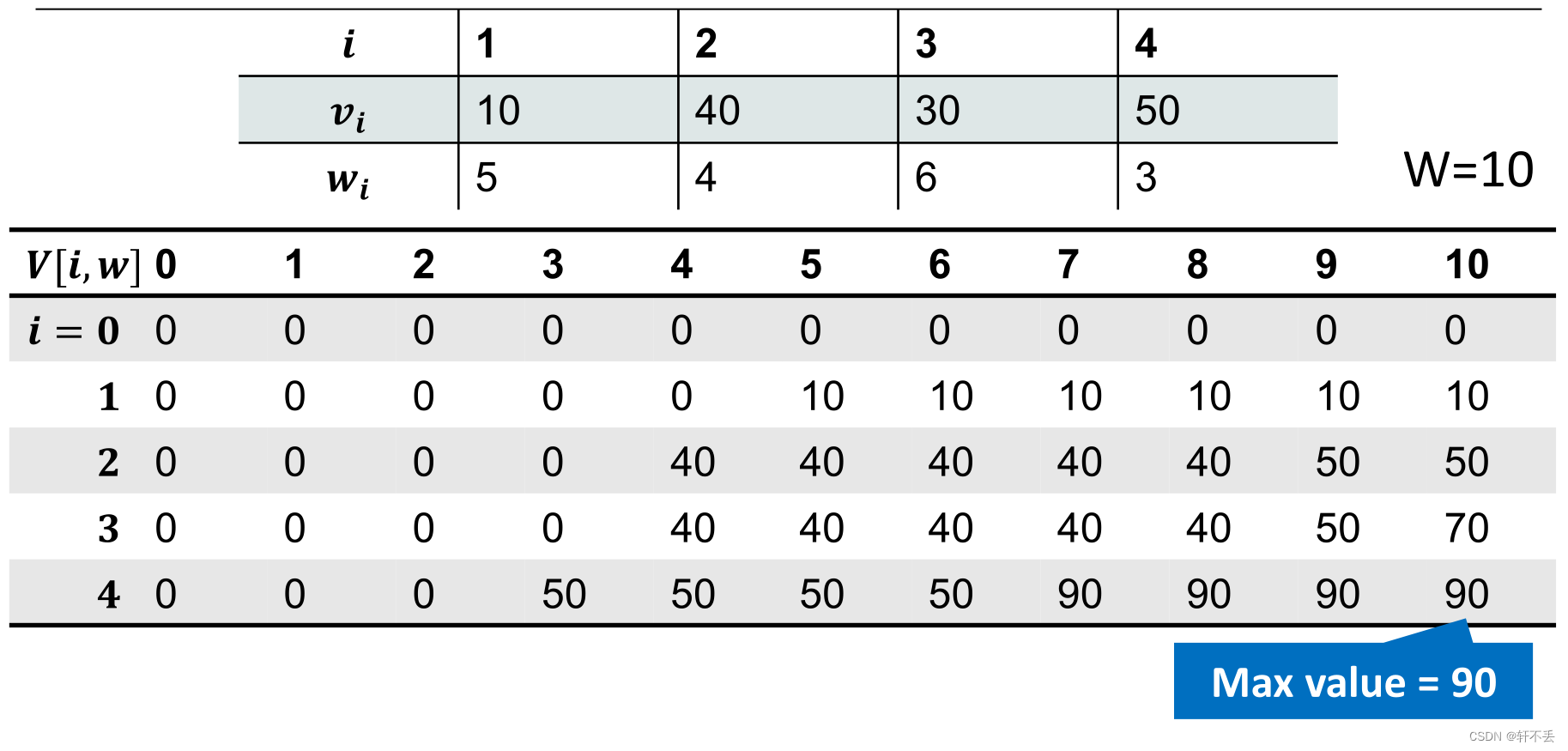
设 V [ i , w ] 表示重量为 w 背包 , 在前 i 种商品选择的最大价值 V[i,w]表示重量为w背包,在前i种商品选择的最大价值 V[i,w]表示重量为w背包,在前i种商品选择的最大价值
对于第i个物品,我们要么选取它,要么不选择,因此最大价值转移方程为
V [ i , w ] = m a x ( V [ i − 1 , w ] , v i + V [ i − 1 , w − w i ] ) V[i,w]=max(V[i-1,w],v_i+V[i-1,w-w_i]) V[i,w]=max(V[i−1,w],vi+V[i−1,w−wi])
若使用递归重复计算很多值,时间复杂度为 T ( n ) = O ( 2 W ) T(n)=O(2^W) T(n)=O(2W),因此要重复利用最优子结构的性质.
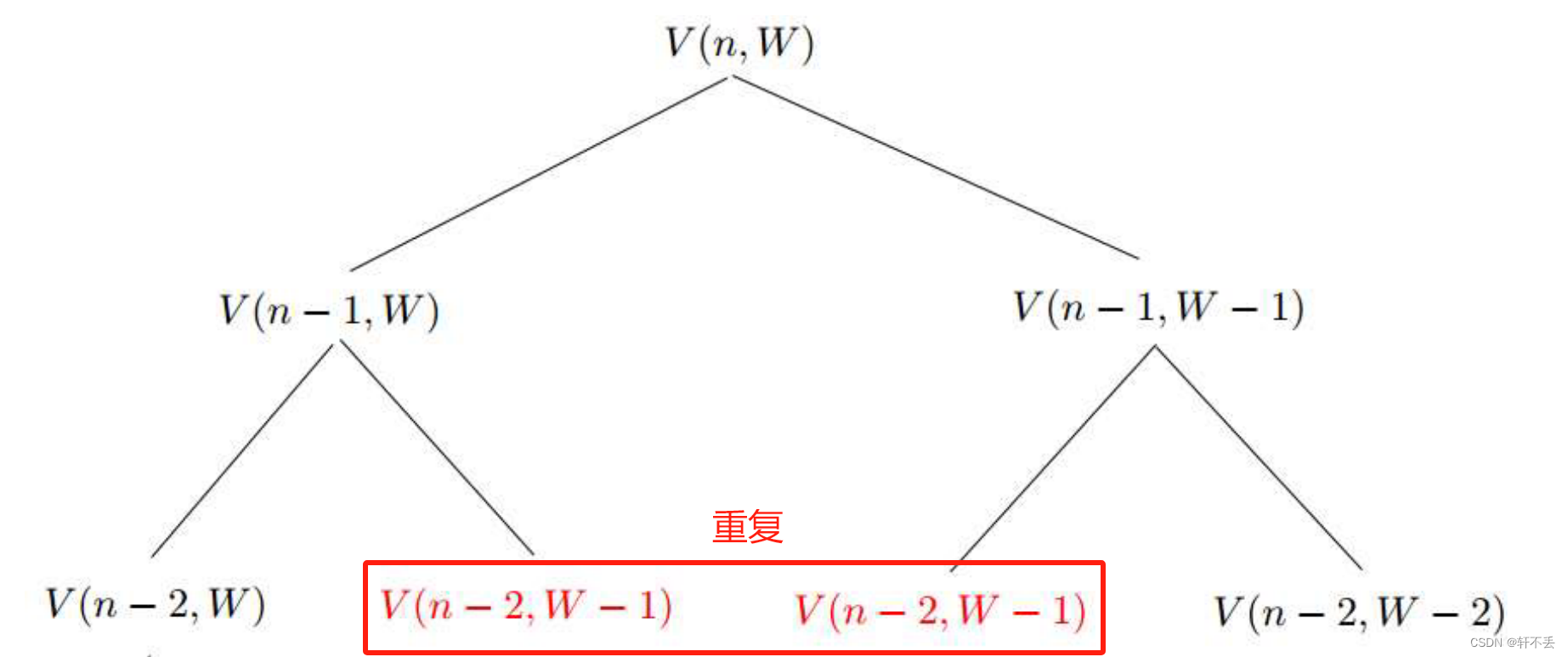
初始化: V [ 0 , w ] = 0 V[0,w]=0 V[0,w]=0 f o r for for 0 ≤ w ≤ W 0 \leq w \leq W 0≤w≤W 此时没有商品,自然没有价值
接下来按顺序填表:

伪代码
Knapsack(v,w,n,W)
for w=0 to W doV[0,w]=0;
end
for i=1 to n dofor w=0 to Wif w[i]<W thenV[i,w] = max{V[i-1,w],v[i]+V[i-1,w-w[i]]}elseV[i,w] = V[i-1,w]endend
end
return V[n,W]
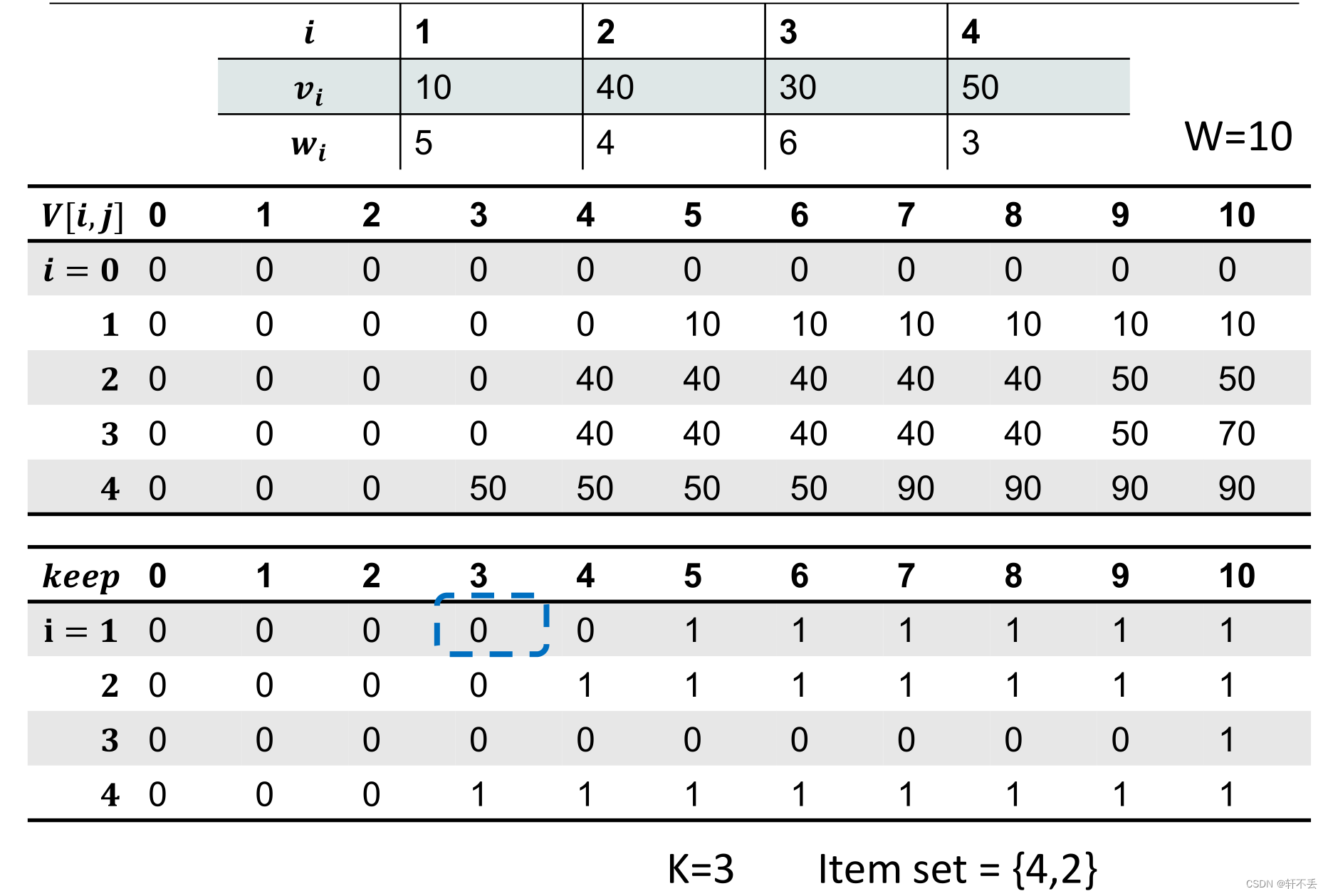
若是想要记录最优解的路径,需要维护一个 k e e p [ i ] [ w ] keep[i][w] keep[i][w],如果选择i作为 V [ i , w ] V[i,w] V[i,w],则 k e e p [ i ] [ w ] = 1 keep[i][w]=1 keep[i][w]=1
路径只需要
i f k e e p [ n , w ] = 1. 则选择 n 且继续从 k e p p [ n − 1 ] [ w − w n ] 开始 if keep[n,w]=1.则选择n且继续从kepp[n-1][w-w_n]开始 ifkeep[n,w]=1.则选择n且继续从kepp[n−1][w−wn]开始
i f k e e p [ n , w ] = 0. 则不选择 n 且继续从 k e p p [ n − 1 ] [ w ] 开始 if keep[n,w]=0.则不选择n且继续从kepp[n-1][w]开始 ifkeep[n,w]=0.则不选择n且继续从kepp[n−1][w]开始
因此路径输出代码:
K ← W
for i ← n to 1 doif keep[i][K] is equal to 1 thenOutput iK ← K-w[i]end
end
时间复杂度
两层循环,时间复杂度 T ( n ) = O ( n W ) T(n)=O(nW) T(n)=O(nW)
本质上,DP问题是用空间换时间,将结果放在空间中而不用下次花费时间再去计算
三、钢条切割问题
问题描述
给定一个长度为 n 的棒材和一个价格表,其中 p i 为长度为 i 的棒材的价格 确定最大的收入 r n , 以及切割钢条的方案 给定一个长度为n的棒材和一个价格表,其中pi为长度为i的棒材的价格\\ 确定最大的收入r_n,以及切割钢条的方案 给定一个长度为n的棒材和一个价格表,其中pi为长度为i的棒材的价格确定最大的收入rn,以及切割钢条的方案
分析
此题暴力解法,即遍历长度.每个点有两种选择,切 o r or or不切,判断哪种选择最合适即可,时间复杂度 T ( n ) = O ( 2 n ) T(n)=O(2^n) T(n)=O(2n).
考虑到最优子结构,可利用较短的杆最优收益来确定较长的,此题的状态转移如下:
r n = m a x ( p n , r 1 + r n − 1 , r 2 + r n − 2 , . . . . . , r n − 1 + r 1 ) r_n=max(p_n,r_1+r_{n-1},r_2+r_{n-2},.....,r_{n-1}+r_1) rn=max(pn,r1+rn−1,r2+rn−2,.....,rn−1+r1)
简化定义:
r n = m a x ( p i + r n − i ) r_n=max(p_i+r_{n-i}) rn=max(pi+rn−i) 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n
伪代码
r[0] ← 0
for j ← 0 to n doq ← -∞for i ← 1 to j doq ← max(q,p[i]+r[j-i])endr[j] ← q if j != 0
end
return r[n]
这种做法时间复杂度 T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
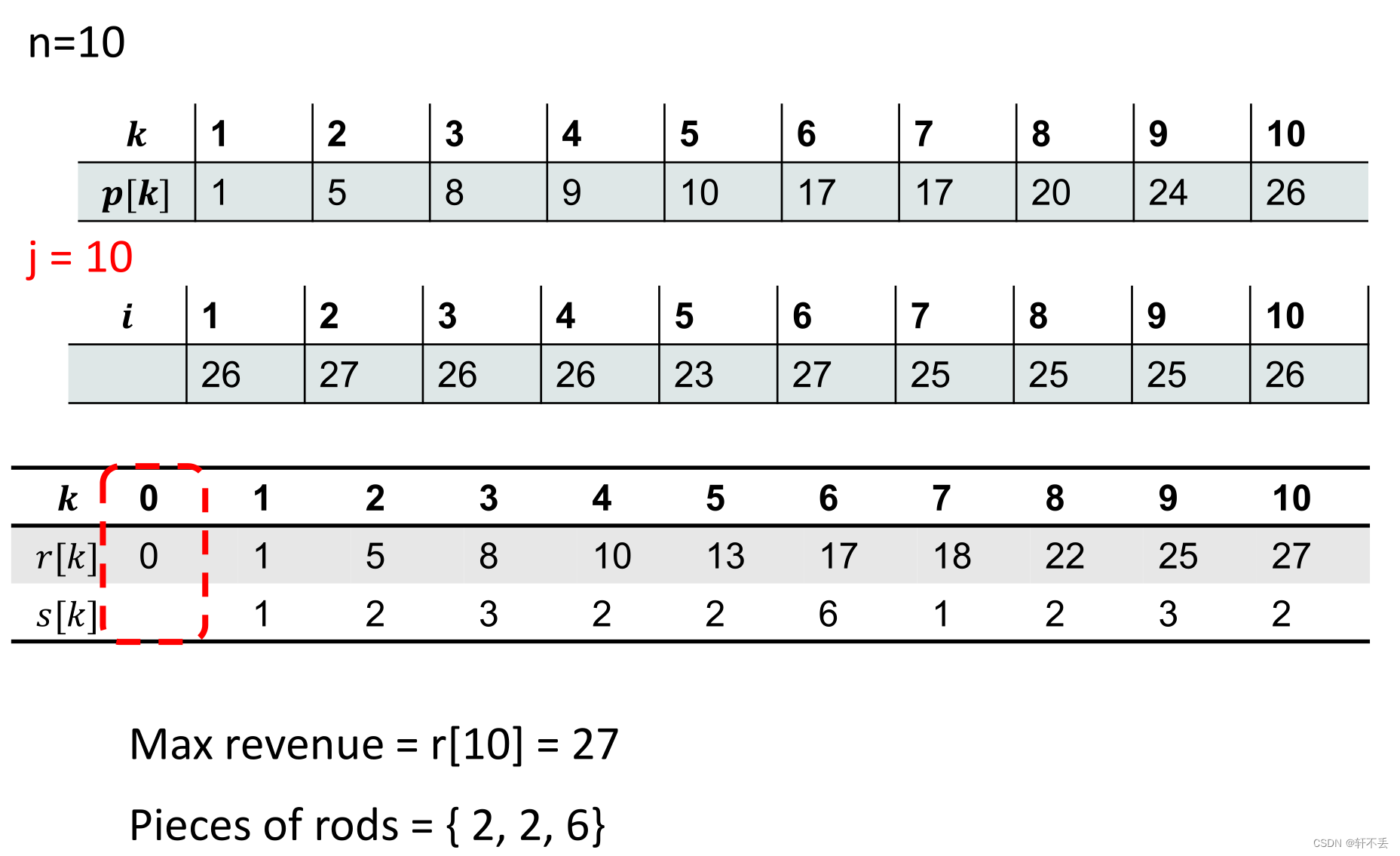
若是需要保存切割的方案,则需要维护一个 s [ n ] s[n] s[n]数组. s [ n ] 保存前一次切割的长度 s[n]保存前一次切割的长度 s[n]保存前一次切割的长度:
r[0] ← 0
for j ← 0 to n doq ← -∞for i ← 1 to j doif q < p[i]+r[j-i] thenq ← p[i]+r[j-i]s[j] ← iendendr[j] ← q if j != 0
end
while n>0 doOutput s[n]n ← n-s[n]
end
过程
四、矩阵链乘法
背景
p × q 矩阵 a 和 q × r 矩阵 B 的乘积 C = A B 是 p × r 矩阵 p × q矩阵a和q × r矩阵B的乘积C = AB是p × r矩阵 p×q矩阵a和q×r矩阵B的乘积C=AB是p×r矩阵
c [ i ] [ j ] = ∑ k = 1 q a [ i ] [ k ] b [ k ] [ j ] c[i][j]=\sum_{k=1}^{q}a[i][k]b[k][j] c[i][j]=∑k=1qa[i][k]b[k][j] f o r for for 1 ≤ i ≤ p 1 \leq i \leq p 1≤i≤p a n d and and 1 ≤ j ≤ r 1 \leq j \leq r 1≤j≤r
时间复杂度:注意 C C C有 p r pr pr个条目,每个条目需要 O ( q ) O(q) O(q)时间来计算,所以整个过程需要 O ( p q r ) O(pqr) O(pqr)时间
性质
矩阵乘法有结合律, A 1 A 2 A 3 = ( A 1 A 2 ) A 3 = A 1 ( A 2 A 3 ) A_1A_2A_3=(A_1A_2)A_3=A_1(A_2A_3) A1A2A3=(A1A2)A3=A1(A2A3)
因此当计算 A B C ABC ABC时,有两种选择, ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
m u l t [ ( A B ) C ] = p q r + p r s mult[(AB)C]=pqr+prs mult[(AB)C]=pqr+prs
m u l t [ A ( B C ) ] = q r s + p q s mult[A(BC)]=qrs+pqs mult[A(BC)]=qrs+pqs
每种选择的时间复杂度不一样
因此矩阵链乘法需要解决的就是怎么样结合能使得计算的量最小
分析
令 A i . . j = A i A i + 1 . . . A j 令A_{i..j}=A_iA_{i+1}...A{j} 令Ai..j=AiAi+1...Aj,显然, A i . . j A_{i..j} Ai..j是 P i − 1 × P j P_{i-1}×P_j Pi−1×Pj的矩阵
A i . . j A_{i..j} Ai..j可以表示为 A i . . j = ( A i . . . A k ) ( A k + 1 . . . A j ) = A i . . k A k + 1.. j A_{i..j}=(A_i...A_k)(A_{k+1}...A{j})=A_{i..k}A_{k+1..j} Ai..j=(Ai...Ak)(Ak+1...Aj)=Ai..kAk+1..j
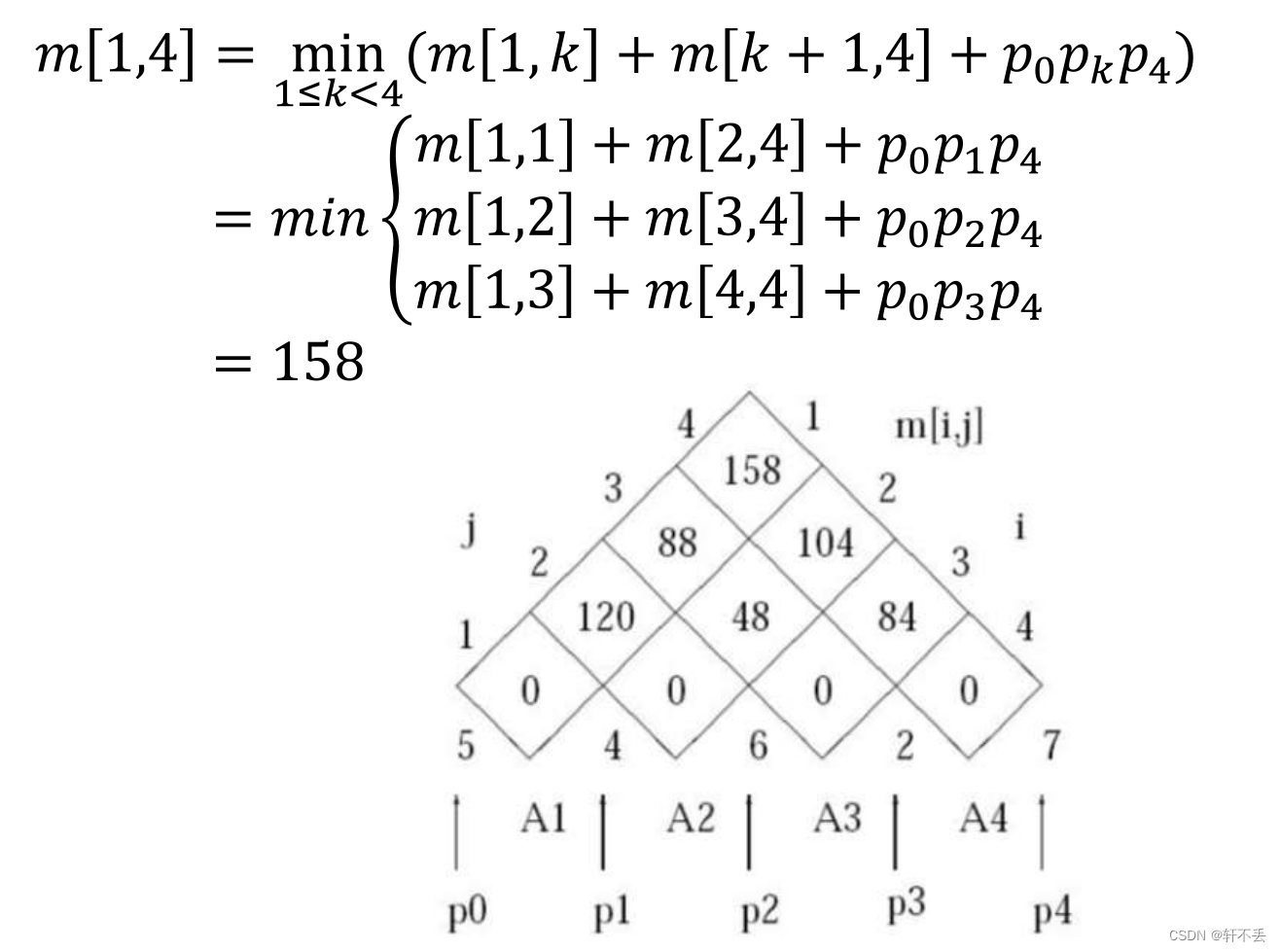
当 1 ≤ i ≤ j ≤ n 1 \leq i \leq j \leq n 1≤i≤j≤n时,令 m [ i , j ] m[i,j] m[i,j]表示计算 A i . . j A_{i..j} Ai..j所需的最小乘法次数。最优成本可以用下面的递归定义来描述
m ( i , j ) = { 0 i f i = j m i n i ≤ k ≤ j ( m ( i , k ) + m ( k + 1 , j ) + p i − 1 p k p j ) i f n = 1 m(i,j)=\left\{ \begin{array}{ll} 0 & if \space i=j \\ min_{i \leq k \leq j} (m(i,k)+m(k+1,j)+p_{i-1}p_kp_j)& if \space n=1 \nonumber \end{array} \right. m(i,j)={0mini≤k≤j(m(i,k)+m(k+1,j)+pi−1pkpj)if i=jif n=1
注意计算并保存 m [ i , j ] m[i, j] m[i,j]的顺序是,当计算 m [ i , j ] m[i, j] m[i,j]时, m [ i , k ] m[i, k] m[i,k]和 m [ k + 1 , j ] m[k + 1, j] m[k+1,j]的值已经可用,因此按矩阵链长度的递增顺序计算它们:
m [ 1 , 2 ] , m [ 2 , 3 ] , m [ 3 , 4 ] , … , m [ n − 3 , n − 2 ] , m [ n − 2 , n − 1 ] , m [ n − 1 , n ] m[1,2], m[2,3], m[3,4],…, m[n-3,n-2], m[n-2,n-1], m[n-1,n] m[1,2],m[2,3],m[3,4],…,m[n−3,n−2],m[n−2,n−1],m[n−1,n]
m [ 1 , 3 ] , m [ 2 , 4 ] , m [ 3 , 5 ] , … , m [ n − 3 , n − 1 ] , m [ n − 2 , n ] m[1,3], m[2,4], m[3,5],…, m[n-3,n-1], m[n-2,n] m[1,3],m[2,4],m[3,5],…,m[n−3,n−1],m[n−2,n]
m [ 1 , 4 ] , m [ 2 , 5 ] , m [ 3 , 6 ] , … , m [ n − 3 , n ] m[1,4], m[2,5], m[3,6],…, m[n-3,n] m[1,4],m[2,5],m[3,6],…,m[n−3,n]
… … …
m [ 1 , n − 1 ] , m [ 2 , n ] m[1,n-1], m[2,n] m[1,n−1],m[2,n]
m [ 1 , n ] m[1,n] m[1,n]
若需要记录分隔括号路径,需要维护一个二维数组 s [ 1.. n , 1.. n ] s[1..n, 1..n] s[1..n,1..n],里面存储 A i . . j A_{i..j} Ai..j的最优分隔k
s [ 1 , n ] s[1,n] s[1,n] ( A 1 . . A s [ 1 , n ] ) ( A s [ 1 , n ] + 1 . . . A n ) (A_1..A_{s[1,n]})(A_{s[1,n]+1}...A{n}) (A1..As[1,n])(As[1,n]+1...An)
s [ 1 , s [ 1. n ] ] s[1,s[1.n]] s[1,s[1.n]] ( A 1 . . A s [ 1 , s [ 1. n ] ] ) ( A s [ 1 , s [ 1. n ] ] + 1 . . . A n ) (A_1..A_{s[1,s[1.n]]})(A_{s[1,s[1.n]]+1}...A{n}) (A1..As[1,s[1.n]])(As[1,s[1.n]]+1...An)
案例
伪代码
MatrixChain(p,n)
for i ← 1 to n dom[i,i] ← 0;
end
for l ← 2 to n dofor i ← 1 to n-l+1 doj ← i+l-1;m[i,j] ← ∞for k ← i to j-1 doq ← m[i,k]+m[k+1,j]+p[i-1]*p[k]*p[j]if q<m[i,j] thenm[i,j] ← qs[i,j] ← kendendend
end
return m[1,n] and s
三层循环,时间复杂度 T ( n ) = O ( n 3 ) T(n)=O(n^3) T(n)=O(n3)
相关文章:

Unit2_1:动态规划DP
文章目录 一、介绍二、0-1背包问题问题描述分析伪代码时间复杂度 三、钢条切割问题问题描述分析伪代码过程 四、矩阵链乘法背景性质分析案例伪代码 一、介绍 动态规划类似于分治法,它们都将一个问题划分为更小的子问题 最优子结构:问题的最优解包含子问题的最优解。DP适用的原…...
k8s提交spark应用消费kafka数据写入elasticsearch7
一、k8s集群环境 k8s 1.23版本,三个节点,容器运行时使用docker。 spark版本时3.3.3 k8s部署单节点的zookeeper、kafka、elasticsearch7 二、spark源码 https://download.csdn.net/download/TT1024167802/88509398 命令行提交方式 /opt/module/spark…...
linux傻瓜式安装Java环境及中间件
linux配置Java环境及中间件 1.傻瓜式安装Java1.下载2.追加3.刷新测试 2.傻瓜式安装docker1.docker卸载2.docker安装 3.Docker傻瓜式安装Redis1.傻瓜式安装安装并配置 4.Docker傻瓜式安装RabbitMQ5.Docker傻瓜式安装MySql1.拉取2.配置 6.傻瓜式安装Nacos1.官网下载nacos2.SQL文件…...

javascript中的new原理及实现
在js中,我们通过new运算符来创建一个对象,它是一个高频的操作。我们一般只是去用它,而很少关注它是如何实现的,它的工作机制是什么。 1 简介 本文介绍new的功能,用法,补充介绍了不加new也同样创建对象的方…...

R语言 PPT 预习+复习
什么狗吧发明的结业考,站出来和我对线 第一章 绪论 吊码没有,就算考R语言特点我也不背,问就是叫么这没用。 第二章 R语言入门 x<-1:20 赋值语句 x 1到20在x上添加均值为0、标准差为2的正态分布噪声 y <- x rnorm (20, 0, 2) 这…...

轻松实现固定资产智能管理的工具来了
易点易动资产管理系统是一款旨在轻松实现智能资产管理的工具。固定资产管理对于企业的日常经营和可持续发展至关重要。然而,固定资产具有设备价值高、使用周期长、使用地点分散、使用环境恶劣、流动性强、安全管理难度大等特点,传统的管理方式往往无法高…...

软考高级系统架构设计师系列之:微服务
软考高级系统架构设计师系列之:微服务 一、微服务二、微服务的优势三、微服务挑战四、微服务与SOA的对比一、微服务 微服务架构建议将大型复杂的单体架构应用划分为一组微小的服务,每个微服务根据其负责的具体业务职责提炼为单一的业务能力。每个服务可以很容易地部署并发布…...
vue + axios + mock
参考来源:Vue mock.js模拟数据实现首页导航与左侧菜单功能_vue.js_AB教程网 记录步骤:在参考资料来源添加axios步骤 1、安装mock依赖 npm install mock -D //只在开发环境使用 下载完成后,项目文件package.json中的devDependencies就会加…...

Mongoose 开源库--json 使用笔记
一、 json相关API mongoose 开源库可以使用json进行数据处理。 ①创建json字符串 // A helper macro for printing JSON: mg_snprintf(buf, len, "%m", MG_ESC("hi")) #define MG_ESC(str) mg_print_esc, 0, (str) char *mg_mprintf(const char *fmt, ...)…...

linux中复制文件如何排除一个目录
误区: 首先使用cp命令的 --exclude参数实不可取的,会造成以下的报错,因为cp命令中压根就没有--exclude这个参数的配置 cp: unrecognized option --exclude‘****’ 问题解决: 我们可以使用rsync工具来完成目录排除的功能&#x…...
时空智友企业信息管理系统任意文件读取漏洞复现
简介 时空智友企业信息管理系统是一个用于企业流程管理和控制的软件系统。它旨在帮助企业实现流程的规范化、自动化和优化,从而提高工作效率、降低成本并提升管理水平。 时空智友企业信息管理系统存在任意文件读取漏洞,攻击者可以在未授权的情况下读取…...

YOLOv8优化:block系列篇 | Neck系列篇 |可重参化EfficientRepBiPAN优化Neck
🚀🚀🚀本文改进: 可重参化EfficientRepBiPAN优化Neck 如何在YOLOv8下使用:1)结合neck; 🚀🚀🚀EfficientRepBiPAN在各个领域都有ying 🚀🚀🚀YOLOv8改进专栏:http://t.csdnimg.cn/hGhVK 学姐带你学习YOLOv8,从入门到创新,轻轻松松搞定科研; 1.原理…...
零代码编程:用ChatGPT批量提取flash动画swf文件中的mp3
文件夹:C:\迅雷下载\有声绘本_flash[淘宝-珍奥下载]\有声绘本 flash,里面有多个flash文件,怎么转换成mp3文件呢? 可以使用swfextract工具从Flash动画中提取音频,下载地址是http://www.swftools.org/download.html,也…...
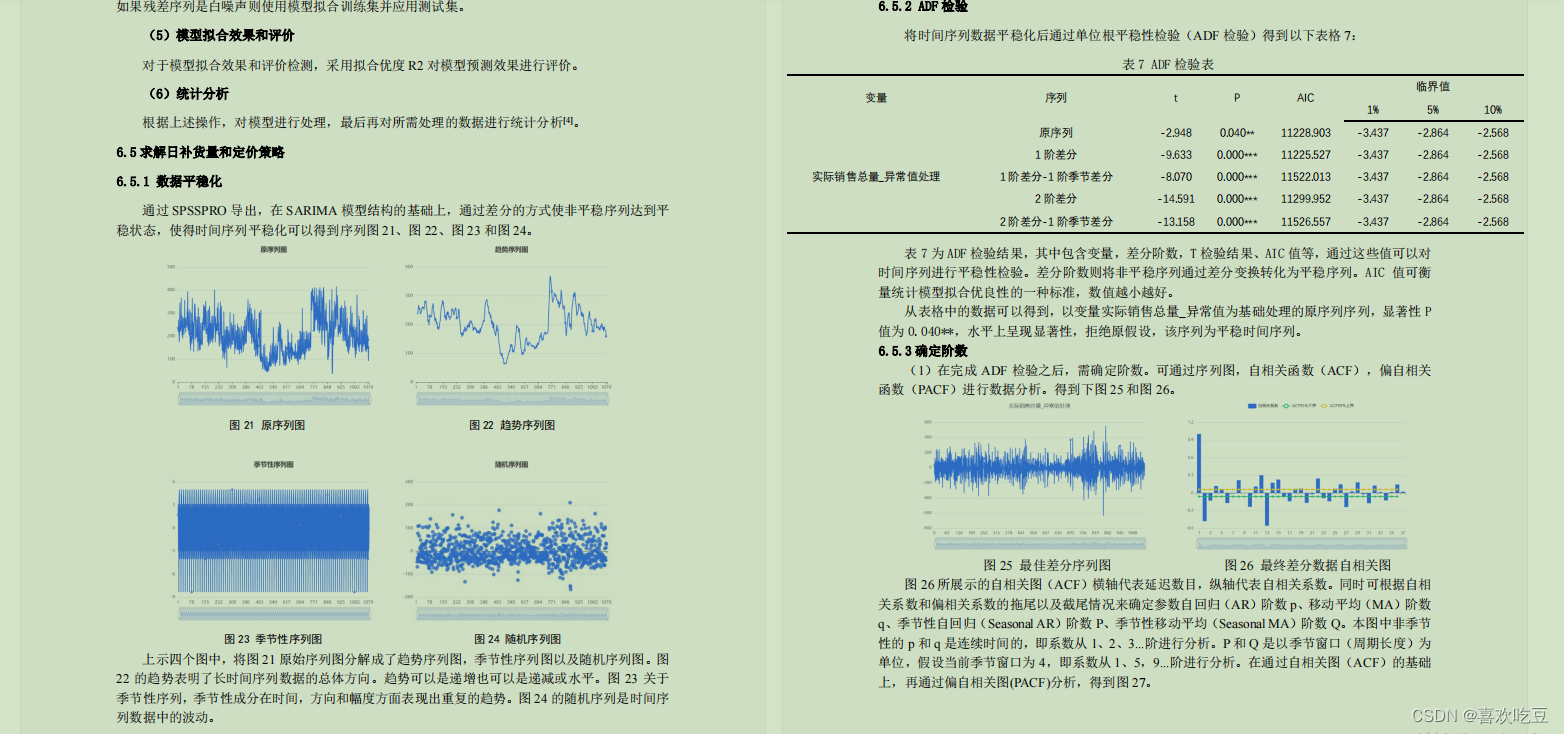
2023数学建模国赛C题赛后总结
今天国赛的成绩终于出来了,盼星星盼月亮的。之前面试的时候已经把我给推到国奖评委那里去了,可是好可惜,最终以很微小的劣势错失国二。只拿到了广西区的省一。我心里还是很遗憾的,我真的为此准备了很久,虽然当中也有着…...
)
hiveSQL语法及练习题整理(mysql)
目录 hiveSQL练习题整理: 第一题 第二题 第三题 第四题 第五题 第六题 第七题 第八题 第九题 第十题 第十一题 第十二题 hivesql常用函数: hiveSQL常用操作语句(mysql) hiveSQL练习题整理: 第一题 我…...
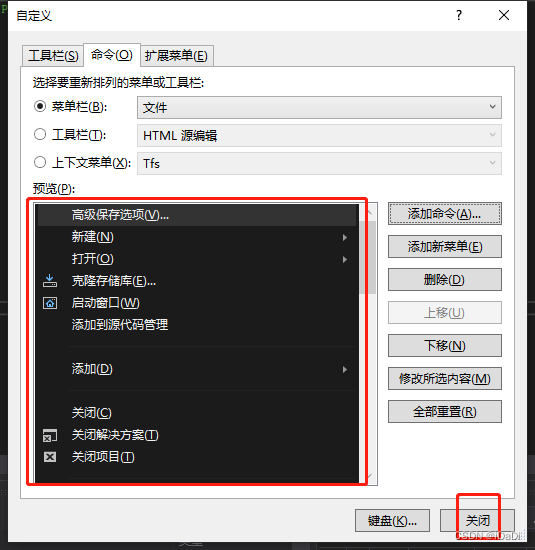
【UE4】UE编辑器乱码问题
环境:UE4.27、vs2019 如何解决 问题原因,UE的编码默认是UTF-8,VS的默认编码是GBK 通过"高级保存选项" 直接修改VS的 .h头文件 的 编码 为 UTF-8 步骤1. 步骤2. 修改编码后,从新编译,然后就可以解决编辑器…...
2 创建svelte项目(应用程序)
官网方式搭建: npm create sveltelatest my-app cd my-app npm install npm run dev 官网中介绍: 如果您使用的是 VS Code,安装 Svelte for VS Code 就可以了,以便语法高亮显示。 然后,一旦您的项目设置好了&#…...
手机怎么打包?三个方法随心选!
有的时候,电脑不在身边,只有随身携带的手机,这个时候又急需把文件打包发送给同事或者同学,如何利用手机操作呢?下面介绍了具体的操作步骤。 一、通过手机文件管理自带压缩功能打包 1、如果是iOS系统,就在手…...
SecureFX如何用Public key 連接sftp
點擊connection 右鍵點開站點的properties 點選SSH2--Authentication---Pulickey 先選擇Putty Key Generator save出來的public key(.pub)文件(Putty Key Generator 保存時可能沒加.pub後綴保存,可自行對public key加上後綴.pub) 同時注意要…...

BUUCTF 隐藏的钥匙 1
BUUCTF:https://buuoj.cn/challenges 题目描述: 路飞一行人千辛万苦来到了伟大航道的终点,找到了传说中的One piece,但是需要钥匙才能打开One Piece大门,钥匙就隐藏在下面的图片中,聪明的你能帮路飞拿到钥匙ÿ…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
