第七章 图【数据结构与算法】【精致版】
第七章 图【数据结构与算法】【精致版】
- 前言
- 版权
- 第七章 图
- 7.1 应用实例
- 7.2图的基本概念
- 7.3图的存储结构
- 7.3.1邻接矩阵
- **1-邻接矩阵.c**
- **2-邻接矩阵plus.c**
- 7.3.2 邻接表
- **3-邻接表.c**
- **4-邻接表plus.c**
- 7.3.3 十字链表
- 7.3.4多重链表
- 7.4图的遍历
- 7.4.1深度优先搜索遍历
- **5-DFSAdjMatrix.c**
- **6-DFSAdjList.c**
- 7.4.2广度优先搜索遍历
- **7-BFSAdjMatrix.c**
- **8-BFSAdjList.c**
- 7.5图的应用
- 7.5.1最小生成树
- **9-Prim.c**
- 7.5.2 拓扑排序
- **10-拓扑排序.c**
- 7.5.3关键路径
- 7.5.4最短路径
- **11-单源最短路径.c**
- **12-多源最短路径.c**
- 6实例分析与实现
- 7算法总结 贪心算法
- 习题7
- 3完成题 1 2 4 6
- 4.算法设计题
- (11)已知有向图以邻接表作为存储结构,编写算法判断该图中是否存在顶点V~i~到顶点V~j~,的简单路径,并输出该路径上的顶点。
- 最后
前言
2023-11-6 17:07:13
以下内容源自《【数据结构与算法】【精致版】》
仅供学习交流使用
版权
禁止其他平台发布时删除以下此话
本文首次发布于CSDN平台
作者是CSDN@日星月云
博客主页是https://jsss-1.blog.csdn.net
禁止其他平台发布时删除以上此话
第七章 图
7.1 应用实例
城市交通问题
7.2图的基本概念
图的定义:图是由顶点集V和弧集R构成的数据结构,Graph=(V,R)
其中:
V={v|v∈ DataObject}
R={VR}
VR={<v,w>|P(v,w)且(v,w∈V)}
<v,w>表示从顶点v到顶点w的一条弧,称为“弧尾”,w为“弧头”
谓词P(v,w)定义了弧<u,w>的意义或信息,表示从到w的一条单向通道。
苦<v,w>∈VR,必有<w,v>∈VR,则以(v,w)代替这两个有序对,称v和w之间存在一条边。
有向图:由顶点集和弧集构成的图称为“有向图”。
无向图:由顶点集和边集构成的图称为“无向图"。
有向网或无向网:有向图或无向图中的弧或边带权后的图分别称为“有向网"或“无向网”
子图:设图G=(V|{VR})和图G’=(V’|{VR’}),且V’⊆V,VR’⊆VR,则称G’为G的子图。
完全图:图中有n个顶点、n(n-1)/2条边的无向图称为“完全图”。
有向完全图;图中有n个顶点、n(n-1)条弧的有向图称为“有向完全图”
稀疏图:假设图中有n个顶点e条边(或弧),若边(或弧)的个数e<nlogn,则称为“稀疏图”, 否则称为“稠密图”
邻接点:若无向图中顶点v和w之间存在一条边(n,w),则称顶点v和w互为邻接点,称边 (r,w)依附于顶点n和w或边(v,w)与顶点v和w相关联。
顶点的度;在无向图中与顶点v关联的边的数目定义为v的度,记为TD(v)。
握手定理:可以看出,在无向图中,其总度数等于总边数的两倍。
对于有向图,若顶点v和w之间存在一条弧<u,w>,则称顶点v邻接到顶点w,顶点v邻接自 顶点v,称弧<v,w>与顶点u和w相关联。
以v为尾的弧的数目定义为v的出度,记为OD(v)。
以为头的弧的数目定义为v的入度,记为ID(v)。
顶点的度(TD)=出度(OD)+入度(ID)。
可以看出,在有向图中,其总人度、总出度和总强数相等
路径:设用G=(V|{VR}中的{u=vi,0,vi,1,…,vi,m=w}顶点序列中,有(vi,j-1,vi,j)∈VR(1<=j<=m),则称从顶点u到顶点w之间存在一条路径。路径上边的数目称为“路径长度”,有向图的路径也是有向的。
简单路径:顶点不重复的欧种称为“简单路径“
回路:首尾顶点相同的路径称为“回路“
简单回路:除了首尾顶点,中间任何一个顶点不重复的问路称为“简单回路”
连通图:在无向图中,若顶点Vi到Vj有路径存在,则称Vi和Vj是连通的。若无向图中任意两个顶点之间都有路径相通,即是连通的,则称此图为连通图,否则,称其为非连通图
无向图中各个极大连通子图称为该图的“连通分量”
强连通图:在有向图中,若任意两个顶点之间都存在一条有向路径,则称此有向图为“强连通图”;否则,称其为“非强连通图”。
有向图中各个极大强连通子图称为该图的强连通分量
生成树:包含连通图中全部项点的极小连通子图称为该图的“生成树”,即假设一个连通图有n个顶点和e条边,其中n个顶点和n-1条边构成一个极小连通子图,该极小连通子图为此连通图的生成树。对非连通图,由各个连通分量的生成树构成的集合称为该非连通图的“生成森林”
7.3图的存储结构
7.3.1邻接矩阵
图的邻接矩阵是表示顶点之间的相邻关系的矩阵,是顺序存储结构。
设图G是一个具有n个顶点的图,它的顶点集合V={v0,v1,v2,…,vn-1}则顶点之间的关系可用如下形式的矩阵A来描述,即矩阵A中每个元素A[i][j]满足
{ 1 若<v~i~,v~j~>或(v~i~,v~j~)∈VR
A[i][j] = {{ 0 反之对于带权图(网),邻接矩阵A中每个元素A[i][j]满足
{ weight 若<v~i~,v~j~>或(v~i~,v~j~)∈VR
A[i][j] = {{ ∞ 反之邻接矩阵的数据类型描述为:
#include<stdio.h>
#include<stdlib.h>
#define MAXVEX 20 //最大顶点个数
#define INFINITY 32768 //表示极大值
typedef int Vextype;
typedef struct{int arcs[MAXVEX][MAXVEX]; //边(或弧)信息Vextype vex[MAXVEX]; //顶点信息,顶点类型根据实际情况自行定义int vexnum; //顶点数目int arcnum; //边(或弧)数目
}AdjMatrix;//邻接矩阵
1-邻接矩阵.c
只针对无向网
//邻接矩阵的数据类型描述为:
#include<stdio.h>
#include<stdlib.h>
#define MAXVEX 20 //最大顶点个数
#define INFINITY 32768 //表示极大值
typedef int Vextype;
typedef struct{int arcs[MAXVEX][MAXVEX]; //边(或弧)信息Vextype vex[MAXVEX]; //顶点信息,顶点类型根据实际情况自行定义int vexnum; //顶点数目int arcnum; //边(或弧)数目
}AdjMatrix;//邻接矩阵
//【算法7.1】用邻接矩阵创建无向网
void Create(AdjMatrix *G){int i,j,k,weight,vex1,vex2;printf("请输入无向网中的顶点数和边数:\n"); scanf("%d,%d",&G->vexnum,&G->arcnum); for(i=1;i<=G->vexnum;i++){for(j=1;j<=G->vexnum;j++){G->arcs[i][j]=INFINITY;//如果不是网,则赋值0}} printf("请输入无向网中%d个顶点:\n",G->vexnum); for(i=1;i<=G->vexnum;i++){printf("No.%d个顶点:顶点V:",i); scanf("%d", &G->vex[i]);} printf("\n请输入无向网中%d条边:",G->arcnum); for(k=0;k<G->arcnum;k++){printf("\nNo.%d条边:\n",k+1); printf("顶点V:"); scanf("%d",&vex1);printf ("<--->顶点V:");scanf ("%d",&vex2);printf("权值:");scanf("%d", &weight);G->arcs[vex1][vex2] =weight;//如果不是网,则赋值1 G->arcs[vex2][vex1] =weight;//如果是有向网,删掉此句}}
void Printf(AdjMatrix* G){printf("共有%d个顶点",G->vexnum);printf("共有%d条边",G->arcnum);printf("\n");int i,j;printf("\\ ");for(i=1;i<=G->vexnum;i++){printf("%-5d ",G->vex[i]);}printf("\n");for(i=1;i<=G->vexnum;i++){printf("%-5d ",G->vex[i]);for(j=1;j<=G->vexnum;j++){ printf("%-5d ",G->arcs[i][j]);}printf("\n");}
}void main(){AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));Create(G);Printf(G);}
运行结果如下
2-邻接矩阵plus.c
适用于各种类型的图
//邻接矩阵的数据类型描述为:
#include<stdio.h>
#include<stdlib.h>#define MAXVEX 20 //最大顶点个数
#define INFINITY 32768 //表示极大值
typedef enum GraghType{UG=1,DG,UN,DN
}GT;
typedef int Vextype;
typedef struct{int arcs[MAXVEX][MAXVEX]; //边(或弧)信息Vextype vex[MAXVEX]; //顶点信息,顶点类型根据实际情况自行定义int vexnum; //顶点数目int arcnum; //边(或弧)数目GT t;
}AdjMatrix;//邻接矩阵
void type(GT t){switch(t){case UG:printf("无向图");break; case DG:printf("有向图");break; case UN:printf("无向网");break; case DN:printf("无向网");break; }}
//【算法7.1】用邻接矩阵创建无向网
void Create(AdjMatrix *G){GT t=G->t;int i,j,k,weight,vex1,vex2;printf("请输入"); type(t);printf("中的顶点数和边数:\n");scanf("%d,%d",&G->vexnum,&G->arcnum); for(i=1;i<=G->vexnum;i++){for(j=1;j<=G->vexnum;j++){G->arcs[i][j]=INFINITY;//如果不是网,则赋值0}} printf("请输入"); type(t); printf("中%d个顶点:\n",G->vexnum); for(i=1;i<=G->vexnum;i++){printf("No.%d个顶点:顶点V:",i); scanf("%d", &G->vex[i]);} printf("\n请输入"); type(t);printf("中%d条边:",G->arcnum); for(k=0;k<G->arcnum;k++){printf("\nNo.%d条边:\n",k+1); printf("顶点V:"); scanf("%d",&vex1);printf ("<--->顶点V:");scanf ("%d",&vex2);printf("权值:");scanf("%d", &weight);if(G->t==1||G->t==2){weight=1;}G->arcs[vex1][vex2] =weight;//如果不是网,则赋值1if(G->t==1||G->t==3){G->arcs[vex2][vex1] =weight;//如果是有向网,删掉此句} }}
void Printf(AdjMatrix* G){printf("图的类型:");type(G->t);printf("\n");printf("共有%d个顶点",G->vexnum);printf("共有%d条边",G->arcnum);printf("\n");int i,j;printf("\\ ");for(i=1;i<=G->vexnum;i++){printf("%-5d ",G->vex[i]);}printf("\n");for(i=1;i<=G->vexnum;i++){printf("%-5d ",G->vex[i]);for(j=1;j<=G->vexnum;j++){ printf("%-5d ",G->arcs[i][j]);}printf("\n");}
}void main(){printf("创建\n");AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("打印\n");Printf(G);} 运行结果如下
7.3.2 邻接表
邻接表由边表和顶点表组成。
边表就是对图中的每一个顶点建立一条单链表,表中存放与该顶点邻接的所有顶点,相当于邻接矩阵的所有非零元素。
顶点表用于存放图中每一个顶点的信息以及指向改顶点边表的头指针。
顶点结构
vexdata head
图的边结构
adjvex next
网的边结构
adjvex weight next
邻接矩阵的数据类型描述为:
#include<stdio.h>
#include<stdlib.h>
#define MAXVEX 20
typedef struct ArcNode{int adjvex;int weight;struct ArcNode *next;
}ArcNode;3-邻接表.c
只针对无向网
//邻接矩阵的数据类型描述为:
#include<stdio.h>
#include<stdlib.h>
#define MAXVEX 20
typedef struct ArcNode{int adjvex;int weight;struct ArcNode *next;
}ArcNode;typedef struct VertexNode{char vexdata; ArcNode *head;
}VertexNode;typedef struct {VertexNode vertex[MAXVEX];int vexnum;//顶点数 int arcnum;//弧数
}AdjList;//用邻接表创建无向网
void Create(AdjList *G){int i,j,k,weight,vex1,vex2;printf("请输入无向网中的顶点数和边数:\n"); scanf("%d,%d",&G->vexnum,&G->arcnum); printf("请输入无向网中%d个顶点:\n",G->vexnum); for(i=1;i<=G->vexnum;i++){ VertexNode v; printf("No.%d个顶点:顶点V:",i);char c=getchar();
// if(c=='\n'){
// c=getchar();
// }fflush(stdin); scanf("%c",&v.vexdata);
// v.vexdata=c;v.head=(ArcNode*)malloc(sizeof(ArcNode));G->vertex[i]=v;} printf("\n请输入无向网中%d条边:",G->arcnum); for(k=0;k<G->arcnum;k++){printf("\nNo.%d条边:\n",k+1); printf("顶点V:"); scanf("%d",&vex1);printf ("<--->顶点V:");scanf ("%d",&vex2);printf("权值:");scanf("%d", &weight);ArcNode *r1;r1=G->vertex[vex1].head;ArcNode *r2;r2=G->vertex[vex2].head;ArcNode *s1=(ArcNode*)malloc(sizeof(ArcNode));ArcNode *s2=(ArcNode*)malloc(sizeof(ArcNode));s1->adjvex=vex2;s1->weight=weight;//如果不是网,则赋值1 r1->next=s1;s2->adjvex=vex1;s2->weight=weight;//如果不是网,则赋值1r2->next=s2;r1=s1;r2=s2;r1->next=NULL;r2->next=NULL;}}
void Printf(AdjList* G){printf("共有%d个顶点",G->vexnum);printf("共有%d条边",G->arcnum);printf("\n");int i,j;for(i=1;i<=G->vexnum;i++){printf("%c(%d) ",G->vertex[i].vexdata,i);ArcNode* p=G->vertex[i].head->next;while(p!=NULL){printf("--%d--",p->weight);printf("%c(%d) ",G->vertex[p->adjvex].vexdata,p->adjvex);p=p->next; }printf("\n");}}void main(){AdjList* G=(AdjList*)malloc(sizeof(AdjList));Create(G);Printf(G);}
运行结果如下
4-邻接表plus.c
适用于各种类型的图
//邻接矩阵的数据类型描述为:
#include<stdio.h>
#include<stdlib.h>
#define MAXVEX 20
typedef enum GraghType{UG=1,DG,UN,DN
}GT;
typedef struct ArcNode{int adjvex;int weight;struct ArcNode *next;
}ArcNode;typedef struct VertexNode{char vexdata; ArcNode *head;
}VertexNode;typedef struct {VertexNode vertex[MAXVEX];int vexnum;//顶点数 int arcnum;//弧数 GT t;
}AdjList;
void type(GT t){switch(t){case UG:printf("无向图");break; case DG:printf("有向图");break; case UN:printf("无向网");break; case DN:printf("有向网");break; }}
//用邻接表创建无向网
void Create(AdjList *G){GT t=G->t;int i,j,k,weight,vex1,vex2;printf("请输入"); type(t);printf("中的顶点数和边数:\n"); scanf("%d,%d",&G->vexnum,&G->arcnum); printf("请输入"); type(t); printf("中%d个顶点:\n",G->vexnum); for(i=1;i<=G->vexnum;i++){ VertexNode v; printf("No.%d个顶点:顶点V:",i);
// char c=getchar();
// if(c=='\n'){
// c=getchar();
// }fflush(stdin); scanf("%c",&v.vexdata);
// v.vexdata=c;v.head=(ArcNode*)malloc(sizeof(ArcNode));v.head->next=NULL;G->vertex[i]=v;} printf("\n请输入"); type(t);printf("中%d条边:",G->arcnum); for(k=0;k<G->arcnum;k++){printf("\nNo.%d条边:\n",k+1); printf("顶点V:"); scanf("%d",&vex1);printf ("<--->顶点V:");scanf ("%d",&vex2);printf("权值:");scanf("%d", &weight);if(G->t==1||G->t==2){weight=1;//如果不是网,则赋值1 }ArcNode *r1= G->vertex[vex1].head;//尾结点 while(r1->next!=NULL){r1=r1->next;}ArcNode *s1=(ArcNode*)malloc(sizeof(ArcNode)); s1->adjvex=vex2;s1->weight=weight;s1->next=r1->next;r1->next=s1;// r1->next=NULL;if(G->t==1||G->t==3){ArcNode *r2= G->vertex[vex2].head;//尾结点 while(r2->next!=NULL){r2=r2->next;}ArcNode *s2=(ArcNode*)malloc(sizeof(ArcNode));s2->adjvex=vex1;s2->weight=weight; s2->next=r2->next;r2->next=s2; // r2->next=NULL; }}}
void Printf(AdjList* G){printf("图的类型:");type(G->t);printf("\n");printf("共有%d个顶点",G->vexnum);printf("共有%d条边",G->arcnum);printf("\n");int i,j;for(i=1;i<=G->vexnum;i++){ArcNode* p=G->vertex[i].head->next;while(p!=NULL){printf("%c(%d) ",G->vertex[i].vexdata,i);printf("--%d--",p->weight);printf("%c(%d) ",G->vertex[p->adjvex].vexdata,p->adjvex);p=p->next; }printf("\n");}}void main(){AdjList* G=(AdjList*)malloc(sizeof(AdjList));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);Printf(G);}
运行结果如下
7.3.3 十字链表
略
7.3.4多重链表
略
7.4图的遍历
7.4.1深度优先搜索遍历
图的深度优先搜索遍历类似于树的先序遍历,尽可能先对纵深方向进行搜索。其基本思想为从图中某个顶点V出发,访问此顶点,然后依次从V的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和V,有路径相通的顶点都被访问到。若图是连通图,则遍历过程结束,否则,图中还有顶点未被访问,则另选图中一个未被访问的顶点作
为新的出发点。重复上述过程,直至图中所有顶点都被访问到。
5-DFSAdjMatrix.c
#include<stdio.h>
#include "2-邻接矩阵plus.c" //去掉main()void visit(int v0){printf("%d ",v0);
}
//【算法 7-2】递归深度优先搜索遍历连通子图
int visited[MAXVEX]={0};//设置标志数组
//从v0出发递归地深度优先搜索遍历连通子图
void DFSAdjMatrix(AdjMatrix g,int v0){visit(v0);visited[v0]=1;int vj;//搜索图 if(g.t==1||g.t==2){for(vj=1;vj<=g.vexnum;vj++){if(visited[vj]==0&&g.arcs[v0][vj]==1) {DFSAdjMatrix(g,vj); }}} //搜索网if(g.t==3||g.t==4){for(vj=1;vj<=g.vexnum;vj++){if(visited[vj]==0&&g.arcs[v0][vj]!=INFINITY) {DFSAdjMatrix(g,vj); }}}
}
//【算法 7-3】深度优先遍历图g
void TraverseG(AdjMatrix g){int v;for(v=1;v<=g.vexnum;v++){visited[v]=0;}for(v=1;v<=g.vexnum;v++){if(!visited[v]){DFSAdjMatrix(g,v);}}
}
//int HasAPath(AdjMatrix g, int v, int w) {
// DFSAdjMatrix(g,v);
// if(visited[w]==1){
// return 1;
// }
// return 0;
//
//
//}typedef int ElemType;
#include "顺序栈.h"int FirstAdjVex(AdjMatrix g,int v){int null=INFINITY;int n=g.vexnum;int i=1;for(;i<=n;i++){if(g.arcs[v][i]!=null){break;}}if(i>n){return -1;} else{return i;} }
int NextAdjVex(AdjMatrix g,int v,int w){int null=INFINITY;int n=g.vexnum;int i=w+1;for(;i<=n;i++){if(g.arcs[v][i]!=null){break;}}if(i>n){return -1;} else{return i;} }
//【算法 7-4】非递归深度优先搜索遍历连通子图
//从v0出发递归地深度优先搜索遍历连通子图
void DFS(AdjMatrix g,int v0){SeqStack *S=InitStack();int visited[MAXVEX]={0};//访问标志数组Push(S,v0);while(!Empty(S)){int v;Pop(S,&v);if(!visited[v]){visit(v);visited[v]=1;}int w=FirstAdjVex(g,v);//图g中顶点v的第一个邻接点 while(w!=-1){if(!visited[w]){Push(S,w);}w=NextAdjVex(g,v,w);//图g中顶点v的下一个邻接点}}
} void main(){printf("创建\n");AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);int v0=1;printf("从v0=%d开始DFS:\n",v0); DFSAdjMatrix(*G,v0);printf("\n");printf("DFS:\n"); TraverseG(*G);printf("\n"); // visited[MAXVEX]={0};
// int r=HasAPath(*G,1,2);
// printf("%d",r);printf("非递归DFS:\n");DFS(*G,1);printf("\n"); printf("打印\n");Printf(G);
}
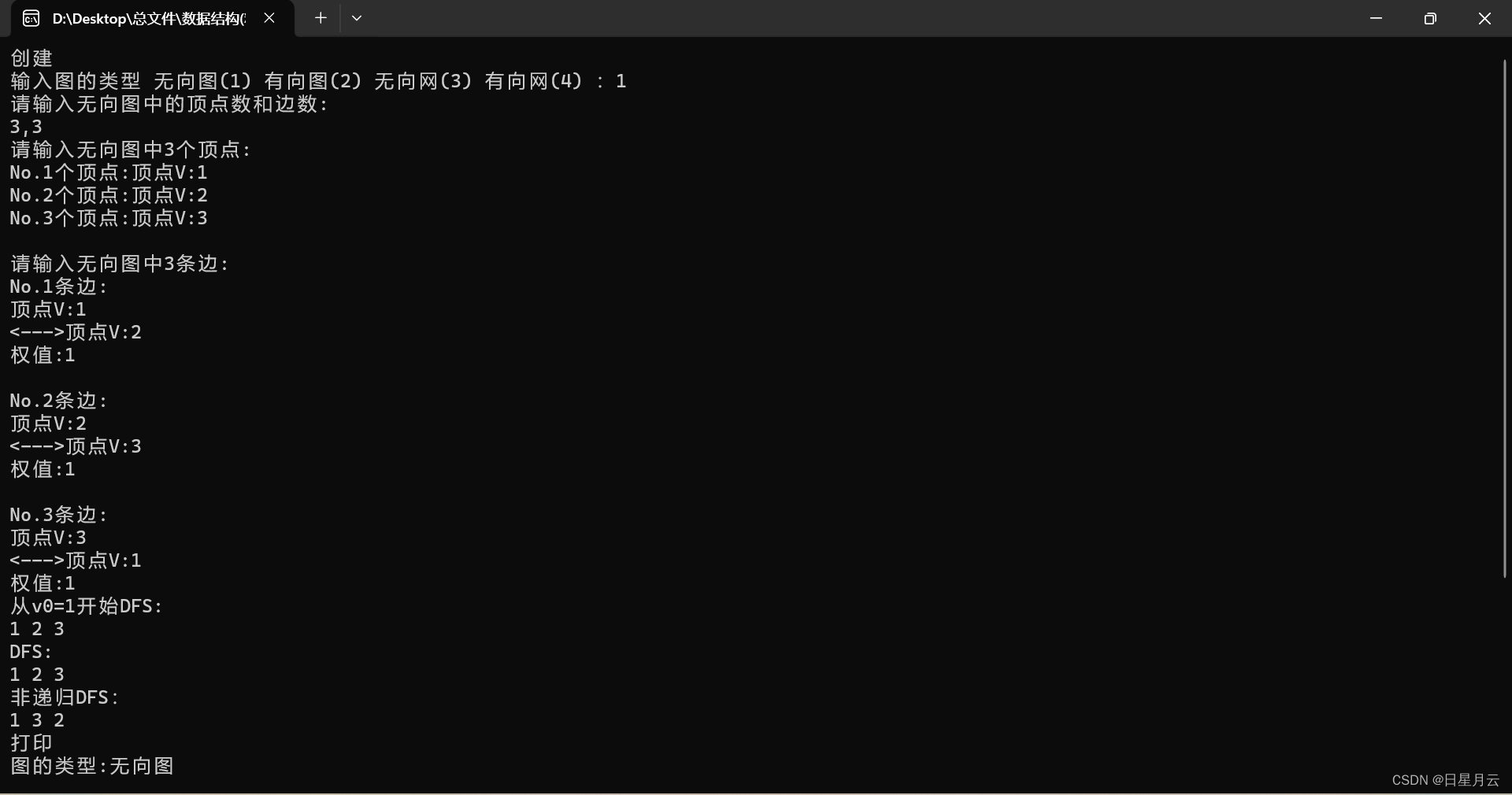
运行结果如下
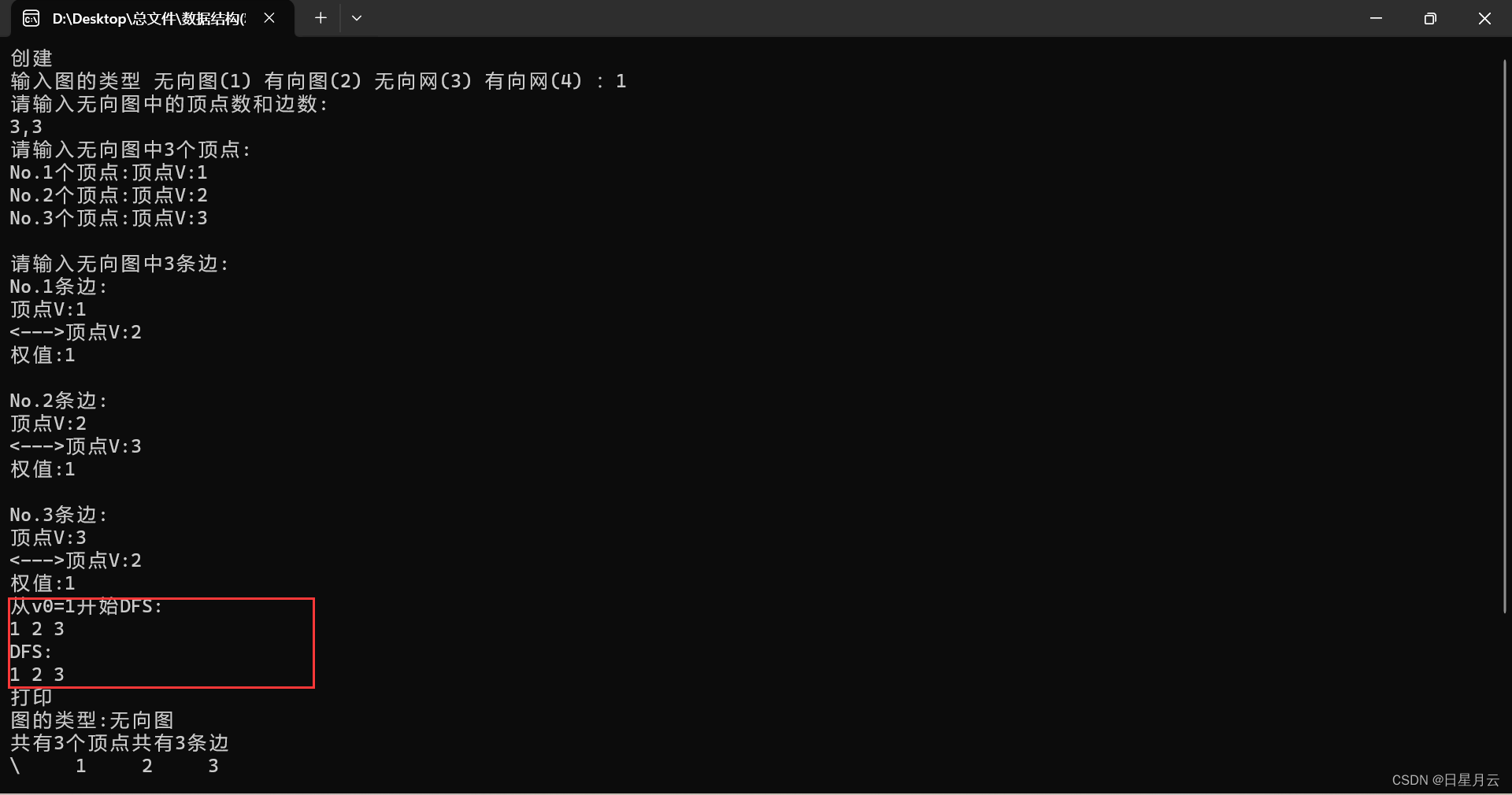
非递归DFS
6-DFSAdjList.c
#include<stdio.h>
#include "4-邻接表plus.c" //去掉main()
void visit(int v0){printf("%d ",v0);
} //【算法 7-2】递归深度优先搜索遍历连通子图int visited[MAXVEX]={0};//设置标志数组
//从v0出发递归地深度优先搜索遍历连通子图void DFSAdjList(AdjList g,int v0){visit(v0);visited[v0]=1;ArcNode* p=g.vertex[v0].head->next;while(p!=NULL){if(!visited[p->adjvex]){DFSAdjList(g,p->adjvex); }p=p->next;}
}
//【算法 7-3】深度优先遍历图g
void TraverseG(AdjList g){int v;for(v=1;v<=g.vexnum;v++){visited[v]=0;}for(v=1;v<=g.vexnum;v++){if(!visited[v]){DFSAdjList(g,v);}}
}typedef int ElemType;
#include "顺序栈.h"int FirstAdjVex(AdjList g,int v){ArcNode* h=g.vertex[v].head;ArcNode* p=h->next;if(p==NULL){return -1;}else{return p->adjvex;}}
int NextAdjVex(AdjList g,int v,int w){ArcNode* h=g.vertex[v].head;ArcNode* p=h->next;//找到之前的邻接点w while(p){if(p->adjvex==w){break;}p=p->next;}//找到w下一个邻接点p=p->next;if(p==NULL){return -1;}else{return p->adjvex;} }
//【算法 7-4】非递归深度优先搜索遍历连通子图
//从v0出发递归地深度优先搜索遍历连通子图
void DFS(AdjList g,int v0){SeqStack *S=InitStack();int visited[MAXVEX]={0};//访问标志数组Push(S,v0);while(!Empty(S)){int v;Pop(S,&v);if(!visited[v]){visit(v);visited[v]=1;}int w=FirstAdjVex(g,v);//图g中顶点v的第一个邻接点 while(w!=-1){if(!visited[w]){Push(S,w);}w=NextAdjVex(g,v,w);//图g中顶点v的下一个邻接点}}
} void main(){printf("创建\n");AdjList* G=(AdjList*)malloc(sizeof(AdjList));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("DFS:\n");
// int v0=1;
// DFSAdjMatrix(*G,v0);TraverseG(*G);printf("\n"); printf("非递归DFS:\n"); DFS(*G,1); printf("\n"); printf("打印\n");Printf(G);} 运行结果如下
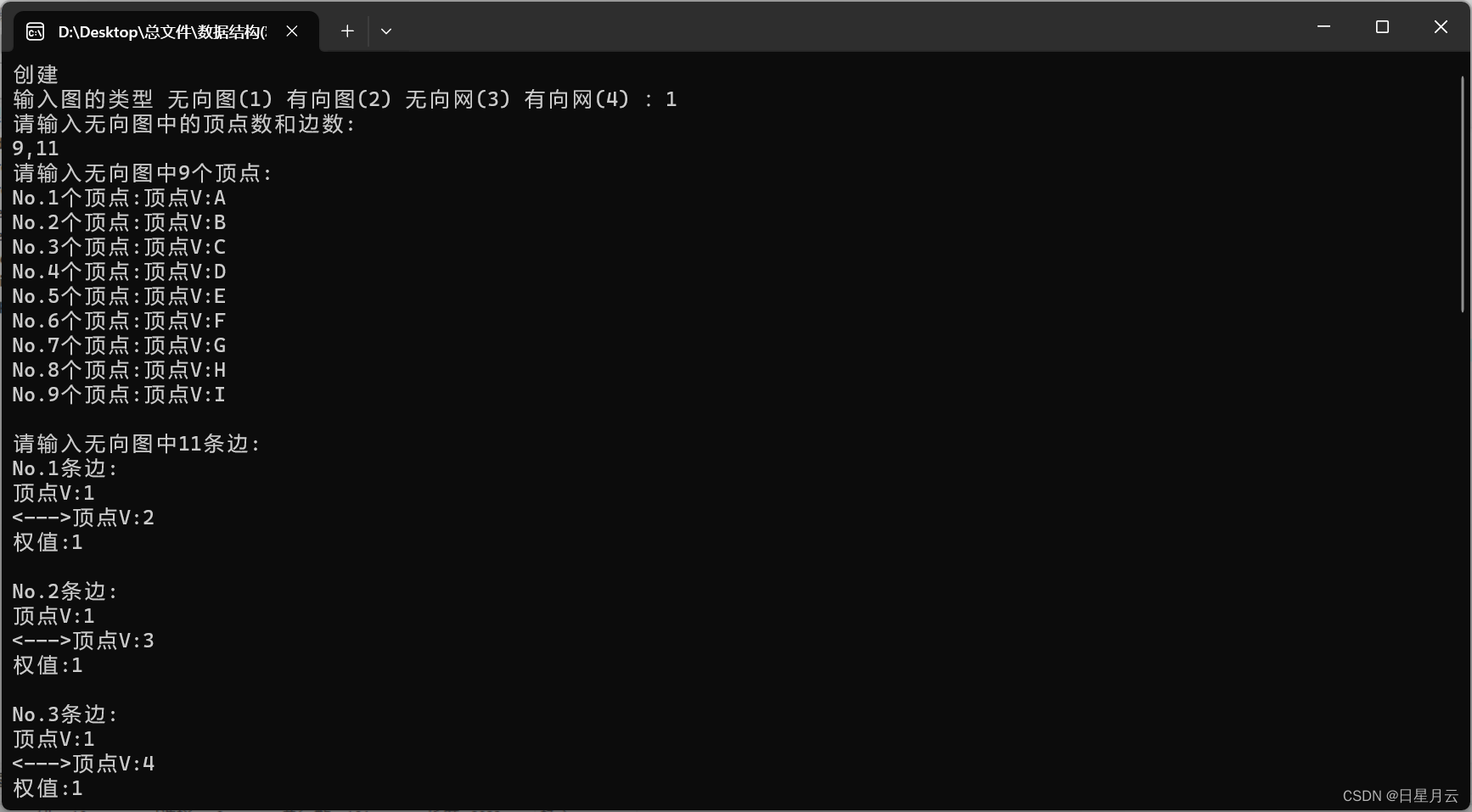
非递归DFS测试
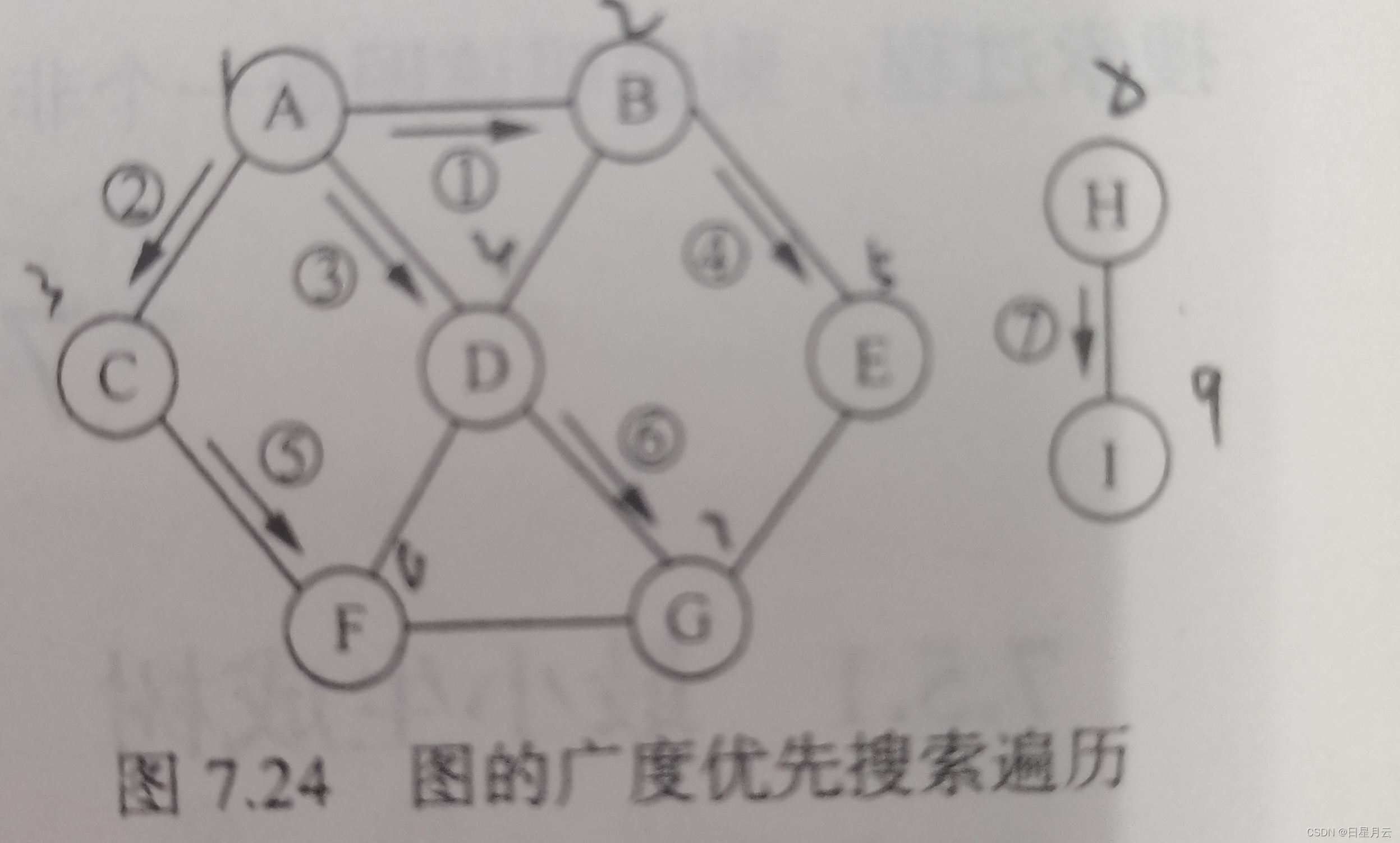
7.4.2广度优先搜索遍历
图的广度优先搜索遍历类似于树的按层次遍历,其基本思想为从图中的某个顶点V0出发,在访问此顶点之后依次访问V0。的所有未被访问的邻接点,之后按这些邻接点被访问的先后次序依次访问它们的邻接点,直至图中所有和V0有路径相通的顶点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未被访问的顶点作为新的出发点,重复上述过程,直至图中所有顶点都被访问到。
7-BFSAdjMatrix.c
#include<stdio.h>
#include "2-邻接矩阵plus.c" //去掉main()
#include "链队列.h" //去掉main()int visited[MAXVEX]={0};//设置标志数组
//从v0出发递归地深度优先搜索遍历连通子图
void visit(int v0){printf("%d ",v0);
}
//【算法7-5】广度优先搜索遍历连通子图
void BFSAdjMatrix(AdjMatrix g,int v0){int v; visit(v0);visited[v0]=1;LQueue *Q=Init_LQueue();InLQueue(Q,v0);//入队int vj; while(!Empty_LQueue(Q)){Out_LQueue(Q,&v);//出队//搜索图 if(g.t==1||g.t==2){for(vj=1;vj<=g.vexnum;vj++){if(visited[vj]==0&&g.arcs[v][vj]==1) {visit(vj);visited[vj]=1;InLQueue(Q,vj);}}} //搜索网if(g.t==3||g.t==4){for(vj=1;vj<=g.vexnum;vj++){if(visited[vj]==0&&g.arcs[v][vj]!=INFINITY) {visit(vj);visited[vj]=1;InLQueue(Q,vj); }}} } }
//【算法7-6】广度优先遍历图g
void TraverseG(AdjMatrix g){int v;for(v=1;v<=g.vexnum;v++){visited[v]=0;}for(v=1;v<=g.vexnum;v++){if(!visited[v]){BFSAdjMatrix(g,v);}}
}void main(){printf("创建\n");AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("BFS:\n");
// int v0=1;
// BFSAdjMatrix(*G,v0);TraverseG(*G);printf("\n"); printf("打印\n");Printf(G);}
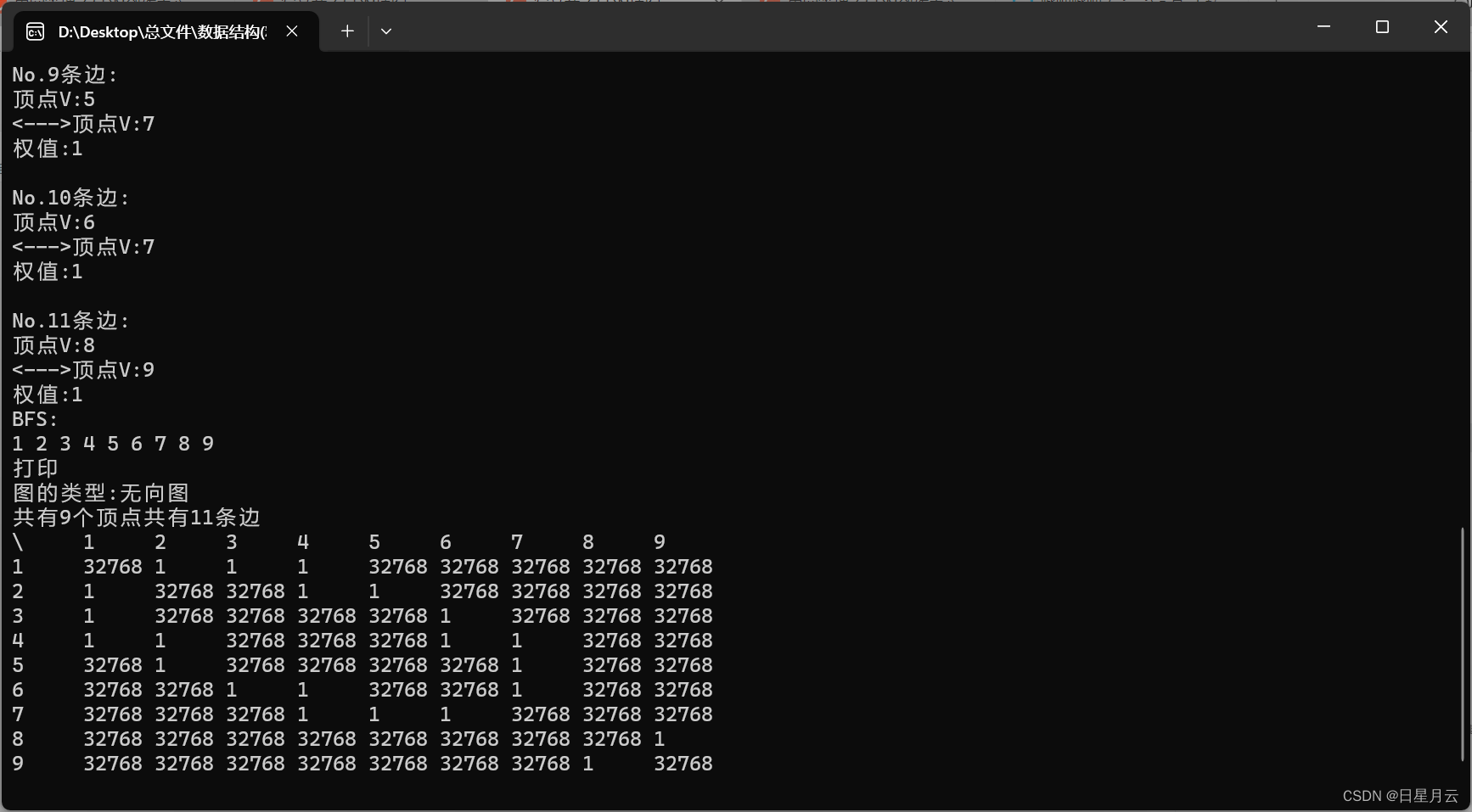
8-BFSAdjList.c
#include<stdio.h>
#include "4-邻接表plus.c"
#include "链队列.h" int visited[MAXVEX]={0};//设置标志数组
//从v0出发递归地深度优先搜索遍历连通子图
void visit(int v0){printf("%d ",v0);
}
//【算法 7-5】广度优先搜索遍历连通子图
void BFSAdjList(AdjList g,int v0){visit(v0);visited[v0]=1;LQueue *Q=Init_LQueue();InLQueue(Q,v0);//入队int v;while(!Empty_LQueue(Q)){Out_LQueue(Q,&v);//出队ArcNode* p=g.vertex[v].head->next;if(!visited[p->adjvex]){visit(p->adjvex);visited[p->adjvex]=1;}p=p->next;}
}
//【算法7-6】广度优先遍历图g
void TraverseG(AdjList g){int v;for(v=1;v<=g.vexnum;v++){visited[v]=0;}for(v=1;v<=g.vexnum;v++){if(!visited[v]){BFSAdjList(g,v);}}
}void main(){printf("创建\n");AdjList* G=(AdjList*)malloc(sizeof(AdjList));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("BFS:\n");
// int v0=1;
// BFSAdjList(*G,v0);TraverseG(*G);printf("\n"); printf("打印\n");Printf(G);}
运行结果如下
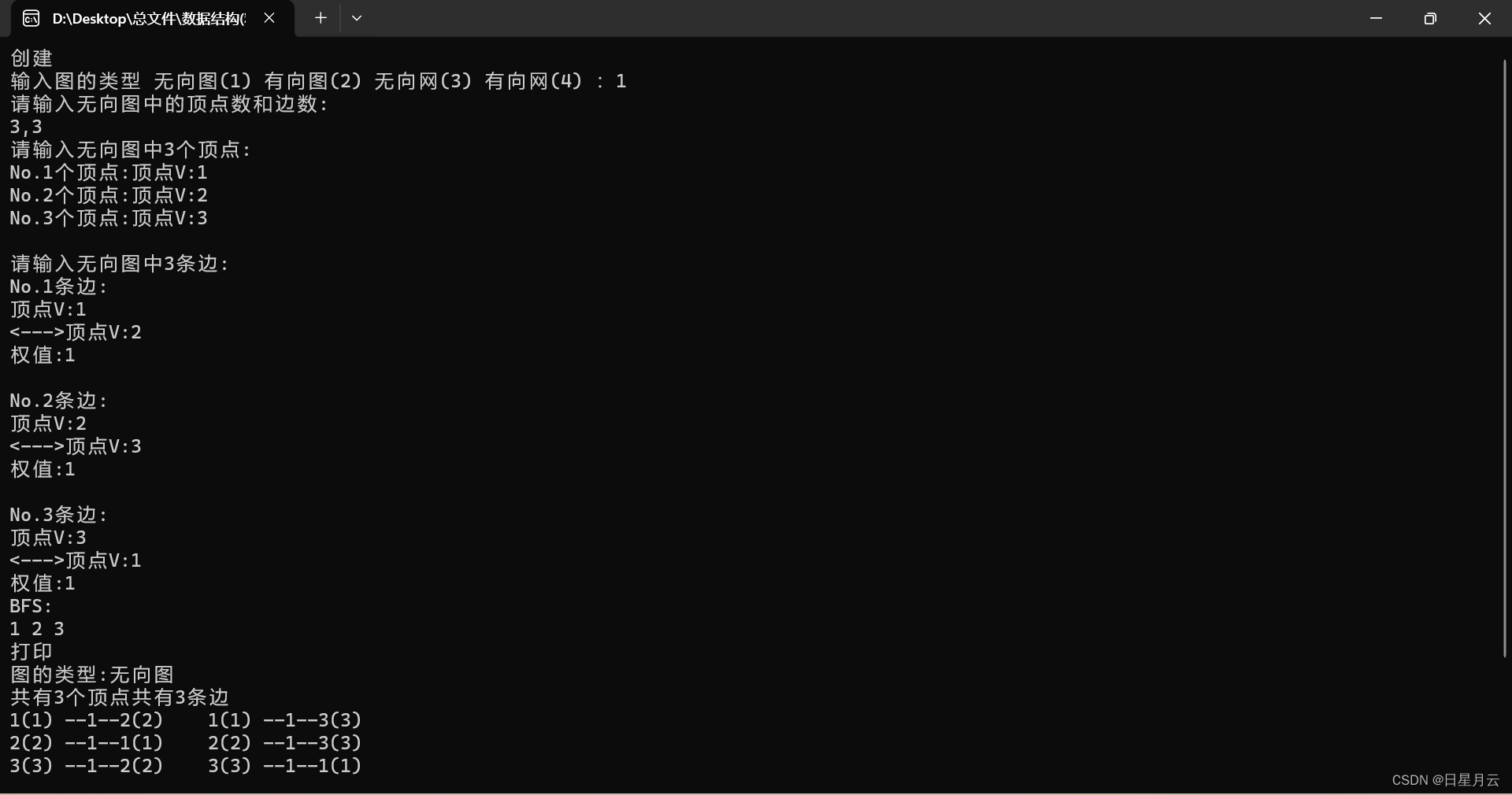
7.5图的应用
7.5.1最小生成树
图G的生成树是指该图的一个极小连通子图,含有图中的全部n个顶点,但只有足以构成
棵树的n-1条边。显然,生成树不唯一,可能有多棵。
在一个连通网的所有生成树中,选中的n-1条边权值(代价)之和最小的生成树被称为该连通网的“最小代价生成树"(minimum-cost spanning tree,MST)。
MST性质:设图G=<V,R>是一个带权的连通图,即连通网,集合U是顶点集V的一个非空
子集。构建生成树时需要一条边连通顶点集合U和V-U。如果(u,v)∈R,其中,u∈U,v∈V-U,且边(u,v)是具有最小权值的一条边,那么一定存在一棵包含边(u,v)的最小生成树。
1.Prim算法(加点法)
适用于稠密图
基本思想:从连通网络N={v,E}中的某一顶点u出发,选择与它关联的具有最小权值的边(u0,v),将其顶点加人生成树的顶点集合U。以后每一步从一个顶点在U中,而另一个顶点不在U中的各条边中选择权值最小的边(u,v),把它的顶点加人集合U中,这意味着(u,v)也加入生成树的边集合。如此继续下去,直到网络中的所有顶点都加入生成树的顶点集合U中为止。
具体地,记N是连通网的顶点集,U是求得生成树的顶点集,TE是求得生成树的边集
①开始时,U={U0}TE=∅。
②修正U到其余顶点N-U的最小权值,将具有最小权值的边纳入TE,对应的顶点纳入U。
③重复②直到U=N。
经过上述步骤,TE中包含了G中的n-1条边,此时选取到的所有顶点及边恰好就构成了G的一棵最小生成树。
9-Prim.c
#include<stdio.h>
#include "2-邻接矩阵plus.c"
typedef int VertexData;
int LocateVertex(AdjMatrix gn,VertexData u){int i;for(i=1;i<=gn.vexnum;i++){if(gn.vex[i]==u){return i;}}
}//【7-7】Prim算法求得最小生成树
void Prim(AdjMatrix gn,VertexData u){struct{int adjvex;int lowcost;}closedge[MAXVEX];int k;k=LocateVertex(gn,u);closedge[k].lowcost=0;int i;for(i=1;i<=gn.vexnum;i++){if(i!=k){closedge[i].adjvex=u;closedge[i].lowcost=gn.arcs[k][i];}}int k0,u0,v0,e;for(e=1;e<=gn.vexnum-1;e++){//选择最小权值的边 int m,min=INFINITY;for(k=1;k<=gn.vexnum;k++){if(closedge[k].lowcost!=0&&closedge[k].lowcost<min){m=k;min=closedge[k].lowcost;}}
// k0=Minium(closedge);k0=m;u0=closedge[k0].adjvex;v0=gn.vex[k0];printf("第%d条边:%d--%d--%d\n ",e,u0,min,v0);closedge[k0].lowcost=0;for(i=1;i<=gn.vexnum;i++){if(gn.arcs[k0][i]<closedge[i].lowcost){closedge[i].lowcost=gn.arcs[k0][i];closedge[i].adjvex=v0;}}}
}int main(){printf("创建\n");AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("最小生成树\n");VertexData u=1;Prim(*G,u);printf("打印\n");Printf(G);
}
运行结果如下
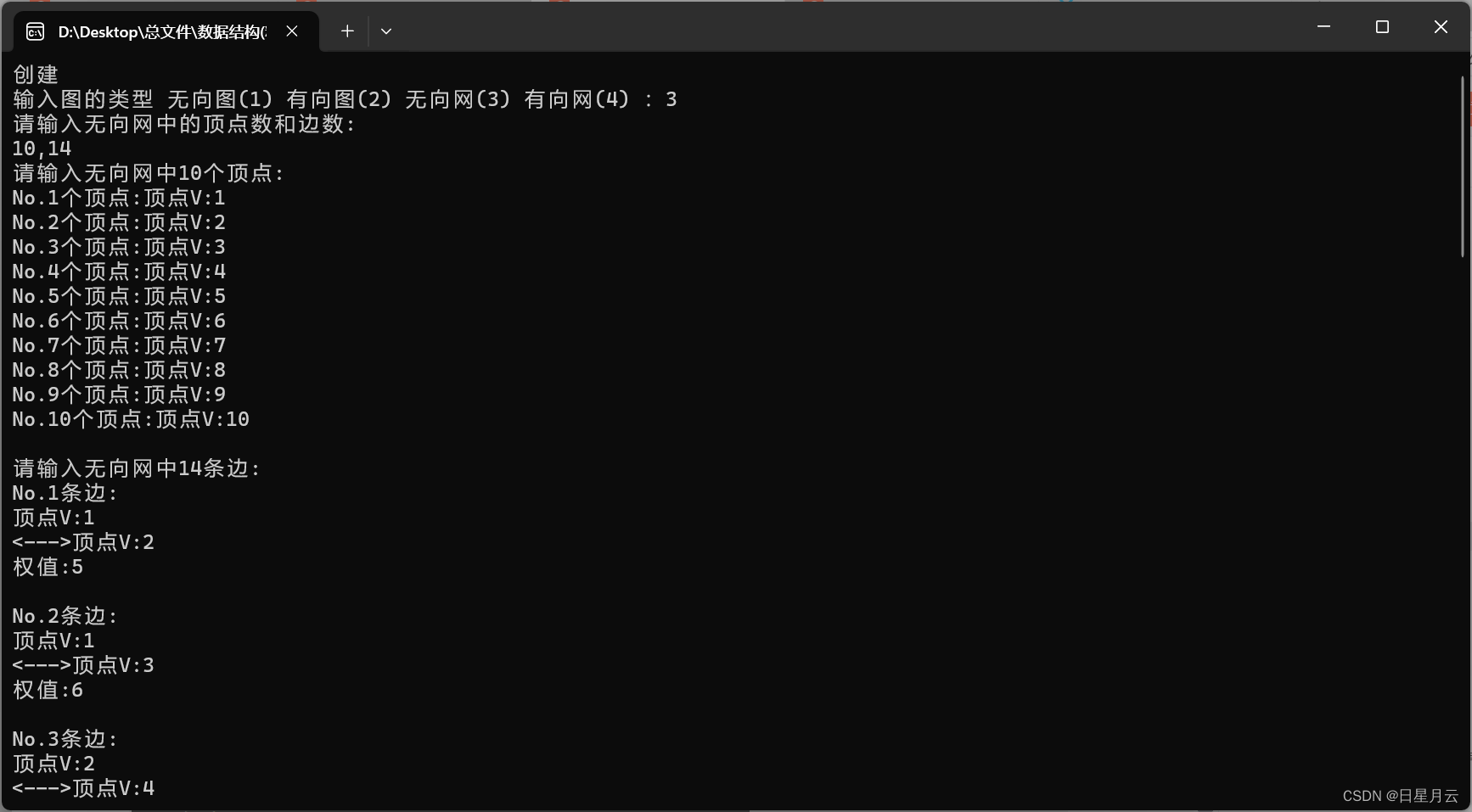

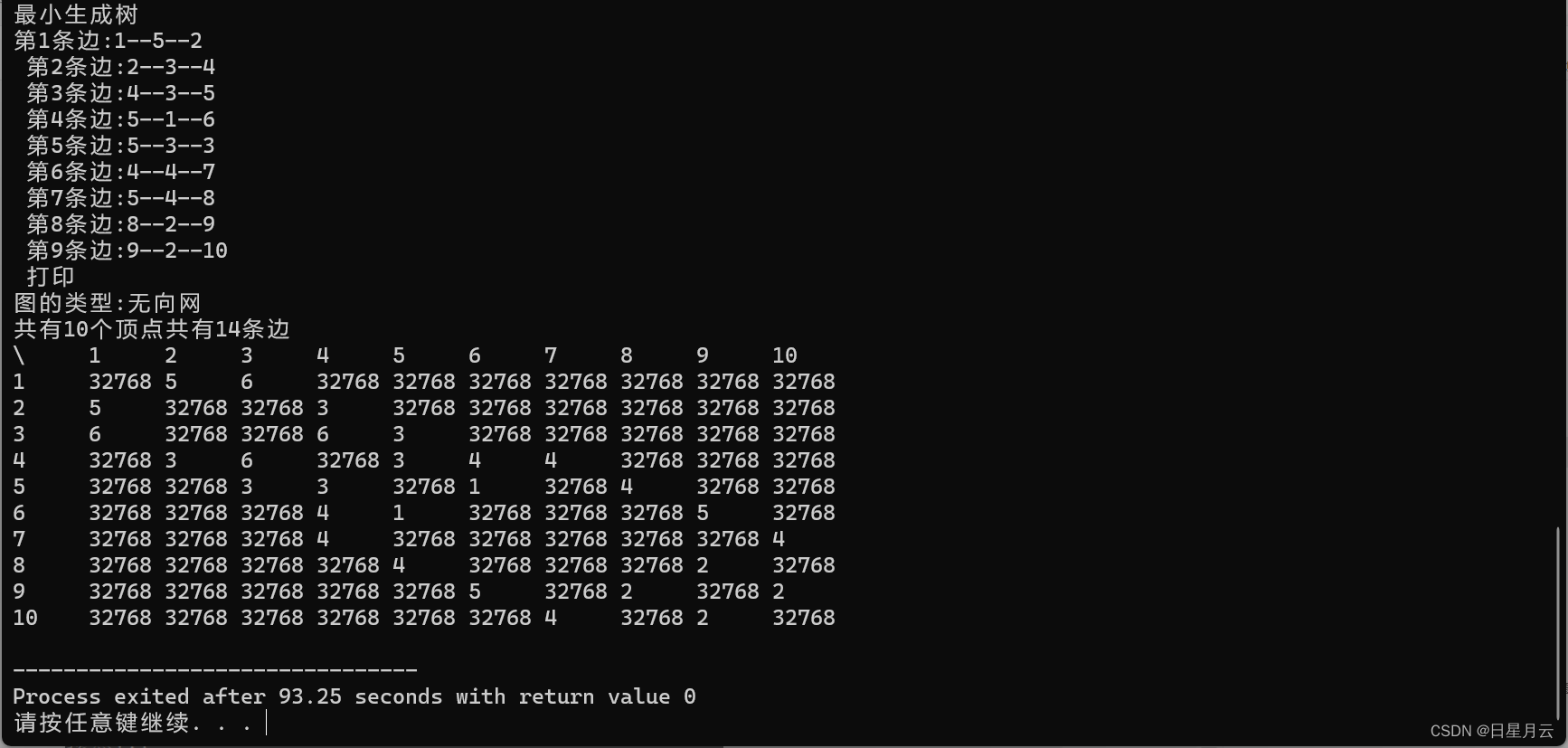
说明
最小生成树
每两个代表生成树一个边的两个顶点
4 7 可以改成7 10也是对的
2.Kruskal算法(加边法)
适用于稀疏图
Kruskal算法使用的贪心准则是,从剩下的边中选择不会产生环路且具最小权值的边加人生成树的边集。
基本思想:先构造一个只含n个顶点的子图SG,然后从权值最小的边
开始,若它的添加不使SG中产生回路,则在SG上加入该边,依次按照权值通增的次序,选择合适的边进行添加,如此重复,直至加完n-1条边为止。
7.5.2 拓扑排序
假设以有向图表示个工程的施工图或程序的数据流图,每个顶点代表一个活动,弧<vi,vj)表示活动必须先于活动j进行。我们将顶点表示活动、弧表示活动间优先关系的有向无“顶点表示活动的网”,简称"AOV-网"(activity on vertex),图中不允许出现回路。
对于一个AOV-网,若存在满足以下性质的一个线性序列,则这个线性序列称为“拓扑序列”。
①网中的所有顶点都在该序列中。
②若顶点i到顶点Vj存在一条路径,则在线性序列中,Vi一定排在Vj之前。
构造拓扑序列的操作称为“拓扑排序”。实际上,拓扑排序就是离散数学中由某个集合上一个偏序得到该集合上的一个全序的操作。
那么,对于一个AOV-网来说,如何求得拓扑序列呢?其方法如下。
①从有向图中选取一个没有前驱的顶点并输出之。
②从有向图中删去该顶点以及所有以它为尾的弧。
③重复上述两步,直至图空(不存在回路),或者图不空但找不到无前驱的顶点为止(存在 回路)。可见,拓扑排序可以检查有向图中是否存在回路。
相关代码请看配套资源
10-拓扑排序.c
#include<stdio.h>
#include<stdlib.h>
#include "4-邻接表plus.c"
#include "链队列.h"//【算法7-8】获取图中每个顶点入度值】
void FindID(AdjList G, int indegree[MAXVEX]) {// 格个顶点的人度值int i;ArcNode *p;for(i=1;i<=G.vexnum;i++){indegree[i]=0; //初始化indegree数组 }for(i=1;i<=G.vexnum;i++){p=G.vertex[i].head->next; while(p!=NULL){indegree[p->adjvex]++; p=p->next;}}
}//【算法7-9】 拓扑排序
int TopoSort (AdjList G){LQueue *Q;/*队列*/int indegree[MAXVEX]={0};int i, count, k;ArcNode *p;FindID(G,indegree);Q=Init_LQueue();for(i=1;i<=G.vexnum;i++){if(indegree[i]==0){InLQueue(Q,i);}} count=0;while(!Empty_LQueue(Q)){Out_LQueue(Q,&i);printf("%c ",G.vertex[i].vexdata); count++;p=G.vertex[i].head->next;while(p!=NULL){k=p->adjvex;indegree[k]--;if(indegree[k]==0) {InLQueue(Q,k); }p=p->next;}}if (count<G.vexnum) return 0;else return 1;}void main(){AdjList* G=(AdjList*)malloc(sizeof(AdjList));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("\n"); printf("拓扑排序");
// int indegree[MAXVEX];
// FindID(*G,indegree);
// int i;
// for(i=1;i<=G->vexnum;i++){
// printf("%d ",indegree[i]);
// }TopoSort(*G);printf("\n");Printf(G);
}
运行结果如下


7.5.3关键路径
略
7.5.4最短路径
1.单元最短路径
DIjkstra算法
11-单源最短路径.c
#include<stdio.h>
#include<stdlib.h>
#include "2-邻接矩阵plus.c"
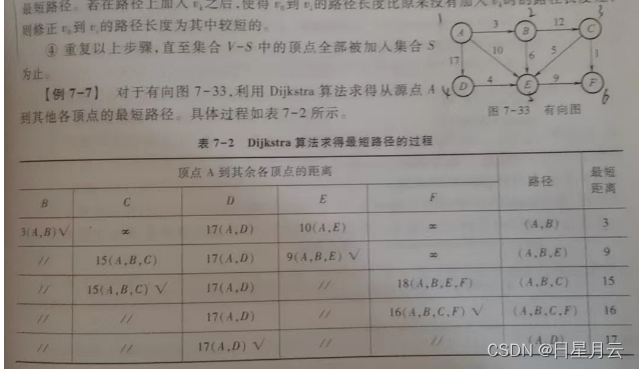
//【算法7-11】采用Dijkstra算法求得从源点到其余各顶点的最短路径
void Dijkstra(AdjMatrix *G,int start,int end,int dist[],int path[][MAXVEX]){//dist数组记录各条最短路径长度,path数组记录对应路径上的各顶点 int mindist,i,j,k,t=1;for(i=1;i<=G->vexnum;i++){ //初始化dist[i]=G->arcs[start][i];if(G->arcs[start][i]!=INFINITY){ path[i][1]=start;} } path[start][0]=1;for(i=2;i<=G->vexnum;i++){ //寻找各条最短路径mindist=INFINITY;for(j=1;j<=G->vexnum;j++) { //选择最小权值的路径 if(!path[j][0]&&dist[j]<mindist){ k=j;mindist=dist[j];}} if(mindist==INFINITY) return;path[k][0]=1;for(j=1;j<=G->vexnum;j++){ //修改路径 if(!path[j][0]&&G->arcs[k][j]<INFINITY&&dist[k]+ G->arcs[k][j]<dist[j]){dist[j]=dist[k]+G->arcs[k][j];t=1;while(path[k][t]!=0){ //记录最新的最短路径 path[j][t]=path[k][t];//伪代码 t++;} path[j][t]=k;path[j][t+1]=0;} }}}
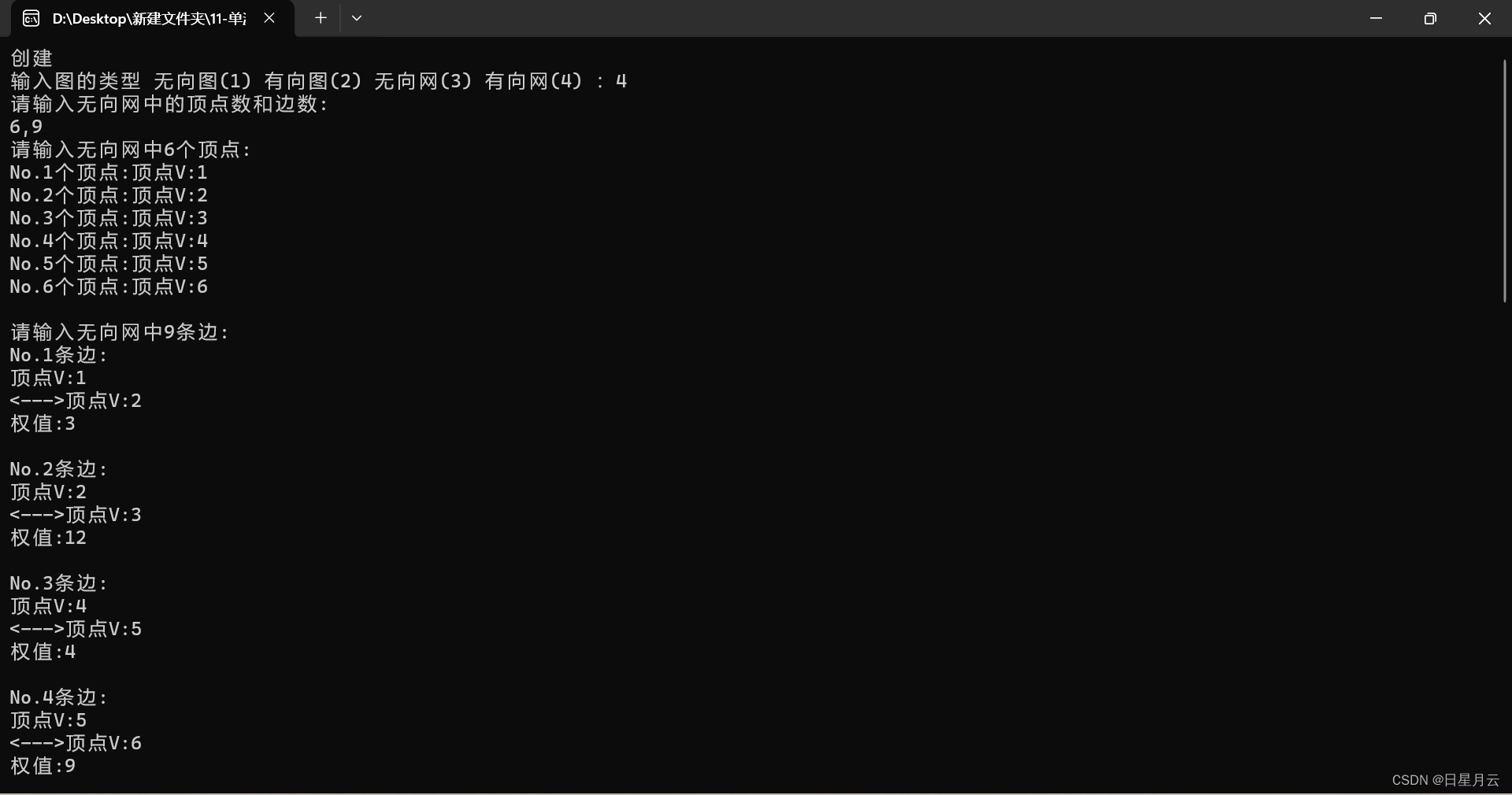
void printPath(AdjMatrix *G,int start,int end,int dist[],int path[][MAXVEX]){int i,j;printf("从%d到其余顶点\n",start);for(i=1;i<=G->vexnum;i++){ if(i==start){printf("到本身顶点%d的最短路径长度为0\n",i);}else{
// if(path[i][0]==1){printf("到顶点%d的最短路径长度为%d\n",i,dist[i]);printf("其路径为:"); j=1;while(path[i][j]!=0) {printf("%d ",path[i][j]);j++;}printf("\n");
// }else{
// printf("无路径\n");
// }} }
}
void main(){printf("创建\n");AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("\n");int start=1;int end=2;int dist[G->vexnum+1];int path[G->vexnum+1][MAXVEX];Dijkstra(G,start,end,dist,path); printPath(G,start,end,dist,path);printf("打印\n");Printf(G);
}
运行结果

2.每对顶点之间的路径
Floyd算法
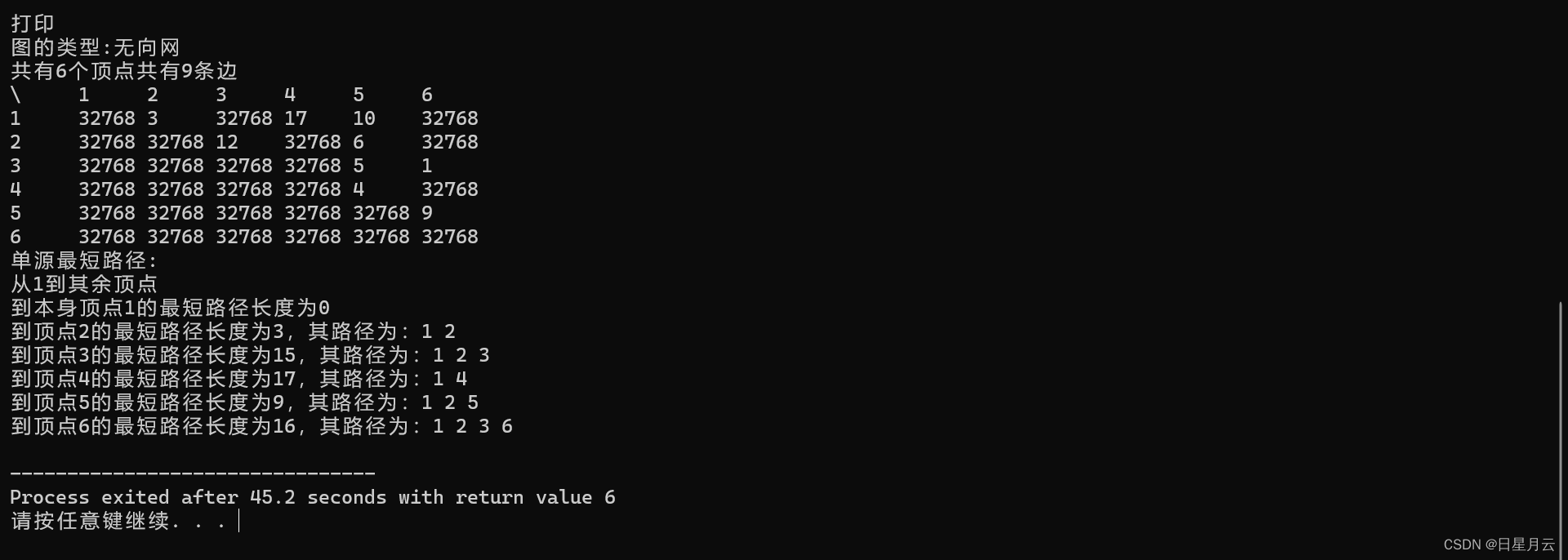
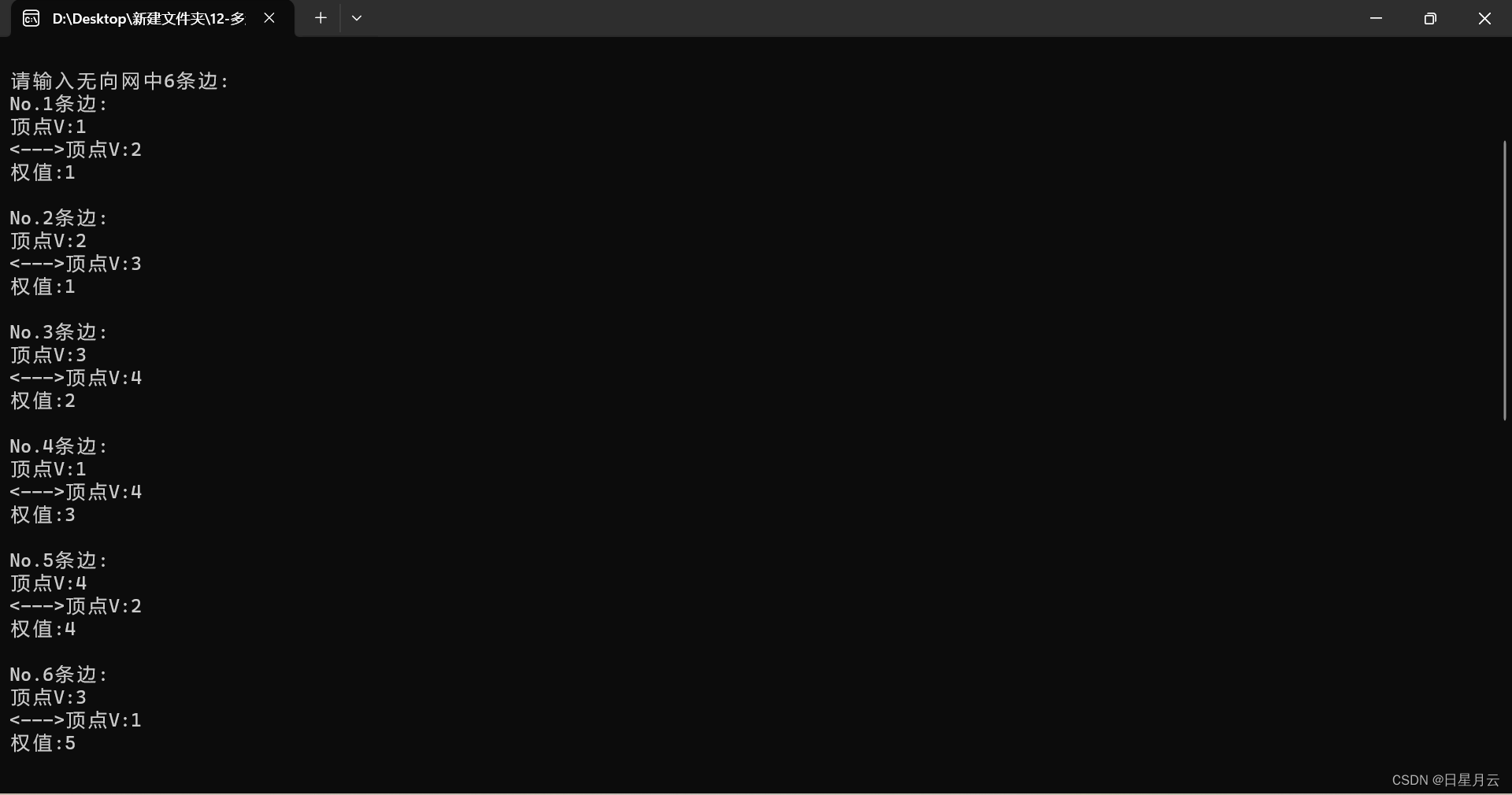
12-多源最短路径.c
#include<stdio.h>
#include<stdlib.h>
#include "2-邻接矩阵plus.c" void printFP(int n,int F[][MAXVEX],int Path[MAXVEX][MAXVEX]){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j){printf("0\t");}else{printf("%d\t",F[i][j]);}}printf("\n");}
// for (int i = 1; i <= n; i++) {
// for (int j = 1; j <= n; j++) {
// printf("%d\t",Path[i][j]);
// }
// printf("\n");
// }
}//【算法7-12】Floyd算法求得任意两顶点之间的最短路径
void Floyd(AdjMatrix g,int F[][MAXVEX],int Path[][MAXVEX]){int i,j,k;for(i=1;i<=g.vexnum;i++){for(j=1;j<=g.vexnum;j++) {F[i][j]=g.arcs[i][j];
// if (F[i][j] != INFINITY) {
// Path[i][j] = j; // 如果i和j之间有边,则Path[i][j]为j
// } else {
// Path[i][j] = -1; // 如果i和j之间没有边,则Path[i][j]为-1
// }}} for(i=1;i<=g.vexnum;i++){ for(j=1;j<=g.vexnum;j++) { for(k=1;k<=g.vexnum;k++){ if(F[i][j]>F[i][k]+F[k][j]){F[i][j]=F[i][k]+F[k][j];
// Path[i][j] = Path[i][k]; // 更新Path[i][j]为经过顶点k的路径}}}}}//void printPath(int i, int j, int Path[][MAXVEX]) {
// if (Path[i][j] == -1) {
// printf("%d ", i);
// } else {
// printPath(i, Path[i][j], Path);
// printf("%d ", j);
// }
//}void main(){printf("创建\n");AdjMatrix* G=(AdjMatrix*)malloc(sizeof(AdjMatrix));printf("输入图的类型 ");printf("无向图(1) ");printf("有向图(2) ");printf("无向网(3) ");printf("有向网(4) :");scanf("%d",&G->t); Create(G);printf("\n");printf("打印\n");Printf(G);printf("多源最短路径\n"); int n=G->vexnum;int F[n][n];int Path[n][n];Floyd(*G,F,Path);printFP(n,F,Path);// for (int i = 1; i <= n; i++) {
// for (int j = 1; j <= n; j++) {
// if (i != j) {
// printf("从顶点 %d 到顶点 %d 的最短路径为:", i, j);
// printPath(i, j, Path);
// printf("\n");
// }
// }
// }
}
运行结果



6实例分析与实现
略
7算法总结 贪心算法
略
习题7
3完成题 1 2 4 6
(1)对于图7-37所示的有向网:
①给出该图对应的邻接矩阵、邻接表和逆邻接表
②判断该图是否为强连通图,并给出其强连通分量
③给出每个顶点的度、人度和出度
④给出从顶点V,开始的深度优先搜索遍历序列和广度优先搜索遍历序列
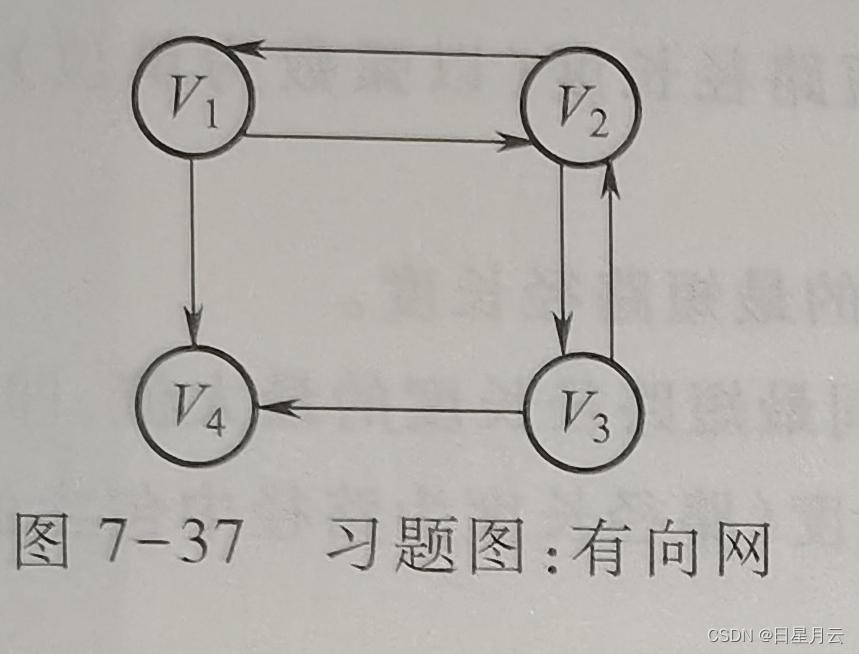
略
(2)如图7-38所示的无向网,请给出分别按Prim(从顶点V1开始)和Kruskal算法构造的最小生成树并给出构造过程。
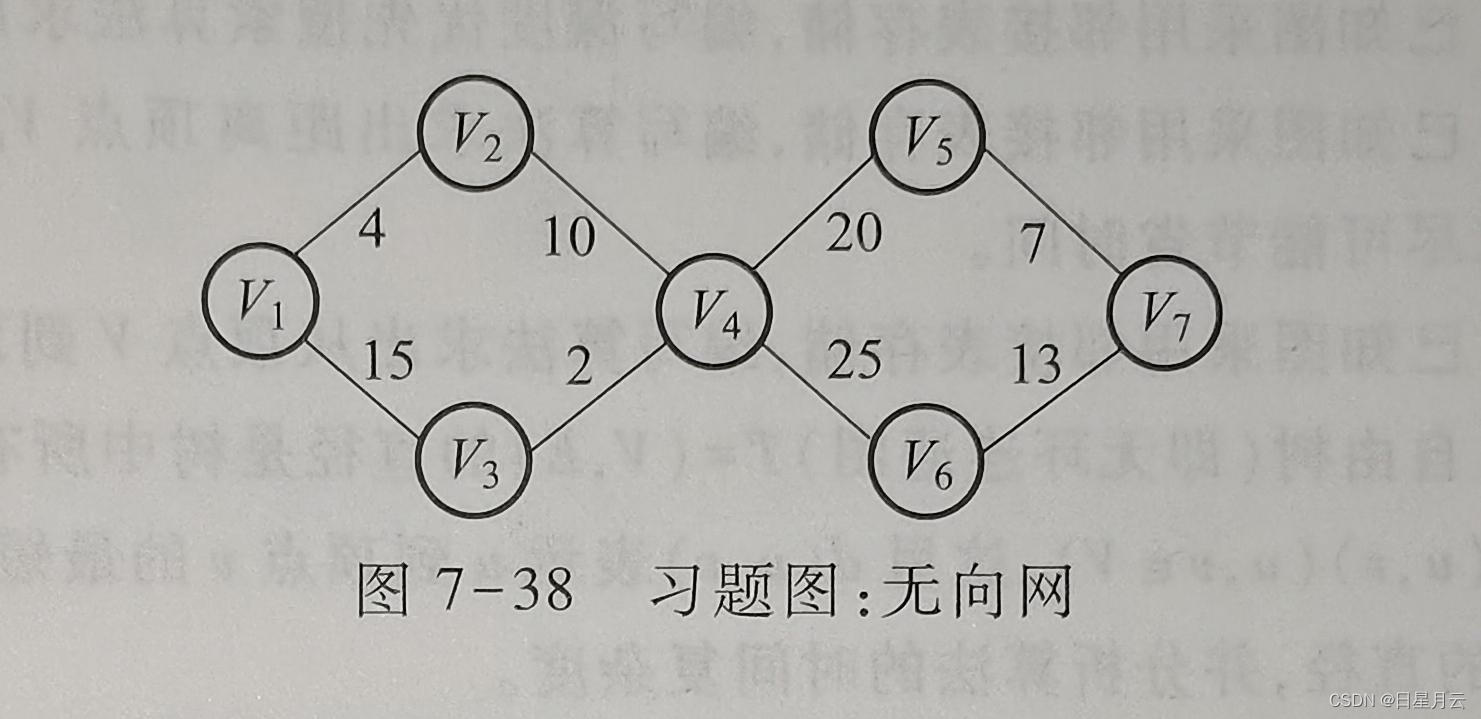
略
(4)如图7-40所示的有向网,利用Dijkstra算法求顶点V0到其他各顶点之间的最短路径以及最短路径长度
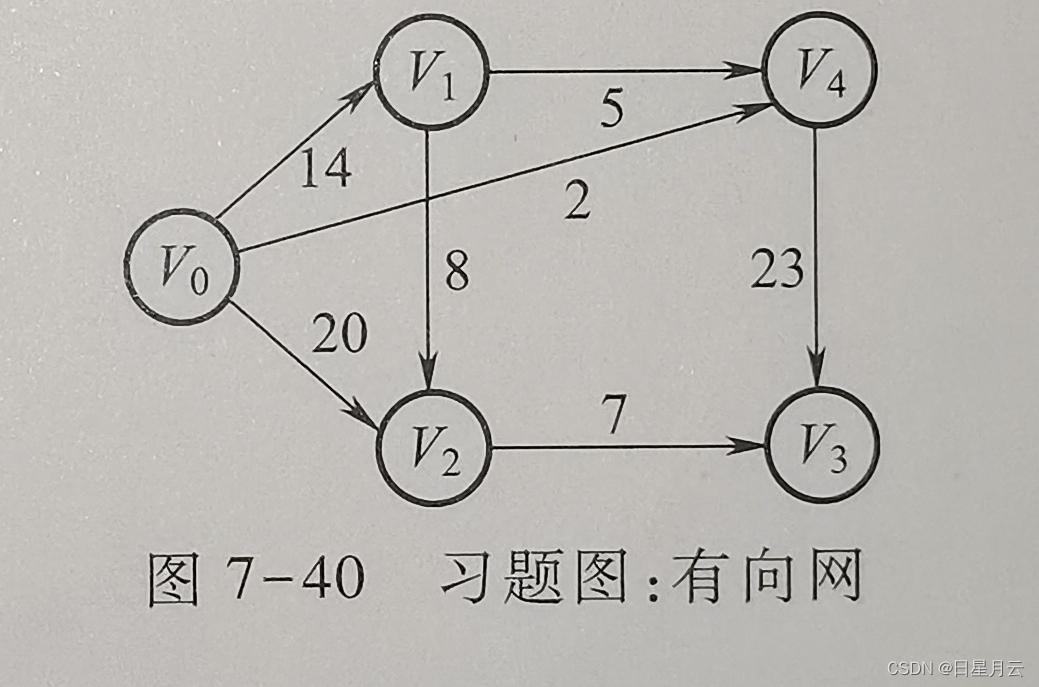
略
(6)对如图7-42所示的有向图进行拓扑排序,写出可能的3种拓扑序列。
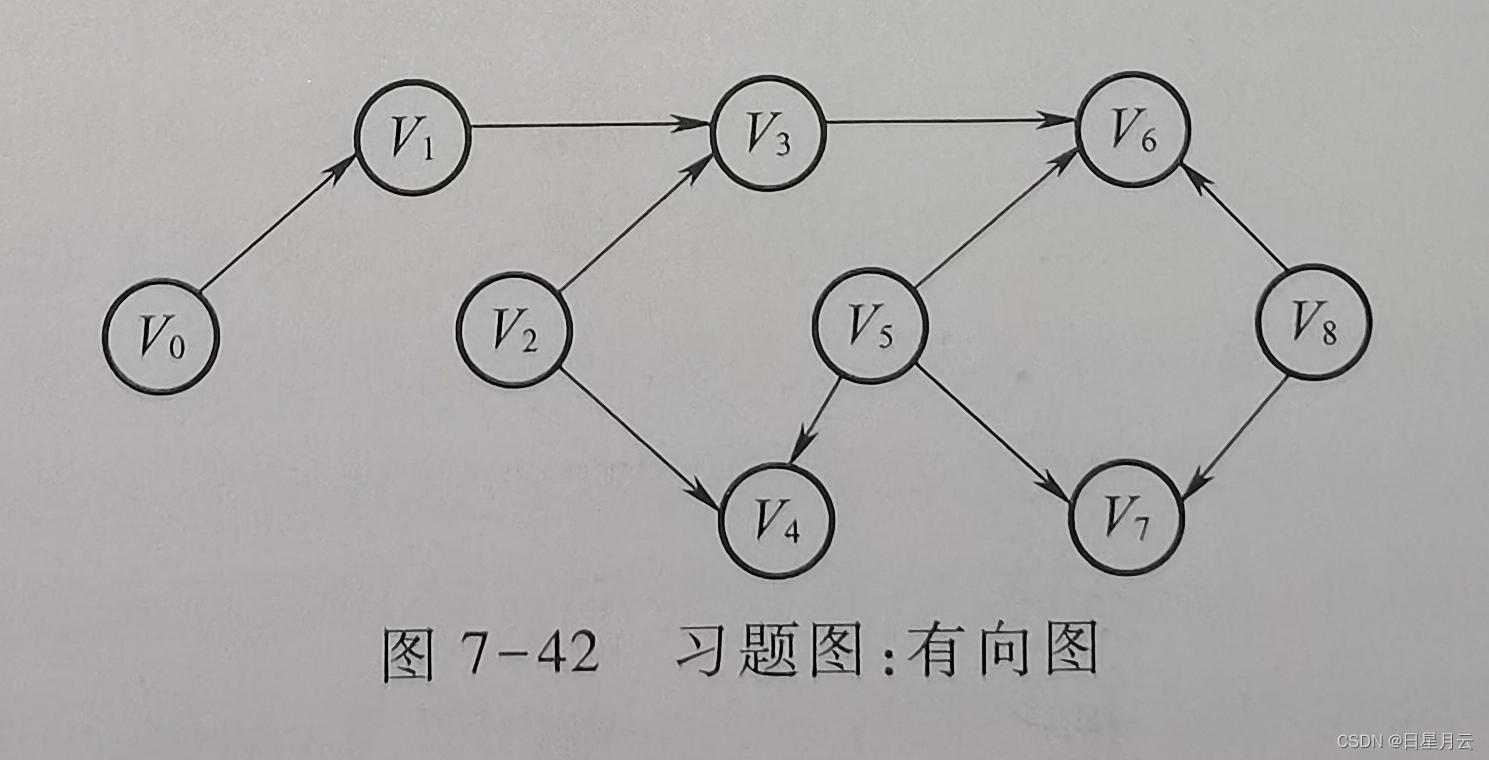
略
4.算法设计题
(11)已知有向图以邻接表作为存储结构,编写算法判断该图中是否存在顶点Vi到顶点Vj,的简单路径,并输出该路径上的顶点。
略
最后
2023-11-6 17:51:52
2023-11-7 16:00:47
我们都有光明的未来
不必感谢我,也不必记得我
祝大家考研上岸
祝大家工作顺利
祝大家得偿所愿
祝大家如愿以偿
点赞收藏关注哦
相关文章:

第七章 图【数据结构与算法】【精致版】
第七章 图【数据结构与算法】【精致版】 前言版权第七章 图7.1 应用实例7.2图的基本概念7.3图的存储结构7.3.1邻接矩阵**1-邻接矩阵.c****2-邻接矩阵plus.c** 7.3.2 邻接表**3-邻接表.c** **4-邻接表plus.c** 7.3.3 十字链表7.3.4多重链表 7.4图的遍历7.4.1深度优先搜索遍历**5…...

模型蒸馏学习
知识蒸馏:获取学生网络和教师网络指定蒸馏位点的输出特征并计算蒸馏 loss 的过程 知乎-mmrazor-模型蒸馏 知识蒸馏算法往往分为 reponse-based基于响应、feature-based基于特征 和 relation-based基于关系三类。 也可为 data-free KD、online KD、self KDÿ…...

总结Kibana DevTools如何操作elasticsearch的常用语句
一、操作es的工具 ElasticSearch HeadKibana DevToolsElasticHQ 本文主要是总结Kibana DevTools操作es的语句。 二、搜索文档 1、根据ID查询单个记录 GET /course_idx/_doc/course:202、term 匹配"name"字段的值为"6789999"的文档 类似于sql语句中的等…...

【QT】QT自定义C++类
在使用Qt的ui设计时,Qt为我们提供了标准的类,但是在很多复杂工程中,标准的类并不能满足所有的需求,这时就需要我们自定义C类。 下面以自定义的QPushButton作一个很简单的例子。 先新建默认Qt Widgets Application项目 一、自定义…...

【多媒体文件格式】AVI、WAV、RIFF
AVI、RIFF AVI:Audio/Video Interleaved(音频视频交织/交错),用于采集、编辑、播放的RIFF文件。由Microsoft公司1992年11月推出,是Microsoft公司开发的一种符合RIFF文件规范的数字音频与视频文件格式,原先…...
AI创作系统ChatGPT商业运营系统源码+支持GPT4/支持ai绘画
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...

JWT简介 JWT结构 JWT示例 前端添加JWT令牌功能 后端程序
目录 1. JWT简述 1.1 什么是JWT 1.2 为什么使用JWT 1.3 JWT结构 1.4 验证过程 2. JWT示例 2.1 后台程序 2.2 前台加入jwt令牌功能 1. JWT简述 1.1 什么是JWT Json web token (JWT), 是为了在网络应用环境间传递声明而执行的一种基于JSON的开放标准((RFC 7…...
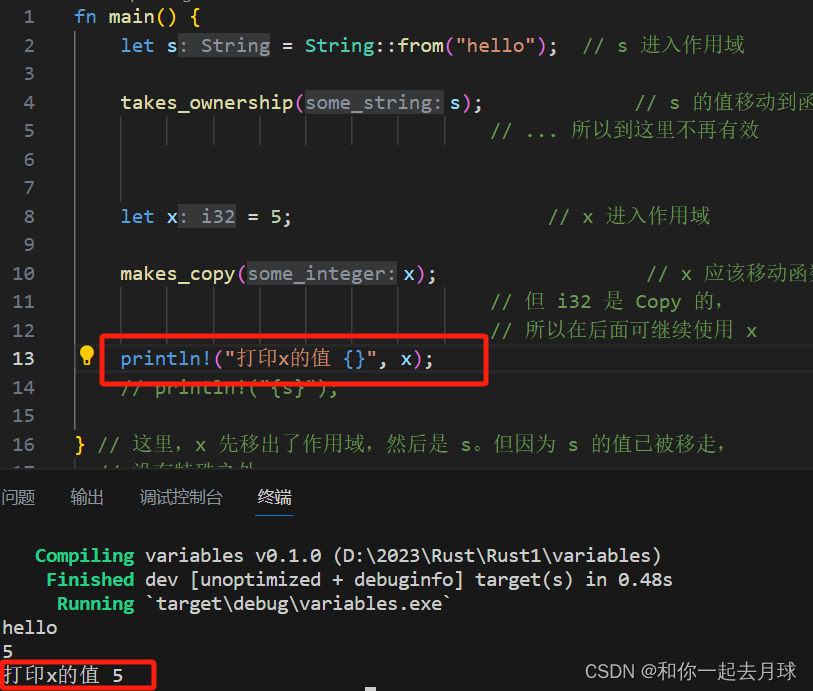
Rust核心功能之一(所有权)
目录 1、什么是所有权? 1.1 所有权规则 1.2 变量作用域 1.3 String 类型 1.4 内存与分配 变量与数据交互的方式(一):移动 变量与数据交互的方式(二):克隆 只在栈上的数据:拷贝…...
和JWT 详解)
跨域(CORS)和JWT 详解
跨域 (CORS) 概念 同源策略 (Same-Origin Policy) 同源策略是一项浏览器安全特性,它限制了一个网页中的脚本如何与另一个来源(域名、协议、端口)的资源进行交互。这对于防止跨站点请求伪造和数据泄露非常重要。 为什么需要跨域? 跨域问题通…...

前端框架Vue学习 ——(二)Vue常用指令
文章目录 常用指令 常用指令 指令: HTML 标签上带有 “v-” 前缀的特殊属性,不同指令具有不同含义。例如: v-if, v-for… 常用指令: v-bind:为 HTML 标签绑定属性值,如设置 href,css 样式等 <a v-bind:href"…...
`flash_erase` 擦除Flash存储器)
Linux 指令心法(十四)`flash_erase` 擦除Flash存储器
文章目录 flash_erase 作用flash_erase的主要特点和使用场景flash_erase命令应用方法flash_erase命令可以解决哪些问题?flash_erase命令使用时注意事项 flash_erase 作用 这是一个用于擦除Flash存储器的命令。它可以擦除指定的Flash块或扇区,以便在写入新数据之前…...
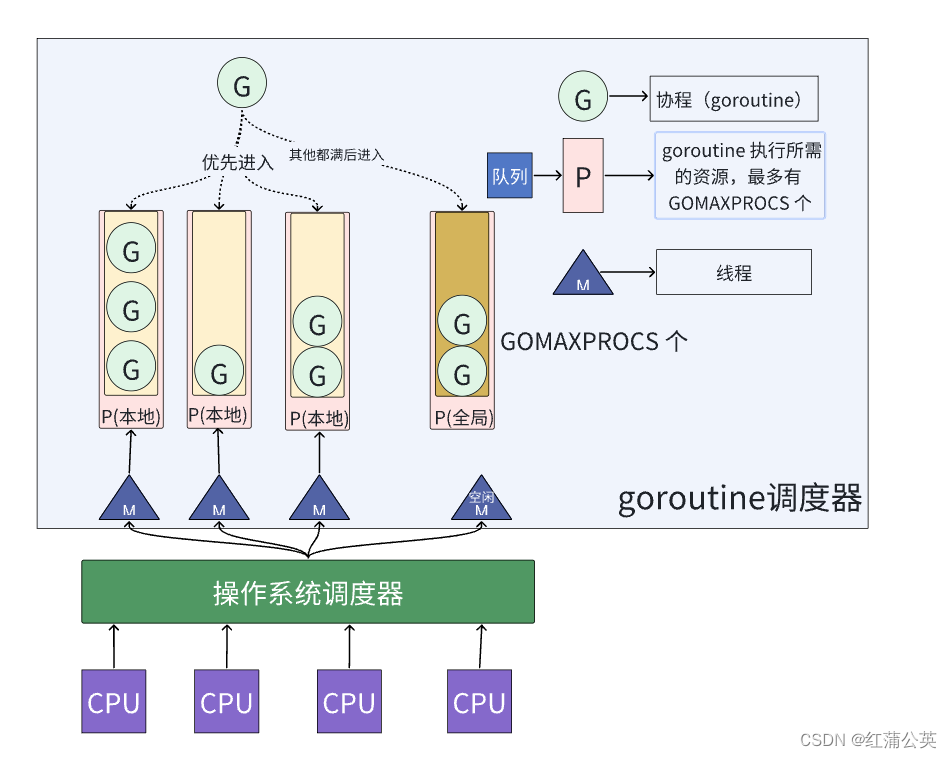
GoLong的学习之路(二十一)进阶,语法之并发(go最重要的特点)(协程的主要用法)
并发编程在当前软件领域是一个非常重要的概念,随着CPU等硬件的发展,我们无一例外的想让我们的程序运行的快一点、再快一点。Go语言在语言层面天生支持并发,充分利用现代CPU的多核优势,这也是Go语言能够大范围流行的一个很重要的原…...

加快网站收录 3小时百度收录新站方法
加快网站收录 3小时百度收录新站方法 3小时百度收录新站方法说起来大家可能不相信,但这确实是真实的(该方法是通过技术提交,让百度快速抓取收录您的网站,不管你网站有没有备案,都能在短时间内被收录,要是你的网站迟迟不…...

GPT实战系列-ChatGLM3本地部署CUDA11+1080Ti+显卡24G实战方案
目录 一、ChatGLM3 模型 二、资源需求 三、部署安装 配置环境 安装过程 低成本配置部署方案 四、启动 ChatGLM3 五、功能测试 新鲜出炉,国产 GPT 版本迭代更新啦~清华团队刚刚发布ChatGLM3,恰逢云栖大会前百川也发布Baichuan2-192K,一…...
图片怎么转换成pdf?
图片怎么转换成pdf?图片可以转换成PDF格式文档吗?当然是可以的呀,当图片转换成PDF文件类型时,我们就会发现图片更加方便的打开分享和传播,而且还可以更加安全的保证我们的图片所有性。我们知道PDF文档是可以加密的&…...
【源码】医学影像PACS实现三维影像后处理等功能
医学影像诊断技术近年来取得了快速发展,包括高性能的影像检查设备的临床应用和数字信息技术的图像显示、存储、传输、处理、识别,这些技术使得计算机辅助检测和诊断成为可能,同时人工智能影像诊断也进入了人们的视野。这些技术进步提高了疾病…...

DOCTYPE是什么,有何作用、 使用方式、渲染模式、严格模式和怪异模式的区别?
前言 持续学习总结输出中,今天分享的是DOCTYPE是什么,有何作用、 使用方式、渲染模式、严格模式和怪异模式的区别。 DOCTYPE是什么,有何作用? DOCTYPE是HTML5的文档声明,通过它可以告诉浏览器,使用那个H…...

Go语言实现HTTP正向代理
文章目录 前言实现思路代码实现 前言 正向代理(Forward Proxy)是一种代理服务器的部署方式,它位于客户端和目标服务器之间,代表客户端向目标服务器发送请求。正向代理可以用来隐藏客户端的真实身份,以及在不同网络环境…...
第11章_数据处理之增删改
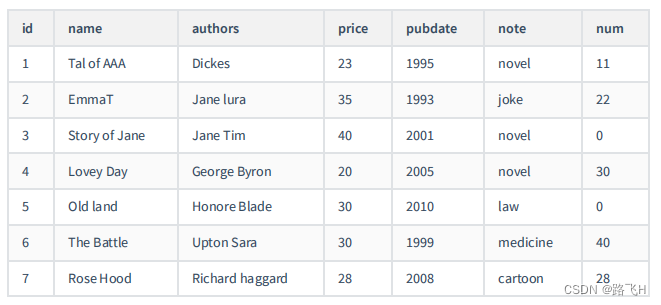
文章目录 1 插入数据1.1 实际问题1.2 方式 1:VALUES的方式添加1.3 方式2:将查询结果插入到表中演示代码 2 更新数据演示代码 3 删除数据演示代码 4 MySQL8新特性:计算列演示代码 5 综合案例课后练习 1 插入数据 1.1 实际问题 解决方式&#…...

数据时代的新引擎:数据治理与开发,揭秘数据领域的黄金机遇!
文章目录 一、数据时代的需求二、数据治理与开发三、案例分析四、黄金机遇《数据要素安全流通》《Python数据挖掘:入门、进阶与实用案例分析》《数据保护:工作负载的可恢复性 》《Data Mesh权威指南》《分布式统一大数据虚拟文件系统 Alluxio原理、技术与…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
