AVL树性质和实现
AVL树
AVL是两名俄罗斯数学家的名字,以此纪念
与二叉搜索树的区别
AVL树在二叉搜索树的基础上增加了新的限制:需要时刻保证每个树中每个结点的左右子树高度之差的绝对值不超过1
因此,当向树中插入新结点后,即可降低树的高度,从而减少平均搜索长度
平衡因子
为了能方便处理平衡二叉搜索树的限制条件,通常会引入平衡因子的概念
某一节点的平衡因子=其右子树高度-其左子树高度
在AVL树中,并不是一定需要平衡因子的,有些代码的AVL树就没有平衡因子。
这里引入平衡因子只是更方便的去判断树是否平衡了
AVL树的效率推算
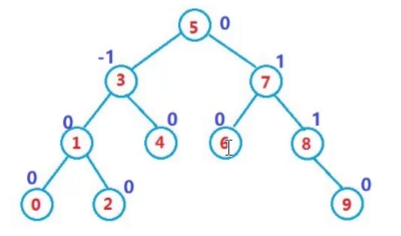
我们知道树的增删查改的效率是与树的高度有关的
假如AVL树是满二叉树,此时:2h-1=N
假如AVL树不是满二叉树,设最底层的节点个数为X,此时:2h-X=N。X的范围为[1,最后一层结点树-1]
此时上述两种情况都可以得出树的高度的数量级为logN,因此增删查改的时间复杂度为O(logN)
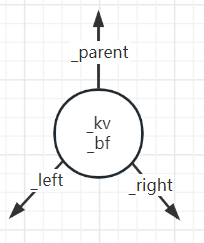
AVL树的节点设计
首先,与二叉搜索树相比,每个节点多了一个平衡因子(balance factor)
其次,为了满足一定需求,还多了个_parent指针,指向节点的父亲
template<class K,class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K,V>* _left;AVLTreeNode<K,V>* _right;AVLTreeNode<K,V>* _parent;int _bf;//平衡因子AVLTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
这是三叉链
AVL树的框架设计
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://……
private:Node* _root=nullptr;
};
AVL树的插入
在面试时几乎不会让你手撕AVL树的插入。重要的是了解思想。
但让你手撕一个旋转是有可能的
插入的逻辑
AVL树是在二叉搜索树的基础上引入了平衡因子,因此AVL树的插入分为两个步骤:
- 按照二叉搜索树的方式插入新节点(多了个链接
_parent) - 插入后,更新节点的平衡因子
首先注意:新插入的节点只会对其父亲和其祖先的平衡因子造成影响
插入节点的_parent的平衡因子是一定需要调整的;在插入之前其_parent的平衡因子有三个可能值1、-1、0,插入节点后:
- 如果插入到
_parent的左侧,则_parent的平衡因子–即可 - 如果插入到
_parent的右侧,则_parent的平衡因子++即可
此时:_parent的平衡因子可能有三大种情况:
- 如果
_parent的平衡因子为0,说明插入之前的平衡因子为正负1,插入后被调整成0,满足AVL树的性质,插入成功,插入结束 - 如果
_parent的平衡因子为±1,说明插入之前的平衡因子为0,此时树的高度增加,那么就需要继续向上更新祖先的平衡因子,直至某一祖先的平衡因子为0或者更新到根节点,才算插入成功,停止更新,插入结束。 - 如果
_parent的平衡因子为±2,此时违反了AVL树的性质,需要进行旋转处理。处理完成则算插入成功,插入结束
更新平衡因子
最坏的情况是一直更新到根,如下图: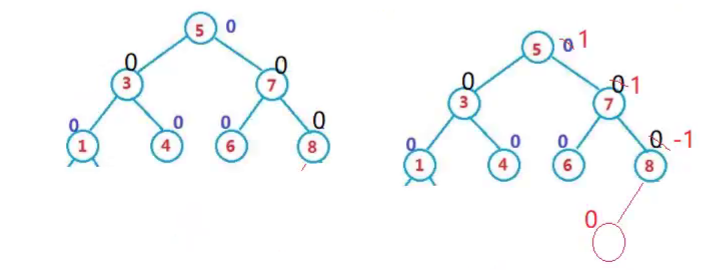
因此在更新平衡因子时,我们的循环条件为:while(parent)
因为只有根节点的
_parent为空。所以当更新完根节点的平衡因子后,循环结束
while (parent)
{if (cur == parent->_left)//节点插入在父亲左边{parent->_bf--;}else if (cur == parent->_right)//节点插入在父亲右边{parent->_bf++;}//进一步判断祖先节点的平衡因子if (parent->_bf == 0)//父亲的平衡因子为0,循环结束{break;}else if (parent->_bf == 1 || parent->_bf == -1)//父亲的平衡因子为1或-1,则需要继续向上调整{cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//父亲的平衡因子为2或-2,则需要旋转,且选择完后树一定平衡,故结束循环{//左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//右左双旋if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}//左右双旋if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else//其他情况,此时说明在插入之前树就已经不是平衡树了{assert(false);}
}
最后一个
else中的assert(false)看似是无用的,因为parent不可能是绝对值大于2的。但是代码都是人写的,不可排除一开始的树就是有问题的。因此这句代码很重要
AVL树的旋转
根据节点插入位置的不同,AVL树的旋转分为四种:
- 新节点插入较高左子树的左侧–左左:右单旋
- 新节点插入较高右子树的右侧–右右:左单旋
- 新节点插入较高左子树的右侧—左右:先左单旋再右单旋(左右双旋)
- 新节点插入较高右子树的左侧—右左:先右单旋再左单旋(右左双旋)
何时使用何种旋转:
假如以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑:
-
pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR
-
当pSubR的平衡因子为1时,执行左单旋
-
当pSubR的平衡因子为-1时,执行右左双旋
-
-
pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL
-
当pSubL的平衡因子为-1是,执行右单旋
-
当pSubL的平衡因子为1时,执行左右双旋
-
旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新
右单旋
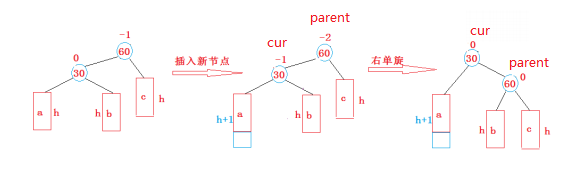
上图在插入前,AVL树是平衡的。新节点插入到30的左子树(注意:此处不是左孩子)中,30左子树增加了一层,导致以60为根的二叉树不平衡,要让60平衡,只能将60左子树的高度减少一层,右子树增加一层,即将左子树往上提,这样60转下来,因为60比30大,只能将其放在30的右子树,而如果30有右子树,右子树根的值一定大于30,小于60,只能将其放在60的左子树,旋转完成后,更新节点的平衡因子即可
在旋转过程中,有以下几种情况需要考虑:
-
cur节点的右孩子可能存在,也可能不存在
-
parent可能是根节点,也可能是子树
如果是根节点,旋转完成后,要更新根节点
如果是子树,可能是某个节点的左子树,也可能是右子树
这两点是所有旋转情况都需要考虑的
右单旋的核心操作:把cur的右孩子给到parent的左,再把parent给到cur的右
代码:
void RotateR(Node* parent)//parent的平衡因子绝对值为2
{Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;//把cur的右孩子给到parent的左if (curright)//如果cur的右孩子存在,则更新其父亲为parent{curright->_parent = parent;}cur->_right = parent;//再把parent给到cur的右Node* ppnode = parent->_parent;//记录parent的原父亲节点,用于对cur的父亲进行更新parent->_parent = cur;//更新parent的父亲//对cur的父亲进行更新if (parent == _root)//parent即为根节点{_root = cur;cur->_parent = nullptr;//那么cur作为新的根,其父亲为空}else//parent是子树{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;//更新完后,平衡因子一定为0
}
左单旋
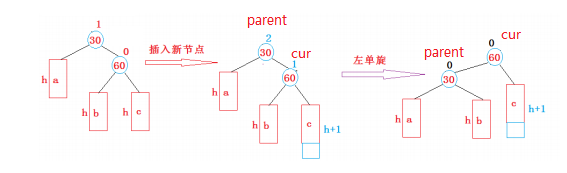
左单旋的核心操作与右单旋的核心操作正好是镜像的
左单旋的核心操作:把cur的左给parent的右,再把parent给到cur的左
代码:
void RotateL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;//把cur的左给parent的右if (curleft)//如果cur的左存在,则更新其父亲{curleft->_parent = parent;} cur->_left = parent;//再把parent给到cur的左Node* ppnode = parent->_parent;//记录parent的原父亲节点,用于对cur的父亲进行更新parent->_parent = cur;//对cur的父亲进行更新if (parent == _root){_root = cur;cur->_parent = nullptr;}else//说明左旋的部分只是某棵树的局部{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}
右左双旋
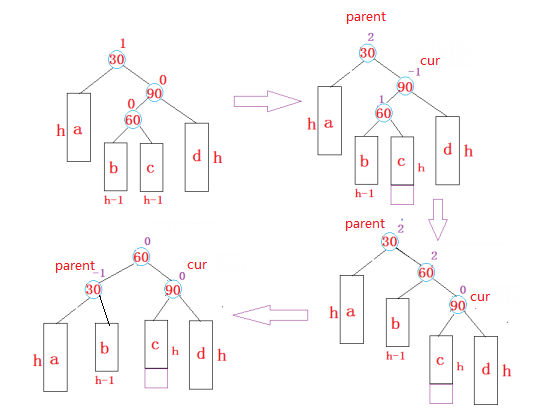
先对90进行右单旋,再对30进行左单旋
两次旋转。第一次旋转使其变成单纯的右边高,第二次旋转对应的左单旋
双旋代码难的不是旋转,而是平衡因子的更新
从图中可以看到:最终60成了根,60的左孩子给了parent的右边,60的右孩子给了cur的左边
因此平衡因子的更新分为两种情况:
- h == 0:那么60则作为新插入的节点,此时60的bf == 0,那么parent和cur的bf也一定为0
- h>=0:
- 假如新结点插入在60的左边,即60的bf == -1。那么最终parent的bf == 0,cur的bf == 1
- 假如新结点插入在60的右边,即60的bf == 1。那么最终parent的bf == -1,cur的bf == 0
- 而60作为根节点最终bf一定为0
代码:
void RotateRL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;//先右旋再左旋RotateR(cur);RotateL(parent);//更新平衡因子if (bf == 0){parent->_bf = 0;cur->_bf = 0;curleft->_bf = 0;}else if (bf == 1){parent->_bf = -1;cur->_bf = 0;curleft->_bf = 0;}else if (bf == -1){parent->_bf = 0;cur->_bf = 1;curleft->_bf = 0;}else{assert(false);}
}
左右双旋
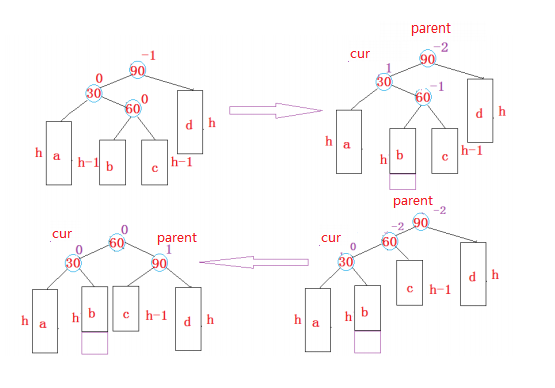
与右左双旋是镜像的,不再赘述
代码:
void RotateLR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;//先左旋再右旋RotateL(cur);RotateR(parent);//更新平衡因子if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else{assert(false);}
}
AVL树插入的完整代码
bool Insert(const pair<K, V>& kv)
{//先帮助插入节点找到正确位置if (_root == nullptr)//树为空{_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){//插入节点大于根节点if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first)//插入节点小于根节点{parent = cur;cur = cur->_left;}else//所插入节点已经存在{return false;}}cur = new Node(kv);if (cur->_kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//控制平衡因子while (parent)//{if (cur == parent->_left)//节点插入在父亲左边{parent->_bf--;}else if (cur == parent->_right)//节点插入在父亲右边{parent->_bf++;}//进一步判断祖先节点的平衡因子if (parent->_bf == 0)//父亲的平衡因子为0,循环结束{break;}else if (parent->_bf == 1 || parent->_bf == -1)//父亲的平衡因子为1或-1,则需要继续向上调整{cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//父亲的平衡因子为2或-2,则需要旋转,且选择完后树一定平衡,故结束循环{//左单旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}//右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//右左双旋if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}//左右双旋if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else//其他情况,此时说明在插入之前树就已经不是平衡树了{assert(false);}}}//左单旋
void RotateL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;} cur->_left = parent;Node* ppnode = parent->_parent;//记录parent的原父亲节点parent->_parent = cur;//对cur的父亲进行更新if (parent == _root){_root = cur;cur->_parent = nullptr;}else//说明左旋的部分只是某棵树的局部{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}//右单旋
void RotateR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;//让右节点接到parent的左边,再将parent接到cur的右边parent->_left = curright;if (curright){curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;//记录parent的原父亲节点parent->_parent = cur;//对cur的父亲进行更新if (parent == _root){_root = cur;cur->_parent = nullptr;}else//说明右旋的部分只是某棵树的局部{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}//右左双旋
void RotateRL(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;//先右旋再左旋RotateR(cur);RotateL(parent);//更新平衡因子if (bf == 0){parent->_bf = 0;cur->_bf = 0;curleft->_bf = 0;}else if (bf == 1){parent->_bf = -1;cur->_bf = 0;curleft->_bf = 0;}else if (bf == -1){parent->_bf = 0;cur->_bf = 1;curleft->_bf = 0;}else{assert(false);}
}//左右双旋
void RotateLR(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;//先左旋再右旋RotateL(cur);RotateR(parent);//更新平衡因子if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 1;cur->_bf = -1;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else{assert(false);}
}
AVL树的验证
验证AVL树分为两步:
-
验证其为二叉搜索树:如果中序遍历历可得到一个有序的序列,就说明为二叉搜索树(这里就不详细介绍了,详情可以看二叉搜索树那里)
-
验证其为平衡树:
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
int TreeHeight(Node* root) {if (root == nullptr)return 0;int leftHeight = TreeHeight(root->_left);int rightHeight = TreeHeight(root->_right);return rightHeight > leftHeight ? rightHeight + 1: leftHeight + 1; }bool IsBalance()//两个IsBalance构成重载 {return IsBalance(_root); }bool IsBalance(Node* root) {if (root == nullptr)return true;int leftHeight = TreeHeight(root->_left);int rightHeight = TreeHeight(root->_right);if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right); }这里给出一个调试技巧:
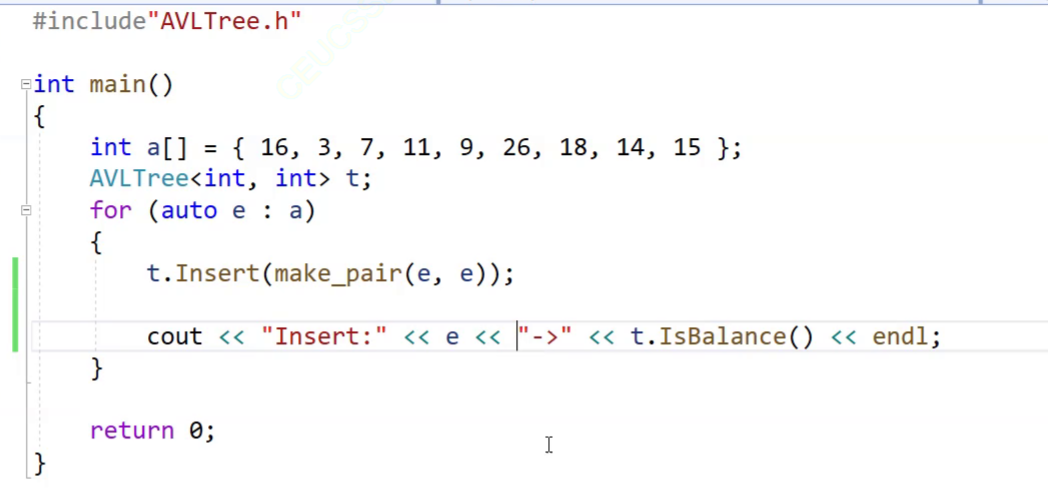 假如我运行出现了下面的情况
假如我运行出现了下面的情况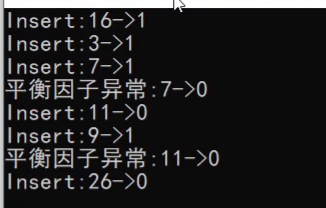
我们现在知道在插入11的时候出了问题,那么就可以针对e=11时进行调试
但如果现在有100个值,我在第99个值才出现问题,那是不是需要按F10按99次呢?
两种方法,:
-
一个是利用条件断点
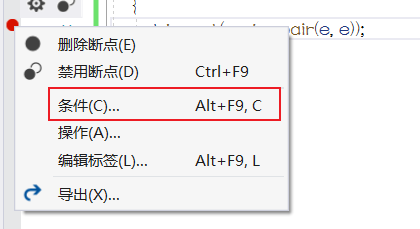
-
还一个是我们自己写代码让它停到想停的地方
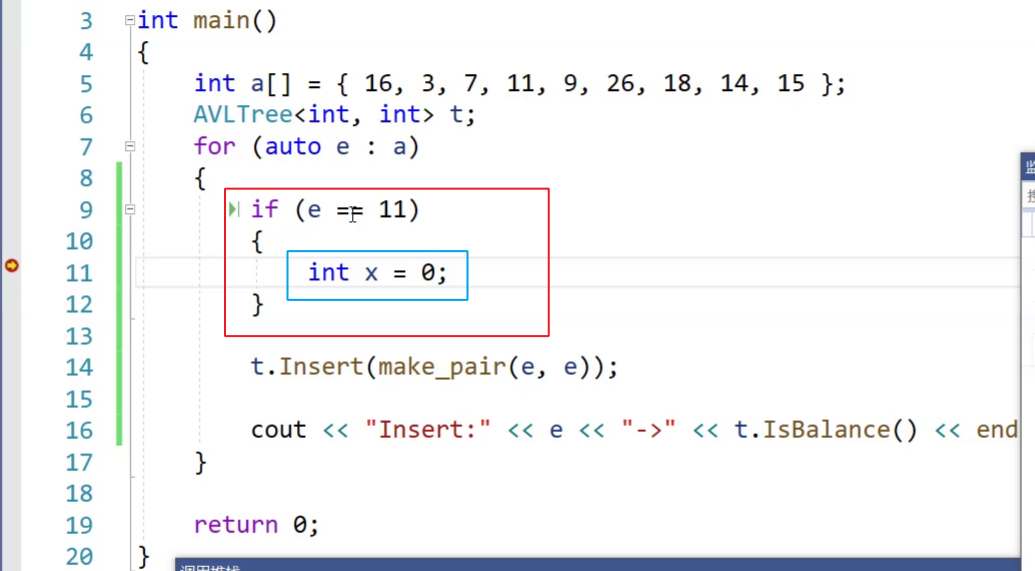
这里的
int x=0;是随便写的,目的是能让断点在这里停下来。因为断点打在空行上是停不住的当然,我停在断点处不是为了调
int x=0;,而是为了调下面
AVL树的删除
了解即可

总结
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 l o g 2 ( N ) log_2 (N) log2(N)。
但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

AVL树性质和实现
AVL树 AVL是两名俄罗斯数学家的名字,以此纪念 与二叉搜索树的区别 AVL树在二叉搜索树的基础上增加了新的限制:需要时刻保证每个树中每个结点的左右子树高度之差的绝对值不超过1 因此,当向树中插入新结点后,即可降低树的高度&…...

出口贸易媒体发稿推广6个技巧提升品牌知名度-华媒舍
1. 出口贸易媒体介绍 出口贸易媒体是指专注于报道国际贸易、跨境业务和进出口市场的媒体平台。这些媒体对于企业发展来说至关重要,可以帮助品牌扩大影响力、提升知名度,促进商业合作。下面介绍6个出口贸易媒体发稿推广技巧,帮助企业更好地利…...
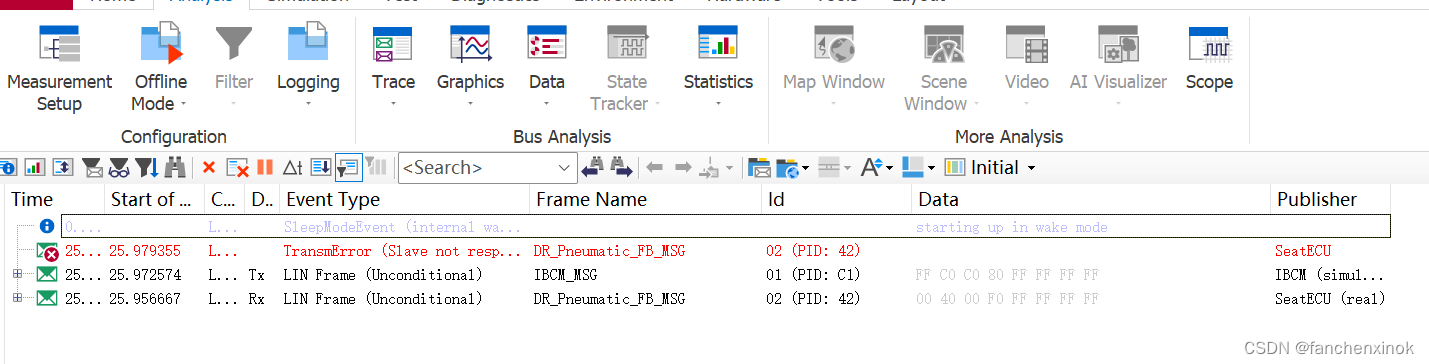
学习笔记:CANOE模拟LIN主节点和实际从节点进行通信测试
先写点感想,在LIN开发阶段,我一般用图莫斯USB工具来进行模拟主机节点发送数据。后来公司买了CANOE工具就边学习边搭建了LIN的测试工程,网上的资料真的很少,主要是靠自己一点点摸索前进,总算入门。几个月后的今天&#…...
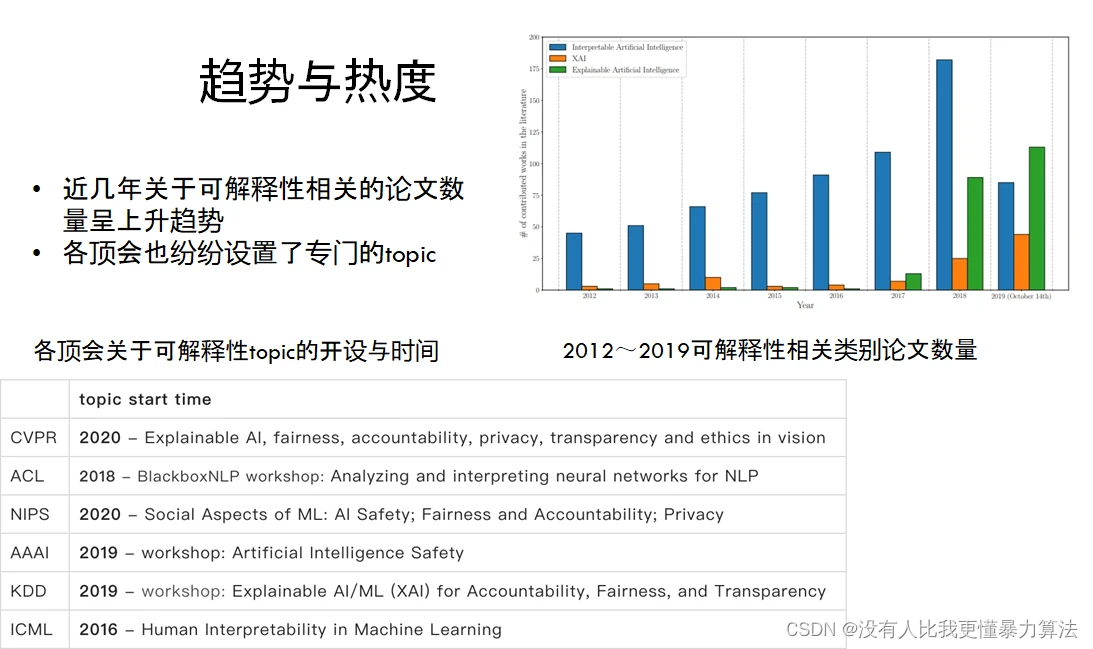
模型可解释性
模型可解释性 前言导读Background1、为什么需要可解释性?2、诞生背景3、研究现状4、常见的模型可解释性方法4.1 基于模型自身的可解释性1)Explanation Generation2)Prototype Network 4.2 基于结果的可解释性 5、应用前景6、面临挑战 前言导读…...

Django初窥门径-自定义用户模型
前言 自定义用户模型在Django应用中是一个重要的话题,它涉及到如何根据您的项目需求以及特定的用户身份验证和授权需求来调整用户模型。在以下前言中,我将讲述为什么自定义用户模型是如此重要以及其潜在的优势: 随着Web应用的不断发展&…...
微信小程序文件上传wx.uploadFile
网页版查看了一下负载要求是这样 wx.uploadFile({url: ${wx.getStorageSync(apiUrl)}//sysFileInfo/upload?token${wx.getStorageSync(token)}, // 仅为示例,非真实的接口地址filePath: files[0].url,name: file,formData: {secretFlag: Y },success: (res) > {…...
支持内录系统声音的Mac录屏软件Omi Recorder
Screen Recorder by Omi是一款功能强大的屏幕录制应用程序。它可用于在Windows和Mac计算机上捕获屏幕,以便进行演示、教程、游戏录制、视频编辑等各种用途。 以下是该应用程序的一些主要特点: 支持高清录制:Omi Screen Recorder可以以高达6…...
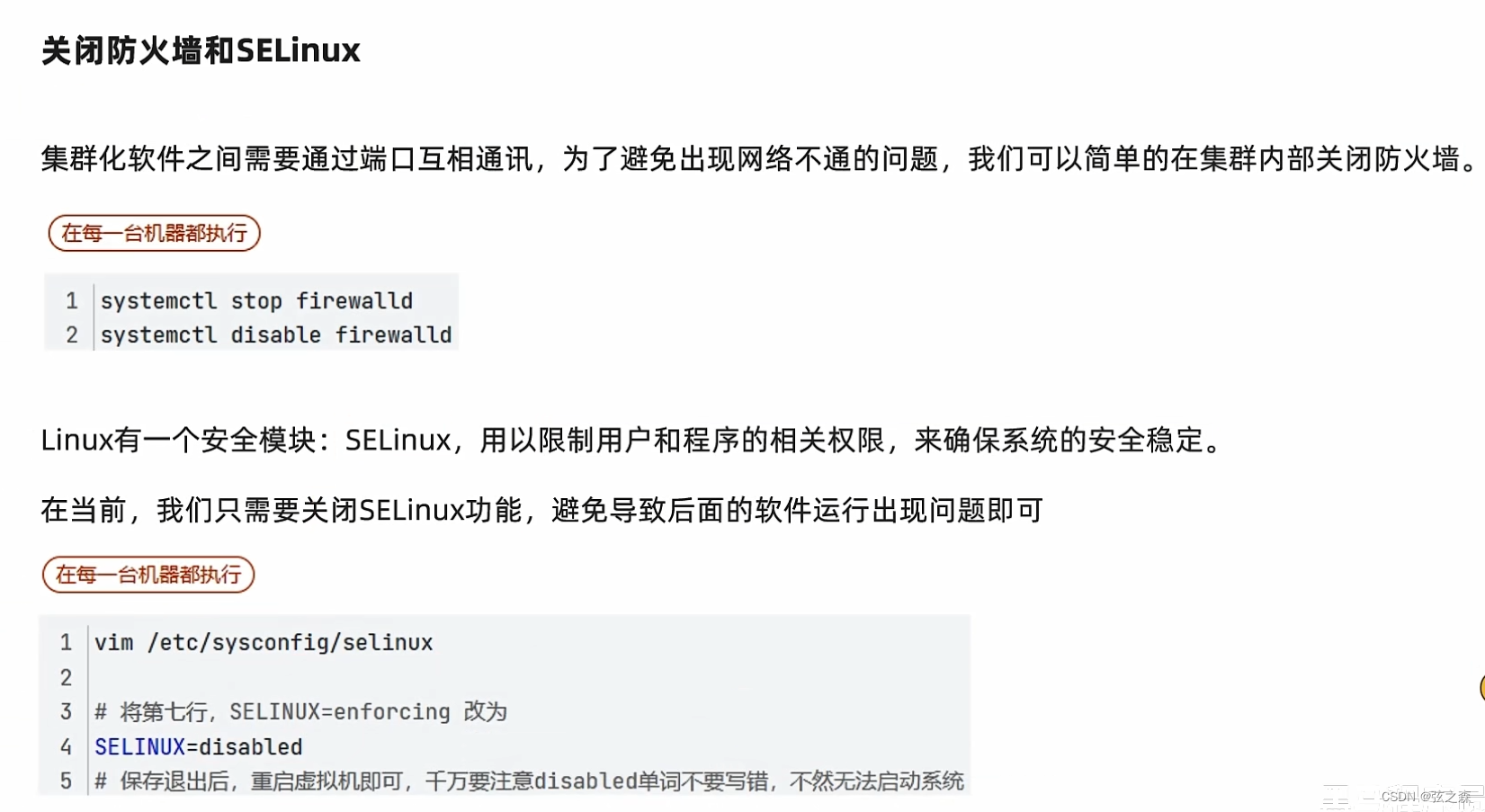
一、Hadoop初始化配置(final+ubuntu保姆级教程)
1、配置虚拟机 三台虚拟机,分别为node1、node2、node3,内存分别为4G、2G、2G,现存最好为(>40G),如下: 2、修改主机名 分别打开三台虚拟机,root用户输入一下命令: no…...

Linux常用的包管理工具
Linux系统中有两个常用的包管理工具,分别是yum和apt。 1. yum命令 yum是Red Hat公司开发的一种包管理器,主要用于安装、更新、卸载和管理RPM包。它是基于RPM包管理系统的,可以自动解决软件包依赖关系问题。 常用yum命令: - 安…...
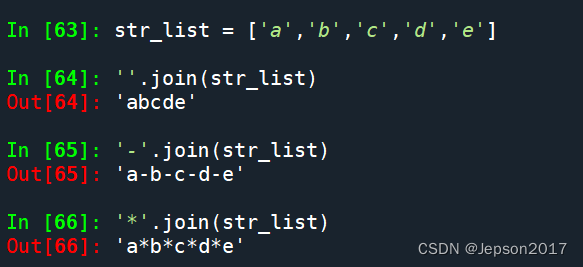
python随机生成指定长度的字符串
需求:随机生成一个指定长度的字符串(数字和小写字母) 涉及到的python知识点 (1)python模块包:random random.choice(sequence):从指定的序列中获取一个随机元素 random.choice(sequence)从序…...

语音识别接口试用
语音识别结果对比 1.jonatasgrosman/wav2vec2-large-xlsr-53-chinese-zh-cn 啊五包你没有什么问题嗓局问的这老受刚来指伯间我想就了解其二联地完觉全没问题犹该奖姐家女标要等到老师主动据奖定练择因位我主要奖的是耶号联接最长加展们如果说宁士比到六点级到一到另年级的家长…...

Java的数组使用
数组的定义: package The_First_Stage.The_beginner_level_Java_SE.Arrawy;/*** 数组的作用:用来存储相同类型的数据* 以int类型数据为案例:数组用来存储int类型数据* 1》声明定义数组* int【】 arr 定义一个int类型的数组,名字…...

基于STC15单片机温度光照蓝牙传输-proteus仿真-源程序
一、系统方案 本设计采用STC15单片机作为主控器,液晶1602显示,DS18B20采集温度,光敏电阻采集光照、按键设置温度上下限,测量温度小于下限,启动加热,测量温度大于上限,启动降温。 二、硬件设计 …...

Jmter接口网站压力测试工具
首先下载Jmeter 官方地址:Apache JMeter - Apache JMeter™ 安装Jmeter 把下载的文件进行解压,产生如下目录: 打开bin文件夹下的jmeter.bat文件及进入程序的主界面窗体jmeter.log是日志文件。 主意:需要配置java环境。 jmter创…...

7.2 创建和销毁条件变量
方法 pthread_cond_init(condition, attr) pthread_cond_destroy(condition) pthread_condattr_init(attr) pthread_condattr_destroy(attr) 用法 条件变量的类型为pthread_cond_t,必须在使用之前初始化。有如下两种方法来初始化条件变量: 声明时初…...

九凌网络:谷歌seo优化和外贸建站的五大优势
九凌网络是专注于谷歌SEO和外贸网站建设技术研发的技术型公司。九凌网络为外贸企业提供优质的外贸建站和谷歌优化服务,目前全国合作过的外贸企业超过8000家,覆盖全国12个省,超过60个地级市,在运营的谷歌seo优化客户300多家&#x…...
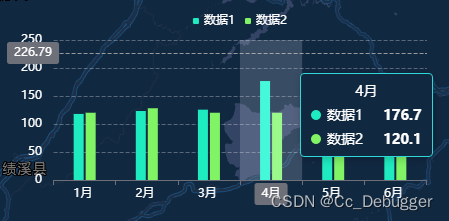
【vue3/echarts】vue3中使用echarts/饼图/双轴双数据柱状图
npm下载echarts 引入使用 <script> import Box from "/components/box.vue"; import { onMounted } from vue; import { init } from echarts; export default {components: {Box: Box},setup() {onMounted(() > {// 饼图const charEle document.getElem…...

【左程云算法全讲4】比较器和堆
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于左程云算法课程进行的,每个知识点的修正和深入主要参考…...
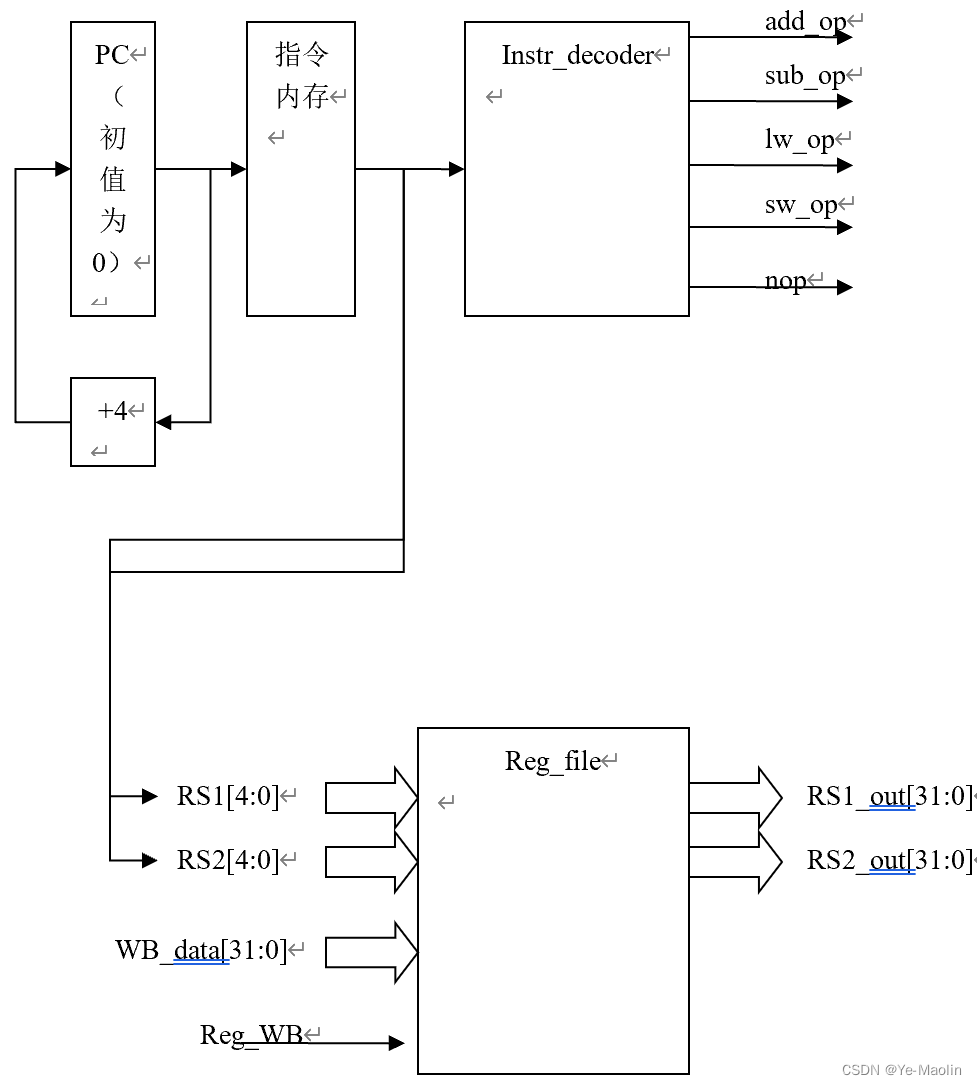
【计算机组成与设计】Chisel取指和指令译码设计
本次试验分为三个部分: 目录 设计译码电路 设计寄存器文件 实现一个32个字的指令存储器 设计译码电路 输入位32bit的一个机器字,按照课本MIPS 指令格式,完成add、sub、lw、sw指令译码,其他指令一律译码成nop指令。输入信号名…...
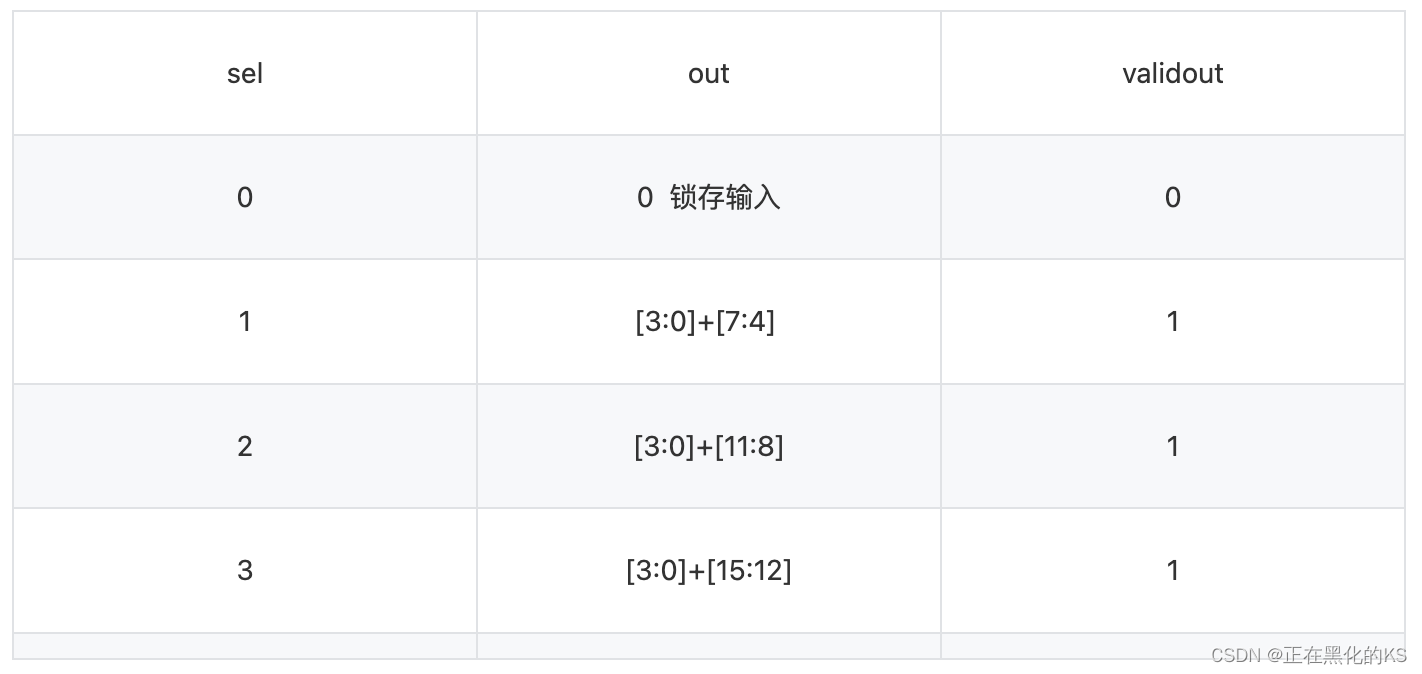
「Verilog学习笔记」位拆分与运算
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 1、寄存器的位是可以分开单独运算的,并不是一个输入就一定是一个数据,在很多情况下,一个输入既包括数据又包括地址等其他有效信息 2、需…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...