【学习笔记】NOIP爆零赛7
结论专场,结果被踩暴了
青鱼和序列
赛时的做法是,维护∑ai×i\sum a_i\times i∑ai×i的取值,发现只和最后一次操作222的位置有关,于是递推O(n)O(n)O(n)解决。
赛后发现还有更神奇的结论 第二个结论是,第一次进行操作222过后,aaa序列变成回文的了,所以这之后1,21,21,2操作就是等价的了。
这两个结论单独来看都很容易发现。不过接下来这个结论可能不容易看出:只要进行了操作222,那么最后的结果就是一定的。事实上这不难从前222个结论中看出。不过如果打表还是很容易看出的
看来我猜结论的功底还是太菜了,还是要多尝试啊
青鱼和怪兽
猜了一个结论,直接二分答案就可以解决。
同样不难通过打表证明这个结论是正确的
青鱼和区间
垃圾题解写的像shit一样,真就谜语人呗
这个结论太小,以至于我看不见
这道题的思维量还是非常高的,不过nknknk这波玄学过题确实佩服。。。
我是joker,以为这道题转移比较难想,最后发现我连计数的对象都没搞清楚
如果不先入为主而是尝试推一下结论的话这道题还是可以分析的吧,但是最后那一步凭考场上的我是无论如何也推不出来的
首先最直白的翻译是,设SiS_iSi表示覆盖iii位置的区间的集合,那么合法的条件等价于SiS_iSi互不相同。
然后有一个结论:不存在i1<i2<j1<j2i_1<i_2<j_1<j_2i1<i2<j1<j2,使得Si1=Sj1≠Si2=Sj2S_{i_1}=S_{j_1}\ne S_{i_2}=S_{j_2}Si1=Sj1=Si2=Sj2
这个结论的正确性其实挺显然的,但是当时我没往这方面想,而是直接去刚dpdpdp了,现在想来确实是不明智的行为
那么我们把相同等价类的位置提出来,记作区间[li:ri][l_i:r_i][li:ri],那么这些区间要么包含要么不相交,这个结构就非常显而易见了:我们可以把原序列划分成若干个连续段,同时不存在两个不属于同一个连续段的i,ji,ji,j使得Si=SjS_i=S_jSi=Sj。这个性质也等价于什么呢,对于询问区间[i:j][i:j][i:j],要么i,ji,ji,j在同一段中,要么[i:j][i:j][i:j]不能制造断点,也就是说[i:j][i:j][i:j]恰好是若干完整的段拼起来的。
现在我们只差最后一步:如何对这些若干不相交的[li:ri][l_i:r_i][li:ri]计数?
我竟就倒在了这里。。。
考虑一个普通至极的思路:正难则反。也就是说,我们减去分出来的段数<n<n<n的方案数。那么我们考虑,假设分成了jjj段,根据前面的观察,我们要把这分出来的jjj段区分出来,然后对于长度为lll的一段,我们需要注意端点是不能包括在区间中的,因此有(l−2)(l−1)2\frac{(l-2)(l-1)}{2}2(l−2)(l−1)个可选择的区间,方案数为2(l−2)(l−1)22^{\frac{(l-2)(l-1)}{2}}22(l−2)(l−1)。
有了上述动机,我们设dpidp_idpi表示长度为iii的答案,有转移式:dpi=2i(i+1)2−∑j<idpjfi,jdp_i=2^{\frac{i(i+1)}{2}}-\sum_{j<i}dp_jf_{i,j}dpi=22i(i+1)−∑j<idpjfi,j,其中fi,jf_{i,j}fi,j表示把iii分成jjj段的所有方案的系数和。
复杂度O(n3)O(n^3)O(n3)。可以用多项式工业优化到O(npoly(n))O(n\text{poly}(n))O(npoly(n)),但是有点复杂并且我不太懂所以就咕了
这就是天才和凡人的差距吗
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define ll long long
#define pb push_back
#define fi first
#define se second
using namespace std;
const int N=305;
int n,mod;
ll pw[N*N],dp[N][N],res[N];
void add(ll &x,ll y){x=(x+y)%mod;
}
int main(){cin>>n>>mod;pw[0]=1;for(int i=1;i<=n*n;i++)pw[i]=pw[i-1]*2%mod;dp[0][0]=1;for(int i=0;i<n;i++){for(int j=0;j<=i;j++){if(dp[i][j]){for(int k=1;k<=n-i;k++){add(dp[i+k][j+1],dp[i][j]*pw[(k-1)*(k-2)/2]);}}}}for(int i=1;i<=n;i++){res[i]=pw[i*(i+1)/2];for(int j=1;j<i;j++){res[i]=(res[i]-res[j]*dp[i][j])%mod;}}cout<<(res[n]+mod)%mod;
}
青鱼和游戏
考场上爆蛋了
这题爆蛋有两个原因:一是确实不会做,二是t3t3t3确实被卡住了
说白了就是太菜了
相关文章:

【学习笔记】NOIP爆零赛7
结论专场,结果被踩暴了 青鱼和序列 赛时的做法是,维护∑aii\sum a_i\times i∑aii的取值,发现只和最后一次操作222的位置有关,于是递推O(n)O(n)O(n)解决。 赛后发现还有更神奇的结论 第二个结论是,第一次进行操作…...

一文读懂账号体系产品设计
一、账号体系的概念及价值账号体系是用户在各平台上的通行证。平台给与用户可持续的服务,用户在平台上获取价值,中间的媒介,便是账号体系。阿境将其理解为维系用户与平台之间的枢纽。注:本文中,账号账户,二…...
从“入门”到“专家”,一份3000字完整的性能测试体系的知识分享
随着科技的飞速发展,软件产品广泛应用于各个行业领域,人们对计算机和网络的依赖性越来越大,对新奇事物也越来越感兴趣,成千上万的用户活跃在庞大的网络系统中,这给提供服务的系统带来严重的负荷,"高并…...

构建对话机器人:Rasa3安装和基础入门
在开源对话机器人中,Rasa社区很活跃,在国内很多企业也在使用Rasa做对话机器人,有rasa开发经验的往往是加分项。 当年实习的时候接触到了Rasa,现在工作中也使用Rasa,因此,写写一些经验文档,有助后…...
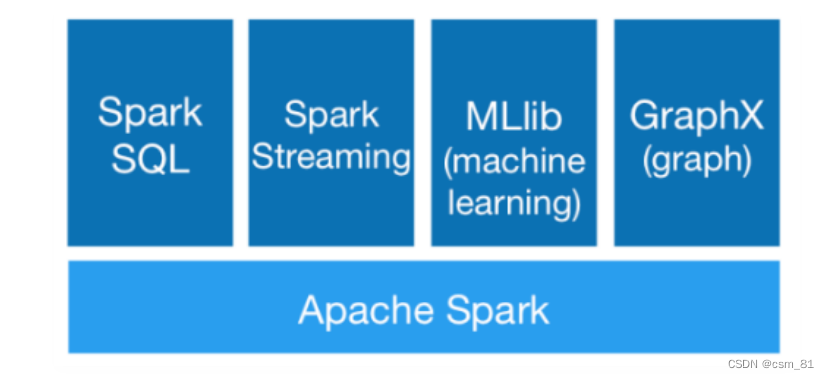
Spark计算框架入门笔记
Spark是一个用于大规模数据处理的统一计算引擎 注意:Spark不仅仅可以做类似于MapReduce的离线数据计算,还可以做实时数据计算,并且它还可以实现类似于Hive的SQL计算,等等,所以说它是一个统一的计算引擎 既然说到了Spar…...

入职数据分析公认的好书|建议收藏
众所周知,数据分析经常出现在我们的日常生活中,各行各业都需要数据分析。可你知道什么是数据分析?它在企业里到底扮演什么角色?以及如果我们自己也想拥有数据分析的能力,以便更好的满足数据分析的需求,我们…...

Linux查找文件和目录,重定向输出 ,系统默认运行级别的查看和设置理论和练习
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

Redis源码---键值对中字符串的实现,用char*还是结构体
目录 前言 为什么 Redis 不用 char*? char* 的结构设计 操作函数复杂度 SDS 的设计思想 SDS 结构设计 SDS 操作效率 紧凑型字符串结构的编程技巧 小结 前言 对于 Redis 来说,键值对中的键是字符串,值有时也是字符串在 Redis 中写入一…...

算法 - 剑指Offer 表示数值的字符串
题目 请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。 数值(按顺序)可以分成以下几个部分: 若干空格 一个 小数 或者 整数 (可选)一个 ‘e’ 或 ‘E’ ,后面跟着一个 …...
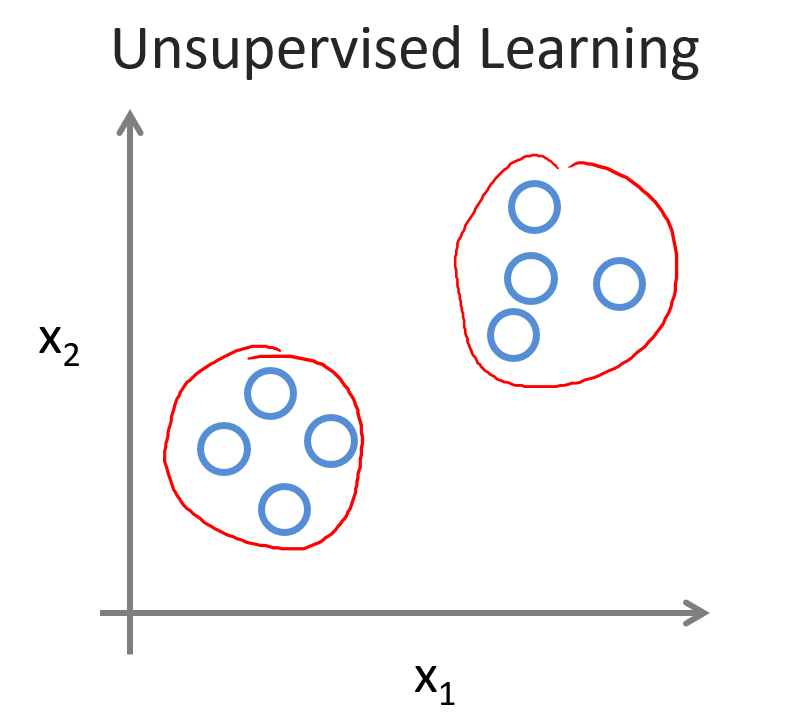
初识机器学习
监督学习与无监督学习supervised learning:监督学习,给出的训练集中有输入也有输出(标签)(也可以说既有特征又有目标),在此基础上让计算机进行学习。学习后通过测试集测试给相应的事物打上标签。…...
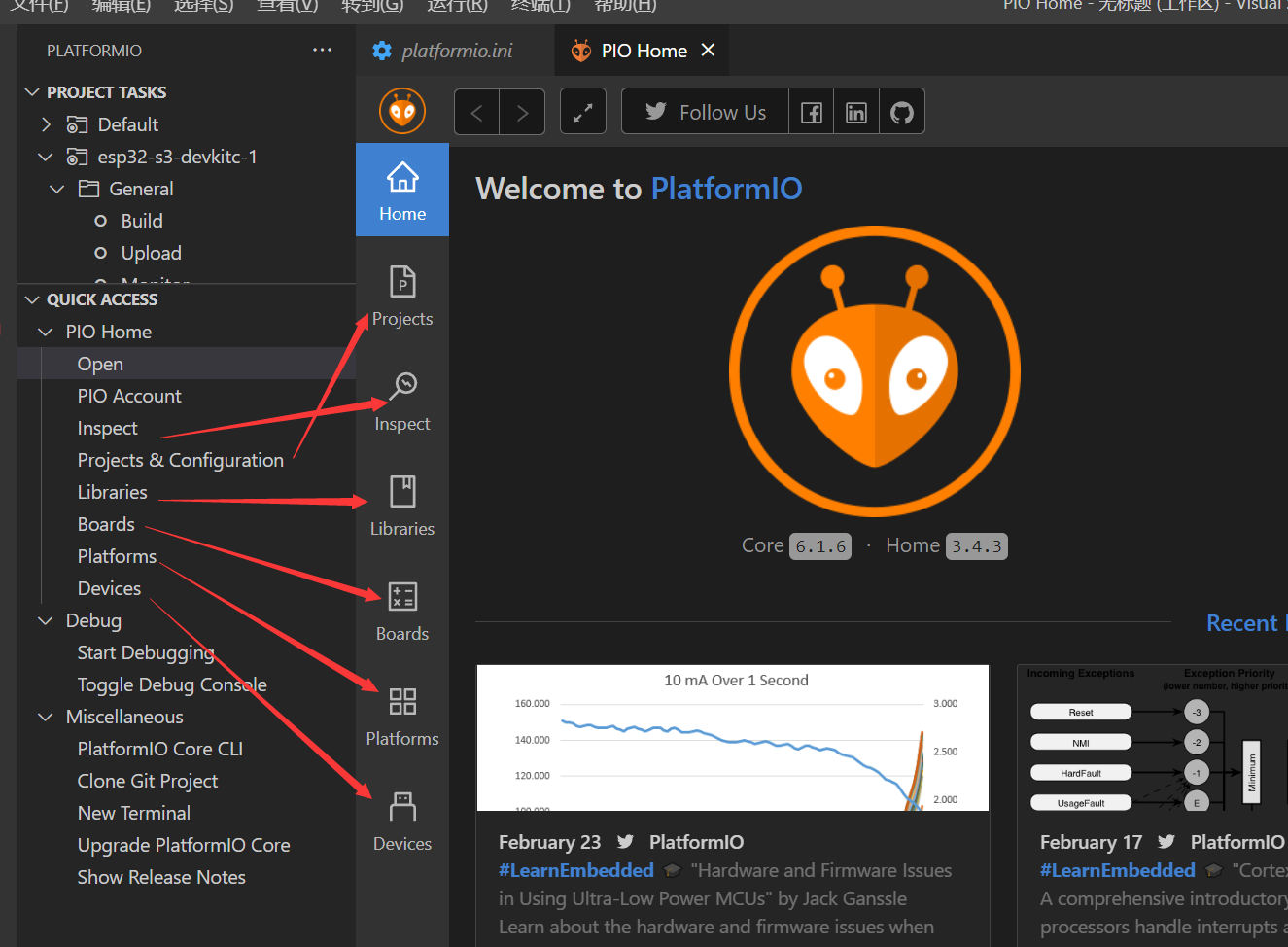
VsCode安装PlatformIO 开发ESP arduino,买的板子或者随便ESP,PlatformIO添加Board(不是自定义Board)
这次主要记录怎么给新建选板子的时候没有的板子下程序 我这里是一块 WiFi Kit 32 (V3) PlatformIO里面只有到V2 先从头开始,安装PlatformIO 安装PlatformIO 直接搜索安装 安装有时候会比较慢,左侧出现蚂蚁图标之后点击会显示 右下角会提示正在安…...

golang 复杂数据结构解析
[{"key":"15275771","pack":{"1":[{"name":"消息配置","id":15275771,"version":1,"createUser":"molaifeng","data":"test"}]},"callback&qu…...

不怕被AirTag跟踪?苹果Find My技术越来越普及
苹果的 AirTag 自推出以来,如何有效遏制用户用其进行非法跟踪,是摆在苹果面前的一大难题。一家为执法部门制造无线扫描设备的公司近日通过 KickStarter 平台,众筹了一款消费级产品,可帮助用户检测周围是否存在追踪的 AirTag 等设备…...
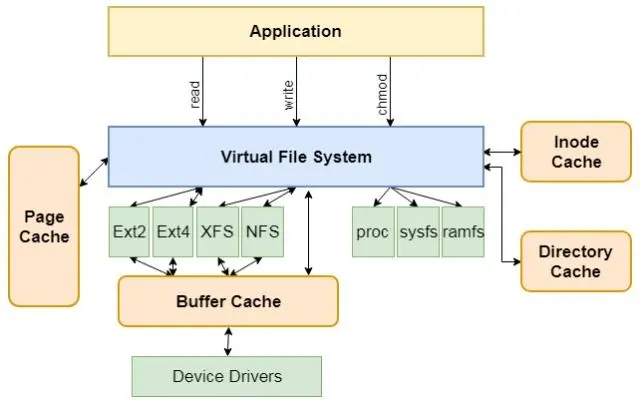
Linux驱动中的open函数是如何从软件打通硬件呢?
一、前言 打开文件是Linux系统中最基本的操作之一,open函数可以实现打开文件的功能。下面我将为您介绍open函数打通上层到底层硬件的详细过程。 二、open函数打通软硬件介绍 open函数是系统调用中的一种,其原型定义在头文件unistd.h中: #…...

Java 基础语法
Java 是一门广泛使用的编程语言,由于其简单易学和可移植性,已成为开发 Web 应用程序、移动应用程序、桌面应用程序以及企业级应用程序的首选语言之一。在本文中,我们将探讨 Java 的基础语法,包括变量、数据类型、运算符、控制流等…...
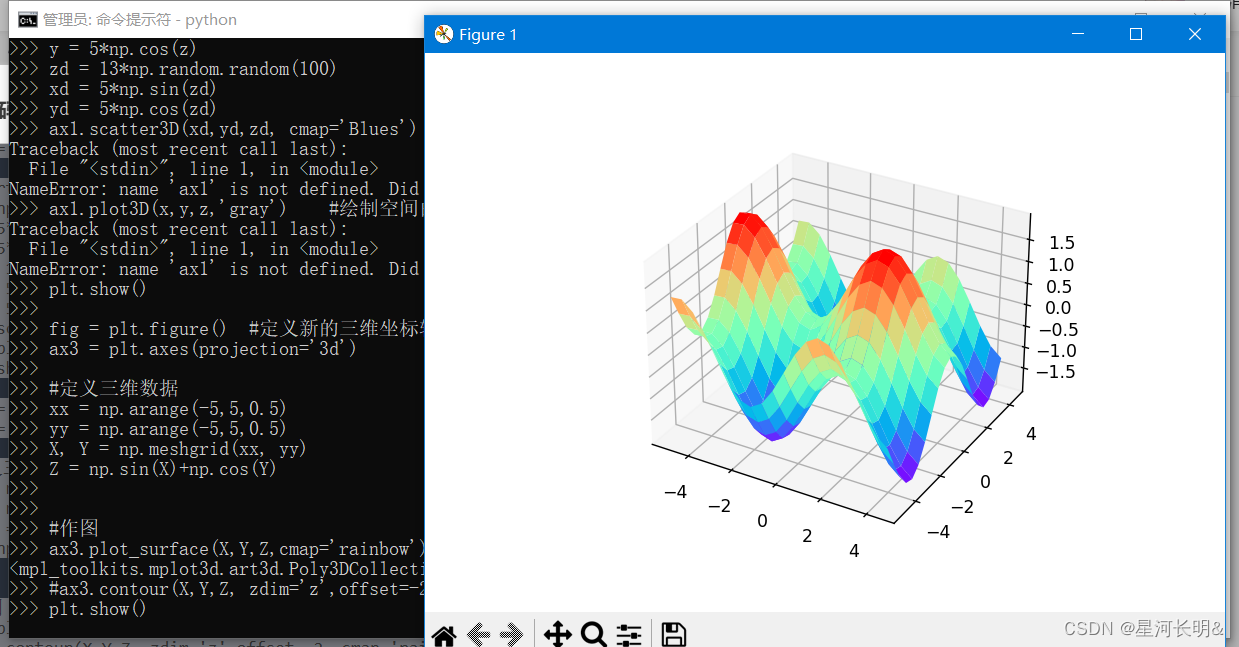
python下如何安装并使用matplotlib(画图模块)
在搜索命令中输入cmd,以管理员身份运行。 输入以下命令,先对pip安装工具进行升级 pip install --upgrade pip 升级完成 之后使用pip安装matplotlib pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple 也可以使用pycharm来安装matp…...

系统分析师---计算机网络思维导图
TCP、IP协议簇(4星) 传输协议:TCP有连接、可靠、有回应机制、三次握手基于TCP的应用层协议:POP3:邮件收取,默认端口110SMTP:邮件发送,默认端口25FTP:文件传输协议&#…...

算法练习(七)数据分类处理
一、数据分类处理 1、题目描述: 信息社会,有海量的数据需要分析处理,比如公安局分析身份证号码、 QQ 用户、手机号码、银行帐号等信息及活动记录。采集输入大数据和分类规则,通过大数据分类处理程序,将大数据分类输出…...

nohup ./startWebLogic.sh >out.log 2>1 解析
在启动weblogic的时候我们经常看到如下的命令: nohup ./startWebLogic.sh >out.log 2>&1 & 从09年开始用weblogic到现在已经过去3年多了 ,今天终于将该命令理解清楚了。 其中 0、1、2分别代表如下含义: 0 – stdin (standa…...
)
OpenCV 坡度计算(基于DEM,C++版本)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 假设一个点位于曲面 z = f ( x , y ) z=f(x,y) z=...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
