【算法】复习搜索与图论
🍎 博客主页:🌙@披星戴月的贾维斯
🍎 欢迎关注:👍点赞🍃收藏🔥留言
🍇系列专栏:🌙 蓝桥杯
🌙请不要相信胜利就像山坡上的蒲公英一样唾手可得,但是请相信,世界上总有一些美好值得我们全力以赴,哪怕粉身碎骨!🌙
🍉一起加油,去追寻、去成为更好的自己!
文章目录
- 前言
- 🍎1.中国象棋中的马的行动
- 题目描述
- 输入格式
- 输出格式
- 🍎2.Dijkstra求最短路 I(图论)
- 题目描述
- 🍎3.Dijkstra求最短路 II
- 🍎4. spfa求最短路
- 🍎总结
提示:以下是本篇文章正文内容,下面案例可供参考
前言
深度遍历算法(depth first search)俗称dfs和 广度优先遍历(broad first search)俗称bfs以及我们常听到的图论里面的最短路问题,借着这篇文章我们一起深入了解一下这些算法的逻辑和解法。
🍎1.中国象棋中的马的行动
题目描述
在中国象棋中,马的行动方式是“日”字形。假设我们有一个 8x8 的棋盘,棋盘的左上角是(0,0),右下角是(7,7)。马开始时位于给定的位置(x,y),你的任务是计算马需要多少步才能到达目标位置(a,b)。如果马不能到达目标位置,就返回-1。
注意:马只能按照“日”字形行动,即先向上或向下移动两步,然后向左或向右移动一步,或者先向左或向右移动两步,然后向上或向下移动一步。
输入格式
输入共两行,每行包含两个整数。第一行是马的初始位置(x,y),第二行是马的目标位置(a,b)。所有的整数都在0到7之间。
输出格式
输出一个整数,表示马到达目标位置需要的最少步数。如果不能到达,就输出-1。
输入输出样例
0 0;
7 7;
输出样例:
6
老规矩, 我们要养成一个好的写程序习惯,那就是先写思路,再写实现过程
解题思路:
首先,我们可以通过看数据范围大致判断这一题用到的算法,数据范围才8,可以支持dfs,bfs,dp等等各种算法,而且我们读题可以知道,🐎的行动方式是“日”字形,即可以画图得出它的方向图

即我们可以设置一个距离数组,通过bfs去枚举这八个方向,算出初始点到各个可能到达点的距离,我们通过队列来存储可能到达的下一个点,如果队列里面没有数字了就代表遍历结束,返回值。
代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
#define x first
#define y second
bool st[10][10];
int d[10][10];
int a1, b1, a2, b2;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
int bfs(int x, int y)
{queue<pii> q;q.push({x, y});//把点放入队列st[x][y] = true;//标记while(q.size()){auto t = q.front();q.pop();if(t.x == a2 && t.y == b2) return d[a2][b2];//如果找到直接返回距离数组for(int i = 0; i < 8; i++){int ax = t.x + dx[i], ay = t.y + dy[i];if(ax < 0 || ax > 7 || ay < 0 || ay > 7 || st[ax][ay] == true) continue;st[ax][ay] = true;d[ax][ay]=d[t.x][t.y]+1;q.push({ax, ay});}}return -1;//如果找不到就返回-1
}
int main ()
{cin >> a1 >> b1;cin >> a2 >> b2;int t = bfs(a1, b1);cout << t << endl; return 0;
}
写法2:dfs深度搜索
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
#define x first
#define y second
bool st[10][10];
int dist[10][10];
int a1, b1, a2, b2;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
void dfs(int x, int y)
{if(x == a2 && y == b2) return;//判断结束条件for(int i = 0; i <= 7; i++){int tx = x + dx[i];int ty = y + dy[i];if(tx < 0 || tx > 7 || ty < 0 || ty > 7)continue;if(dist[tx][ty] > dist[x][y] + 1){dist[tx][ty] = dist[x][y] + 1;dfs(tx, ty);}}return;
}
int main ()
{cin >> a1 >> b1;cin >> a2 >> b2;memset(dist, 0x3f, sizeof dist); //先将方向数组置为0x3fdist[a1][b1] = 0;dfs(a1, b1);if(dist[a2][b2] == 0x3f3f3f3f) cout << "-1" << endl;//如果没有搜到就输出-1else cout << dist[a2][b2] << endl;//否则输出距离return 0;
}
学习搜索我还推荐大家去看走迷宫和红与黑这两题,都是比较经典的。
🍎2.Dijkstra求最短路 I(图论)
题目描述
由于题目复制会乱码,所以博主干脆用图片代替。

图论问题和dp问题的区别
dp是选择下一个数(选择下一个状态)
图论是选择这个小的点去更新后继的节点

如下图例子:
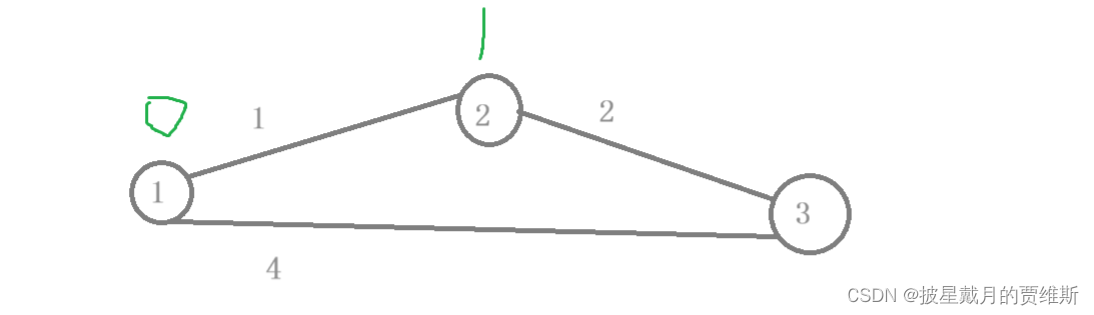
在这个例子中,我们把已经确定的最短的距离标为绿色,这时候我们t = 2这个节点,发现3这个节点 的距离到原点是4大于2 + 1,更新3和节点1的最短距离。
代码示例:
dist数组存储的是第一个节点到第 j个节点的距离是累加的
#include<bits/stdc++.h>
using namespace std;
//存稠密图用邻接矩阵
const int N = 510;
int n, m;
int g[N][N];
int dist[N];
bool st[N];int dijkstar()
{memset(dist, 0x3f, sizeof dist); // 1、先初始化距离dist[1] = 0; //1号点到自己的距离为0for(int i = 0; i < n; i++){int t = -1;for(int j = 1; j <= n; j++) //遍历所有点{if(!st[j] && (t == -1 || dist[t] > dist[j]))//如果j没有遍历过和t == -1或者t这点的距离>j的距离,更新tt = j;}st[t] = true;for(int j = 1; j <= n; j++){dist[j] = min(dist[j], dist[t] + g[t][j]);//g的ab是a 到b 点的距离}}if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];}
int main ()
{ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m; //n个点m条边memset(g, 0x3f, sizeof g);while(m --){int a, b, c;cin >> a >> b >> c;g[a][b] = min(g[a][b], c);}int h = dijkstar();cout << h << endl;return 0;
}
🍎3.Dijkstra求最短路 II
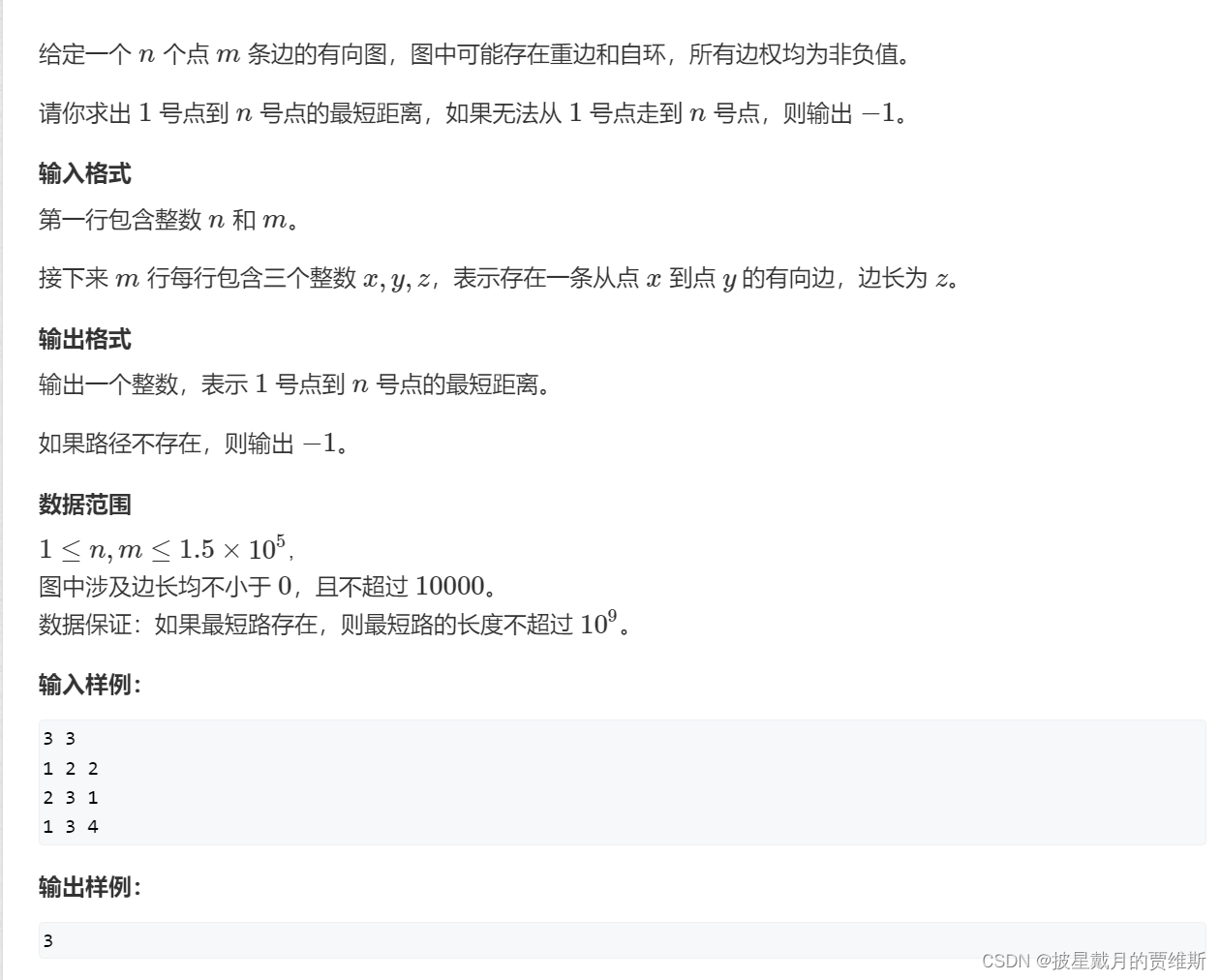
思路:n的数据范围从500 到了 1.5 * 10的五次方,数据量一下子变得很大,用邻接矩阵去存储很容易爆内存,而且会超时,所以要用邻接表去存。而且为了提高效率,我们要用优先级队列。
时间复杂度m*logn
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
#define x first
#define y secondtypedef pair<int, int> pii;
int h[N], ne[N], e[N], idx, w[N];
int n, m;
bool st[N];
int dist[N];
void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] =idx++;
}
int dijkstart()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<pii, vector<pii>, greater<pii>> q;q.push({0, 1}); //1号点,距离是0,编号是1while(q.size()){auto t = q.top();q.pop();int ver = t.y, d = t.x; if(st[ver]) continue; //说明遍历过了st[ver] = true; //标记for(int i = h[ver]; i!= -1; i = ne[i]){int j = e[i];//当前节点if(dist[j] > d + w[i]){dist[j] = d + w[i];q.push({dist[j], j});}}}if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];
}
int main ()
{memset(h, -1, sizeof h);cin >> n >> m;while(m --){int a, b, c;cin >> a >> b >> c;add(a, b, c);}int h = dijkstart();cout << h << endl;return 0;
}🍎4. spfa求最短路
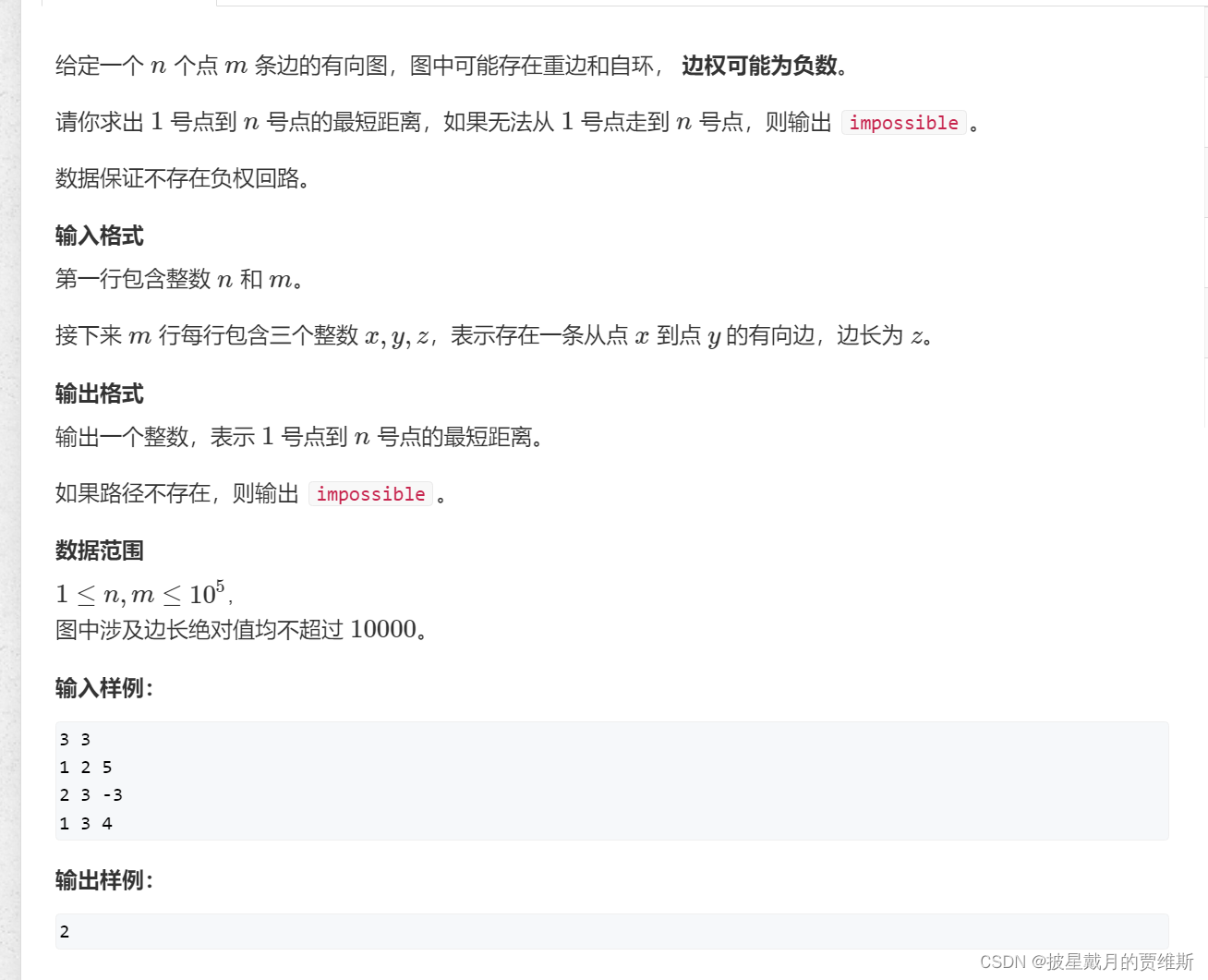
如果说边的距离全部都是正的,我们用dijkstart算法,那么如果存在负边权,那么我们可以采用spfa算法,而且spfa算法效率会高很多,时间复杂度是0(n * m)。同样,我们可以用spfa算法解决之前dijkstart算法的题,spfa的写法很像上一道题,利用邻接表去存储,然后利用队列把距离短的点存储起来,然后去更新后继节点。但是我可能会比较嫌弃邻接表写法比较复杂,我们可以用vector<结构体>这样的形式来存储图。
代码示例:
#include<bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
struct Node
{int node;int w;
};
int dist[N];
bool st[N];vector<Node> g[N];//二维的数组
int spfa()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;queue<int> q; //队列存储所有待更新的点q.push(1); //把1号点放入队列st[1] = true;// st数组存当前这个点是否在队列当中while(q.size()){int t = q.front();//每次取出队头q.pop();st[t] = false;//更新所有领边for(int i = 0; i < g[t].size(); i ++){int j = g[t][i].node;if(dist[j] > dist[t] + g[t][i].w){dist[j] = dist[t] + g[t][i].w;if(!st[j]){q.push(j);st[j] = true;}}}}return dist[n];
}
int main ()
{cin >> n >> m;while(m --){int a, b, c;cin >> a >> b >> c;g[a].push_back({b, c});}int t = spfa();if(t == 0x3f3f3f3f) cout << "impossible";else cout << t << endl;return 0;
}
🍎总结
本文和大家介绍了几题搜索和图论的题目,既帮助了自己复习,也希望对读者有所帮助!
相关文章:

【算法】复习搜索与图论
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙请不要相信胜利就像山坡上的蒲公英一样唾手…...

【KCC@南京】KCC南京数字经济-开源行
一场数字经济与开源的视听盛宴,即将于11月26日,在南京举办。本次参与活动的有: 庄表伟(开源社理事执行长、天工开物开源基金会执行副秘书长)、林旅强Richard(开源社联合创始人、前华为开源专家)…...
苍穹外卖-day11
苍穹外卖-day11 课程内容 Apache ECharts营业额统计用户统计订单统计销量排名Top10 功能实现:数据统计 数据统计效果图: 1. Apache ECharts 1.1 介绍 Apache ECharts 是一款基于 Javascript 的数据可视化图表库,提供直观,生…...

git_07_协同开发
1.作业回复 干的什么事?动了哪些东西? 文档作业xxx文档已编写完成,相关svn目录:xxx/xxx/xxx代码作业(Git代码提交规范)具体什么问题,影响范围,是否已经解决: feat(xxx):改动描述 perf(xxx):改动…...
对比国内主流开源 SQL 审核平台 Yearning vs Archery
Yearning, Archery 和 Bytebase 是目前国内最主流的三个开源 SQL 审核平台。其中 Yearning 和 Archery 是社区性质的项目,而 Bytebase 则是商业化产品。通常调研 Bytebase 的用户也会同时比较 Yearning 和 Archery。 下面我们就来展开对比一下 Yearning 和 Archery…...

Mistral 7B 比Llama 2更好的开源大模型 (三)
Mistral 7B 比Llama 2更好的开源大模型 Mistral 7B是一个70亿参数的语言模型,旨在获得卓越的性能和效率。Mistral 7B在所有评估的基准测试中都优于最好的开放13B模型(Llama 2),在推理、数学和代码生成方面也优于最好的发布34B模型(Llama 1)。Mistral 7B模型利用分组查询注…...
关于 Git 你了解多少?
1. 什么是Git? Git 是一个版本控制系统,由林纳斯托瓦兹创建。它旨在管理项目代码的更改,以便团队成员可以协作开发和维护代码库。Git 可以让用户跟踪代码的更改、回滚错误的更改、合并代码等。Git 还具有分支和标签的功能,使得团队成员可以在…...

关于Elasticsearch的自动补全、数据同步和集群,以下是相关的知识点
1. 自动补全:Elasticsearch可以通过自动补全功能帮助用户快速查找相关的内容。它使用了一种称为“completion suggester”的功能来实现自动补全,是一种基于前缀的建议查询,可以在用户输入时提供实时建议。 2. 数据同步:Elasticse…...
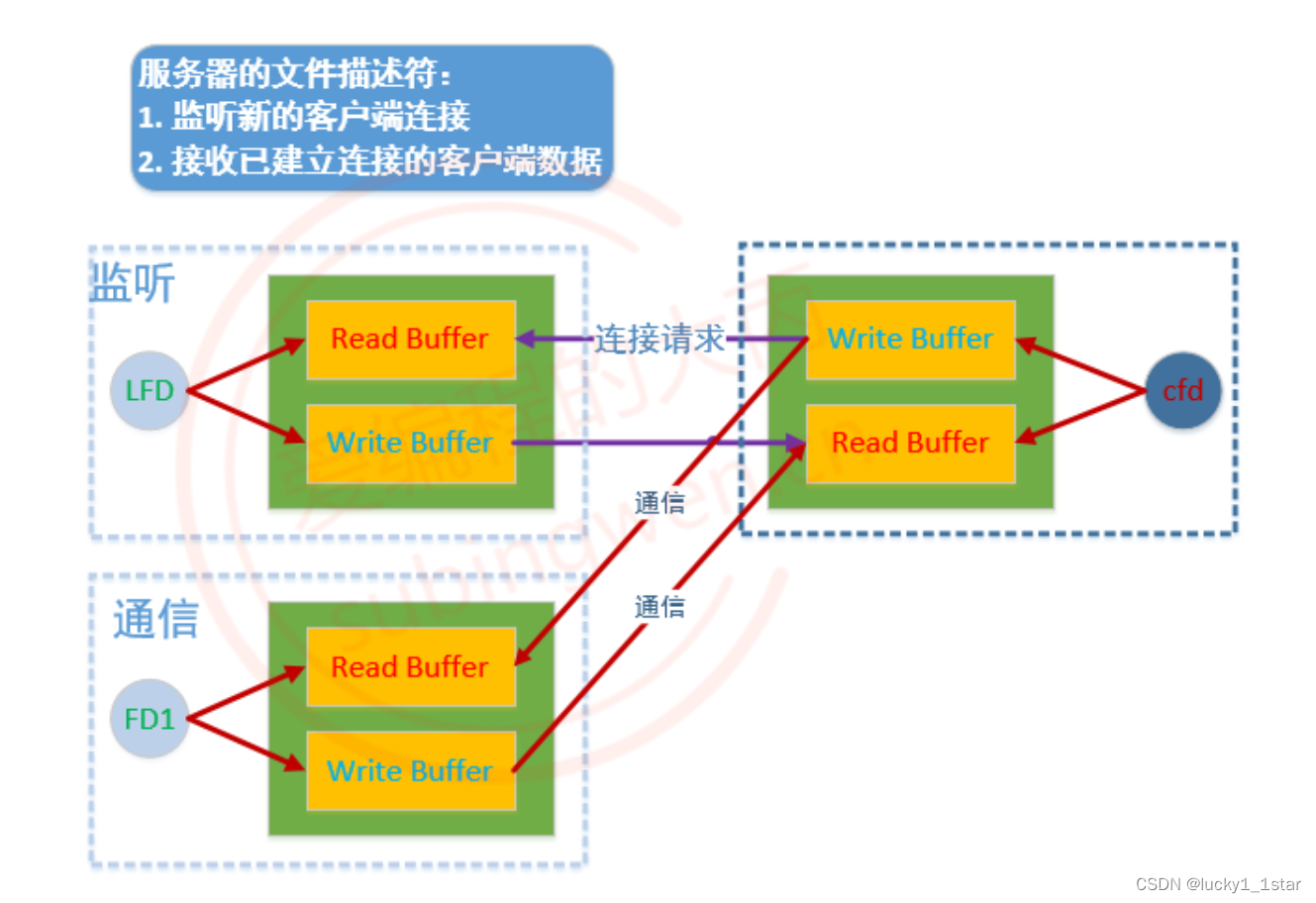
linux套接字-Socket
1.概念 局域网和广域网 局域网:局域网将一定区域内的各种计算机、外部设备和数据库连接起来形成计算机通信的私有网络。广域网:又称广域网、外网、公网。是连接不同地区局域网或城域网计算机通信的远程公共网络。IPInternet Protocol)&#…...
debian 修改镜像源为阿里云【详细步骤】
文章目录 修改步骤第 1 步:安装 vim 软件第 2 步:备份源第 3 步:修改为阿里云镜像参考👉 背景:在 Docker 中安装了 jenkins 容器。查看系统,发现是 debian 11(bullseye)。 👉 目标:修改 debian bullseye 的镜像为阿里云镜像,加速软件安装。 修改步骤 第 1 步:…...

从0到0.01入门React | 004.精选 React 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...
Linux 本地zabbix结合内网穿透工具实现安全远程访问浏览器
前言 Zabbix是一个基于WEB界面的提供分布式系统监视以及网络监视功能的企业级的开源解决方案。能监视各种网络参数,保证服务器系统的安全运营;并提供灵活的通知机制以让系统管理员快速定位/解决存在的各种问题。 本地zabbix web管理界面限制在只能局域…...
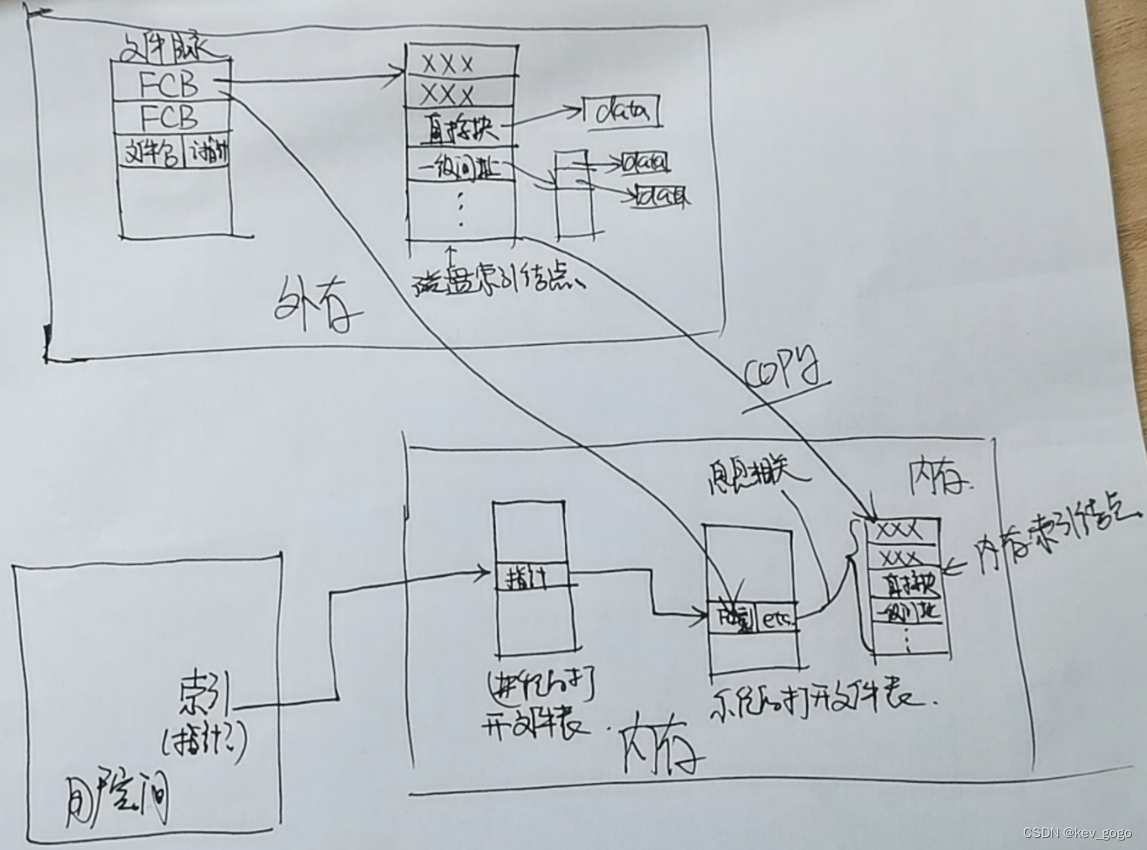
【以图会意】文件系统从外存到内存到用户空间
首先,在文件目录中,装有很多块FCB,由文件名和i指针两部分构成,指针指向文件所在的索引结点,包含了例如:文件存储权限,文件长度等一系列文件的信息,最重要的当然是物理地址࿰…...

一、交换配置
2.SW1、SW2、SW3启用MSTP,实现网络二层负载均衡和冗余备份,创建实例Instance10和Instance20,名称为skills,修订版本为1,其中Instance10关联Vlan60和Vlan70,Instance20关联Vlan80和Vlan90。SW1为Instance0和Instance10的根交换机,为Instance20备份根交换机;SW2为Instanc…...

验证码:EasyDL 机器学习识别与云码平台一站式识别
目录 EasyDL 机器学习识别(实践:京东商城) (一)批量获取验证码图片 (二)EasyDL机器学习(百度智能云) (三)调用EasyDLAPI接口识别验证码 云码…...

postgreSQL中的高速缓存
1. 高速缓存简介 如下图所示,当一个postgreSQL进程读取一个元组时,需要获取表的基本信息(例如:表的oid、索引信息和统计信息等)及元组的模式信息,这些信息被分别记录在多个系统表中。通常一个表的模式信…...

我把MySQL运行在Docker上,差点完了……
容器的定义:容器是为了解决“在切换运行环境时,如何保证软件能够正常运行”这一问题。 目前,容器和 Docker 依旧是技术领域最热门的词语,无状态的服务容器化已经是大势所趋,同时也带来了一个热点问题被大家所争论不以&…...

【华为OD题库-023】文件目录大小-java
题目 一个文件目录的数据格式为:目录id,本目录中文件大小,(子目录id列表)。其中目录id全局唯一, 取值范围[1 ,200],本目录中文件大小范围[1,1000],子目录id列表个数[0,10] 例如: 1 20 (2,3)表示目录1中文件总大小是20,有两个子目录…...
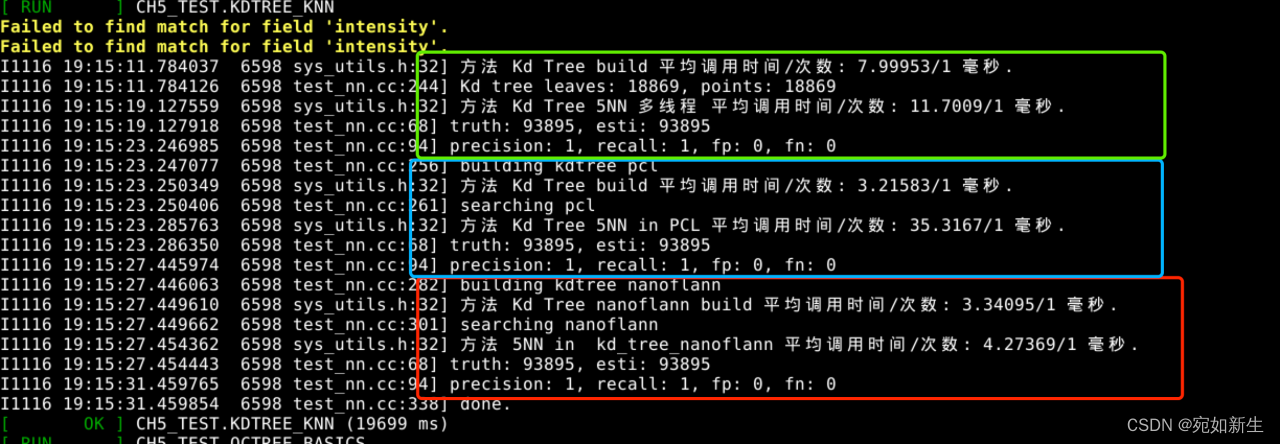
4. 【自动驾驶与机器人中的SLAM技术】点云中的拟合问题和K近邻
目录 1.在三维体素中定义 NEARBY14,实现 14 格最近邻的查找。2.推导arg max||Ad||22的解为ATA的最大特征向量或者奇异向量。3. 将本节的最近邻算法与一些常见的近似最近邻算法进行对比,比如nanoflann,给出精度指标和时间效率指标。4. 也欢迎大…...

正点原子嵌入式linux驱动开发——Linux ADC驱动
在之前的笔记中,学习了如何给ICM20608编写IIO驱动,ICM20608本质就是ADC,因此纯粹的ADC驱动也是IIO驱动框架的。本章就学习一下如何使用STM32MP1内部的ADC,并且在学习巩固一下IIO驱动。 ADC简介 ADC ADC,Analog to D…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
