【深度学习】吴恩达课程笔记(四)——优化算法
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~
【吴恩达课程笔记专栏】
【深度学习】吴恩达课程笔记(一)——深度学习概论、神经网络基础
【深度学习】吴恩达课程笔记(二)——浅层神经网络、深层神经网络
【深度学习】吴恩达课程笔记(三)——参数VS超参数、深度学习的实践层面
吴恩达课程笔记——优化算法
- 八、优化算法
- 1.优化算法介绍
- 2.批量梯度下降(Batch Gradient Descent)
- 目的
- 步骤
- 优点
- 缺点
- 3.随机梯度下降(Stochastic Gradient Descent, SGD)
- 目的
- 步骤
- 优点
- 缺点
- 4.小批量梯度下降(Mini-batch Gradient Descent)
- 目的
- 步骤
- 优点
- 缺点
- 理解
- 如何选择mini-batch size
- 5.指数加权平均数(Exponentially Weighted Averages)
- 目的
- 步骤
- 优点
- 缺点
- 具体加权过程举例
- 指数加权平均的偏差修正
- 6.动量梯度下降法 (Gradient descent of Momentum)
- 目的
- 基本原理
- 7.RMSprop
- 目的
- 优点
- 基本原理
- 8.Adam 优化算法(Adam optimization algorithm)
- 简介
- 工作方式
- 优点
- 算法
- 9.学习率衰减(Learning rate decay)
- 做法
- 几种公式
- 10.局部最优问题
八、优化算法
1.优化算法介绍
当涉及深度学习优化算法时,我们通常会面临一个目标:最小化一个损失函数。这个损失函数衡量了模型预测与实际值之间的差距。为了找到最佳的模型参数,我们需要使用优化算法来调整这些参数,以便最小化损失函数。
以下是一些常用的深度学习优化算法:
- 梯度下降(Gradient Descent):通过计算成本函数相对于参数的梯度,并沿着梯度的反方向更新参数,以最小化成本函数。
- 随机梯度下降(Stochastic Gradient Descent, SGD):与梯度下降类似,但是每次迭代中只使用一个样本来计算梯度,这在大型数据集上更有效。
- 小批量梯度下降(Mini-batch Gradient Descent):结合了批量梯度下降和随机梯度下降的优点,每次迭代使用一小批样本来计算梯度。
- 指数加权平均数( Exponentially weighted averages):常用于计算梯度的指数加权平均或者计算参数的指数加权平均。
- 动量梯度下降法 (Gradient descent of Momentum) :梯度下降算法的一种改进版本,它结合了梯度下降和动量的概念。
- RMSProp:通过考虑梯度的平方的指数衰减平均值来调整学习率,以应对Adagrad的学习率急剧下降问题。
- Adam 优化算法(Adam optimization algorithm) :在训练神经网络时有效地调整参数,并能够适应不同参数的变化情况,结合了动量梯度下降法和RMSProp算法。
- 学习率衰减(Learning rate decay) :在训练神经网络时逐渐降低学习率的过程。
这些算法都有各自的优劣势,适用于不同类型的深度学习任务。在实际应用中,通常需要根据具体问题和数据集的特点来选择合适的优化算法。
2.批量梯度下降(Batch Gradient Descent)
目的
批量梯度下降是为了优化模型参数,使得损失函数达到最小值,从而实现训练数据的拟合和模型的泛化能力。
步骤
-
初始化参数:随机初始化模型参数或采用预训练的参数作为初始值。
-
对于整个训练样本集合进行如下操作:
-
计算梯度:计算损失函数关于所有训练样本的参数的梯度,即
∇ J ( θ ) = 1 m ∑ i = 1 m ∇ J ( θ ; x ( i ) , y ( i ) ) \nabla J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \nabla J(\theta; x^{(i)}, y^{(i)}) ∇J(θ)=m1i=1∑m∇J(θ;x(i),y(i)) -
更新参数:利用所有训练样本的梯度信息,按照梯度下降的更新规则来更新模型参数:
θ = θ − η ⋅ ∇ J ( θ ) \theta = \theta - \eta \cdot \nabla J(\theta) θ=θ−η⋅∇J(θ)
其中, ( η ) 是学习率, ( m ) 是训练样本的数量。
-
优点
- 可以保证收敛性,即在合理的学习率下,批量梯度下降一定可以找到全局最优解或局部最优解。
缺点
- 当训练样本很大时,计算所有训练样本的梯度会非常耗时,尤其在内存有限的情况下。
- 对于大规模数据集,批量梯度下降的计算效率较低。
3.随机梯度下降(Stochastic Gradient Descent, SGD)
目的
随机梯度下降(Stochastic Gradient Descent, SGD)是梯度下降法的一种变种
通过每次迭代仅利用单个训练样本的梯度信息,来更新模型参数,从而减少计算开销,并加快收敛速度。
步骤
-
初始化参数:随机初始化模型参数或采用预训练的参数作为初始值。
-
对于每个训练样本 (x(i), y(i)) 进行如下操作:
-
计算梯度:计算损失函数关于当前样本的参数的梯度,即
∇ J ( θ ; x ( i ) , y ( i ) ) \nabla J(\theta; x^{(i)}, y^{(i)}) ∇J(θ;x(i),y(i))
-
更新参数:利用当前样本的梯度信息,按照梯度下降的更新规则来更新模型参数:
θ = θ − η ⋅ ∇ J ( θ ; x ( i ) , y ( i ) ) \theta = \theta - \eta \cdot \nabla J(\theta; x^{(i)}, y^{(i)}) θ=θ−η⋅∇J(θ;x(i),y(i))
其中,( η )是学习率。
-
优点
- 减少计算开销:由于每次仅利用单个样本来更新参数,相比批量梯度下降,SGD在计算上更为高效。
- 适用于大规模数据集:特别适用于大规模数据集,因为每次迭代只需要处理一个样本。
缺点
- 不稳定性:由于每次迭代仅利用单个样本,使得更新方向带有较大的随机性,可能导致收敛过程不稳定。
- 学习率调整困难:学习率的选择对于SGD的影响较大,需要谨慎调整。
4.小批量梯度下降(Mini-batch Gradient Descent)
目的
小批量梯度下降是为了优化模型参数,使得损失函数达到最小值,从而实现训练数据的拟合和模型的泛化能力。
步骤
-
初始化参数:随机初始化模型参数或采用预训练的参数作为初始值。
-
对于每个小批量样本(x(i), y(i)) 进行如下操作:
-
计算梯度:计算损失函数关于当前小批量样本的参数的梯度,即
1 m ∑ i = 1 m ∇ J ( θ ; x ( i ) , y ( i ) ) \frac{1}{m} \sum_{i=1}^{m} \nabla J(\theta; x^{(i)}, y^{(i)}) m1i=1∑m∇J(θ;x(i),y(i)) -
更新参数:利用当前小批量样本的梯度信息,按照梯度下降的更新规则来更新模型参数:
θ = θ − η ⋅ 1 m ∑ i = 1 m ∇ J ( θ ; x ( i ) , y ( i ) ) \theta = \theta - \eta \cdot \frac{1}{m} \sum_{i=1}^{m} \nabla J(\theta; x^{(i)}, y^{(i)}) θ=θ−η⋅m1i=1∑m∇J(θ;x(i),y(i))
其中, ( η ) 是学习率, ( m ) 是小批量样本的大小。
-
优点
- 小批量梯度下降结合了梯度下降和随机梯度下降的优点,可以更快地收敛到局部最优解。
- 可以充分利用矩阵运算的并行性,提高计算效率。
缺点
- 需要调节的超参数更多,如学习率 ( η ) 和小批量样本的大小 ( m )。
- 需要对数据进行分批处理,增加了实现的复杂性。
理解
定义梯度下降时使用一次全部样本集合为一代。
- batch梯度下降的 J 会不断下降;mini-batch梯度下降的 J 不一定会不断下降,但是整体呈现下降趋势。

-
两者都需要多次遍历全部数据集才会有效果。在mini-batch中,如果只经历一代,那么梯度下降的效果虽然比batch一代好,但总体效果仍是微小的。
-
使用mini-batch时,每重新开始遍历一次数据集,应当把数据集中的数据重新打乱分配到mini-batch中,体现出随机性
如何选择mini-batch size
- 小训练集:使用batch gradient decent(m less than 2000)
- 通常的minibatch size:64、128、256、512、1024
5.指数加权平均数(Exponentially Weighted Averages)
目的
指数加权平均数用于对时间序列数据进行平滑处理,以便观察数据的长期趋势。
步骤
假设给定一个序列 ( x1, x2, …, xt ),其指数加权平均数 ( vt ) 的计算方式为:
v t = β v t − 1 + ( 1 − β ) x t v_t = \beta v_{t-1} + (1-\beta) x_t vt=βvt−1+(1−β)xt
( 0 < 𝛽 < 1 ) 被称为平滑因子,较大的平滑因子意味着新观测值对平均数的影响更大,从而使得平均数更快地适应最新的观测值;而较小的平滑因子则意味着平均数更加稳定、更不容易受到新观测值的影响。
( v0 ) 可以被初始化为 0 或者 x1 ,为了在开始时确定初始的指数加权平均数值
优点
- 对不同时刻的数据赋予不同的权重,更加灵活地适应数据变化。
- 计算高效,每次更新只需要一次乘法和一次加法运算。
缺点
- 对于某些特定类型的数据,可能对异常值(outliers)过于敏感,从而影响平均值的准确性。
具体加权过程举例

假设英国去年第t天的气温是θt

要用一条曲线拟合温度变化,可以进行如下操作
v 0 = 0 v t = β v t − 1 + ( 1 − β ) θ t v_0=0 \\ v_t=\beta v_{t-1}+(1-\beta)\theta_t v0=0vt=βvt−1+(1−β)θt
其中 vt 是第t天附近的 1/(1-𝛽) 天的平均天气。
为什么这么规定?
( 1 − ε ) 1 / ε 约等于 1 e (数学中一个挺重要的数) 这说明 1 1 − β 天之外的数所占的权重总共不到 1 e ,不那么值得关注了 (1-ε)^{1/ε}约等于\frac{1}{e}(数学中一个挺重要的数)\\ 这说明\frac{1}{1-\beta}天之外的数所占的权重总共不到\frac{1}{e},不那么值得关注了 (1−ε)1/ε约等于e1(数学中一个挺重要的数)这说明1−β1天之外的数所占的权重总共不到e1,不那么值得关注了
β = 0.9 ( 1 − 0.1 ) 1 0.1 = 0. 9 10 β = 0.98 ( 1 − 0.02 ) 1 0.02 = 0.9 8 50 \beta = 0.9\\ (1-0.1)^{\frac{1}{0.1}} = 0.9^{10} \\ \beta = 0.98 \\ (1-0.02)^{\frac{1}{0.02}} = 0.98^{50} β=0.9(1−0.1)0.11=0.910β=0.98(1−0.02)0.021=0.9850
可以看出 𝛽 越大,平均的天数越大,拟合得越粗略。

红色:𝛽=0.9;绿色:𝛽=0.98
指数加权平均的偏差修正

由于v0=0,v1=𝛽 v0 + (1-𝛽) θ1 = (1-𝛽)θ1,前几个vi的值会非常的小,如图中紫线。当迭代到一定数量之后,拟合才变得正常(紫线逼近绿线)。
偏差修正的目的是为了消除初始时刻的平均值对整体平均值的影响。偏差修正可以通过以下公式实现:
v t ^ = v t 1 − α t v t ^ 表示经过偏差修正后的平均值 v t 表示未经修正的平均值 β 为平滑因子 t 表示时间步 \hat{v_t} = \frac{v_t}{1 - \alpha^t} \\ \hat{v_t} 表示经过偏差修正后的平均值\\ v_t 表示未经修正的平均值\\ \beta 为平滑因子\\ t 表示时间步\\ vt^=1−αtvtvt^表示经过偏差修正后的平均值vt表示未经修正的平均值β为平滑因子t表示时间步
通过偏差修正,可以有效地减小最初几个数据点对平均值的影响,得到更加准确和稳定的指数加权平均值。
6.动量梯度下降法 (Gradient descent of Momentum)
目的
加速梯度下降过程
基本原理
传统的梯度下降法在更新参数时只考虑当前的梯度值,而动量梯度下降法引入了一个额外的动量项,用于模拟物理中的动量效应。
在每次参数更新时,动量梯度下降法会根据当前梯度和上一次的动量来计算一个更新量,并将该更新量应用于参数。更新量由两部分组成:一部分是当前梯度的方向,另一部分是上一次动量的方向。

蓝线是一般梯度下降的成本函数值迭代情况,红线是动量梯度下降法中成本函数迭代境况。
我们使用指数加权平均来计算新的dW和db。在竖直方向上,由于平均值接近0,所以动量梯度下降的竖直方向迭代值接近0 。在水平方向上,动量梯度下降的迭代值则为正常水平。
d w = β ⋅ d w t − 1 + ( 1 − β ) ⋅ ∂ J ∂ w d b = β ⋅ d b t − 1 + ( 1 − β ) ⋅ ∂ J ∂ b w = w − α ⋅ d w b = b − α ⋅ d b dw = \beta \cdot dw_{t-1} + (1 - \beta) \cdot \frac{\partial J}{\partial w}\\ db = \beta \cdot db_{t-1} + (1 - \beta) \cdot \frac{\partial J}{\partial b}\\ w = w - \alpha \cdot dw\\ b = b - \alpha \cdot db\\ dw=β⋅dwt−1+(1−β)⋅∂w∂Jdb=β⋅dbt−1+(1−β)⋅∂b∂Jw=w−α⋅dwb=b−α⋅db
β 是动量系数 , 通常取 0.9 α 是学习率 J 是损失函数 d w t − 1 和 d b t − 1 表示上一次的权重和偏置更新量 ∂ J ∂ w 和 ∂ J ∂ b 分别是损失函数对权重和偏置的偏导数 w 和 b 分别表示更新后的权重和偏置 \beta 是动量系数,通常取0.9\\ \alpha 是学习率\\ J 是损失函数\\ dw_{t-1} 和 db_{t-1} 表示上一次的权重和偏置更新量\\ \frac{\partial J}{\partial w} 和 \frac{\partial J}{\partial b} 分别是损失函数对权重和偏置的偏导数\\ w 和 b 分别表示更新后的权重和偏置 β是动量系数,通常取0.9α是学习率J是损失函数dwt−1和dbt−1表示上一次的权重和偏置更新量∂w∂J和∂b∂J分别是损失函数对权重和偏置的偏导数w和b分别表示更新后的权重和偏置
7.RMSprop
目的
解决传统梯度下降法中学习率衰减过快的问题。RMSprop通过对梯度的平方进行指数加权移动平均来调整学习率,从而加速模型的训练。
优点
使用它的时候可以适当加大学习率
基本原理

如图,我们不想要绿线,而想要蓝线。
我们需要计算一个额外变量S,S等于目前数据附近水平方向或竖直方向的dX的方差。
我们在更新数据(W、b)的时候,把原来要减掉的dX除以这个方差,那么方差大的方向变化量就减少,方差小的方向变化量就仍处于正常水平甚至增大。
8.Adam 优化算法(Adam optimization algorithm)
简介
adam是训练神经网络中最有效的优化算法之一。它结合了momentum和RMSprop。
工作方式
- 计算上一个梯度的指数加权平均,存储在v中。
- 计算上一个梯度指数加权平均的平方,存储在s中。
- 使用adam的规则更新参数。
优点
- 通常比较节省内存(尽管还是比GD和momentum多)
- 即使在低学习率条件下也能运行得很好
算法
{ v d W [ l ] = β 1 v d W [ l ] + ( 1 − β 1 ) ∂ J ∂ W [ l ] v d W [ l ] c o r r e c t e d = v d W [ l ] 1 − ( β 1 ) t s d W [ l ] = β 2 s d W [ l ] + ( 1 − β 2 ) ( ∂ J ∂ W [ l ] ) 2 s d W [ l ] c o r r e c t e d = s d W [ l ] 1 − ( β 1 ) t W [ l ] = W [ l ] − α v d W [ l ] c o r r e c t e d s d W [ l ] c o r r e c t e d + ε l = 1 , . . . , L \begin{cases} v_{dW^{[l]}} = \beta_1 v_{dW^{[l]}} + (1 - \beta_1) \frac{\partial \mathcal{J} }{ \partial W^{[l]} } \\ v^{corrected}_{dW^{[l]}} = \frac{v_{dW^{[l]}}}{1 - (\beta_1)^t} \\ s_{dW^{[l]}} = \beta_2 s_{dW^{[l]}} + (1 - \beta_2) (\frac{\partial \mathcal{J} }{\partial W^{[l]} })^2 \\ s^{corrected}_{dW^{[l]}} = \frac{s_{dW^{[l]}}}{1 - (\beta_1)^t} \\ W^{[l]} = W^{[l]} - \alpha \frac{v^{corrected}_{dW^{[l]}}}{\sqrt{s^{corrected}_{dW^{[l]}}} + \varepsilon} \end{cases} \\ l = 1, ..., L ⎩ ⎨ ⎧vdW[l]=β1vdW[l]+(1−β1)∂W[l]∂JvdW[l]corrected=1−(β1)tvdW[l]sdW[l]=β2sdW[l]+(1−β2)(∂W[l]∂J)2sdW[l]corrected=1−(β1)tsdW[l]W[l]=W[l]−αsdW[l]corrected+εvdW[l]correctedl=1,...,L
其中:
- t是adam进行到的步数
- L是神经网络的层数
- 𝛽1(建议使用0.9)和 𝛽2(建议使用0.999)是控制两个指数加权平均的
- α 是学习率
- ε 是一个用来放置分母为0的值很小的数
9.学习率衰减(Learning rate decay)
做法
在不同的代(epoch)上使用递减的学习率
几种公式
α = 1 1 + d e c a y r a t e ∗ e p o c h n u m ∗ α 0 α = a e p o c h n u m ∗ α 0 α = k e p o c h n u m ∗ α 0 手动调整 α 的值 \alpha=\frac{1}{1+decayrate*epochnum}*\alpha_0 \\ \alpha=a^{epochnum}*\alpha_0 \\ \alpha=\frac{k}{\sqrt{epochnum}}*\alpha_0 \\ 手动调整\alpha的值 α=1+decayrate∗epochnum1∗α0α=aepochnum∗α0α=epochnumk∗α0手动调整α的值
10.局部最优问题
- 在神经网络规模较大、参数较多的时候,实际上很难达到局部最优点,更有可能达到的是鞍点。因此梯度下降被困在局部最优点不是很大的问题。
- 鞍点会减缓学习速度,而momentum、RMSprop、Adam正式可以解决这种问题

相关文章:

【深度学习】吴恩达课程笔记(四)——优化算法
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~ 【吴恩达课程笔记专栏】 【深度学习】吴恩达课程笔记(一)——深度学习概论、神经网络基础 【深度学习】吴恩达课程笔记(二)——浅层神经网络、深层神经网络 【深度学习】吴恩达课程笔记(三)——参数VS超参数、深度…...

MyBatis-plus 代码生成器配置
数据库配置(DataSourceConfig) 基础配置 属性说明示例urljdbc 路径jdbc:mysql://127.0.0.1:3306/mybatis-plususername数据库账号rootpassword数据库密码123456 new DataSourceConfig.Builder("jdbc:mysql://127.0.0.1:3306/mybatis-plus","root","…...
框架设计的核心要素
我们的框架应该给用户提供哪些构建产物?产物的模块格式如何?当用户没有以预期的方式使用框架时,是否应该打印合适的警告信息从而提供更好的开发体验,让用户快速定位问题?开发版本的构建和生产版本的构建有何区别&#…...
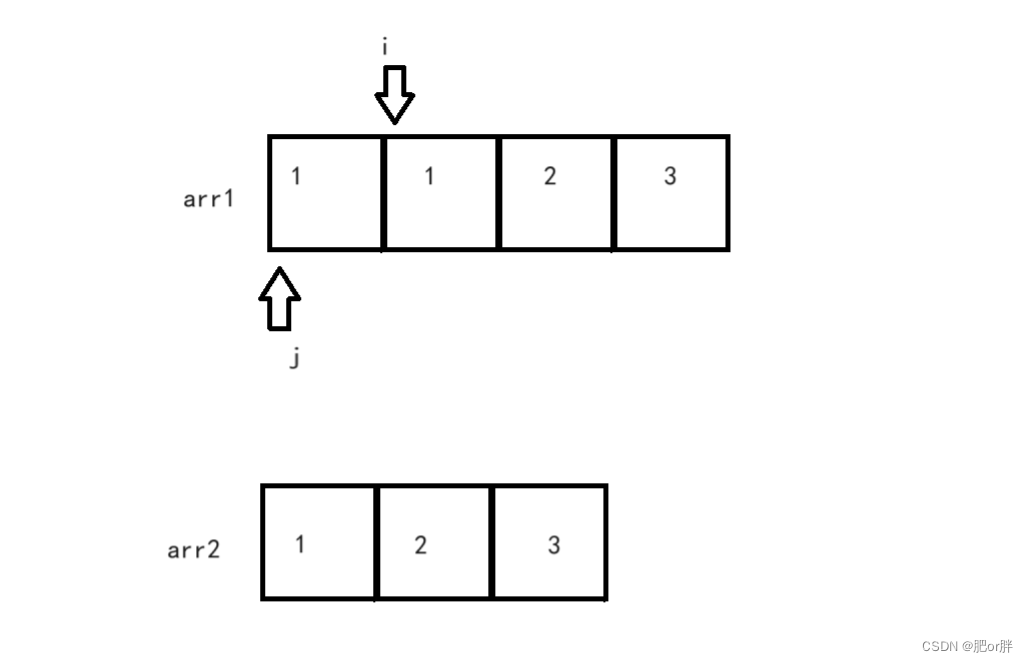
LeetCode - 26. 删除有序数组中的重复项 (C语言,快慢指针,配图)
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 思路一:快慢指针 在数组中,快慢指针就是两个整数下标,定义 fast 和 slow 这里我们从下标1开始(下标0的数据就1个,没有重复项)&…...

C#不安全代码
在C#中,“不安全代码”(unsafe code)通常指的是那些直接操作内存地址的代码。它允许开发者使用指针等低级别的数据结构,这些在通常的安全代码(safe code)中是不允许的。C# 的不安全代码提供了一种方式&…...

《C++避坑神器·二十二》VS能正常运行程序,但运行exe程序无响应解决办法
原因是某个文件只是放在了项目路径下,没有放在exe路径下,比如Json文件原来只放在了mlx项目下,导致VS可以运行,但运行exe无响应或报错如下: 两种方式修改: 1、把Json文件拷贝一份放到exe路径下 2、利用生成…...

lua调用C/C++的函数,十分钟快速掌握
系列文章目录 lua调用C\C动态库函数 系列文章目录摘要环境使用步骤你需要有个lua环境引入库码代码lua代码 摘要 在现代软件开发中,Lua作为一种轻量级脚本语言,在游戏开发、嵌入式系统等领域广泛应用。Lua与C/C的高度集成使得开发者能够借助其灵活性和高…...

自定义GPT已经出现,并将影响人工智能的一切,做好被挑战的准备了吗?
原创 | 文 BFT机器人 OpenAI凭借最新突破:定制GPT站在创新的最前沿。预示着个性化数字协助的新时代到来,ChatGPT以前所未有的精度来满足个人需求和专业需求。 从本质上讲,自定义GPT是之前的ChatGPT的高度专业化版本或代理,但自定…...
vue中一个页面引入多个相同组件重复请求的问题?
⚠️!!!此内容需要了解一下内容!!! 1、会使用promise??? 2、 promise跟 async 的区别??? async 会终止后面的执行,后续…...

Uniapp连接iBeacon设备——实现无线定位与互动体验(实现篇)
export default { data() { return { iBeaconDevices: [], // 存储搜索到的iBeacon设备 deviceId: [], data: [], url: getApp().globalData.url, innerAudioContext: n…...

【ceph】ceph集群删除pool报错: “EPERM: pool deletion is disabled“
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

【微信小程序】使用npm包
1、小程序对npm的支持与限制2、Vant Weapp通过 npm 安装修改 app.json修改 project.config.json构建 npm 包 3、使用4、定制全局主题样式5、API Promise化 1、小程序对npm的支持与限制 目前,小程序中已经支持使用npm安装第三方包, 从而来提高小程序的开发…...

【开发记录篇】第二篇:SQL创建分区表
实现分区表注意事项 分区字段必须在主键中存在 使用时间分区时,字段类型不支持 timestamp,需改为 datetime 年分区示例 下表中使用 insert_time 时间进行分区 CREATE TABLE t_log (id bigint(20) unsigned NOT NULL AUTO_INCREMENT COMMENT 日志ID,inse…...

vue 使用 this.$router.push 传参数,接参数的 query或params 两种方法示例
背景:vue项目 使用this.$router.push进行路由跳转时,可以通过query或params参数传递和接收参数。 通过query参数传递参数: // 传递参数 this.$router.push({path: /target,query: {id: 1,name: John} }); // 接收参数 this.$route.query.id …...
rk3588 usb网络共享连接
出门在外总会遇到傻 X 地方 没有能连接公网的 网口给香橙派连网 而我的香橙派5plus 没有wifi模块。。。话不多说 在手机上看一眼手机的mac地址, 在rk3588 上执行以下命令: sudo ifconfig usb0 down sudo ifconfig usb0 hw ether 58:F2:FC:5D:D4:7A //该m…...

shell 拒绝恶意连接脚本 centos7.x拒绝恶意连接脚本
1. crontab -l 脚本频率: */2 * * * * /bin/bash /home/shell/deny.sh 2. 脚本: rm -rf /home/shell/ip_list cat /var/log/secure | grep "Failed password for" | awk {print$(NF-3)} | sort | uniq -c > /home/shell/ip_list #cat /va…...

【系统架构设计】计算机公共基础知识: 2 计算机系统基础知识
目录 一 计算机系统组成 二 操作系统 三 文件系统 四 系统性能 一 计算机系统组成...
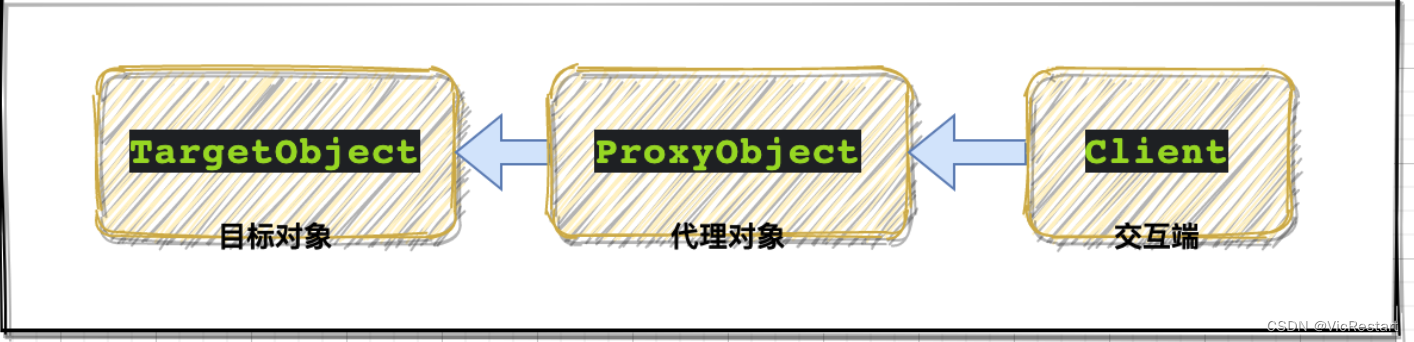
什么是代理模式,用 Python 如何实现 Proxy(代理 或 Surrogate)对象结构型模式?
什么是代理模式? 代理(Proxy)是一种结构型设计模式,其目的是通过引入一个代理对象来控制对另一个对象的访问。代理对象充当目标对象的接口,这样客户端就可以通过代理对象间接地访问目标对象,从而在访问过程…...
国内领先的五大API接口供应商
API(Application Programming Interface)接口,现在很多应用系统中常用的开放接口,对接相应的系统、软件功能,简化专业化的程序开发。作者用过的国内比较稳定的API接口供应商有如下几家,大家可以参考选择&am…...

第十九章 Java绘图
一,Java绘图类 19.1.1Graphics类 Graphics类是所有图形上下文的抽象基类,它允许应用程序在组件以及闭屏图像上进行绘制。 可实现直线,矩形,多边形,椭圆,圆弧等形状和文本,图片的绘制制作。 …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
