c++汉诺塔问题
汉诺塔问题是一个经典的递归问题。基本规则是,给定三个柱子和一些不同大小的盘子,开始时所有盘子按大小顺序堆叠在第一个柱子上,目的是将所有盘子移动到第三个柱子上,并且在移动过程中只能在柱子之间移动一个盘子,并且大盘子不能放在小盘子上面。
以下是一个C++程序示例,用于解决汉诺塔问题:
- #include <iostream>
- using namespace std;
- void hanoi(int n, char from, char inter, char to) {
- if (n == 1) {
- cout << "Move disk 1 from " << from << " to " << to << endl;
- } else {
- hanoi(n - 1, from, to, inter);
- cout << "Move disk " << n << " from " << from << " to " << to << endl;
- hanoi(n - 1, inter, from, to);
- }
- }
- int main() {
- int n;
- cout << "Enter the number of disks: ";
- cin >> n;
- hanoi(n, 'A', 'B', 'C');
- return 0;
- }
在此示例中,hanoi函数使用递归来解决问题。 main函数从用户获取盘子的数量,并调用hanoi函数以解决汉诺塔问题。
当调用hanoi函数时,它将盘子数量n和三个柱子的标识符作为参数传递。 如果n等于1,则函数将打印将盘子从第一个柱子移动到第三个柱子的消息。 否则,函数将递归地调用自身三次,分别将前n-1个盘子从第一个柱子移动到第二个柱子,将第n个盘子从第一个柱子移动到第三个柱子,然后将前n-1个盘子从第二个柱子移动到第三个柱子。
通过这种方式,每个盘子都将被移动到第三个柱子上,并且每个盘子的移动都将遵循汉诺塔问题的规则。
下面是一个示例输出,其中将3个盘子从柱子A移动到柱子C:
- Enter the number of disks: 3
- Move disk 1 from A to C
- Move disk 2 from A to B
- Move disk 1 from C to B
- Move disk 3 from A to C
- Move disk 1 from B to A
- Move disk 2 from B to C
- Move disk 1 from A to C
在这个例子中,每个盘子的移动都遵循汉诺塔问题的规则,并且所有盘子都被成功地从第一个柱子移动到第三个柱子。
相关文章:

c++汉诺塔问题
汉诺塔问题是一个经典的递归问题。基本规则是,给定三个柱子和一些不同大小的盘子,开始时所有盘子按大小顺序堆叠在第一个柱子上,目的是将所有盘子移动到第三个柱子上,并且在移动过程中只能在柱子之间移动一个盘子,并且…...
前端---CSS的样式汇总
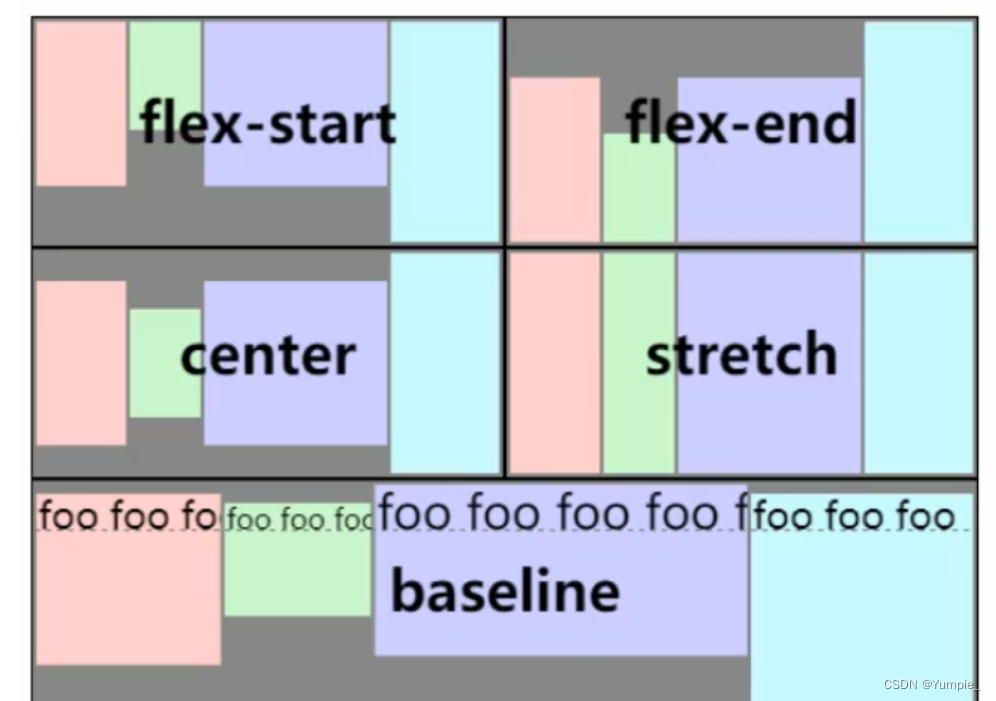
文章目录 CSS的样式元素的属性设置字体设置文字的粗细设置文字的颜色文本对齐文本修饰文本缩进行高设置背景背景的颜色背景的图片图片的属性平铺位置大小 圆角矩形 元素的显示模式行内元素和块级元素的转化弹性布局水平方向排列方式:justify-content垂直方向排序方式…...
android适配鸿蒙系统开发
将一个Android应用迁移到鸿蒙系统需要进行细致的工作,因为两者之间存在一些根本性的差异,涉及到代码、架构、界面等多个方面的修改和适配。以下是迁移工作可能涉及的一些主要方面,希望对大家有所帮助。北京木奇移动技术有限公司,专…...

golang学习笔记——select 判断语句
判断语句 Go 语言提供了以下几种条件判断语句: 语句描述if 语句if 语句 由一个布尔表达式后紧跟一个或多个语句组成。if…else 语句if 语句 后可以使用可选的 else 语句, else 语句中的表达式在布尔表达式为 false 时执行。if 嵌套语句你可以在 if 或 else if 语句…...

FLMix: 联邦学习新范式——局部和全局的结合
文章链接:Federated Learning of a Mixture of Global and Local Models 发表期刊(会议): ICLR 2021 Conference(机器学习顶会) 目录 1. 背景介绍2. 传统联邦学习3. FL新范式理论逻辑重要假设解的特性 本博客从优化函…...
为什么嵌入式没有35岁危机?
为什么嵌入式没有35岁危机? 在当今数字化时代,IT行业变化迅速,技术的更新迭代速度惊人。然而,有一个技术领域却能够在这个竞争激烈的行业中稳步前行,而且不受35岁危机所困扰,那就是嵌入式技术。 嵌入式技术是指将计算…...

PostgreSQL设置主键从1开始自增
和MySQL不同,在 PostgreSQL 中,设置主键从1开始自增并重新开始自增是通过序列(sequence)来实现的。以下是步骤: 步骤1:创建一个序列 CREATE SEQUENCE your_table_id_seqSTART 1INCREMENT 1MINVALUE 1MAXV…...

Vue数据绑定
在我们Vue当中有两种数据绑定的方法 1.单向绑定 2.双向绑定 让我为大家介绍一下吧! 1、单向绑定(v-bind) 数据只能从data流向页面 举个例子: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"…...
js写轮播图,逐步完善
目录 1、自动轮播 2、点击更换 3、自动播放加左右箭头点击切换 4、完整版轮播图 1、自动轮播 用定时器setInterval()来写,可以实现自动播放 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><met…...
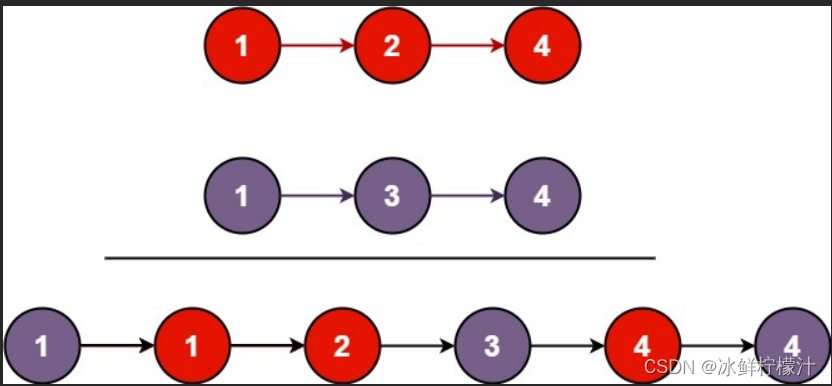
算法-链表-简单-相交、反转、回文、环形、合并
记录一下算法题的学习5 在写关于链表的题目之前,我们应该熟悉回忆一下链表的具体内容 什么是链表: 链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,…...
【500强 Kubernetes 课程】第3章 运行docker容器
一 - 三 ,docker基础操作见 第2章7节 四、docker部署web网站 1、安装 nginx (适合场景:学习 - 略) 2、docker 安装 nginx Stage 1 :docker hub 上 搜索 nginx 镜像 Stage 2:拉取官方镜像 Stage 3&…...

Python中表格插件Tabulate的用法
目录 一、引言 二、Tabulate插件安装与导入 三、Tabulate基本用法 1、创建表格: 2. 格式化表格: 3. 表格转置: 4、合并单元格: 5、指定每列的格式: 6、指定每行的格式: 7、使用自定义表格格式&am…...
)
缺陷分级(过程质量bug分级)
缺陷按照其影响的严重程度,从高到低分成5级,分别为致命(Blocker)、严重(Critical)、一般(Major)、轻微(Minor)以及建议(Enhancement)。…...
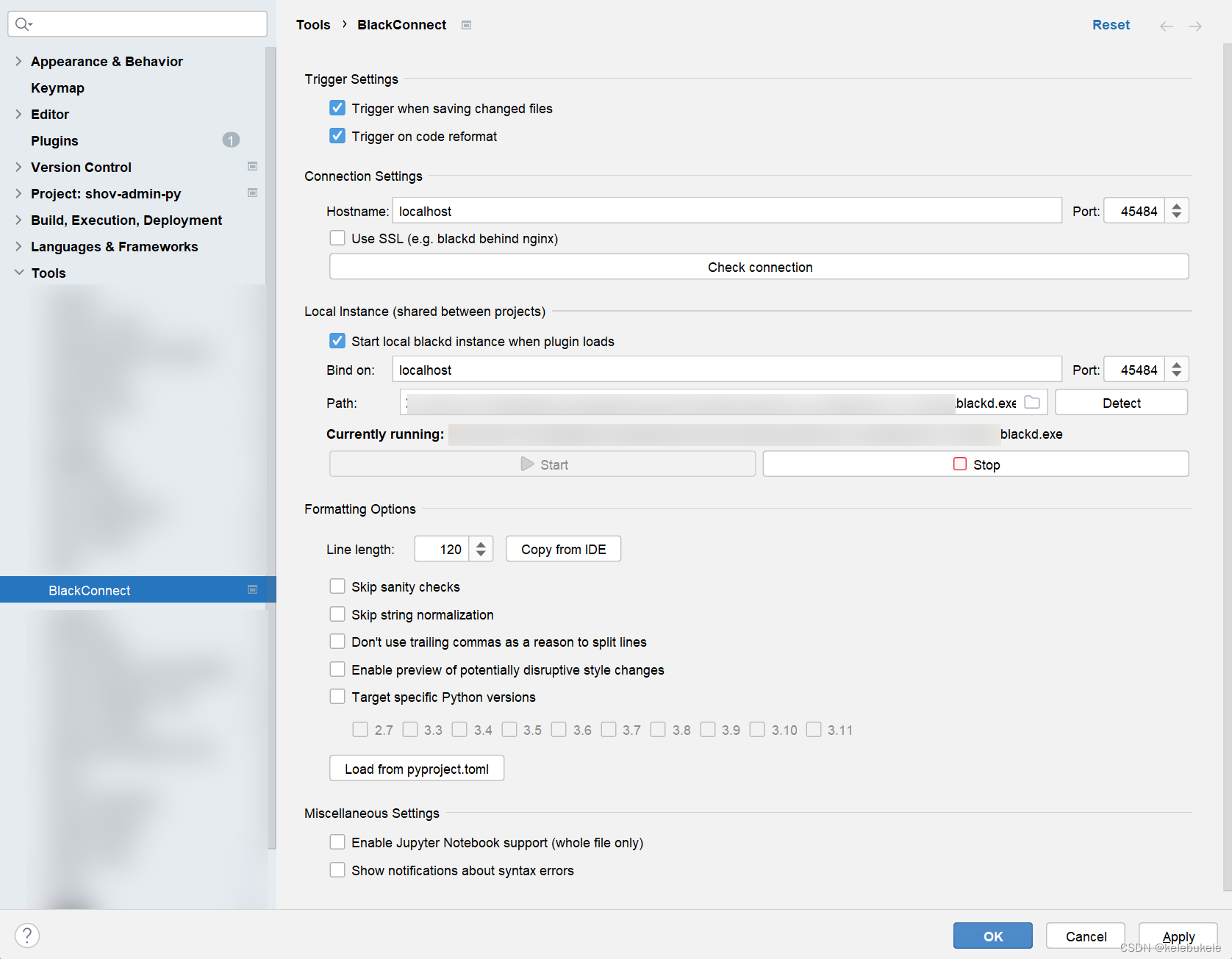
pycharm/vscode 配置black和isort
Pycharm blackd Pycharm中有插件可以实现后台服务运行black:BlackConnect 安装 在python中安装blackd 配置 Pycharm isort pycharm中,isort没有插件,暂使用外部工具实现,外部工具也可添加快捷键实现快捷对文件、文件夹进行fo…...

python列出本地文件路径
按照之前的设想,如果要罗列出本地文件的列表,那不是需要不断的判断文件夹里面的文件夹吗?或者需要使用递归函数本身,才能达到目的吧?没想到使用pop这个函数就可以了。pop是取出元素,那列表里就少了一个&…...

在JavaScript中检查一个数字是否是另一个数字的倍数
使用%模数运算符 为了检查一个数字是否是另一个数字的倍数,我们可以使用JavaScript中的% modulo运算符。 modulo% 操作符返回第一个数字在第二个数字上的余数,例如:10 % 2 0 ,所以如果我们得到一个余数0 ,那么给定的数…...
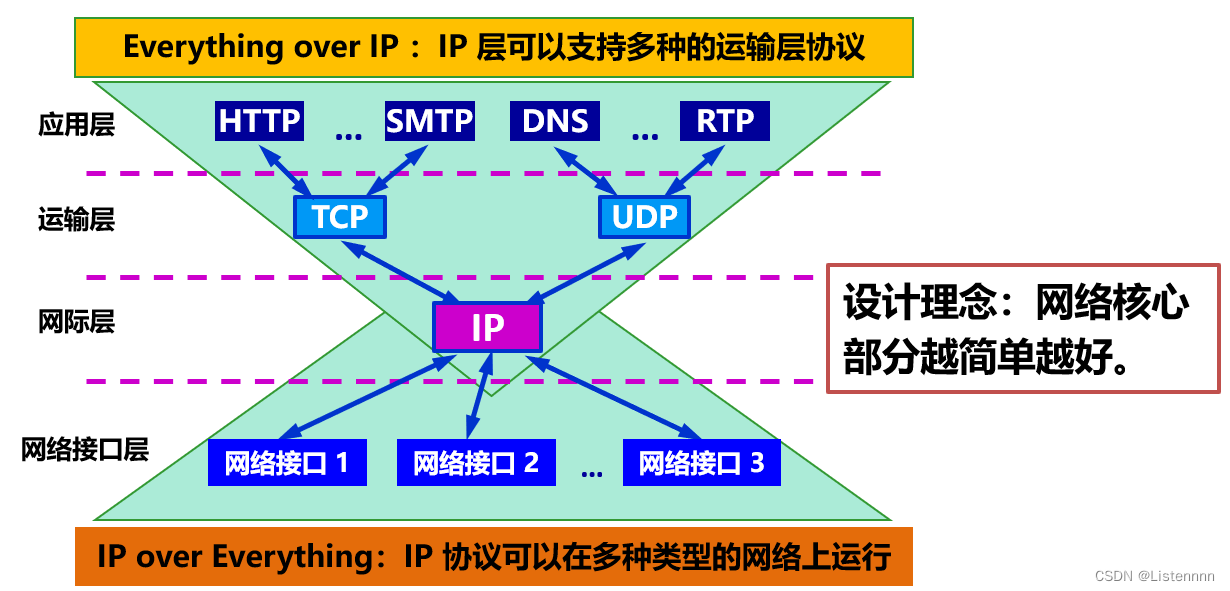
计算机网络五层协议的体系结构
计算机网络中两个端系统之间的通信太复杂,因此把需要问题分而治之,通过把一次通信过程中涉及的所有问题分层归类来进行研究和处理 体系结构是抽象的,实现是真正在运行的软件和硬件 1.实体、协议、服务和服务访问点 协议必须把所有不利条件和…...

MySQL 运算符二
逻辑运算符 逻辑运算符用来判断表达式的真假。如果表达式是真,结果返回 1。如果表达式是假,结果返回 0。 运算符号作用NOT 或 !逻辑非AND逻辑与OR逻辑或XOR逻辑异或 1、与 mysql> select 2 and 0; --------- | 2 and 0 | --------- | 0 | -…...

【SA8295P 源码分析】121 - MAX9295A 加串器芯片手册分析 及初始化参数分析
【SA8295P 源码分析】121 - MAX9295A 加串器芯片手册分析 及初始化参数分析 一、MAX9295A 芯片特性1.1 GPIO 引脚说明1.2 功能模块框图1.3 时序分析1.3.1 GMSL2 Lock Time:25 ms1.3.2 视频初始化延时:1.1ms + 17000 x t(PCLK)1.3.3 High-Speed Data Transmission in Bursts1.…...

问题汇总20231103
文章目录 前言问题汇总1.所有操作系统在CPU层面上是不是都为时间片轮转的形式处理程序?只是任务调度的调度算法不同?那多线程的本质也是时间片吗?只不过很小?2.Mcu和mpu的本质区别3.下载HAL库步骤4.RAM,ROM,SRAM,SDRAM,DDR内存5.编…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
