向量以及矩阵
0.前言
好了那我们新的征程也即将开始,那么在此呢我也先啰嗦两句,本篇文章介绍数学基础的部分,因为个人精力有限我不可能没一字一句都讲得非常清楚明白,像矩阵乘法之类的一些基础知识我都是默认你会了(还不会的同学推荐去b站上一套课程:线性代数(mit的公开课版本)),就比如这篇文章的写作目的也只是带大家回顾一下后续我们敲代码需要使用的一些前置知识,当然我会在这些前置知识当中加入自己独特的见解,这也应该也是本个系列最有意思的地方。
1.向量
1.1什么是向量?
在数学中,向量是具有大小和方向的量。它可以表示为有序的数字集合,通常以列向量或行向量的形式表示。

上述图其实就能很好的概括我高中学过的一些基础知识。(我们高中学的模其实就是这里的长度,只是在图形学的领域我们会用两个绝对值来表示)
1.2平行四边形法则以及常用的一些表达

如上图所示,在我们在平面内进行基本的向量合成的时候,四边形法则无疑能很好的帮助我们。(这里向量与向量之间的最基本运算就不提了)
上图需要注意的是我们的采用矩阵的形式来指代了向量。
1.3点乘
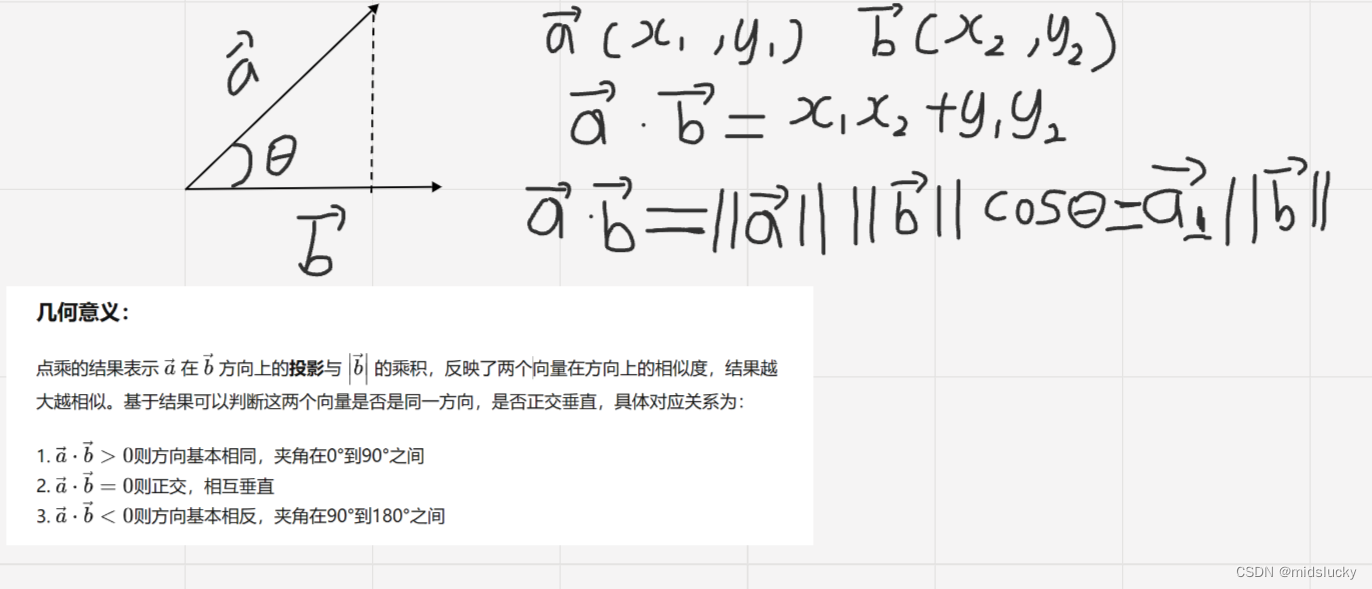

ok那基本上对点乘有了这些认知后就足够了。
1.4叉乘

基本上这副图就能囊括我所想要表达的一切,当然其公式的推导与证明过于繁杂就不在这里进行展开了。
简单的应用
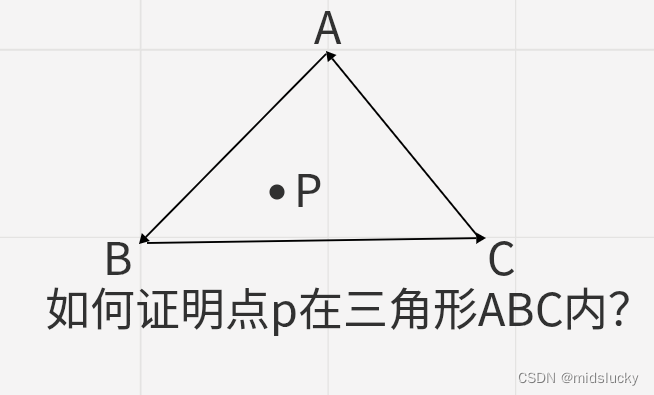
这个问题非常简单,只需要分别证明p分别在AB向量的右侧,在BC向量的左侧,AC向量的左侧(用叉乘得到的正负在加上右手螺旋法则即可)
(如果我此刻换成了以左手定则为标准会怎么样?这样的话我们上面定义的叉乘这一套就行不通了,因为上面的那一套都是以右手坐标系来定义的,如果定义成了左手坐标系,我们可以在右手所使用的计算规则上最后加个负号来得到左手坐标系下的运算值)
2.矩阵
2.1一些基础知识的回顾
(如果手上有资料的同学可以去翻看一下有关矩阵乘法的笔记)

当然有关这块内容这边也不做太多的解释只是带着大家回顾一下一些常用的,默认大家是有一定线代基础的。
2.2向量点乘与叉乘 和 矩阵乘法的一些关系

相关文章:

向量以及矩阵
0.前言 好了那我们新的征程也即将开始,那么在此呢我也先啰嗦两句,本篇文章介绍数学基础的部分,因为个人精力有限我不可能没一字一句都讲得非常清楚明白,像矩阵乘法之类的一些基础知识我都是默认你会了(还不会的同学推…...
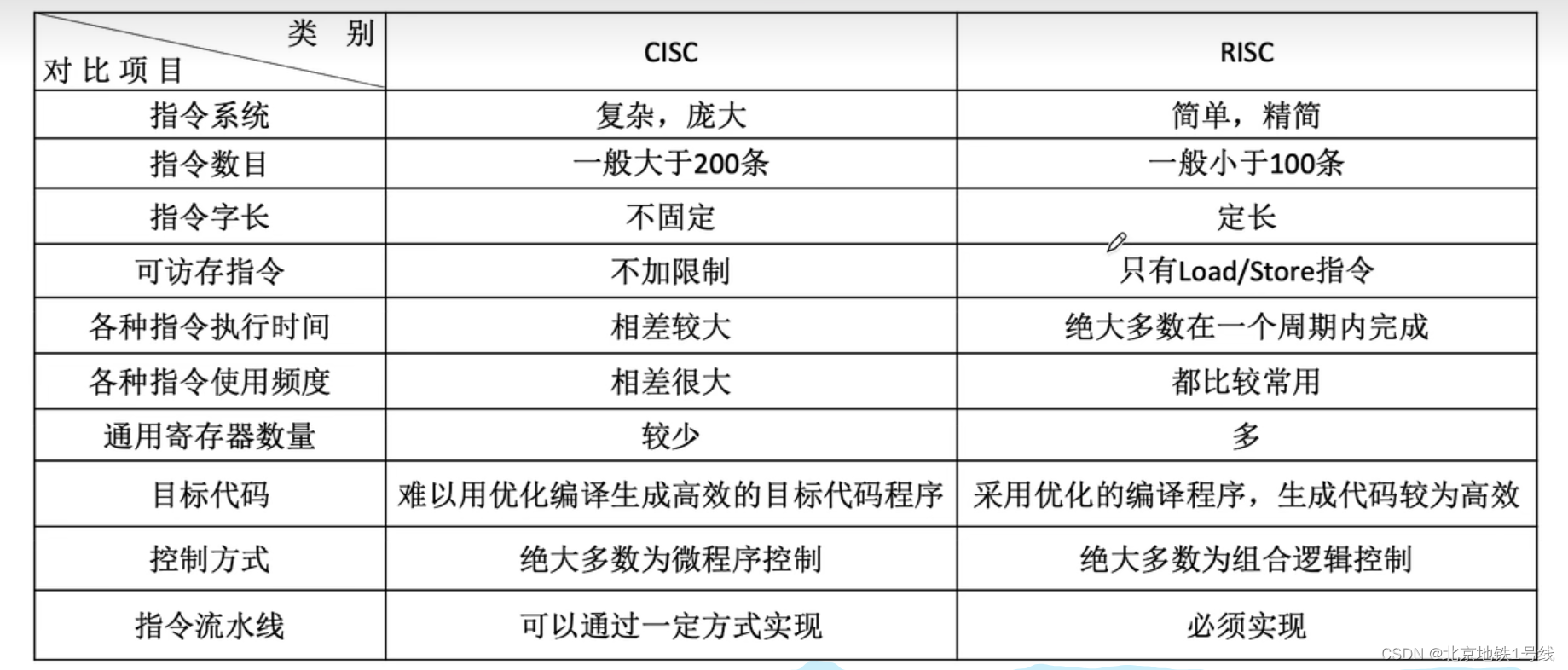
9.程序的机器级代码表示,CISC和RISC
目录 一. x86汇遍语言基础(Intel格式) 二. AT&T格式汇编语言 三. 程序的机器级代码表示 (1)选择语句 (2)循环语句 (3)函数调用 1.函数调用命令 2.栈帧及其访问 3.栈帧的…...

《硅基物语.AI写作高手:从零开始用ChatGPT学会写作》《从零开始读懂相对论》
文章目录 《硅基物语.AI写作高手:从零开始用ChatGPT学会写作》内容简介核心精华使用ChatGPT可以高效搞定写作的好处如下 《从零开始读懂相对论》内容简介关键点书摘最后 《硅基物语.AI写作高手:从零开始用ChatGPT学会写作》 内容简介 本书从写作与ChatG…...

【2016年数据结构真题】
已知由n(M>2)个正整数构成的集合A{a<k<n},将其划分为两个不相交的子集A1 和A2,元素个数分别是n1和n2,A1和A2中的元素之和分别为S1和S2。设计一个尽可能高效的划分算法,满足|n1-n2|最小且|s1-s2|最大。要求…...
创作者等级终于升到4级了
写了两个月的文章,终于等到4级了。发文纪念一下:...
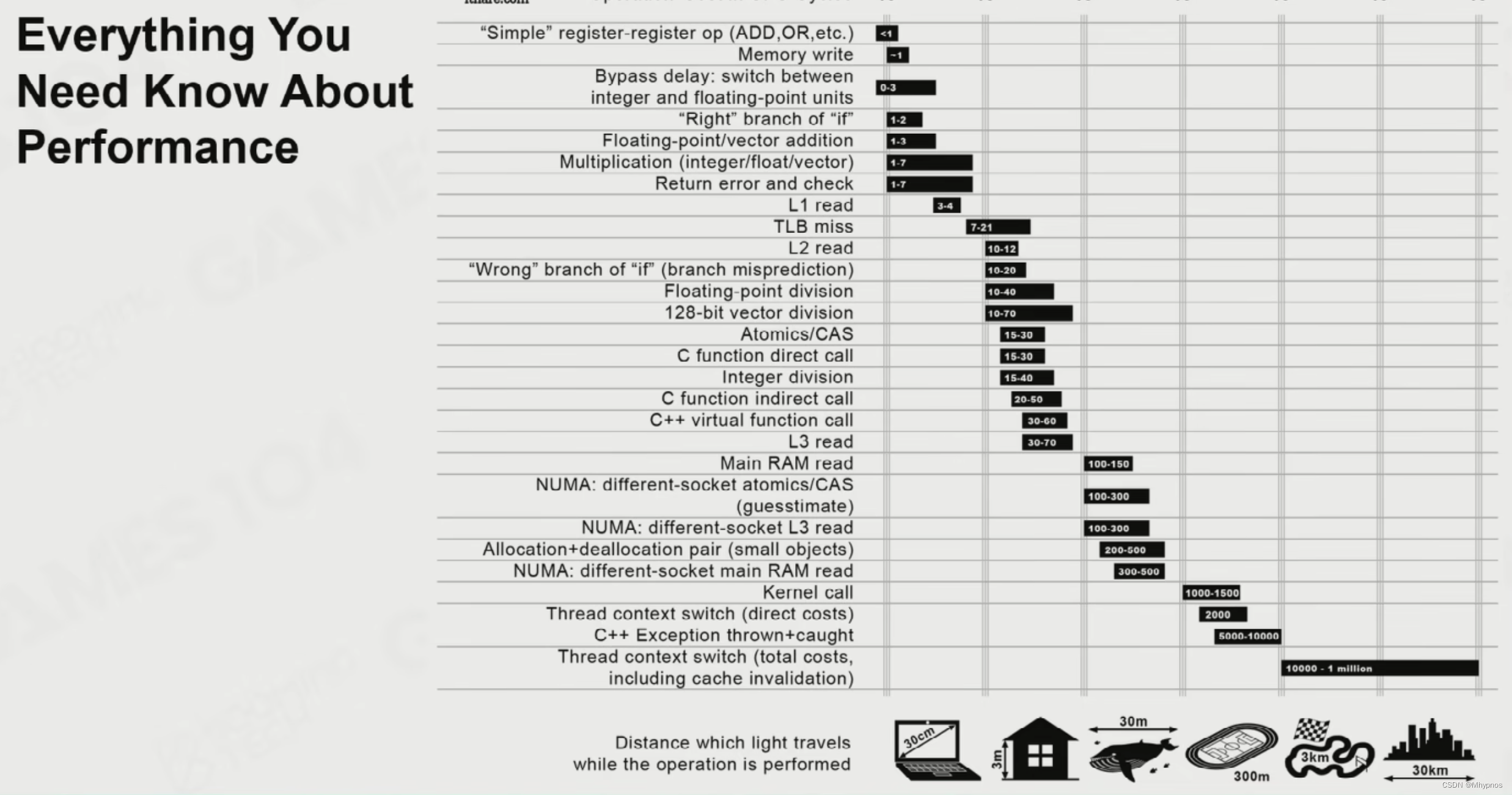
Games104现代游戏引擎笔记 面向数据编程与任务系统
Basics of Parallel Programming 并行编程的基础 核达到了上限,无法越做越快,只能通过更多的核来解决问题 Process 进程 有独立的存储单元,系统去管理,需要通过特殊机制去交换信息 Thread 线程 在进程之内,共享了内存…...
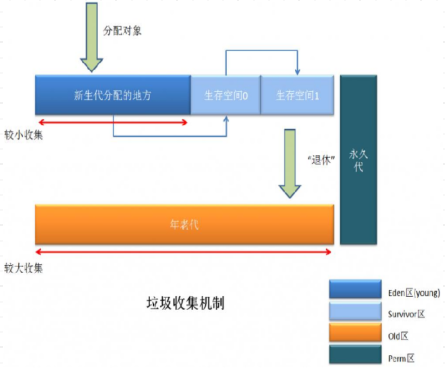
系列三、GC垃圾回收【总体概览】
一、GC垃圾回收【总体概览】 JVM进行GC时,并非每次都对上面的三个内存区域(新生区、养老区、元空间/永久代)一起回收,大部分回收的是新生区里边的垃圾,因此GC按照回收的区域又分为了两种类型,一种是发生在新…...
WPA破解-创建Hash-table加速并用Cowpatty破解)
无线WiFi安全渗透与攻防(N.3)WPA破解-创建Hash-table加速并用Cowpatty破解
WPA破解-创建Hash-table加速并用Cowpatty破解 WPA破解-创建Hash-table加速并用Cowpatty破解1.Cowpatty 软件介绍2.渗透流程1.安装CoWPAtty2.抓握手包1.查看网卡2.开启监听模式3.扫描wifi4.抓握手包5.进行冲突模式攻击3.STA重新连接wifi4.渗透WPA wifi5.使用大字典破解3.hash-ta…...

golang 动态库
目录 1. golang 动态库2. golang 语言使用动态库、调用动态链接库2.1. Go 插件系统2.2. 动态加载的优劣2.3. Go 的插件系统:Plugin2.4. 插件开发原则2.4.1. 插件独立2.4.2. 使用接口类型作为边界2.4.3. Unix 模块化原则2.4.4. 版本控制 2.5. 插件开发示例2.5.1. 编写…...

Python的2042小游戏及其详解
源码: import random import os# 游戏界面尺寸 SIZE 4# 游戏结束标志 GAME_OVER False# 初始化游戏界面 board [[0] * SIZE for _ in range(SIZE)]# 随机生成一个初始方块 def add_random_tile():empty_tiles [(i, j) for i in range(SIZE) for j in range(SIZ…...
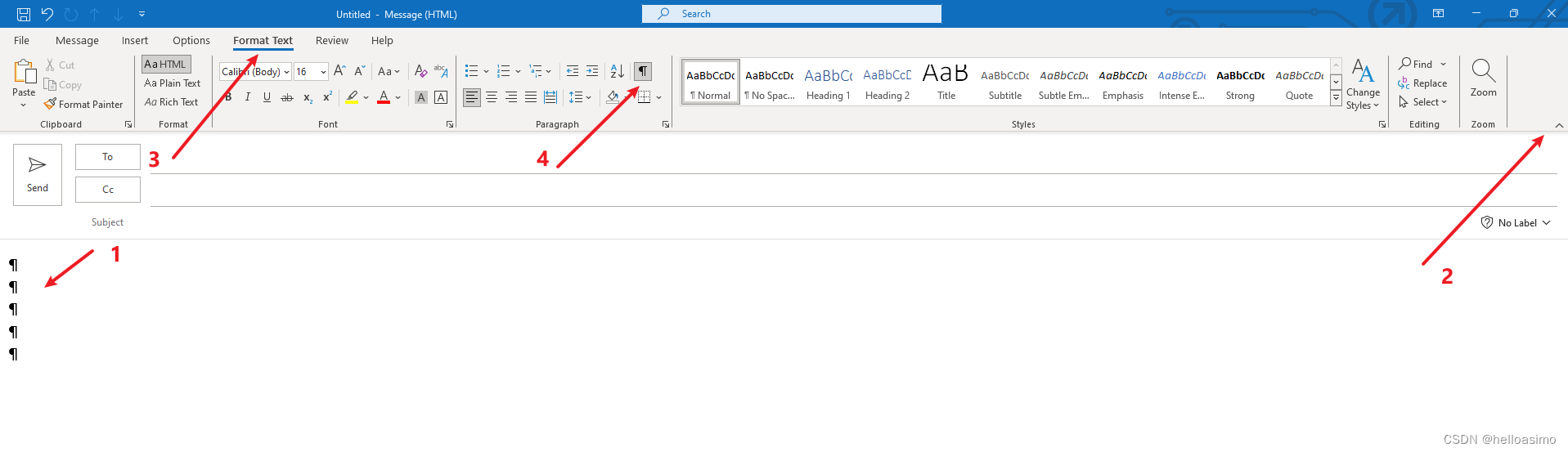
怎么去掉邮件内容中的回车符
上图是Outlook 截图,可见1指向的总有回车符; 故障原因: 不小心误按了箭头4这个选项; 解决方法: 点击2箭头确保tab展开; 点击3以找到箭头4. 取消勾选或者多次点击,即可解决。...
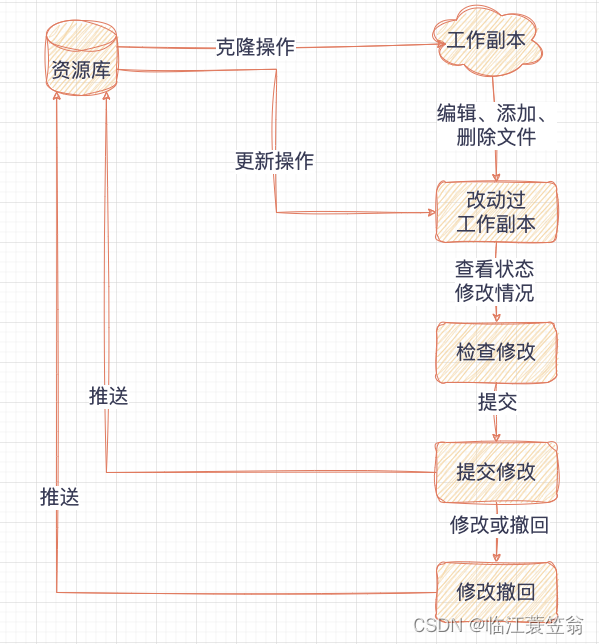
Git-概念与架构
GIT-概念与架构 一、背景和起源二、版本控制系统1.版本控制分类1.1 集中式版本控制1.2 分布式版本控制 2.Git和SVN对比2.1 SVN2.2 GIT 三、GIT框架1.工作区(working directory)2.暂存区(staging area)3.本地仓库(local…...

android 数独小游戏 经典数独·休闲益智
一款经典数独训练app 标题资源下载 (0积分)https://download.csdn.net/download/qq_38355313/88544810 首页页面: 1.包含有简单、普通、困难、大师四种难度的数独挑战供选择; 记录页面: 1.记录用户训练过的数独信息&…...

GAT里面的sofamax函数的实现:
1.sofamx 公式: 2. GAT里的sofamax函数的实现: 1. 因为指数在x轴正轴爆炸式地快速增长,如果zi比较大,exp(zi)也会非常大,得到的数值可能会溢出。溢出又分为下溢出(Underflow)和上溢出&#x…...
Idea 编译SpringBoot项目Kotlin报错/Idea重新编译
原因应该是一次性修改了大量的文件, SpringBoot项目启动Kotlin报错, Build Project也是同样的结果, 报错如下 Error:Kotlin: Module was compiled with an incompatible version of Kotlin. The binary version of its metadata is 1.9.0, expected version is 1.1.13. Build-&…...
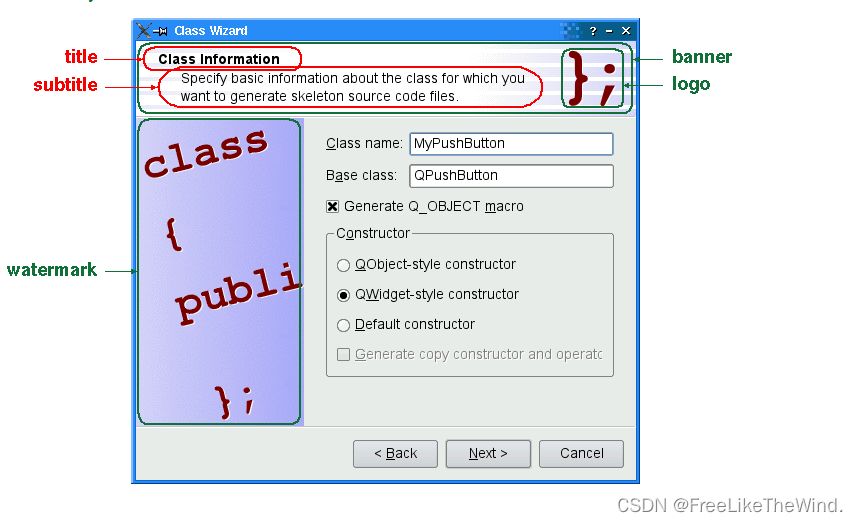
【Qt之QWizard问题】setPixmap()设置logo、background、watermark无效不显示解决方案
问题原因: 使用QWizard或者QWizardPage设置像素图,结果设置完不显示效果。 设置示例: setPixmap(QWizard::WatermarkPixmap, QPixmap("xxx/xxx/xxx.png"));setPixmap(QWizard::BackgroundPixmap, QPixmap("xxx/xxx/xxx.png&…...

mysql 设置远程登录
为了允许远程连接到MySQL服务器,你需要采取以下步骤: 编辑MySQL配置文件: 打开MySQL的配置文件 my.cnf 或 my.ini,这取决于你的操作系统和MySQL版本。该文件通常位于MySQL安装目录下的 etc 或 etc/mysql 目录中。 添加或确保以下行…...

ES的索引概念
1. 概念:Elasticsearch(ES)是一个开源的全文搜索引擎,可以快速地存储、搜索和分析大量的结构化和非结构化数据。 2. 索引的作用:ES索引是将数据存储在Elasticsearch中的基本方式。它用于存储、搜索、分析和查询数据。…...

text/xml和application/xml
困惑 在http消息中,同样是传送xml信息,有的时候看到Content-Type的值是text/xml,有的时候值是application/xml,感到困惑。 例如,用Postman发送http消息给Tomcat中的基于JAX-WS的 web服务: 请求中传送了xm…...

鸿蒙4.0正式版升级机型
官网支持升级机型入口:HarmonyOS 4支持机型 | 华为官网 (huawei.com) 正式版 手机 HUAWEI P60 HUAWEI P60 Pro HUAWEI P60 Art HUAWEI Mate X3 HUAWEI Mate X3 典藏版 HUAWEI Mate 50 HUAWEI Mate 50 Pro HUAWEI Mate 50 RS 保时捷设计 HUAWEI Mate 50E …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
