信息学奥赛一本通 1435:【例题3】曲线 | 洛谷 洛谷 P1883 函数
【题目链接】
ybt 1435:【例题3】曲线
洛谷 P1883 函数
【题目考点】
1. 三分
【解题思路】
每个 S i ( x ) S_i(x) Si(x)是一个二次函数, F ( x ) = m a x ( S i ( x ) ) F(x) = max(S_i(x)) F(x)=max(Si(x)),即为所有二次函数当自变量为x时的所有函数值的最大值。
已知 a ≥ 0 a \ge 0 a≥0,所以所有的二次函数都是开口向上的,为下凸函数。
首先要证明 F ( x ) F(x) F(x)在定义域为[0, 1000]的范围内是下凸函数(凸函数定义)
已知f(x),g(x)为下凸函数,证明h(x)=max(f(x),g(x))是一个下凸函数。
证明:
根据凸函数的定义,对于任意的 0 ≤ α ≤ 1 0\leq\alpha\leq1 0≤α≤1,定义域内的任意 x 1 , x 2 x1, x2 x1,x2,总有
f ( α x 1 + ( 1 − α ) x 2 ) ≤ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) ≤ α h ( x 1 ) + ( 1 − α ) h ( x 2 ) f(\alpha{x1}+(1-\alpha)x2)\leq\alpha{f(x1)}+(1-\alpha){f(x2)}\leq\alpha{h(x1)}+(1-\alpha){h(x2)} f(αx1+(1−α)x2)≤αf(x1)+(1−α)f(x2)≤αh(x1)+(1−α)h(x2)
同理,对于g(x)也有相似的结论:
g ( α x 1 + ( 1 − α ) x 2 ) ≤ α g ( x 1 ) + ( 1 − α ) g ( x 2 ) ≤ α h ( x 1 ) + ( 1 − α ) h ( x 2 ) g(\alpha{x1}+(1-\alpha)x2)\leq\alpha{g(x1)}+(1-\alpha){g(x2)}\leq\alpha{h(x1)}+(1-\alpha){h(x2)} g(αx1+(1−α)x2)≤αg(x1)+(1−α)g(x2)≤αh(x1)+(1−α)h(x2)将 x = α x 1 + ( 1 − α ) x 2 x=\alpha{x1}+(1-\alpha)x2 x=αx1+(1−α)x2带入 h ( x ) h(x) h(x),有
h ( α x 1 + ( 1 − α ) x 2 ) = m a x ( f ( α x 1 + ( 1 − α ) x 2 ) , g ( α x 1 + ( 1 − α ) x 2 ) ) ≤ m a x ( α h ( x 1 ) + ( 1 − α ) h ( x 2 ) , α h ( x 1 ) + ( 1 − α ) h ( x 2 ) ) = α h ( x 1 ) + ( 1 − α ) h ( x 2 ) h(\alpha{x1}+(1-\alpha)x2)=max(f(\alpha{x1}+(1-\alpha)x2),g(\alpha{x1}+(1-\alpha)x2))\leq max(\alpha{h(x1)}+(1-\alpha){h(x2)},\alpha{h(x1)}+(1-\alpha){h(x2)})= \alpha{h(x1)}+(1-\alpha){h(x2)} h(αx1+(1−α)x2)=max(f(αx1+(1−α)x2),g(αx1+(1−α)x2))≤max(αh(x1)+(1−α)h(x2),αh(x1)+(1−α)h(x2))=αh(x1)+(1−α)h(x2)
h(x)满足下凸函数的定义,因此也是下凸函数
已知f(x),g(x)两个函数的较大值h(x)=max(f(x),g(x))是下凸函数,那么多个函数的最大值 F ( x ) F(x) F(x)也是下凸函数。
已知 F ( x ) F(x) F(x)在定义域[0,1000]中是下凸函数(单谷函数),因此可以使用三分求单谷函数的极小值点。
首先把左端点l设为0,右端点r设为1000
每次循环取三分点lm = l+(r-l)/3, rm = r-(r-l)/3
求出两个三分点位置的函数值f(lm)、f(rm)
设极值点为m(注:极值点是取到极值时函数自变量的值)
- 当f(lm)<f(rm)时,可能是lm < m < rm,或m < lm < rm,极值点一定不在[rm, r]的范围内,因此使
r = rm,[l, r]的范围缩减1/3。 - 当f(lm)>f(rm)时,可能是lm < m < rm,或lm > rm > m,极值点一定不在[l, lm]的范围内,因此使
l = lm,[l, r]的范围缩减1/3。
当 r − l < 1 0 − 10 r-l < 10^{-10} r−l<10−10时,跳出循环,此时l或r都是极值点的近似值。
求极值点位置的函数值,即为 f ( l ) f(l) f(l)
三分算法的时间复杂度: O ( l o g n ) O(log n) O(logn),n为初始的数值范围大小,在本题中为1000。
【注】:r与l差值很小时结束循环,对于一般的结果保留几位小数的问题(比如保留5位,8位等),将差值取为 1 0 − 10 10^{-10} 10−10是合理的。取 r − l < 1 0 − 10 r-l<10^{-10} r−l<10−10与取 r − l < 1 0 − 5 r-l<10^{-5} r−l<10−5在循环次数上是相同数量级的,而且能保证结果的准确性。
【题解代码】
解法1:三分
#include<bits/stdc++.h>
using namespace std;
#define N 10005
int a[N], b[N], c[N], n, t;//a[i], b[i], c[i]:第i个二次函数的a、b、c
double f(double x)
{double ans = -1e9;for(int i = 1; i <= n; ++i)ans = max(ans, a[i]*x*x+b[i]*x+c[i]);return ans;
}
int main()
{scanf("%d", &t);while(t--){scanf("%d", &n);for(int i = 1; i <= n; ++i)scanf("%d%d%d", &a[i], &b[i], &c[i]);double l = 0, r = 1000;while(r-l >= 1e-10){double lm = l+(r-l)/3, rm = r-(r-l)/3;if(f(lm) > f(rm))l = lm;elser = rm;}printf("%.4f\n", f(l));}return 0;
}
相关文章:

信息学奥赛一本通 1435:【例题3】曲线 | 洛谷 洛谷 P1883 函数
【题目链接】 ybt 1435:【例题3】曲线 洛谷 P1883 函数 【题目考点】 1. 三分 【解题思路】 每个 S i ( x ) S_i(x) Si(x)是一个二次函数, F ( x ) m a x ( S i ( x ) ) F(x) max(S_i(x)) F(x)max(Si(x)),即为所有二次函数当自变量…...

OpenCV入门2——图像视频的加载与展示一些API
文章目录 题目OpenCV创建显示窗口OpenCV加载显示图片题目 OpenCV保存文件利用OpenCV从摄像头采集视频从多媒体文件中读取视频帧将视频数据录制成多媒体文件OpenCV控制鼠标关于[np.uint8](https://stackoverflow.com/questions/68387192/what-is-np-uint8) OpenCV中的TrackBar控…...

「校园 Pie」 系列活动正式启航,首站走进南方科技大学!
PieCloudDB 社区校园行系列活动「校园 Pie」已正式启动。「校园 Pie」旨在促进数据库领域的学术交流,提供一个平台让学生们了解最新的数据库发展趋势和相关技术应用。 在「校园 Pie」系列活动中,PieCloudDB 社区将携拓数派技术专家,社区大咖…...
【PyQt小知识 - 3】: QComboBox下拉框内容的设置和更新、默认值的设置、值和下标的获取
QComboBox 内容的设置和更新 from PyQt5.QtWidgets import * import sysapp QApplication(sys.argv)mainwindow QMainWindow() mainwindow.resize(200, 200) # 设置下拉框 comboBox QComboBox(mainwindow) comboBox.addItems([上, 中, 下])button QPushButton(更新, main…...

Oracle OCM考试(史上最详细的介绍,需要19c OCP的证书)
Oracle 19c OCM考试和之前版本的OCM考试差不多,对于考生来说最大的难点是题量大,每场3小时,一共4场,敲键盘敲得手抽筋。姚远老师(v:dataace)的很多Oracle OCP学员都对19c OCM考试很有兴趣,这里给…...

广州华锐互动VRAR:VR教学楼地震模拟体验增强学生防震减灾意识
在当今社会,地震作为一种自然灾害,给人们的生活带来了巨大的威胁。特别是在学校这样的集体场所,一旦发生地震,后果将不堪设想。因此,加强校园安全教育,提高师生的防震减灾意识和能力,已经成为了…...

?. 语法报错
报错 Syntax Error: SyntaxError: E:xxx\src\views\xxx.vue: Support for the experimental syntax ‘optionalChaining’ isn’t currently enabled (173:27): 171 | label: node.label, 172 | style: { 173 | fill: colorSet?.mainFill || ‘#DEE9FF’, | ^ 174 | stroke: …...
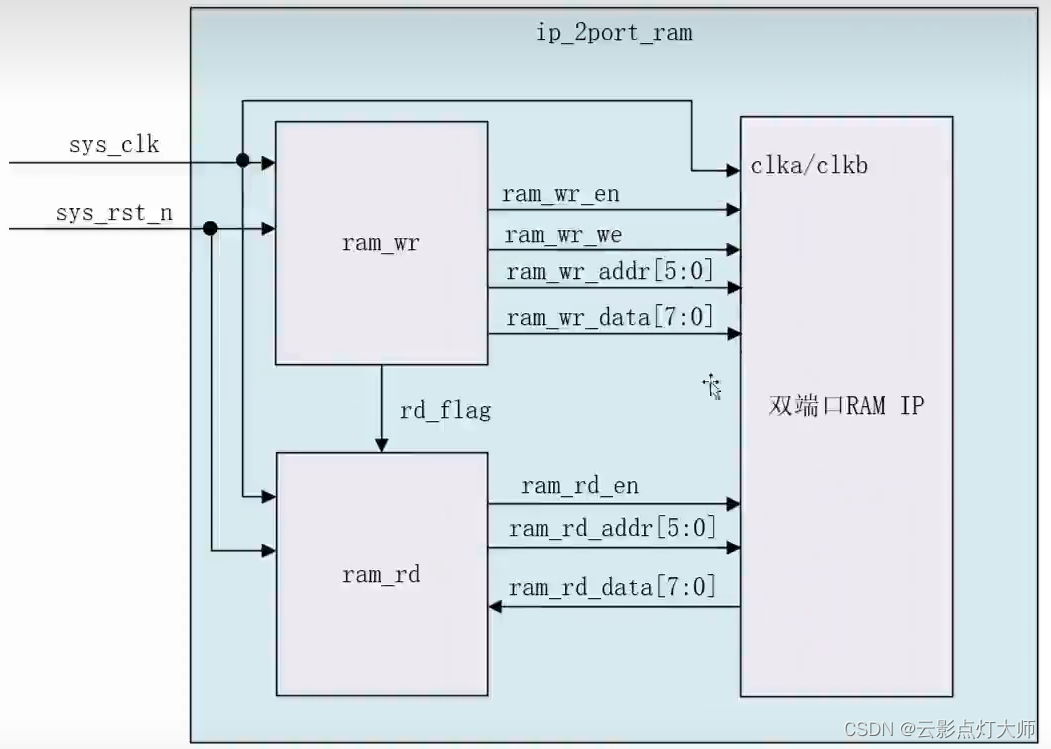
FPGA——IP核 基础操作
FPGA——IP核 基础操作 IP核例化模块时钟IP核RAM IP核 IP核例化模块 找到模版 加入代码中 时钟IP核 配置模式功能 配置输入时钟 输出配置 RAM IP核...

unity unityWebRequest 通过http下载服务器资源
直接下载不显示进度 private void OnDownloadAssets()//下载资源{StartCoroutine(DownloadFormServer_IE(url, savePath));}//其他方法private IEnumerator DownloadFormServer_IE(string url, string path)//从服务器下载资源{Debug.Log("正在下载" url);UnityWebR…...
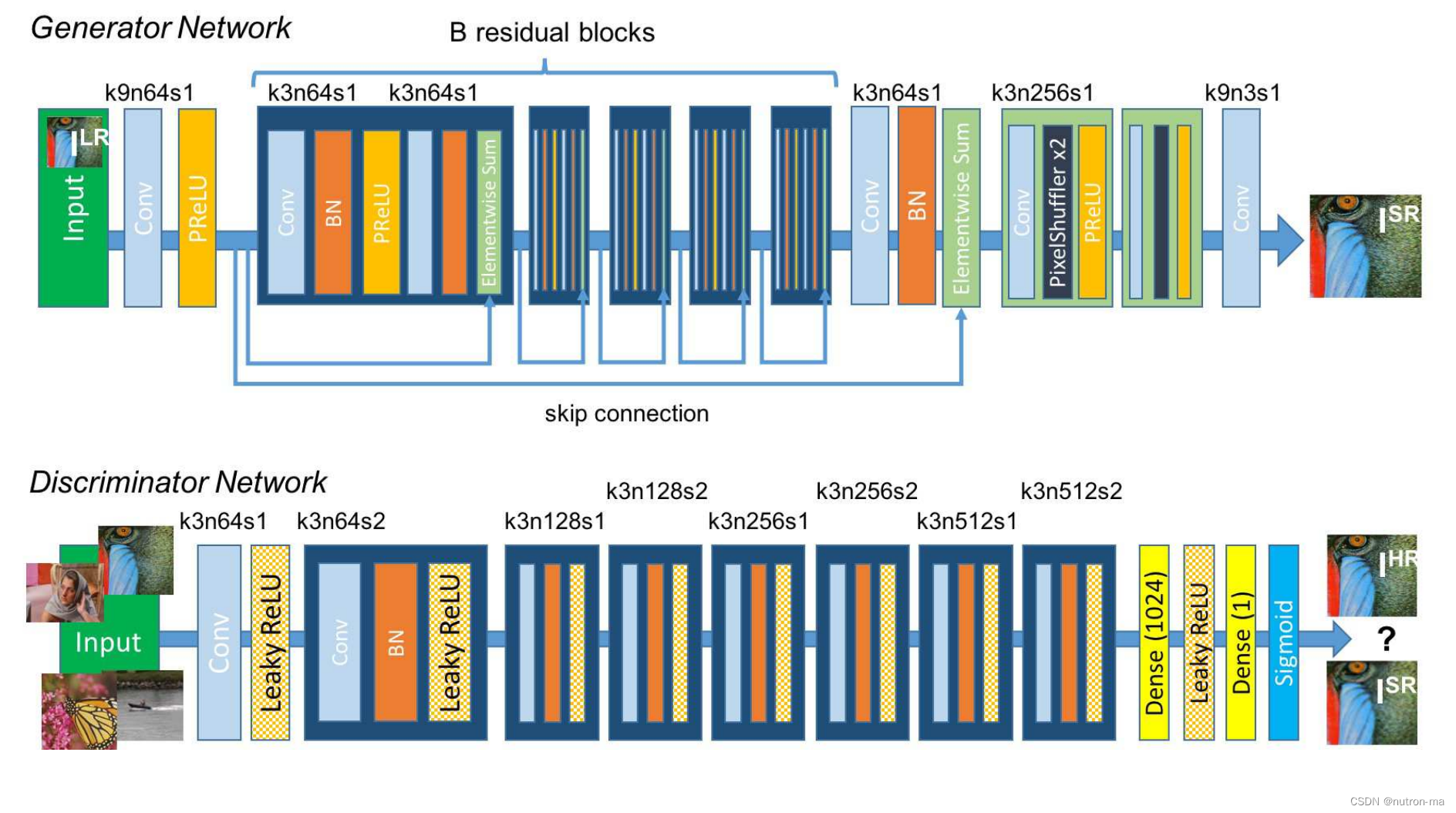
13-1-SRGAN-图像超分-残差模块-亚像素卷积
文章目录 1 定义生成器Generator残差模块生成器亚像素卷积2 定义判别器Discriminator3 训练1 判别器训练2 生成器训练3 程序细节使用use.py参考: 论文: https://arxiv.org/abs/1609.04802 论文翻译: https://blog.csdn.net/MR_kdcon/article/details/123525914 代码: SRG…...
Maya v2024(3D动画制作软件)
Maya 2024是一款三维计算机图形动画制作软件。它被广泛应用于电影、电视、游戏、动画等领域中,用于创建各种三维模型、场景、特效和动画。 以下是Maya的主要特点: 强大的建模工具:Maya提供了各种建模工具,如多边形建模、NURBS建模…...
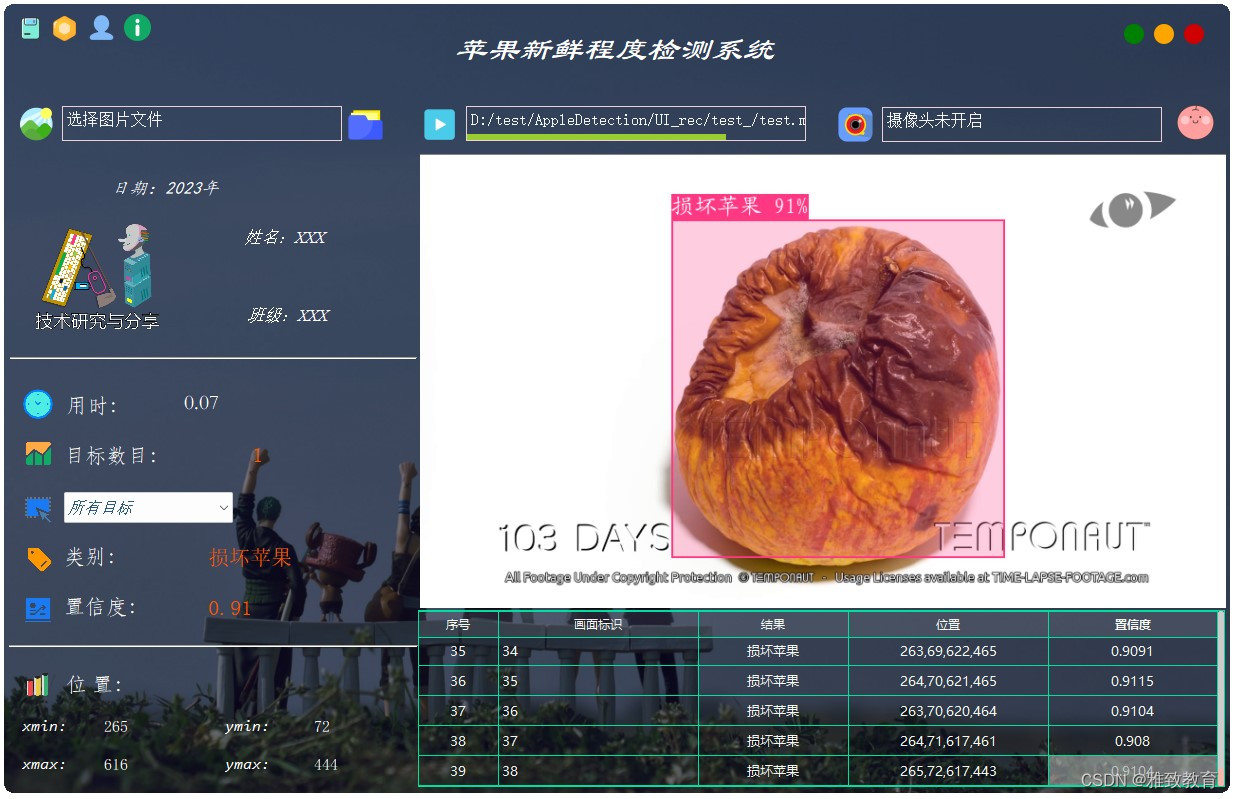
深度学习之基于YoloV5苹果新鲜程度检测识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 深度学习之基于 YOLOv5 苹果新鲜程度检测识别系统介绍YOLOv5 简介苹果新鲜程度检测系统系统架构应用场景 二、功能三、系统四. 总结 一项目简介 深度学习之…...

git 构建报错
钉钉插件]当前任务未配置机器人,已跳过 org.codehaus.groovy.control.MultipleCompilationErrorsException: startup failed: WorkflowScript: 4: Tool type “maven” does not have an install of “maven-3.8.8” configured - did you mean “Maven-3.8.8”? …...
【Linux专题】firewalld 过滤出接口流量
【赠送】IT技术视频教程,白拿不谢!思科、华为、红帽、数据库、云计算等等_厦门微思网络的博客-CSDN博客文章浏览阅读428次。风和日丽,小微给你送福利~如果你是小微的老粉,这里有一份粉丝福利待领取...如果你是新粉关注到了小微&am…...
)
ElasticSearch语句中must,must_not,should组合关系,作者有验证脚本(ES为8版本,使用Kibana运行语句)
文章目录 一、单个使用二、must和must_not组合(A-B)三、must和should组合(A)四、should和must_not组合(A-B)五、must和should和must_not组合(A-C)六、验证脚本,执行之后自…...
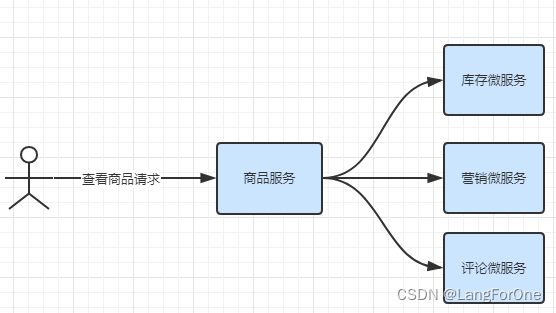
SpringCloud Alibaba组件入门全方面汇总(中):服务熔断降级-Sentinel
文章目录 Sentinel常见的容错思路Sentinel流量控制规则sentinel 自定义异常 sentinelresources 注解使用Feign整合Sentinel**面试题:结合Feign后,你在项目中的降级方法中会实现什么样的操作/功能?** Sentinel Sentinel是阿里巴巴开源的分布…...

算法通关村第十关|青铜|快速排序
快速排序的核心框架是“二叉树的前序遍历对撞型双指针”。 快速排序的实现1: public void quickSort(int[] arr, int left, int right) {if (left < right) {// pivot将遍历的范围限制在了pivot之前int pivot arr[right];int i left - 1;for (int j left; j…...
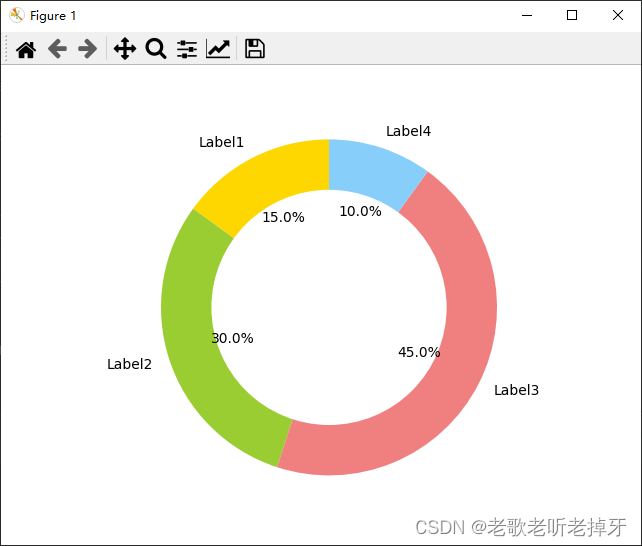
python科研绘图:圆环图
圆环图是一种特殊的图形,它可以显示各个部分与整体之间的关系。圆环图由两个或多个大小不一的饼图叠加而成,中间被挖空,看起来像一个甜甜圈。因此,圆环图也被称为“甜甜圈”图。 与饼图相比,圆环图的空间利用率更高&a…...
【Linux】C文件系统详解(一)——C文件操作
文章目录 文件操作总结预备知识结论: C文件操作回顾语言方案w写入方式a写入方式r只读方式 系统方案但是这个**没有设置权限**,需要这样改: 文件操作总结 1.文件描述符,重定向,缓冲区,语言和系统关于文件的不同的视角的理解 – 都是要让我们深刻理解文件 2.文件系统 3.动静态库 …...
uniapp 实现微信小程序手机号一键登录
app 和 h5 手机号一键登录,参考文档:uni-app官网 以下是uniapp 实现微信小程序手机号一键登录 1、布局 <template><view class"mainContent"><image class"closeImg" click"onCloseClick"src"quic…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
