2023年亚太杯数学建模思路 - 复盘:光照强度计算的优化模型
文章目录
- 0 赛题思路
- 1 问题要求
- 2 假设约定
- 3 符号约定
- 4 建立模型
- 5 模型求解
- 6 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 问题要求
现在已知一个教室长为15米,宽为12米,在距离地面高2.5米的位置均
匀的安放4个光源(分别为1、2、3、4),各个光源的光照强度均为一个单位,如下图
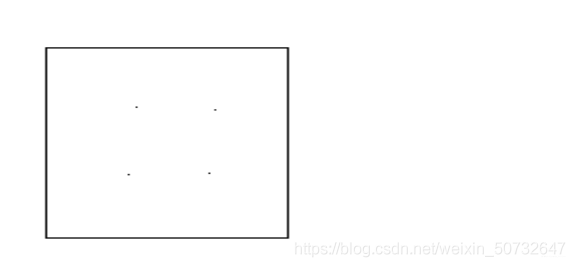
要求:
- (1)如何计算教室内任意一点的光照强度?(光源对目标点的光照强度与该光源到目标点距离的平方成反比,与该光源的强度成正比).
- (2)画出距离地面1米处各个点的光照强度与位置(横纵坐标)之间的函数关系曲面图,试同时给出一个近似的函数关系式.
- (3)假设离地面1米高正是学生桌面的高度,如何设计这四个点光源的位置,才能使学生对光照的平均满意度达到最高?
- (4)若将题目中的点光源换成线光源,以上(2)、(3)问的结果又如何?
(对于(1)、(2)问,假设横向(纵向)墙壁与光源、光源与光源、光源与墙壁之间的距离是相等的.)
2 假设约定
- 1 光不会通过窗、门等外涉,也不考虑光在空气中的消耗,即光照强度和不变;
- 2 室内不受外界光源影响;
- 3 教室高度为2.5米;
- 4 不考虑光的反射;
- 5 线光源发光是均匀的.
3 符号约定

4 建立模型
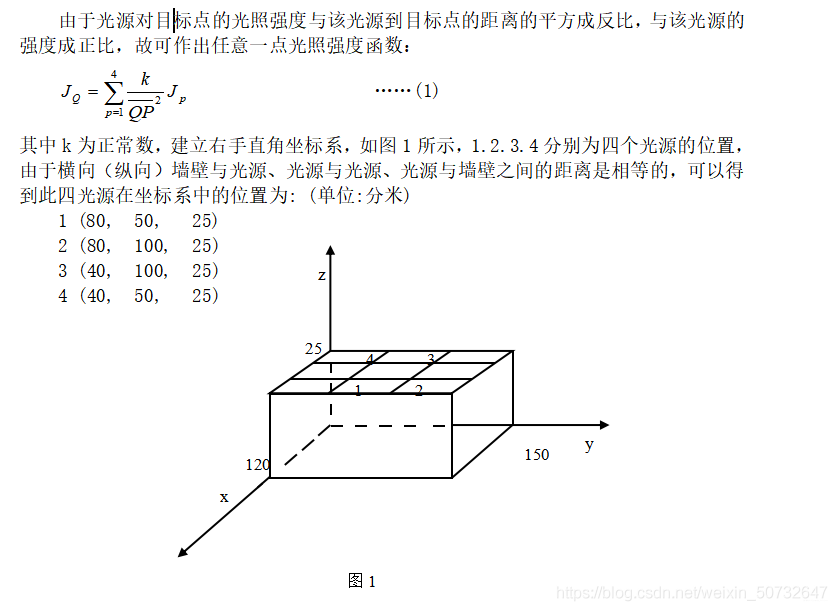

5 模型求解

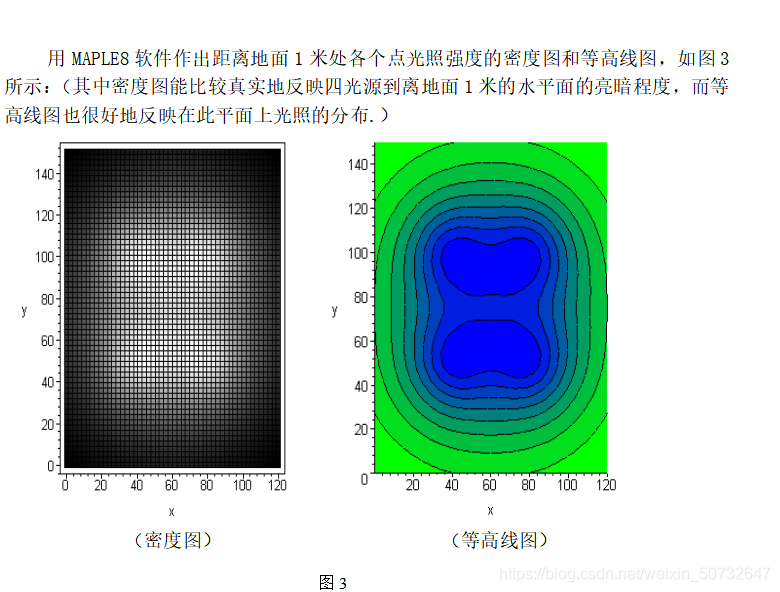
6 实现代码
matlab 实现代码
建议最好用python去实现,图会好看一些,而且国内当前趋势会逐渐淘汰matlab,目前有些学校已经无法使用matlab了
clear
clc
max=0;min=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));endendif l>maxmax=l;x11=x1;y11=y1;x12=x2;y12=y2;x13=x3;y13=y3;x14=x4;y14=y4;endp=l./(120.*150);Q=0;for x=0:0.1:12for y=0:0.1:15Q=Q+(k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2))-p).^2.^(1./2);endendif min>Qmin=Q;x21=x1;y21=y1;x22=x2;y22=y2;x23=x3;y23=y3;x24=x4;y24=y4;endend
end
disp(['最大值','x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
disp(['最平均','x21=',num2str(x21),' ','y21=',num2str(y21),' ','x22=',num2str(x22),' ','y22=',num2str(y22),' ','x23=',num2str(x23),' ','y23=',num2str(y23),' ','x24=',num2str(x24),' ','y24=',num2str(y24)])
附录二:
clear
clc
max=0;min=4;li=4;
for i=0:0.1:3for j=0.1:0.1:4s=0;x1=8+i,y1=5-jx2=8+i,y2=10+jx3=4-i,y3=10+jx4=4-i,y4=5-j for x=0:0.1:12for y=0:0.1:15for z=0:0.1:2.5if x1~=x & y1~=y & x2~=x & y2~=y & x3~=x & y3~=y & x4~=x & y4~=y s=s+1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1./((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2);endendendendk=4./s;l=0;z=1;e=0for x=0:0.1:12for y=0:0.1:15l=l+k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));r=k.*(1./((x1-x).^2+(y1-y).^2+(2.5-z).^2)+1/((x2-x).^2+(y2-y).^2+(2.5-z).^2)+1./((x3-x).^2+(y3-y).^2+(2.5-z).^2)+1./((x4-x).^2+(y4-y).^2+(2.5-z).^2));e=e+(r-6*10^(-32))^2;endendS=(l-0.1278)^2+eif S<lili=Sx11=x1,y11=y1, x12=x2,y12=y2, x13=x3,y13=y3, x14=x4,y14=y4,en4en4
en4
disp(['x11=',num2str(x11),' ','y11=',num2str(y11),' ','x12=',num2str(x12),' ','y12=',num2str(y12),' ','x13=',num2str(x13),' ','y13=',num2str(y13),' ','x14=',num2str(x14),' ','y14=',num2str(y14)])
li
建模资料
资料分享: 最强建模资料


相关文章:

2023年亚太杯数学建模思路 - 复盘:光照强度计算的优化模型
文章目录 0 赛题思路1 问题要求2 假设约定3 符号约定4 建立模型5 模型求解6 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 问题要求 现在已知一个教室长为15米,宽为12米&…...

Unity——利用Mesh绘制图形
什么是Mesh? Mesh 是用于表示和存储3D模型几何信息的类。它包含了顶点坐标、法线、UV坐标和其他与几何形状相关的数据,同时也包含了定义了这些数据如何连接以形成三角形的索引。 通过Mesh类,你可以创建、修改和渲染3D模型。一些常见的操作包括…...
web3资讯及远程工作
各位如果想了解区块链相关的消息可以通过如下网址了解,里面还会有相关职位招聘(包括远程工作),还可以在里面进行发帖,进入即可获得1000积分,后期可以兑换一些礼品Cryptosquare...
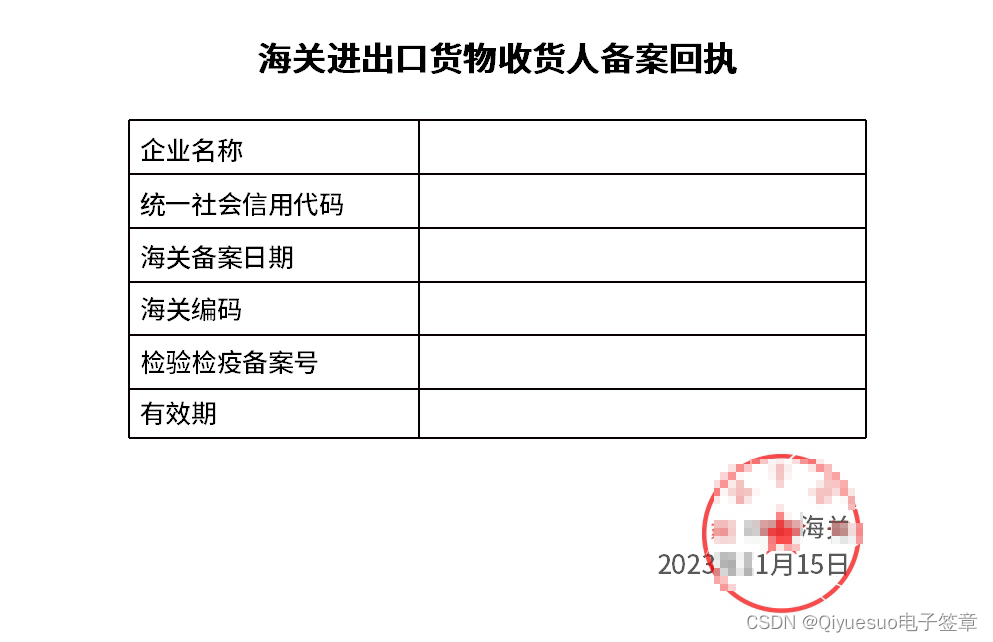
契约锁助力货物进出口全程无纸化,加速通关、降低贸易成本
我国作为全球最大的制造业国家和最大的货物贸易国家,政府始终注重引入数字化技术,创新管理和服务模式,帮助降低企业进出口成本,加速货物流通。 近年国家海关总署、商务部、税务总局及各地政府在进出口“报关”、“提货”、“收货备…...

生活中的综合能力
暖气管道不通 1 逐层排查哪层管道不通 2 排查该栋楼主管道和锅炉房总管道的连接口是否通畅 找不到主管道和总管道的连接口 查看其他楼和总管道的连接口 复盘: 先整体,后局部 求同求异思维:找差异,找正常暖气管道和异常暖气管…...
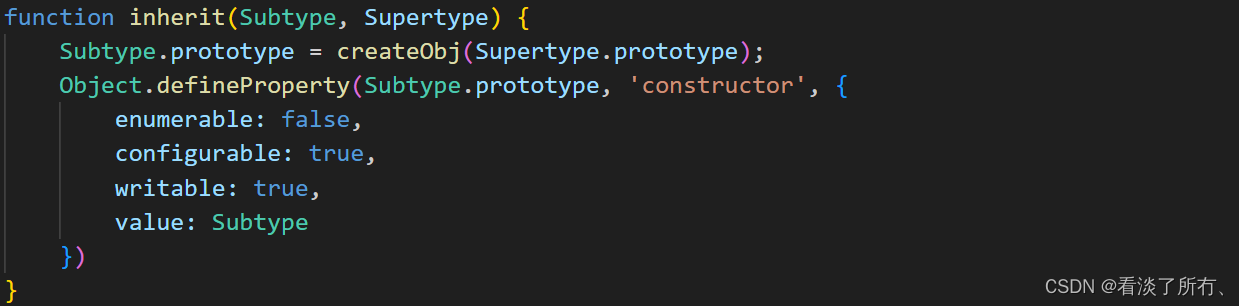
ES5中实现继承
本篇文章主要说明在ES5中最通用最兼容的继承实现方式,继承作为面向对象的三大特性之一,在js中实现继承对代码的简洁性,逻辑的连贯性都有很大的帮助。 实现思路 封装创建中间联系对象的函数 继承可以简单理解为建立子类和父类之间的联系&…...
面试鸭 - 专注于面试刷题的网站
网上面试题有很多,但此套面试题真实、原创、高频,全网最强。 题目涵盖大中小公司,真实靠谱,有频率和难度的标记,助你成为Offer收割机。 面试鸭地址:https://mianshiya.skyofit.com/ 本套题是我原创&…...

解决小程序路由超过10层限制
新建 navroter.js // 路由判断,小程序路由超过10层限制 // 避免小程序商品重复切换导致页面到结算单页时无法跳转到收货地址页,所以这里层级限制最大数为8 const MAX_VALUE 8 export function navigateTo(url) {let pages getCurrentPages()let dlt …...

【ceph】AI时代-数据为王-ceph存储将成为未来比较看好的赛道之一,为什么不all in一把学习一个不那么卷的赛道呢?
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...

《小·意·思》特殊符号
title: 《小意思》特殊符号 date: 2023-11-17 15:27:21 updated: 2023-11-17 15:27:21 categories: 小意思 excerpt: 上下标号、标点、运算符、标号、时间相关、语言、货币、音乐、形状符号、其他符号。 comments: false tags: top_image: /images/backimg/SunsetClimbing.png …...

Web server failed to start. Port 8080 was already in use.
Windows 服务端口被占用,杀死进程命令: netstat -ano | findstr 8080taskkill -PID [xxx] -F...

蓝桥杯第三周算法竞赛D题E题
发现更多计算机知识,欢迎访问Cr不是铬的个人网站 D迷宫逃脱 拿到题目一眼应该就能看出是可以用动态规划来解决。但是怎么定义dp呢? 这个题增加难度的点就在当所在位置与下一个要去的位置互质的时候,会消耗一把钥匙。当没有钥匙的时候就不能移动了。想…...

国家大基金三期线上金融正式倒计时!11月17日,共启芯片产业新篇章
国家大基金三期线上金融正式倒计时!11月17日,共启芯片产业新篇章 新时代浪潮下,全球化进程不断推动各科技大国的核心发展,芯片作为强有力的竞争标志,是国与国之间的重要技术战争焦点。同时,国内基金发展势…...

Chrony让内网设备时间同步
Centos 搭建NTP服务器 背景:公司服务器时间不同步导致一些认证功能无法使用,网络设备时间不同步日志信息不准确,因此想要在内网搭建一个NTP服务器,作为客户端同步网络时间服务器,作为服务端为内网其他终端提供授时服务…...
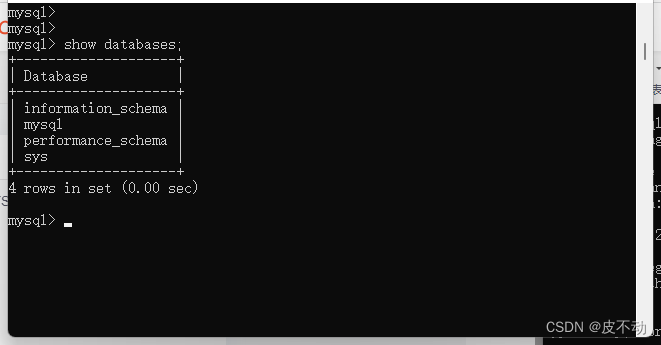
在docker中部署MySQL
目录 1、拉取最新的镜像 2、创建mysql容器实例 3、启动mysql实例 4、进入mysql 交互环境 5、登录MySQL数据库 6、尽情享用mysql 1、拉取最新的镜像 docker image pull mysql 2、创建mysql容器实例 第一次执行,需要先创建容器并启动(容器名是mys…...

百家网约车平台发布“阳光五条” 多举措加强司机保障
11月17日,免佣联盟百家网约车平台发布“阳光五条”,通过加大免佣力度、实行车费保镖司机版、72小时保护期等措施,加强对网约车司机的权益保障。 近年,交通运输部推动交通运输新业态平台企业落实“阳光行动”等工作,加…...

JXLS 导出多sheet,带页眉页脚
/*** 生成多sheet Excel* 带自定义页眉页脚** param templatePath* param sheetList* return* throws IOException*/public static byte[] generateMultiSheet(String templatePath, List<JxlsHelper2.SheetContext> sheetList) throws IOException {ByteArrayOutputStre…...
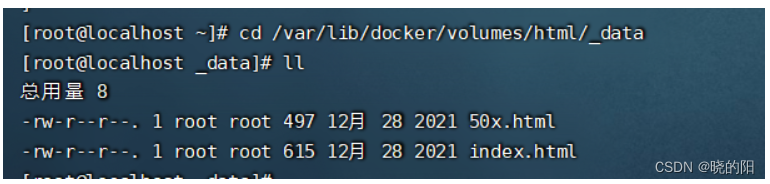
docker数据卷详细讲解及数据卷常用命令
docker数据卷详细讲解及数据卷常用命令 Docker 数据卷是一种将宿主机的目录或文件直接映射到容器中的特殊目录,用于实现数据的持久化和共享。Docker 数据卷有以下特点: 数据卷可以在一个或多个容器之间共享和重用,不受容器的生命周期影响。…...

智能井盖传感器能不能监测井盖位移
智能井盖传感器能够精准监测井盖的位移。这些传感器运用了前沿科技对井盖状态进行实时监测。一旦井盖出现异常移动传感器会立即捕捉到信号,并通过与互联网相连接的智能系统发出警报或记录数据。这种智能监测仪为城市或相关部门的井盖管理提供了实时数据支持…...

.bashrc文件中环境变量配置错误,导致linux命令无法正常使用
问题描述 配置环境变量时出错,导致linux命令无法使用 解决方案: 执行下面命令 export PATH/bin:/usr/local/sbin:/usr/local/bin:/sbin:/bin:/usr/sbin:/usr/bin vim就可以使用了,将错误纠正 vim ~/.bashrc 环境生效 source ~/.bashrc…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
