spark性能调优 | 默认并行度
Spark Sql默认并行度
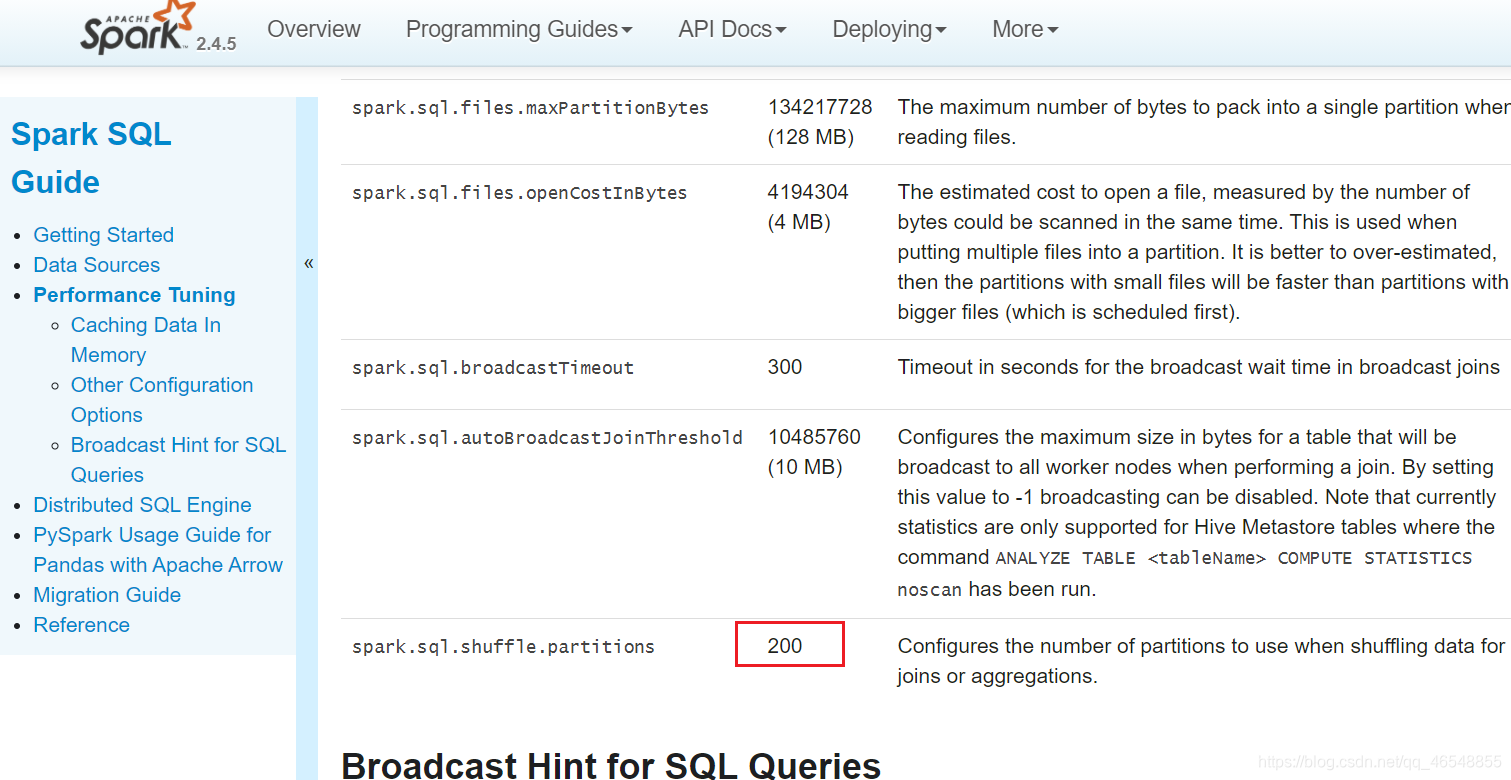
看官网,默认并行度200
https://spark.apache.org/docs/2.4.5/sql-performance-tuning.html#other-configuration-options

优化
在数仓中 task最好是cpu的两倍或者3倍(最好是倍数,不要使基数)
拓展
在本地 task需要自己设置,cpu就是local[x] x就代表cpu数
在yarn --num-executors 2 --executor-cores 2相乘就代表你的cpu个数
根据提交命令
spark-submit \
--master yarn \
--deploy-mode client \
--driver-memory 1g \
--num-executors 2 \
--executor-cores 2 \
--executor-memory 2g \
--queue spark \
--class com.donglin.sparksqltuning.PartitionTuning spark-sql-tuning-1.0-SNAPSHOT-jar-with-dependencies.jar
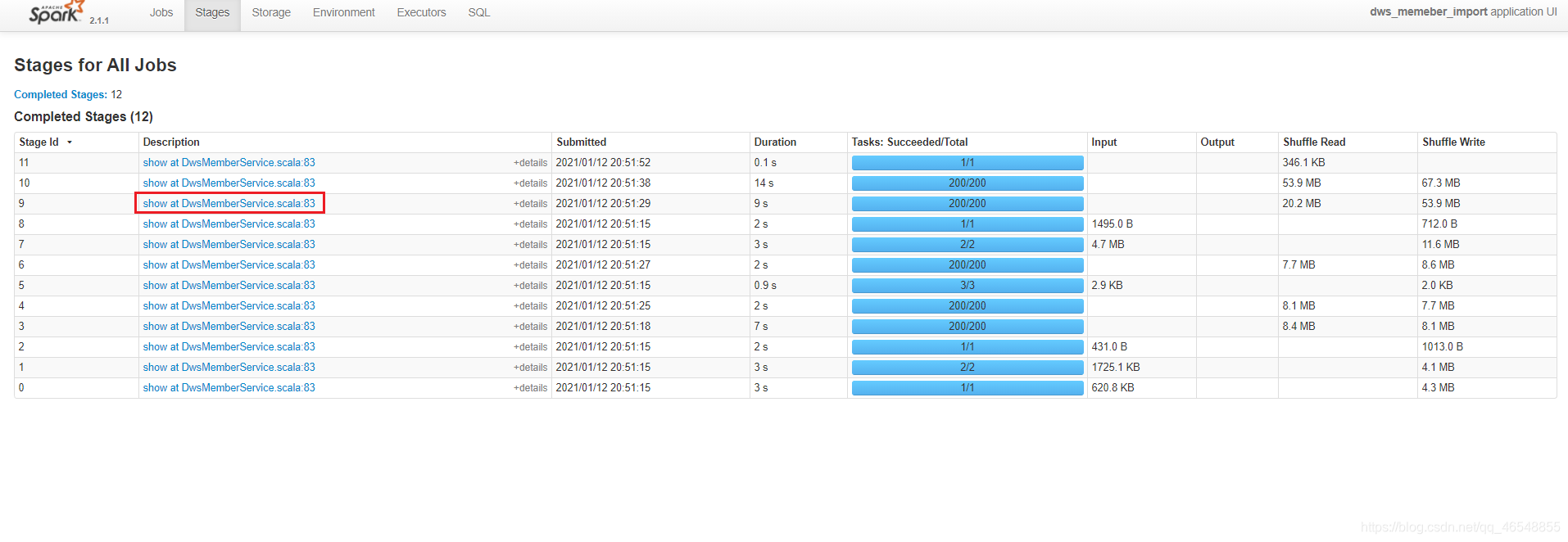
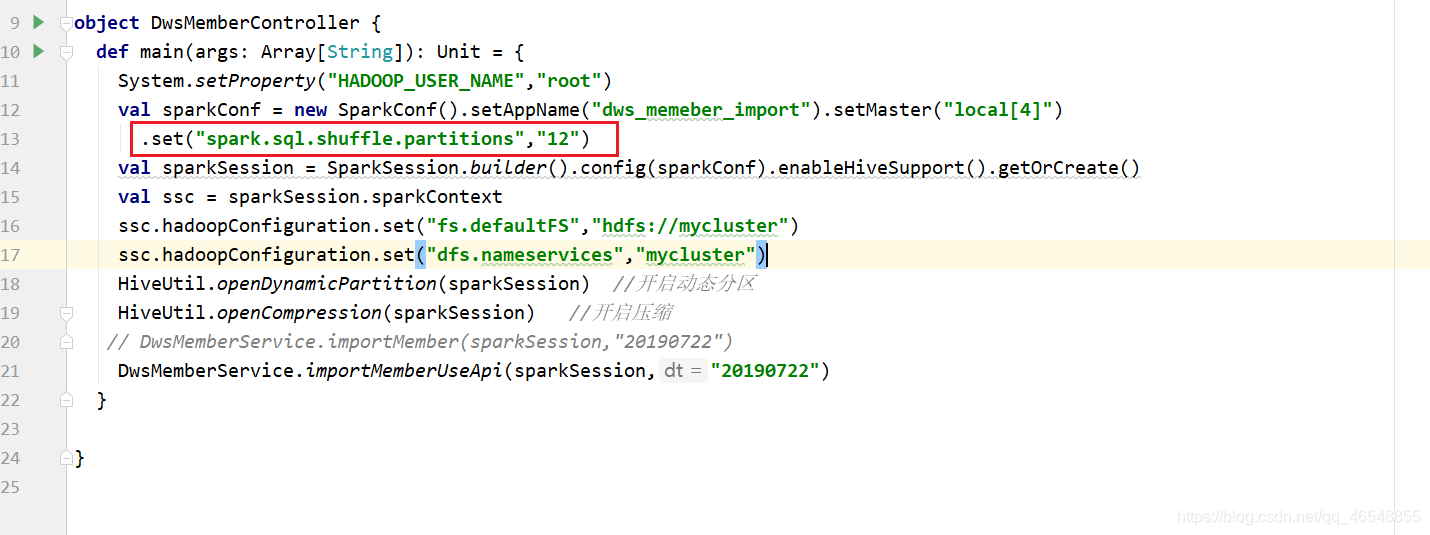
去向yarn申请的executor vcore资源个数为4个(num-executors*executor-cores),如果不修改spark sql分区个数,那么就会像上图所展示存在cpu空转的情况。这个时候需要合理控制shuffle分区个数。如果想要让任务运行的最快当然是一个task对应一个vcore,但是数仓一般不会这样设置,为了合理利用资源,一般会将分区(也就是task)设置成vcore的2倍到3倍。
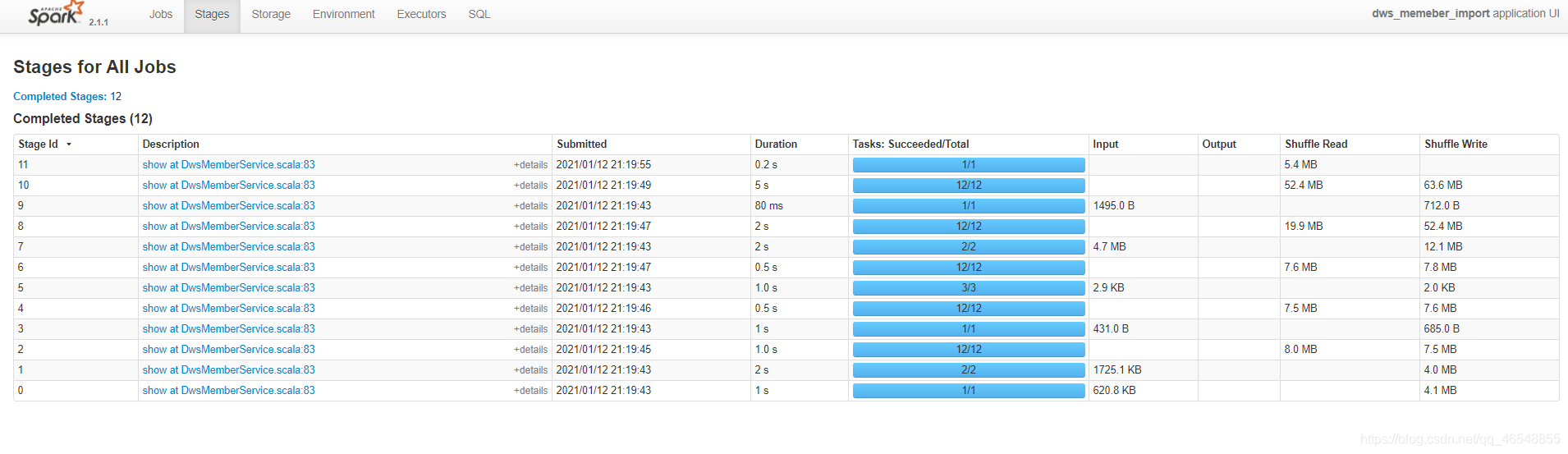
可以看出,时间快了不少!(这个需要多次调试,找出最优)
相关文章:

spark性能调优 | 默认并行度
Spark Sql默认并行度 看官网,默认并行度200 https://spark.apache.org/docs/2.4.5/sql-performance-tuning.html#other-configuration-options 优化 在数仓中 task最好是cpu的两倍或者3倍(最好是倍数,不要使基数) 拓展 在本地 task需要自己设置&a…...
Python-pptx教程之二操作已有PPT模板文件
文章目录 简单的案例找到要修改的元素修改幻灯片中的文本代码使用示例 修改幻灯片的图片代码使用示例 删除幻灯片代码使用示例 获取PPT中所有的文本内容获取PPT中所有的图片总结 在上一篇中我们已经学会了如何从零开始生成PPT文件,从零开始生成较为复杂的PPT是非常消…...

生活总是自己的,请尽情打扮,尽情可爱,,
同色系拼接羽绒服了解一下 穿上时尚感一下子就突显出来了 90白鸭绒填充,不仅时尚还保暖 设计感满满的羽绒服不考虑一下吗?...
栈和队列的初始化,插入,删除,销毁。
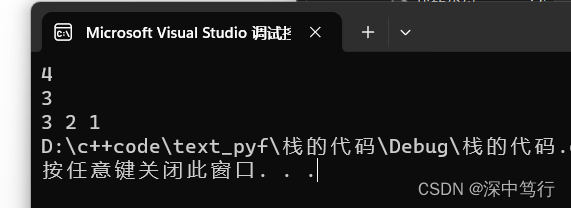
目录 题外话 顺序表和链表优缺点以及特点 一.栈的特点 二. 栈的操作 2.1初始化 2.2 栈的销毁 2.3 栈的插入 2.3 输出top 2.4 栈的删除 2.5 输出栈 题外话 顺序表和链表优缺点以及特点 特点:顺序表,逻辑地址物理地址。可以任意访问,…...

重温《Unix设计哲学》
重温Unix设计哲学 这个世界是复杂的,但往往本质的东西都是简单的。这些原则,不光是用在程序开发,也适用于架构设计,产品设计等等地方。 简洁原则:以简洁为美 不要为了满足自己的虚荣心,企图搞一些花哨的东…...
AIGC创作系统ChatGPT源码,AI绘画源码,支持最新GPT-4-Turbo模型,支持DALL-E3文生图
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...

Spring条件注解@Conditoinal+ Profile环境切换应用@Profile
Spring条件注解 一、创建一个maven项目 <dependencies><dependency><groupId>org.springframework</groupId><artifactId>spring-context</artifactId><version>5.1.5.RELEASE</version></dependency> </dependenc…...

Scrum框架中的Sprint
上图就是sprint里要做的事。Sprint是scrum框架的核心,是所有的想法、主意转换为价值的地方。所有实现产品目标的必要工作都在sprint里完成,这些工作主要包括Sprint 计划(Sprint planning)、每日站会(Daily Scrum&#…...

openfeign、nacos获取接口提供方真实IP
源码分析 client 是 LoadBalancerFeignClient org.springframework.cloud.openfeign.ribbon.LoadBalancerFeignClient#execute public Response execute(Request request, Request.Options options) throws IOException {try {URI asUri URI.create(request.url());String c…...
Linux系统编程学习 NO.9——git、gdb
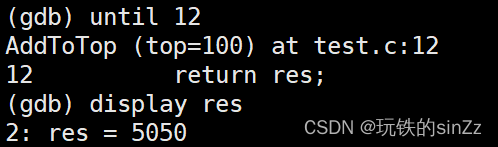
前言 本篇文章简单介绍了Linux操作系统中两个实用的开发工具git版本控制器和gdb调试器。 git 什么是git? git是一款开源的分布式版本控制软件。它不仅具有网络功能,还是服务端与客户端一体的软件。它可以高效的处理程序项目中的版本管理。它是Linux内…...

【联邦学习+区块链】TORR: A Lightweight Blockchain for Decentralized Federated Learning
文章目录 I.CONTRIBUTIONII. ASSUMPTIONS AND THREAT MODELA. AssumptionsB. Threat Model III. SYSTEM DESIGNA. Design OverviewB. Block DesignC. InitializationD. Role SelectionE. Storage ProtocolF. Aggregation ProtocolG. Proof of ReliabilityH. Blockchain Consens…...

《网络协议》08. 概念补充
title: 《网络协议》08. 概念补充 date: 2022-10-06 18:33:04 updated: 2023-11-17 10:35:52 categories: 学习记录:网络协议 excerpt: 代理、VPN、CDN、网络爬虫、无线网络、缓存、Cookie & Session、RESTful。 comments: false tags: top_image: /images/back…...

利用NVIDIA DALI读取视频帧
1. NVIDIA DALI简介 NVIDIA DALI全称是NVIDIA Data Loading Library,是一个用GPU加速的数据加载和预处理库,可用于图像、视频和语音数据的加载和处理,从而为深度学习的训练和推理加速。 NVIDIA DALI库的出发点是,深度学习应用中…...

TSINGSEE青犀AI智能分析+视频监控工业园区周界安全防范方案
一、背景需求分析 在工业产业园、化工园或生产制造园区中,周界防范意义重大,对园区的安全起到重要的作用。常规的安防方式是采用人员巡查,人力投入成本大而且效率低。周界一旦被破坏或入侵,会影响园区人员和资产安全,…...
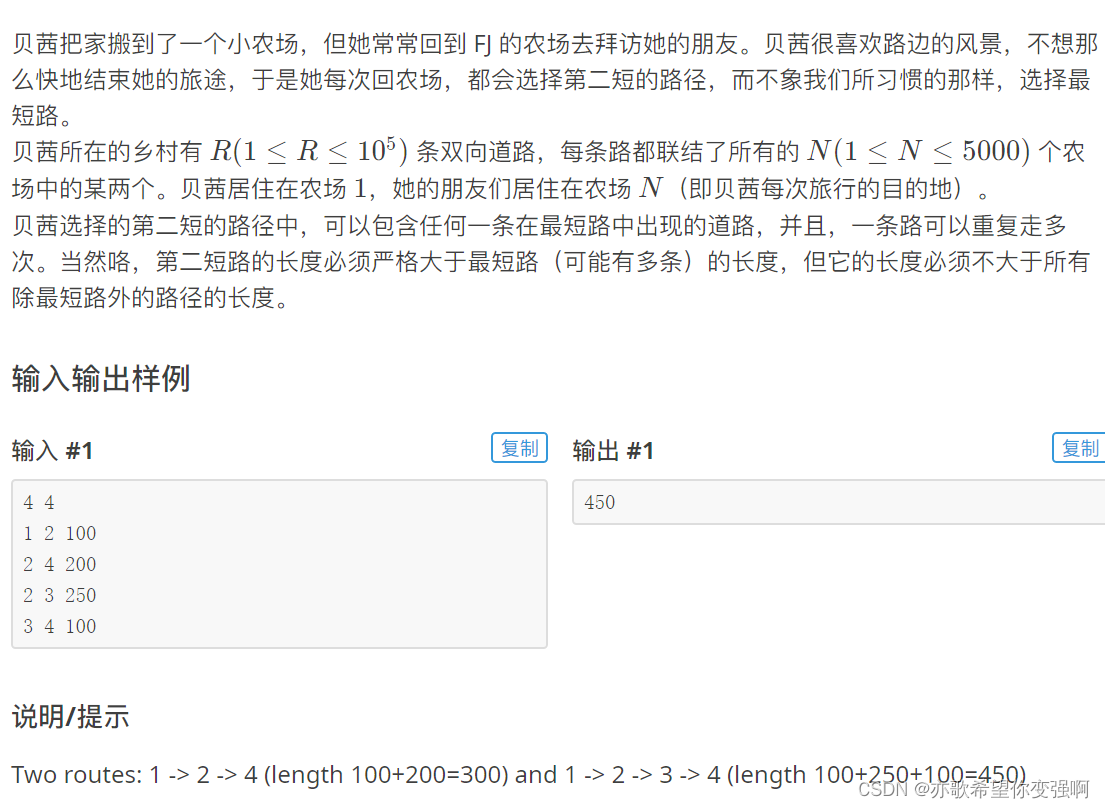
【算法每日一练]-图论(保姆级教程 篇5(LCA,最短路,分层图)) #LCA #最短路计数 #社交网络 #飞行路线 # 第二短路
今天讲最短路统计和分层图 目录 题目:LCA 思路: 题目:最短路计数 思路: 题目:社交网络 思路: 题目:飞行路线 思路: 题目:第二短路 思路: 题目&a…...
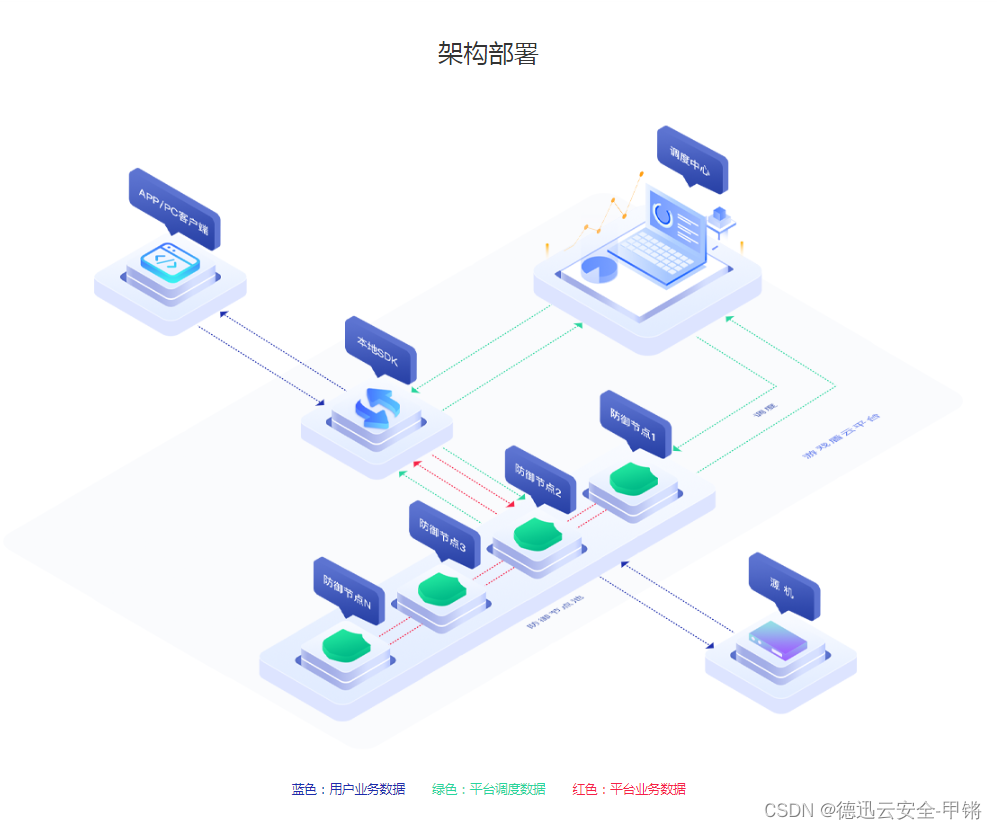
德迅云安全为您介绍关于抗D盾的一些事
抗D盾概述: 抗D盾是新一代的智能分布式云接入系统,接入节点采用多机房集群部署模式,隐藏真实服务器IP,类似于网站CDN的节点接入,但是“抗D盾”是比CDN应用范围更广的接入方式,适合任何TCP 端类应用包括&am…...
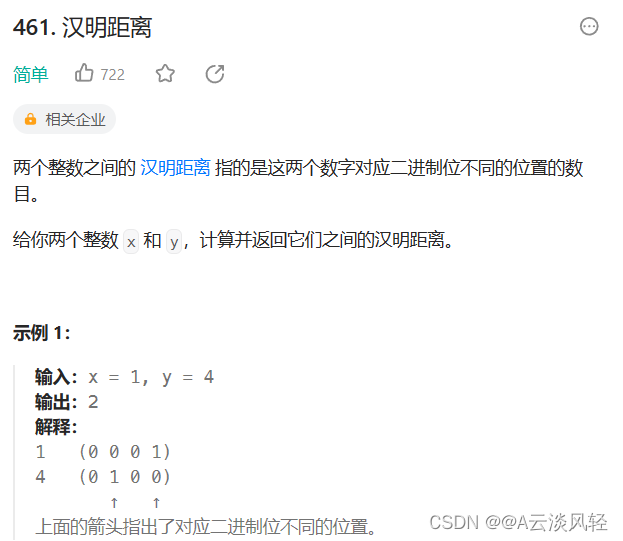
leetcode算法之位运算
目录 1.判断字符是否唯一2.丢失的数字3.两整数之和4.只出现一次的数字II5.消失的两个数字6.位1的个数7.比特位计数8.汉明距离 1.判断字符是否唯一 判断字符是否唯一 class Solution { public:bool isUnique(string astr) {//利用鸽巢原理做优化if(astr.size()>26) return…...
java常用的几个图片处理工具对Tiff文件的支持
ImageMagick 官网 https://imagemagick.org/, 支持多种格式。命令行工具很适合调试。功能很强大. 还有一款工具GraphicsMagick 是从ImageMagick的基础上研发出来的。 OpenCV 官网 https://opencv.org/ , github地址https://github.com/opencv/opencv&…...
-SQL查询篇(11)-联结表)
SQL必知会(二)-SQL查询篇(11)-联结表
第12课、联结表 联结表 使用联结:之前的 SELECT 查询某些列,只是针对一张表进行检索的。(即 FROM 表名)。但是如果用户想要使用 SELECT 对存储在不同表中的某些列时,则需要使用联结表的方式来实现。 例子中有建立两个…...

多模态大一统:开启全模态LLM和通用AI时代的大门
多模态大一统:开启全模态LLM和通用AI时代的大门 1. 目前多模态实现的方法1.1 单独训练各领域模型1.2 多任务学习1.3 集成多模态模型1.4 通用多模态模型2. 多模态统一难点2.1 数据集对齐和融合2.2 大规模计算资源需求2.3 各领域特性的兼容性2.4 可解释性和泛化能力3. 全模态的好…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
