R语言的入门学习
目录
- 准备工作
- 导入csv数据集
- 选择前200行作为数据集
- 展示数据集的前/后几N行
- 宏观分析
- 删除缺失值
- 构建直方图
- 导出为图片
- R语言常见图像类型
- 例1:散点图
- 例2:散点矩阵图
准备工作
- 安装教程: R语言和RStudio的下载安装(非常简便舒适)
导入csv数据集
- 右上角导入数据集。


选择前200行作为数据集
data <- BOOK_TEST[1:200,c(1,2,3)]
展示数据集的前/后几N行
head(data)
tail(data,10)

宏观分析
summary(data)

删除缺失值
- 这个测试数据集中并没有缺失值。
data = na.omit(data)
构建直方图
- 第三列数据是对书籍的打分。
hist(data$V3)

导出为图片

R语言常见图像类型
- 散点图(Scatter plot)、折线图(Line plot)、条形图(Bar plot)、直方图(Histogram)、箱线图(Box plot)、饼图(Pie chart)、热力图(Heatmap)、散点矩阵图(Scatterplot matrix)
例1:散点图
# 创建示例数据
x <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 6, 8, 10)# 创建散点图
plot(x, y, main = "Scatter Plot", xlab = "X", ylab = "Y", pch = 16, col = "blue")

例2:散点矩阵图
- 散点矩阵图(Scatterplot Matrix)是一种用于可视化多个变量之间关系的图表。它展示了数据集中多个变量两两之间的散点图,每个格子代表了两个变量之间的关系。散点矩阵图可以帮助我们观察和理解变量之间的相关性、分布情况以及可能存在的模式。
- 散点矩阵图的主要作用和使用场景如下:
- 变量关系探索:散点矩阵图可以帮助我们直观地观察多个变量之间的关系,特别是在变量较多时。通过观察散点图的分布和趋势,我们可以发现变量之间的线性或非线性关系,以及可能存在的异常值或离群点。
- 相关性分析:散点矩阵图可以帮助我们评估变量之间的相关性。通过观察散点图中点的分布情况,我们可以判断变量之间的相关性强弱、正负相关以及可能存在的非线性关系。
- 变量选择:散点矩阵图可以帮助我们在多个变量中选择与目标变量相关性较高的变量。通过观察散点图中与目标变量相关性较强的变量,我们可以选择最具有预测能力的变量进行进一步分析。
- 数据预处理:散点矩阵图可以帮助我们发现数据中的异常值、缺失值或其他数据质量问题。通过观察散点图中的异常点或缺失值模式,我们可以进行相应的数据清洗和预处理操作。
总之,散点矩阵图是一种强大的数据可视化工具,适用于探索性数据分析、相关性分析和变量选择等场景。它可以帮助我们更好地理解数据集中多个变量之间的关系,从而支持数据分析和决策过程。
# 创建示例数据
data <- iris[, 1:4]# 创建散点矩阵图
pairs(data, main = "Scatterplot Matrix")

相关文章:

R语言的入门学习
目录 准备工作导入csv数据集选择前200行作为数据集展示数据集的前/后几N行宏观分析删除缺失值构建直方图导出为图片 R语言常见图像类型例1:散点图例2:散点矩阵图 准备工作 安装教程: R语言和RStudio的下载安装(非常简便舒适&…...

【开源】基于Vue和SpringBoot的民宿预定管理系统
项目编号: S 058 ,文末获取源码。 \color{red}{项目编号:S058,文末获取源码。} 项目编号:S058,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 用例设计2.2 功能设计2.2.1 租客角色…...

nacos集群部署
GitHub - nacos-group/nacos-k8s: This project contains a Nacos Docker image meant to facilitate the deployment of Nacos on Kubernetes using StatefulSets. 需要修改两个文件 --- apiVersion: v1 kind: Service metadata:name: nacos-headlessnamespace: project-guli…...

9、传统计算机视觉 —— 边缘检测
本节介绍一种利用传统计算机视觉方法来实现图片边缘检测的方法。 什么是边缘检测? 边缘检测是通过一些算法来识别图像中物体之间,或者物体与背景之间的边界,也就是边缘。 边缘通常是图像中灰度变化显著的地方,标志着不同区域的分界线。 在一张图像中,边缘可以是物体的…...
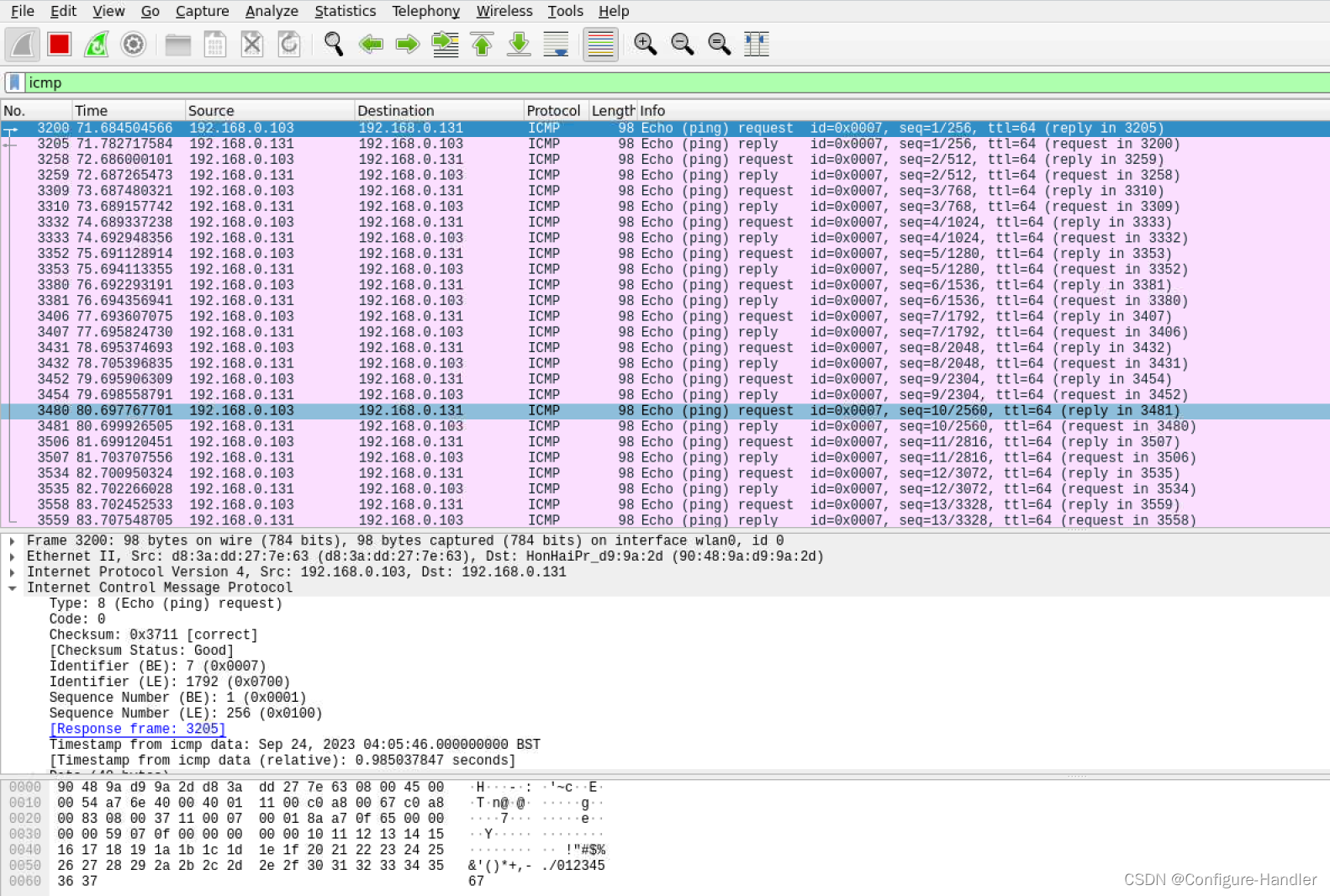
Linux tc 使用
tc模拟延时丢包等网络故障依赖的内核驱动 /lib/modules/5.15.0-52-generic/kernel/net/sched/sch_netem.ko有些系统并不是默认就安装上该驱动的,如果没有安装该驱动,构造网络故障时会报错。 root:curtis# tc qdisc change dev enp4s0 root netem delay…...

从0开始学习JavaScript--JavaScript 数字与日期
JavaScript中的数字和日期是处理数值计算和时间相关任务的核心。本文将深入研究JavaScript中数字的表示、常见运算,以及日期对象的创建、格式化等操作,并通过丰富的示例代码,可以更全面地了解和应用这些概念。 JavaScript数字基础 JavaScri…...

从关键新闻和最新技术看AI行业发展(2023.11.6-11.19第十期) |【WeThinkIn老实人报】
Rocky Ding 公众号:WeThinkIn 写在前面 【WeThinkIn老实人报】旨在整理&挖掘AI行业的关键新闻和最新技术,同时Rocky会对这些关键信息进行解读,力求让读者们能从容跟随AI科技潮流。也欢迎大家提出宝贵的优化建议,一起交流学习&…...
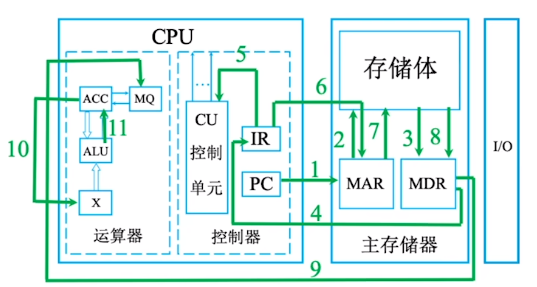
计算机硬件的基本组成
一、冯诺依曼结构 存储程序: “存储程序”的概念是指将指令以二进制代码的形式事先输入计算机的主存储器,然后按其在存储器中的首地址执行程序的第一条指令,以后就按该程序的规定顺序执行其他指令,直至程序执行结束。 冯诺依曼计…...

【算法-哈希表3】四数相加2 和 赎金信
今天,带来哈希表相关算法的讲解。文中不足错漏之处望请斧正! 理论基础点这里 1. 四数相加2 分析题意 求符合条件的四元组的出现次数,条件: nums1nums2nums3nums4 从四个数组中的每一个数组取一个数 num1, num2, num3, num4&am…...
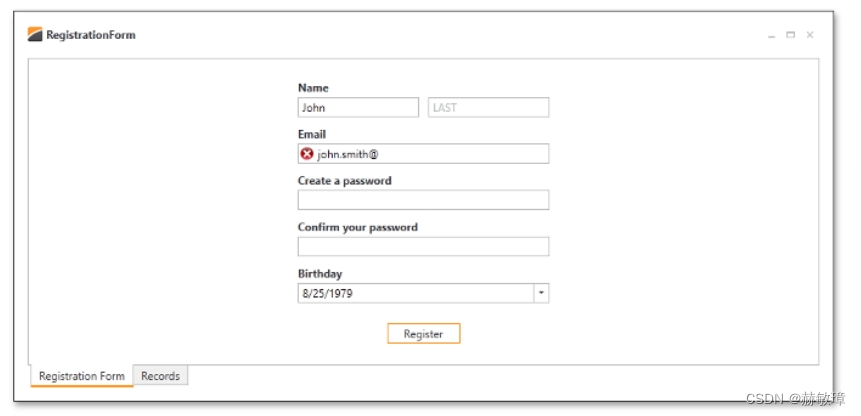
wpf devexpress自定义编辑器
打开前一个例子 步骤1-自定义FirstName和LastName编辑器字段 如果运行程序,会通知编辑器是空。对于例子,这两个未命名编辑器在第一个LayoutItem(Name)。和最终用户有一个访客左右编辑器查阅到First Name和Last Name字段,分别。如果你看到Go…...
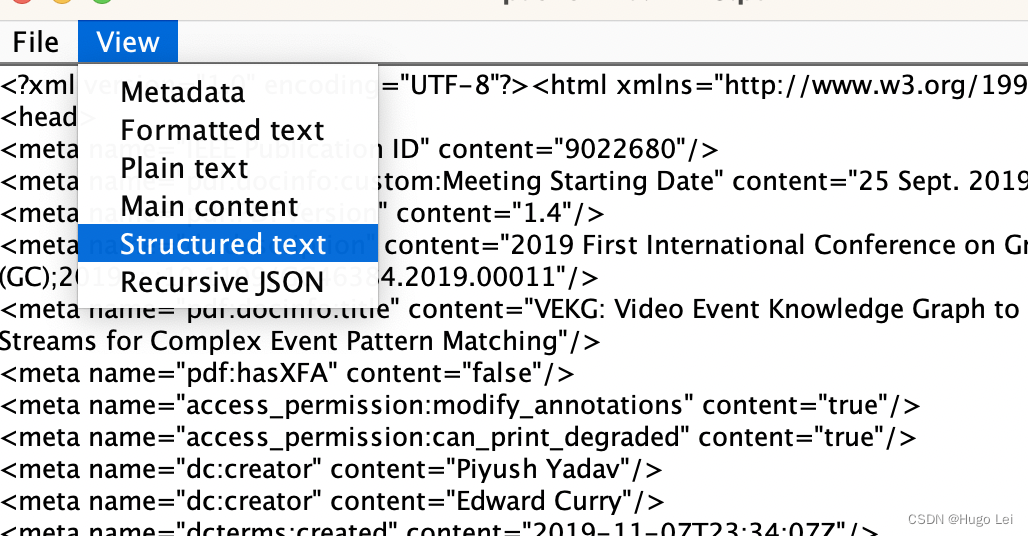
文档向量化工具(一):Apache Tika介绍
Apache Tika是什么?能干什么? Apache Tika是一个内容分析工具包。 该工具包可以从一千多种不同的文件类型(如PPT、XLS和PDF)中检测并提取元数据和文本。 所有这些文件类型都可以通过同一个接口进行解析,这使得Tika在…...

学习c#的第二十一天
目录 C# 泛型(Generic) 泛型类型参数 类型参数的约束 约束多个参数 未绑定的类型参数 类型参数作为约束 notnull 约束 class 约束 default 约束 非托管约束 委托约束 枚举约束 类型参数实现声明的接口 泛型类 泛型方法 泛型和数组 泛型…...

Michael Jordan最新报告:去中心化机器学习中的契约、不确定性和激励
导读 11月3日,智源研究院学术顾问委员会委员、机器学习泰斗Michael Jordan在以“新一代人工智能前沿”为主题的2023北京论坛 新工科专题论坛上,发表了题为Contracts, Uncertainty, and Incentives in Decentralized Machine Learning(去…...

3ds Max渲染用专业显卡还是游戏显卡?
使用3dsmax建模时,会面临诸多选择,除了用vr还是cr的决策,硬件选择上也存在着疑问,比如用专业显卡还是消费级游戏显卡?一般来说,除非是特别专业的大型项目和软件,且预算在5位数以上,常…...
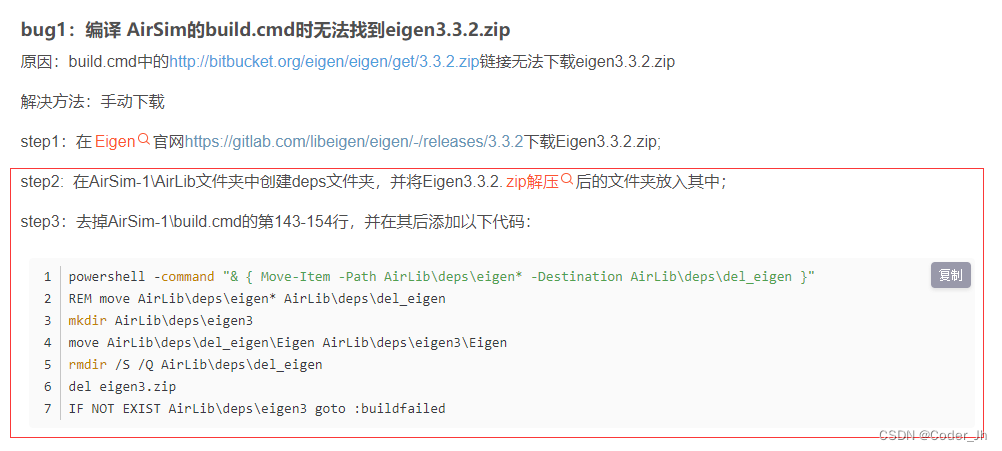
airlearning-ue4安装的踩坑记录
最近要安装airlearning-ue4,用于实现无人机仿真环境,该项目地址为:GitHub - harvard-edge/airlearning-ue4: Environment Generator for Air Learning Project. This version is build on top of UE4 game engine 由于这个项目已经完成好几年…...
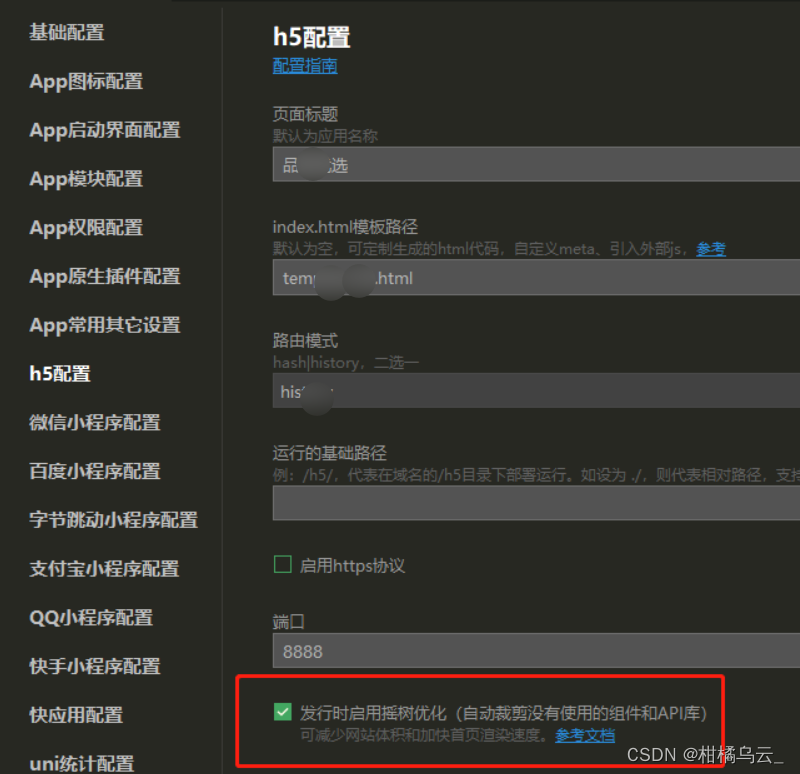
uniapp优化h5项目-摇树优化,gzip压缩和删除console.log
1.摇树优化 勾选摇树优化,打包删除死代码 2.gzip压缩和删除console.log 安装插件webpack和compression-webpack-plugin webpack插件 npm install webpack4.46.0 --save-devcompression-webpack-plugin插件 npm install compression-webpack-plugin6.1.1 --save-devconst Com…...

Pycharm之配置python虚拟环境
最近给身边的人写了脚本,在自己电脑可以正常运行。分享给我身边的人,却运行不起来,然后把报错的截图给我看了,所以难道不会利用pycharm搭建虚拟的环境?记录一下配置的过程。 第一步:右键要打开的python的代…...

如何使用MybatisPlus进行数据分页显示
如何使用MybatisPlus进行数据的分页呢? 使用Mybatis Plus提供的分页插件来简化开发,在MybatisPlusInterceptor的拦截器中添加自动分页的PaginationInnerInterceptor拦截器,当前配置需要交给spring的bean管理,类上添加注解Configu…...

代码随想录 Day49 单调栈01 LeetCode LeetCodeT739每日温度 T496 下一个最大元素I
前言 折磨的死去活来的动态规划终于结束啦,今天秋秋给大家带来两题非常经典的单调栈问题,可能你不清楚单调栈是什么,可以用来解决什么问题,今天我们就来一步一步的逐渐了解单调栈,到能够灵活使用单调栈.注意以下讲解中,顺序的描述为 从栈头到栈底的顺序 什么时候用单…...
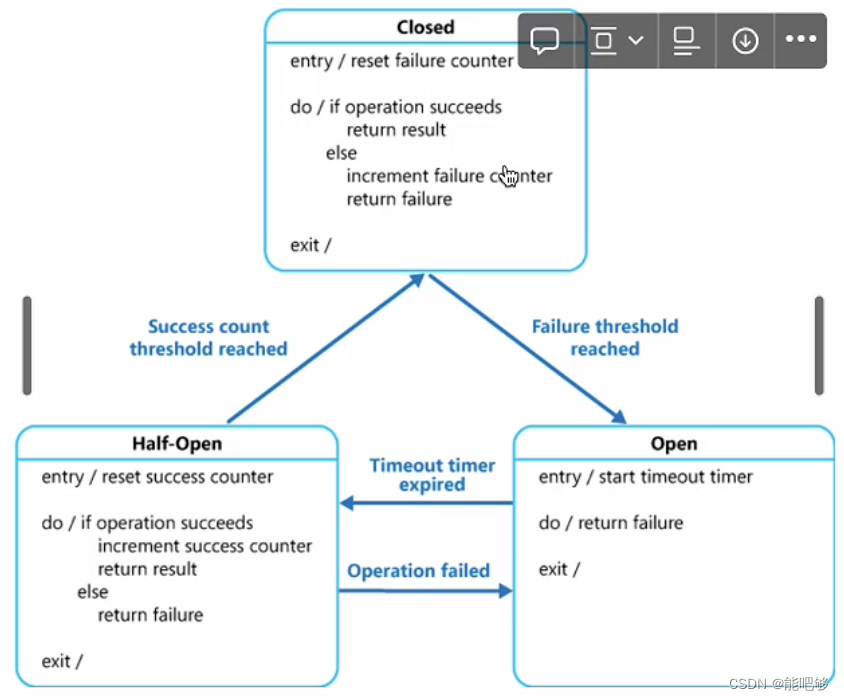
高可用--限流熔断降级
熔断 熔断是应对微服务雪崩效应的一种链路保护机制。 场景 服务端出现问题 服务指标:响应时间、错误率、连续错误数等,超过阈值出发熔断。硬件指标:CPU、网络IO、内存 目的 服务端恢复需要时间、服务端需要休息避免全调用链路崩溃&…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
