【LeetCode刷题日志】225.用队列实现栈

- 🎈个人主页:库库的里昂
- 🎐C/C++领域新星创作者
- 🎉欢迎 👍点赞✍评论⭐收藏
- ✨收录专栏:LeetCode 刷题日志
- 🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,大家一起学习交流!🤗
目录
1.题目描述
2.解题思路+代码实现
方法一:两个队列
思路及算法:
代码实现:
方法二:一个队列
思路及算法:
代码实现:
1.题目描述
OJ链接 【leetcode 题号:225.用队列实现栈】【难度:简单】
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false]解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False
提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty - 每次调用
pop和top都保证栈不为空
进阶:你能否仅用一个队列来实现栈。
2.解题思路+代码实现
方法一:两个队列
思路及算法:
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作,其中q1用于存储栈内的元素,q2作为入栈操作的辅助队列。
入栈操作时,首先将元素入队到q2,然后将q1的全部元素依次出队并入队列q2 ,此时q2的前端的元素即为新入栈的元素,再将q1和q2互换,则q1的元素即为栈内的元素,q1的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保q1的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除q1的前端元素并返回即可,获得栈顶元素操作只需要获得q1的前端元素并返回即可(不移除元素)。
由于q1用于存储栈内的元素,判断栈是否为空时,只需要判断q1是否为空即可。
代码实现:
typedef int QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;void QueueInit(Queue* pq)
{assert(pq);pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}
void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->phead;while (cur) {QNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL) {perror("mallloc fail\n");return;}newnode->data = x;newnode->next = NULL;if (pq->ptail == NULL) {assert(pq->phead == NULL);pq->phead = pq->ptail = newnode;}else {pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->phead->next == NULL) {free(pq->phead);pq->phead = pq->ptail = NULL;}else {QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}
QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}
QDataType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;
}
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}//------以下为OJ提供-------typedef struct {Queue q1;Queue q2;
} MyStack;MyStack* myStackCreate() {MyStack* obj = (MyStack*)malloc(sizeof(MyStack));if (obj == NULL) {perror("malloc fail");return NULL;}QueueInit(&obj->q1);QueueInit(&obj->q2);return obj;
}void myStackPush(MyStack* obj, int x) {if (!QueueEmpty(&obj->q1)) {QueuePush(&obj->q1, x);}else {QueuePush(&obj->q2, x);}
}int myStackPop(MyStack* obj) {Queue* pEmptyQ = &obj->q1;Queue* pNonEmptyQ = &obj->q2;if (!QueueEmpty(&obj->q1)) {pEmptyQ = &obj->q2;pNonEmptyQ = &obj->q1;}while (QueueSize(pNonEmptyQ) > 1) {QueuePush(pEmptyQ, QueueFront(pNonEmptyQ));QueuePop(pNonEmptyQ);}int top = QueueFront(pNonEmptyQ);QueuePop(pNonEmptyQ);return top;
}int myStackTop(MyStack* obj) {if (!QueueEmpty(&obj->q1)) {return QueueBack(&obj->q1);}else {return QueueBack(&obj->q2);}
}bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->q1) &&QueueEmpty(&obj->q2);
}void myStackFree(MyStack* obj) {QueueDestroy(&obj->q1);QueueDestroy(&obj->q2);free(obj);
}复杂度分析
- 时间复杂度:入栈操作O(n),其余操作都是O(1),其中n是栈内的元素个数。 入栈操作需要将q1中的n个元素出队,并入队n+1个元素到q2,共有2n+1次操作,每次出队和入队操作的时间复杂度都是O(1),因此入栈操作的时间复杂度是 O(n)。 出栈操作对应将q1的前端元素出队,时间复杂度是 O(1)。 获得栈顶元素操作对应获得q1的前端元素,时间复杂度是O(1)。 判断栈是否为空操作只需要判断q1是否为空,时间复杂度是 O(1)。
- 空间复杂度:O(n),其中n是栈内的元素个数。需要使用两个队列存储栈内的元素。
方法二:一个队列
思路及算法:
方法一使用了两个队列实现栈的操作,也可以使用一个队列实现栈的操作。
使用一个队列时,为了满足栈的特性,即最后入栈的元素最先出栈,同样需要满足队列前端的元素是最后入栈的元素。
入栈操作时,首先获得入栈前的元素个数 nnn,然后将元素入队到队列,再将队列中的前n个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端的元素即为新入栈的元素,且队列的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保队列的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可,获得栈顶元素操作只需要获得队列的前端元素并返回即可(不移除元素)。
由于队列用于存储栈内的元素,判断栈是否为空时,只需要判断队列是否为空即可。
代码实现:
typedef struct tagListNode {struct tagListNode* next;int val;
} ListNode;typedef struct {ListNode* top;
} MyStack;MyStack* myStackCreate() {MyStack* stk = calloc(1, sizeof(MyStack));return stk;
}void myStackPush(MyStack* obj, int x) {ListNode* node = malloc(sizeof(ListNode));node->val = x;node->next = obj->top;obj->top = node;
}int myStackPop(MyStack* obj) {ListNode* node = obj->top;int val = node->val;obj->top = node->next;free(node);return val;
}int myStackTop(MyStack* obj) {return obj->top->val;
}bool myStackEmpty(MyStack* obj) {return (obj->top == NULL);
}void myStackFree(MyStack* obj) {while (obj->top != NULL) {ListNode* node = obj->top;obj->top = obj->top->next;free(node);}free(obj);
}复杂度分析
- 时间复杂度:入栈操作O(n),其余操作都是O(1),其中n是栈内的元素个数。 入栈操作需要将队列中的n个元素出队,并入队n+1个元素到队列,共有2n+1次操作,每次出队和入队操作的时间复杂度都是O(1),因此入栈操作的时间复杂度是O(n)。 出栈操作对应将队列的前端元素出队,时间复杂度是O(1)。获得栈顶元素操作对应获得队列的前端元素,时间复杂度是O(1)。 判断栈是否为空操作只需要判断队列是否为空,时间复杂度是O(1)。
- 空间复杂度:O(n),其中n是栈内的元素个数。需要使用一个队列存储栈内的元素。

相关文章:

【LeetCode刷题日志】225.用队列实现栈
🎈个人主页:库库的里昂 🎐C/C领域新星创作者 🎉欢迎 👍点赞✍评论⭐收藏✨收录专栏:LeetCode 刷题日志🤝希望作者的文章能对你有所帮助,有不足的地方请在评论区留言指正,…...

【JavaScript】fetch 处理流式数据,实现类 chatgpt 对话
本文只包含最基础的请求后端大佬给得对话接口,大部分模型的传参是差不多的,核心还是如何处理 fetch 获取的流数据 import { defineStore } from pinia; import { ElMessage } from element-plus;type Role system | user | assistant; export interfac…...

收发电子邮件
电子邮件是Internet提供的又一个重要服务项目。早在1987年9月20日,中国首封电子邮件就是从北京经意大利向前联邦德国卡尔斯鲁厄大学发出的,在中国首次实现了与Internet的连接,使中国成为国际互联网大家庭中的一员。现在随着Internet的迅速发展…...
)
sql13(Leetcode570至少有5名直接下属的经理)
代码: 脑子记不住 语法全靠试.. # Write your MySQL query statement below select b.name from (select managerId,count(managerId) as numfrom Employeegroup by managerId ) a left join Employee b on a.managerIdb.id where a.num>5 and b.name is not N…...

15分钟,不,用模板做数据可视化只需5分钟
测试显示,一个对奥威BI软件不太熟悉的人来开发数据可视化报表,要15分钟,而当这个人去套用数据可视化模板做报表,只需5分钟! 数据可视化模板是奥威BI上的一个特色功能板块。用户下载后更新数据源,立即就能获…...

C 语言字符串函数
C 语言字符串函数 在本文中,您将学习使用诸如gets(),puts,strlen()等库函数在C中操作字符串。您将学习从用户那里获取字符串并对该字符串执行操作。 您通常需要根据问题的需要来操作字符串。大多数字符串操作都可以自定义方法完成ÿ…...
nvm安装详细教程(卸载旧的nodejs,安装nvm、node、npm、cnpm、yarn及环境变量配置)
文章目录 一、完全卸载旧的nodejs1、打开系统的控制面板,点击卸载程序,卸载nodejs(1)打开系统的控制面板,点击程序下的卸载程序(2)找到node.js,鼠标右击出现下拉框,点卸载…...
详细步骤记录:持续集成Jenkins自动化部署一个Maven项目
Jenkins自动化部署 提示:本教程基于CentOS Linux 7系统下进行 Jenkins的安装 1. 下载安装jdk11 官网下载地址:https://www.oracle.com/cn/java/technologies/javase/jdk11-archive-downloads.html 本文档教程选择的是jdk-11.0.20_linux-x64_bin.tar.g…...
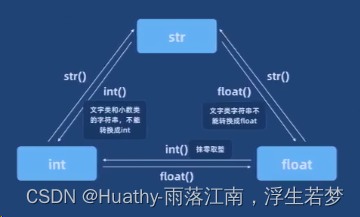
Python学习(一)基础语法
文章目录 1. 入门1.1 解释器的作用1.2 下载1.3 基础语法输入输出语法与引号注释:变量: 数据类型与四则运算数据类型四则运算数据类型的查看type()数据类型的转换int()、int()、float() 流程控制格式化输出循环与遍历逻辑运算符list遍历字典dict遍历 跳出…...

【C刷题】day7
🎥 个人主页:深鱼~🔥收录专栏:【C】每日一练🌄欢迎 👍点赞✍评论⭐收藏 一、选择题 1、以下对C语言函数的有关描述中,正确的有【多选】( ) A: 在C语言中,一…...
数据挖掘复盘——apriori
read_csv函数返回的数据类型是Dataframe类型 对于Dataframe类型使用条件表达式 dfdf.loc[df.loc[:,0]2]df: 这是一个DataFrame对象的变量名,表示一个二维的表格型数据结构,类似于电子表格或SQL表。 df.loc[:, 0]: 这是使用DataFrame的.loc属性来进行…...

Windows10下Maven3.9.5安装教程
文章目录 1.下载maven2.安装3.配置系统变量3.1.新建系统变量 MAVEN_HOME3.2.编辑系统变量Path 4.CMD命令测试是否安装成功5.配置maven本地仓库6.配置国内镜像仓库 1.下载maven 官网 https://maven.apache.org/download.cgi 点击下载。 2.安装 解压到指定目录 D:\installSoft…...

【开源】基于JAVA的校园失物招领管理系统
项目编号: S 006 ,文末获取源码。 \color{red}{项目编号:S006,文末获取源码。} 项目编号:S006,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、研究内容2.1 招领管理模块2.2 寻物管理模块2.3 系…...

requests爬虫IP连接初始化问题及解决方案
问题背景 在使用HTTPS爬虫IP连接时,如果第一次请求是chunked方式,那么HTTPS爬虫IP连接将不会被初始化。这个问题可能会导致403错误,或者在使用HTTPS爬虫IP时出现SSL错误。 解决方案 为了解决这个问题,我们可以在requests库的ada…...
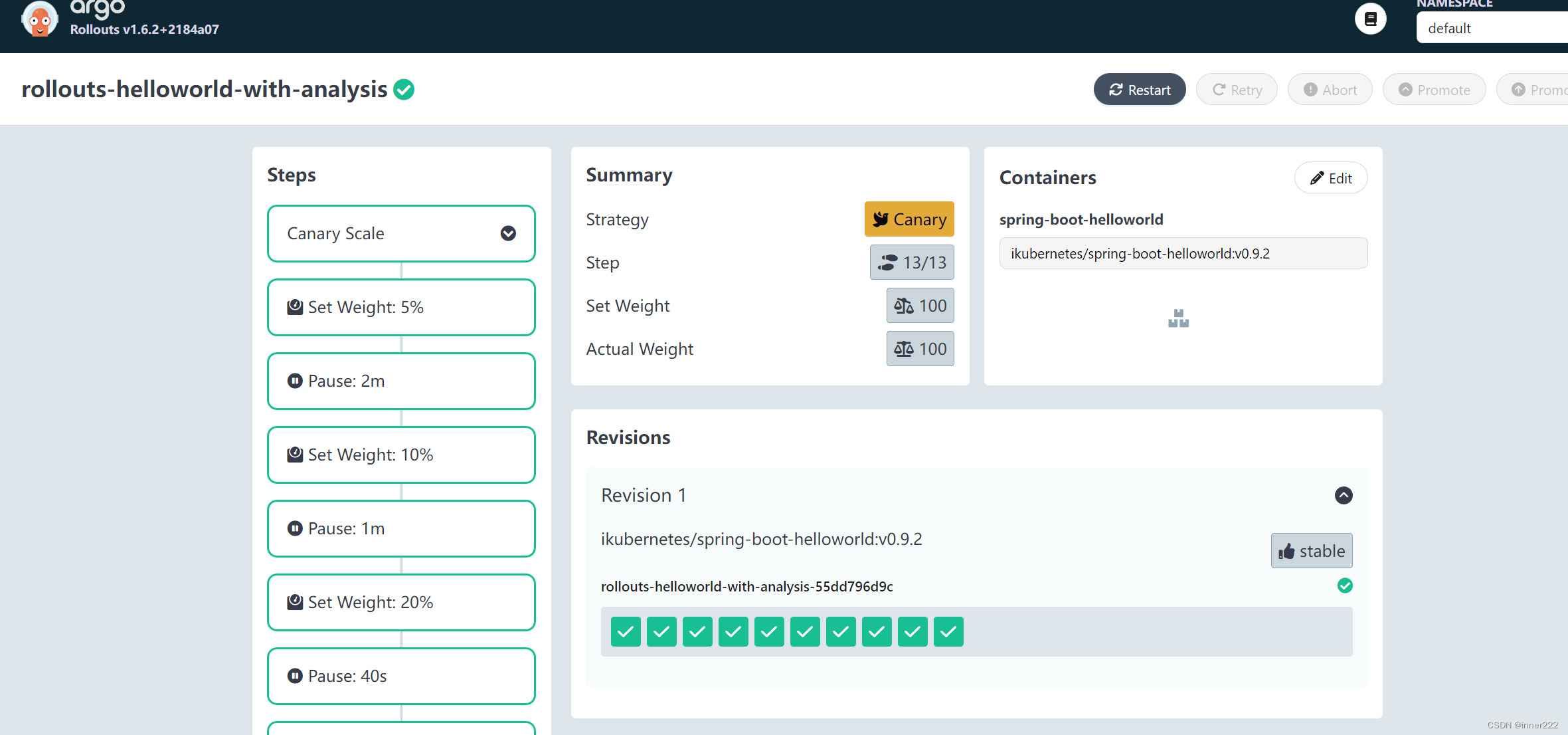
Argo Rollouts结合Service进行Blue-Green部署
删除03 部署04 rootk8s-master01:~/learning-jenkins-cicd/09-argocd-and-rollout/rollout-demos# kubectl delete -f 03-rollouts-with-prometheus-analysis.yaml rootk8s-master01:~/learning-jenkins-cicd/09-argocd-and-rollout/rollout-demos# kubectl apply -f 04-rol…...
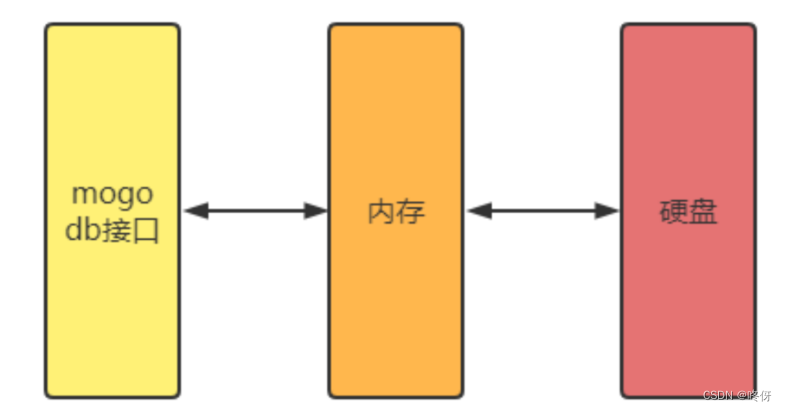
mongodb——原理简介,docker单机部署
MongoDB noSQL数据库 特点 数据文件存储格式为 BSON (JSON 的扩展) {“name”:“joe”}这是 BSON 的例子,其中"name"是键,"joe"是值。键值对组成了 BSON 格式。面向集合…...
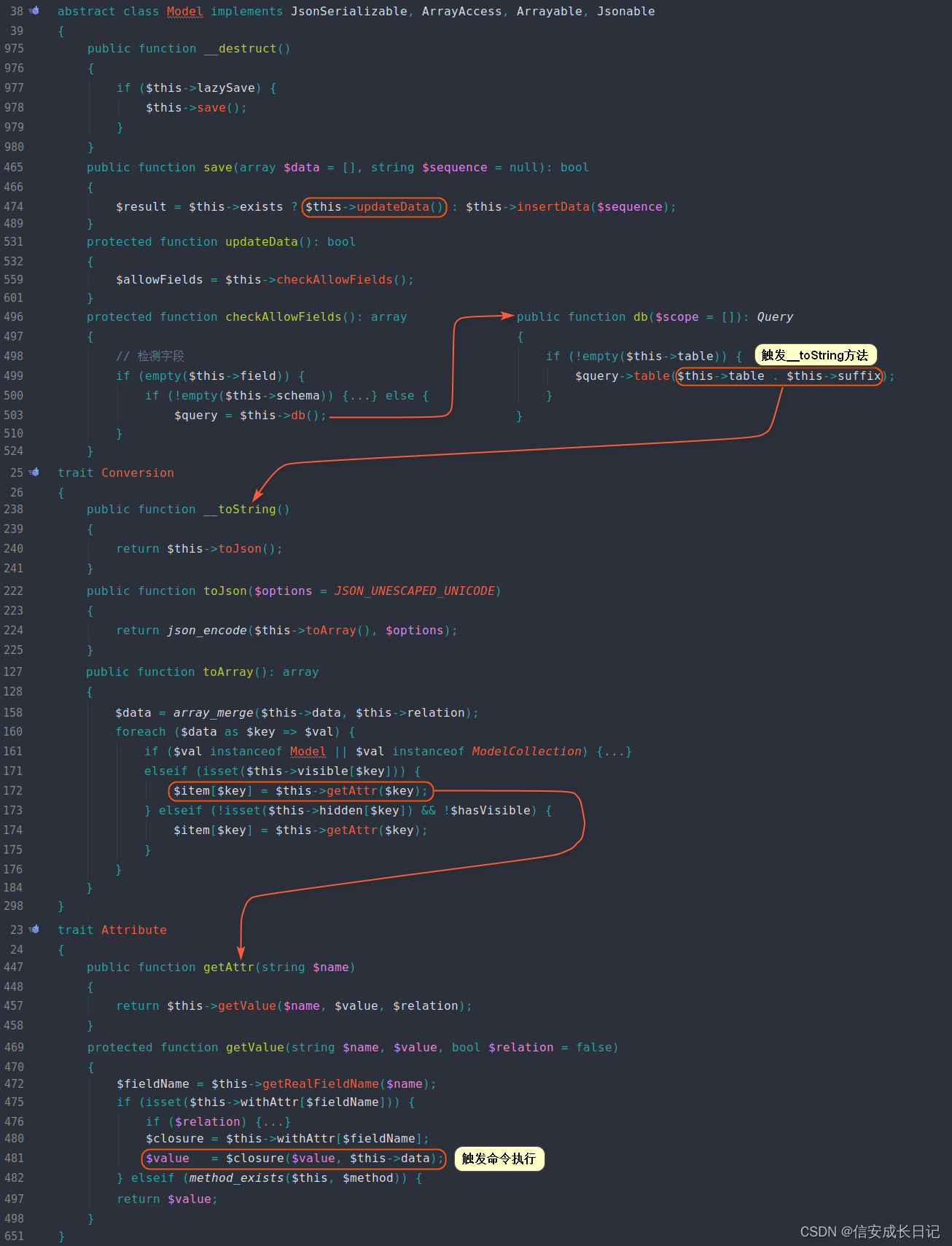
ThinkPHP 系列漏洞
目录 2、thinkphp5 sql注入2 3、thinkphp5 sql注入3 4、 thinkphp5 SQL注入4 5、 thinkphp5 sql注入5 6、 thinkphp5 sql注入6 7、thinkphp5 文件包含漏洞 8、ThinkPHP5 RCE 1 9、ThinkPHP5 RCE 2 10、ThinkPHP5 rce3 11、ThinkPHP 5.0.X 反序列化漏洞 12、ThinkPHP…...

系列十、你说你做过JVM调优和参数配置,请问如何盘点JVM系统的默认值?
一、JVM的参数类型 1.1、标配参数 java -versionjava -help 1.2、XX参数 1.2.1、Boolean类型 公式:-XX:或者- 某个属性值 表示开启、-表示关闭 # 是否打印GC收集细节 -XX:PrintGCDetails -XX:-PrintGCDetails# 是否使用串行垃圾收集器 -XX:UseSerialGC -XX:-UseS…...
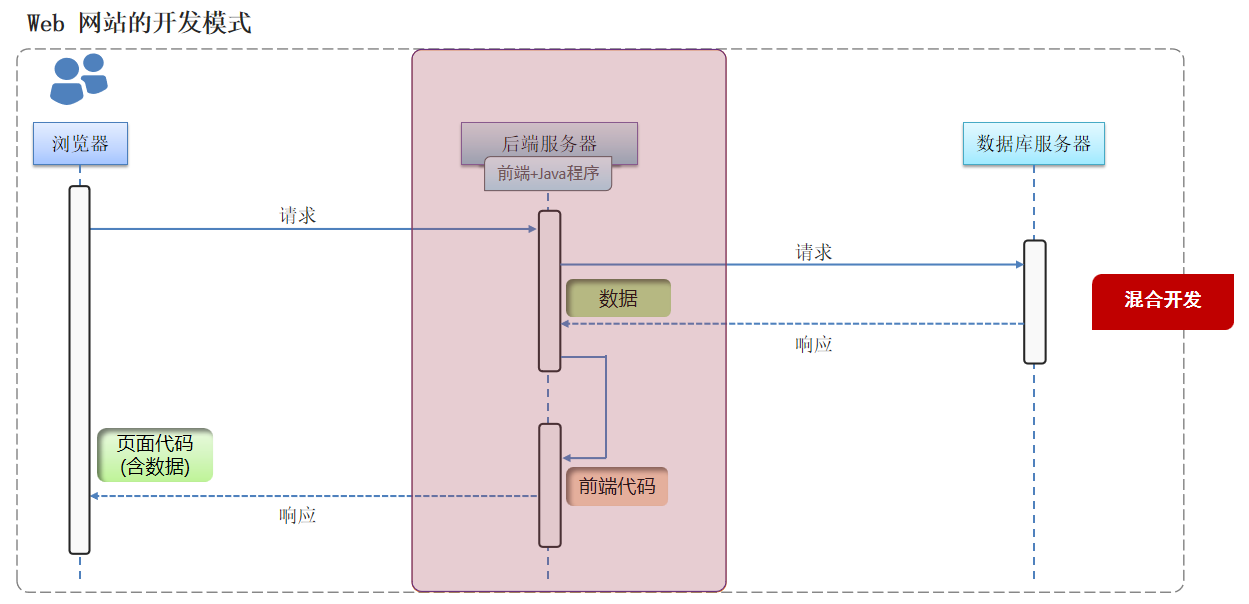
Java Web——Web开发介绍
什么是Web开发 Web开发是一种创建和维护全球广域网(World Wide Web)上的网站和应用的技术。全球广域网也称为万维网(www World Wide Web),是一个能够通过浏览器访问的互联网上的巨大信息库。 Web开发的目标是创建功能齐全、易于使用和安全的…...

Vue 数据监听机制及 Vue 2.0 和 Vue 3.0 的比较
Vue 数据监听机制 在 Vue 中,数据的变化通常是通过数据劫持(Data Binding)和观察者模式来实现的。当数据发生变化时,Vue 能够自动更新视图。 Vue 2.0 的数据监听 在 Vue 2.0 中,数据监听是通过 Object.defineProper…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
