Go常量的定义和使用const,const特性“隐式重复前一个表达式”,以及iota枚举常量的使用
Go常量的定义和使用const,以及iota枚举常量的使用
- Go常量const
- Go中常量的定义和使用
- Go特性const,"隐式重复前一个表达式"
- iota 实现枚举常量
Go常量const
Go语言中的const整合了C语言中的宏定义常量,const只读变量枚举变量
- 绝大多数情况下,Go常量在声明时,并不显示的指定类型
- Go在处理不同类型的变量间的运算时不支持隐式的类型转换,必须进行显示的类型转换。
- Go的无类型常量,拥有字面量的特性。该特性使得无类型常量在参与变量赋值和计算过程中,无需显示的进行类型转换
无类型常量使得go在处理表达式混合数据类型运算时具有很高的灵活性。
Go中常量的定义和使用
定义格式:
const (常量名 = 值......
)
在const代码块中进行对常量的声明,一般使用时,多数使用无类型常量定义。
例如,定义两个无类型常量,在使用时会自动进行类型的隐式转换,很方便:
package main
import "fmt"// 在const代码块中进行常量的声明定义
const (a = 10b = 33.3
)func main() {var number1 int = avar number2 float32 = a + b // 转换成为 float32 数据类型fmt.Println(number1, number2)// 10 43.3fmt.Printf("%T\n%T\n",number1,number2)// int float32
}无类型常量是Go语言推荐的最佳实践,它拥有和字面值一样的灵活性,可以直接用于更多的表达式而不需要显示的进行类型转换。
Go特性const,“隐式重复前一个表达式”
在Go的const语法中,提供了一个“隐式重复前一个表达式”的机制。
package main
import "fmt"
const(blue = 1yellow green blank
)func main(){fmt.Printf("%d\t%d\t%d\t%d\t",blue,yellow,green,blank)\\ 1 1 1 1
}
可以很神奇的发现,在const定义的常量中,如果没有确切的赋值,则会隐式的重复前一个表达式的机制。如上面,我们将blue初始化为1,后续的常量初值并不进行初始化,则其余常量值都会变为1(隐式的重复前一个表达式的机制)。这个机制在iota实现枚举常量中十分常用。
iota 实现枚举常量
iota是Go提供的一个预定义标识符,它在const声明块中每个常量所处位置在块中的偏移,每一行的iota自身都是一个无类型常量,可以像无类型常量那样自动参与不同类型的求值过程,而无须对其进行显示的类型转换。
例如:
package main
import "fmt"
// 使用iota实现go语言中的枚举常量enum
const (n1 = 1 << iotan2n3n4 = iota
)func main() {fmt.Printf("%d\t%d\t%d\t%d\t", n1, n2, n3, n4)// 1 2 4 3
}
分析一波上面的代码:
- 在
n1 = 1<<iota时,n1=1,iota=0 - n2时,由于在const中定义,若未初始化常量值,则会隐式的重复前一个表达式,则
n2 =1<<iota,此时n2=2,iota=1(偏移量为1) - n3时,与n2一致(隐式的重复前一个表达式),
n3=2<<iota,n3=4,iota=2 n4=iota,此时iota的偏移量为4,则n4=4
iota 使得 Go在定义枚举常量时十分灵活和方便:
-
iota预定义标识符可以更为灵活的形式为枚举常量赋值
-
Go的枚举常量不限定于整数值,也可以定义浮点型的枚举常量
-
iota使得维护枚举常量列表更为容易(对比一下传统的常量列表定义和使用iota的const常量定义)
// 不使用iota的传统枚举常量定义 const(n1 = 1n2 = 2n3 = 3n4 = 4 ) // 使用iota的枚举常量定义 const(_ = iotan1 n2n3n4 )当我们需要为常量列表中添加某一个常量时,如果使用第一种传统的方式定义,则需要手动的进行定义和赋值(同时你也需要观察旧的枚举列表,从而对新添加的常量进行赋值),而使用第二种iota时,则可以很灵活的自由添加。
-
使用有类型枚举常量保证类型安全。
相关文章:

Go常量的定义和使用const,const特性“隐式重复前一个表达式”,以及iota枚举常量的使用
Go常量的定义和使用const,以及iota枚举常量的使用Go常量constGo中常量的定义和使用Go特性const,"隐式重复前一个表达式"iota 实现枚举常量Go常量const Go语言中的const整合了C语言中的宏定义常量,const只读变量枚举变量 绝大多数情况下,Go常…...
Git学习(1)pro git阅读
目录 目录: 1. 起步 2. Git 基础 3. Git 分支 4. 服务器上的 Git 5. 分布式 Git 第一章 1.3 Git是什么 1.6运行git前的配置 该开源图书网站 Git - Book (git-scm.com) 目录: 1. 起步 1.1 关于版本控制1.2 Git 简史1.3 Git 是什么?1…...
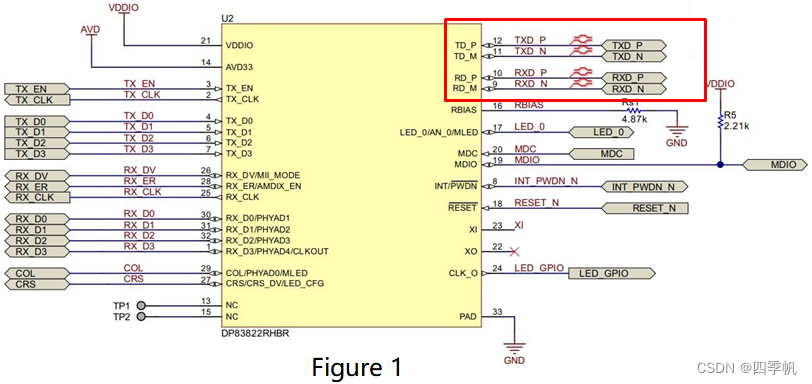
PHY自协商
1. 自协商定义 自动协商模式是端口根据另一端设备的连接速度和双工模式,自动把它的速度调节到最高的公共水平,即线路两端能具有的最快速度和双工模式。 自协商功能允许一个网络设备能够将自己所支持的工作模式信息传达给网络上的对端,并接受对…...

【大数据离线开发】8.2 Hive的安装和配置
8.3 Hive的安装和配置 安装模式: 嵌入模式 :不需要使用MySQL,需要Hive自带的一个关系型数据库:Derby本地模式、远程模式 ----> 需要MySQL数据库的支持 安装 hive 安装包 1、解压tar -zxvf apache-hive-2.3.0-bin.tar.gz -C…...

Capture Modules:车载网络报文捕获模块
(以下所有图片均来源于Technica官网) Technica Engineering的新一代硬件设备,即Capture Modules,提供了五种变体以涵盖不同带宽的车载以太网(100BASE-T1和1000BASE-T1)以及常见的IVN技术(CAN、C…...

数据结构与算法系列之时间与空间复杂度
这里写目录标题算法的复杂度大O的渐进表示法实例分析空间复杂度每日一题算法的复杂度 衡量一个算法的好坏,一般 是从时间和空间两个维度来衡量的, 即时间复杂度和空间复杂度。 时间复杂度主要衡量一个算法的运行快慢, 空间复杂度主要衡量一个…...

Python代码使用PyQt5制作界面并封装
目录参考链接续:https://blog.csdn.net/yulinxx/article/details/93344163 若要对此程序进行封装,加个界面,然后制作成 EXE, 使用 PyQt5 制作界面,PyInstaller 进行封装成 EXE 可参考: Python制作小软件…...
【Node.js】MySQL数据库的第三方模块(mysql)
mysql安装操作MySQL数据库的第三方模块(mysql)通过第三方模块(mysql2)连接到MySQL数据库mysql插入数据mysql插入数据的便捷方式mysql更新数据mysql更新数据的便捷方式mysql删除数据安装操作MySQL数据库的第三方模块(my…...

Docker中安装并配置单机版redis
1、使用docker安装redis 搜索Reis镜像,这里展示的是官方最新的镜像docker search redis 使用官方dockerhub搜索redis 2、选用常用的redis5.0作为安装的版本docker pull redis:5.0 3、运行redis容器的两种方式 3.1 不映射外部配置文件直接运行redis5.0镜像docker …...

模拟微信聊天-课后程序(JAVA基础案例教程-黑马程序员编著-第八章-课后作业)
【案例9-1】 模拟微信聊天 【案例介绍】 1.案例描述 在如今,微信聊天已经人们生活中必不可少的重要组成部分,人们的交流很多都是通过微信来进行的。本案例要求:将多线程与UDP通信相关知识结合,模拟实现微信聊天小程序。通过监…...

html2canvas将页面dom元素内容渲染成图片保存至本地
html2canvas:https://html2canvas.hertzen.com/configuration/ github:https://github.com/niklasvh/html2canvas 效果 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compa…...
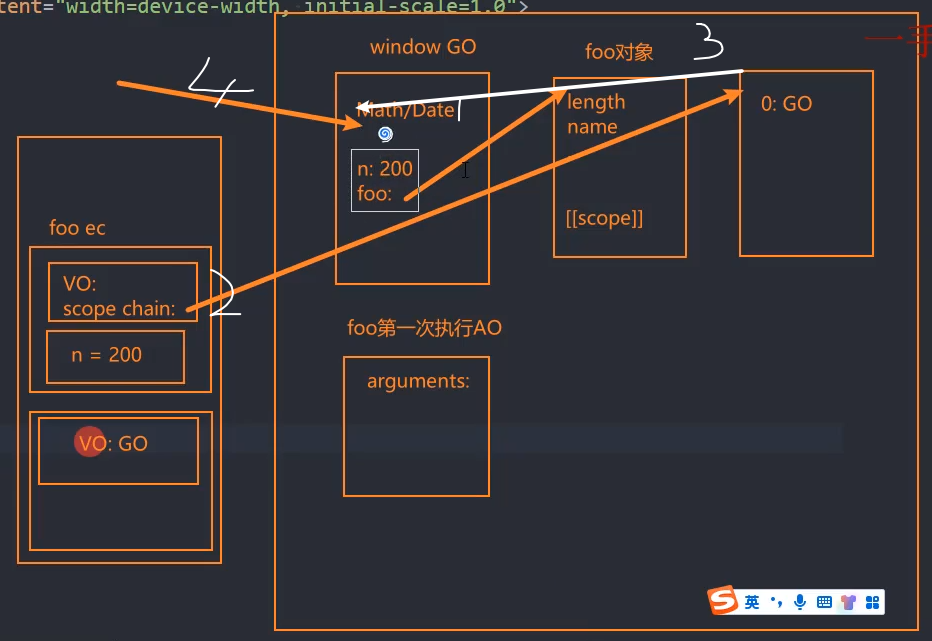
前端进阶JS运行原理
JS运行原理 深入了解V8引擎原理 浏览器内核是由两部分组成的,以webkit为例: WebCore:负责HTML解析、布局、渲染等等相关的工作;JavaScriptCore:解析、执行JavaScript代码; 官方对V8引擎的定义࿱…...
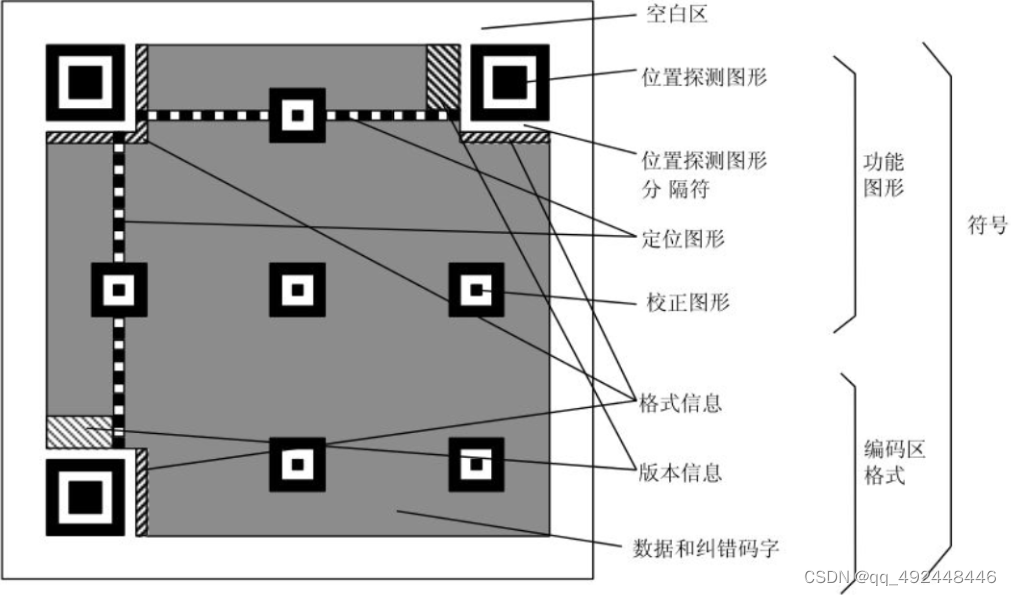
Python识别二维码的两种方法(cv2)
在学习Python处理二维码的过程中,我们看到的大多是“用python生成酷炫二维码”、“用Python制作动图二维码”之类的文章。而关于使用Python批量识别二维码的教程,并不多见。所以今天我会给大家分享两种批量识别二维码的Python技巧!pyzbar PI…...

用一个例子告诉你 怎样使用Spark中RDD的算子
目录 1. 前言 1.1 操作分类 1.2 语法知识 2. transformations 2.1 map 2.2 mapPartitions 2.3 flatMap 2.4 glom 2.5 groupBy 2.6 filter 2.7 sample 2.8 distinct 2.9 coalesce 2.10 repartition 2.11 sortBy 2.12 partitionBy 2.13 reduceByKey 2.14 gro…...
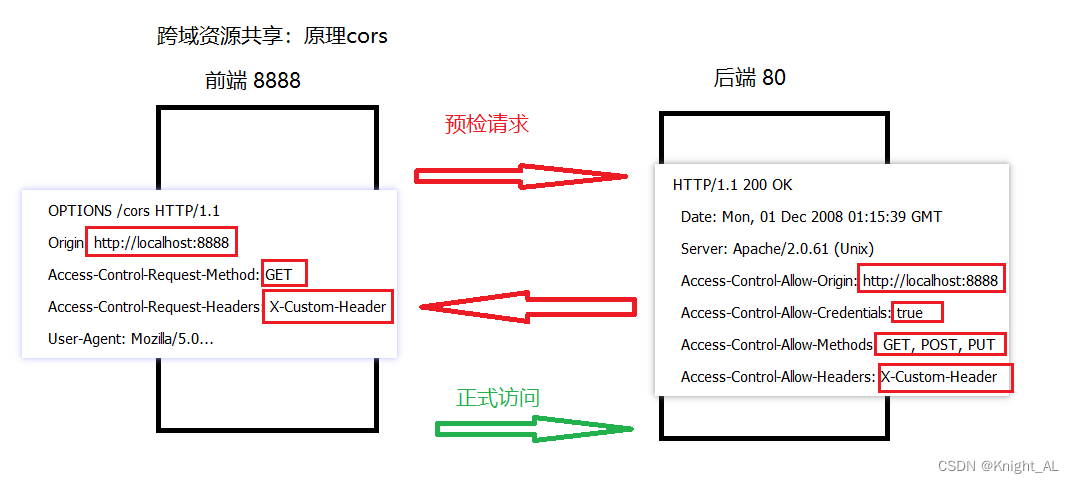
什么是跨域? 出现原因及解决方法
目录一、什么是跨域二、为什么有跨域问题?三、解决跨域问题的方案1.Jsonp2.nginx3.CORS3.1 什么是cors3.2 原理四、GateWay网关中实现跨域步骤一、什么是跨域 跨域:浏览器对于javascript的同源策略的限制 。 同源政策的目的,是为了保证用户…...

低代码系统能够解决哪些痛点?
低代码系统能够解决哪些痛点?如果用4句话去归纳,低代码开发可以解决以下问题—— 为企业提供更高的灵活性,用户可以突破代码的限制自主开发业务应用;通过减少对专业软件开发人员的依赖,公司可以快速响应市场上的新业务…...

华为OD机试题,用 Java 解【两数之和绝对值最小】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

AcWing算法提高课-3.1.1热浪
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 德克萨斯纯朴的民众们这个夏天正在遭受巨大的热浪!!! 他们的德克萨斯长角牛吃起来不错,可是它们并不是很擅长生产富…...

华为OD机试题【最差产品奖】用 C++ 编码,速通 (2023.Q1)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明最差产…...

NFT市场大战:Blur市场地位可持续吗?
在战胜无数虚张声势的挑战者之后,OpenSea终于迎来了一个实力雄厚的竞争对手,已威胁到它的市场主导地位。opensea是什么?参考《NFT,区块链的产物之一,了解NFT交易平台Opensea》 继成功的空投之后,Blur并没有…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
