人工智能及其应用(蔡自兴)期末复习
人工智能及其应用(蔡自兴)期末复习
相关资料:
人工智能期末复习
人工智能复习题
人工智能模拟卷
人工智能期末练习题
1 ⭐️绪论
人工智能:人工智能就是用人工的方法在机器(计算机)上实现的智能,或称机器智能、计算机智能。
人工智能发展的三个阶段:
- 计算
- 感知
- 认知
⭐️人工智能发展时期:
-
孕育期 ( 1956年前):亚里士多德,莱布尼茨,图灵,莫克,麦克洛奇和皮兹,维纳
-
形成期 ( 1956-1970年):1956年第一次人工智能研讨会(达特茅斯会议),
-
暗淡期 ( 1966-1974年):过高预言
-
知识应用期 ( 1970-1988年):专家系统的出现
-
集成发展期 ( 1986年至今):AI技术进一步研究
⭐️人工智能学派:
- 符号主义(功能模拟方法):逻辑主义,以物理符号系统为原理,代表:纽厄尔,肖,西蒙,尼尔逊(诺艾尔,魈,派蒙,泥鳅)(诺艾尔打架溅了一身泥,被魈卷到天上,突然击中了派蒙)
- 连接主义(结构模拟方法):仿生学派,神经网络之间连接机制为原理,代表:卡洛克,皮茨,霍普菲尔德,鲁梅尔哈特
- 行为主义(行为模拟方法):控制论学派,类似于控制机器人,代表:布鲁克斯
人工智能应用:问题求解和博弈,逻辑推理和定理证明,计算智能,分布式人工智能和真体,自动程序设计,专家系统,机器学习,自然语言理解,机器人学,模式识别,机器视觉,神经网络,智能控制
人工智能系统分类:专家系统,模糊系统,神经网络系统,学习系统,仿生系统,群智能系统,多真体系统,混合智能系统
目标:
- 近期目标:建造智能计算机代替人类的部分智力劳动
- 远期目标:揭示人类智能的根本机理,用智能机器去模拟、延伸和扩展人类的智能
研究的基本内容:认知建模,知识表示,知识推理,知识应用,机器感知,机器思维,机器学习,机器行为,智能系统构建
2 知识表示
2.1 ⭐️状态空间表示
概念理解:状态,算符
状态表示(知道初始状态和目标状态),状态表示图的画法
相关问题:
- 野人传教士渡河问题
(a,b,c)(a, b, c)(a,b,c)表示(左岸传教士人数,左岸野人数,左岸船数)
- 梵塔问题
状态:(SA,SB)(S_A, S_B)(SA,SB),SAS_ASA表示AAA所在杆号,SBS_BSB表示BBB所在杆号,SA,SB∈{1,2,3}S_A,S_B \in \{1, 2, 3\}SA,SB∈{1,2,3},全部状态为:
(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)(1,1), (1, 2), (1, 3), (2, 1), (2, 2),(2,3),(3,1),(3,2),(3,3) (1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)
初始状态:(1,1)(1,1)(1,1),目标状态:(3,3)(3,3)(3,3)
状态空间图:

- 八数码问题
2.2 ⭐️归约表示(与或图)
需要理解:归约表示思路,与或图表示
- 梵塔问题(四阶为例)
假设用向量(D4,D3,D2,D1)(D_4, D_{3},D_2, D_1)(D4,D3,D2,D1)表示从大到小的圆盘所在的柱子号,则
初始状态:(1,1,1,1)(1, 1, 1, 1)(1,1,1,1)
目标状态:(3,3,3,3)(3, 3, 3, 3)(3,3,3,3)
问题归约为子问题:
- 移动3,2,1号圆盘至2号柱子
- 移动4号圆盘至3号柱子
- 移动3,2,1号圆盘至3号柱子
归约图表示:
2.3 谓词逻辑表示
概念理解:谓词,项,谓词公式,原子公式,合式公式
合式公式性质:

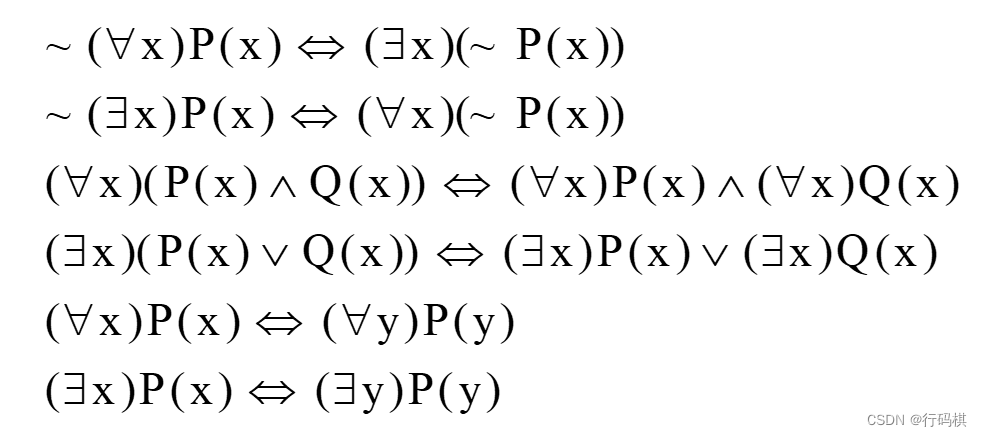
自然语言转换成谓词:
-
人都会死
(∀x)(man(x)→die(x))(\forall x) (man(x) \to die(x)) (∀x)(man(x)→die(x)) -
有的人聪明
(∃x)(man(x)→clever(x))(\exist x) (man(x) \to clever(x)) (∃x)(man(x)→clever(x))
谓词推理:
下面的例子使用了P∨Q¬P∨Q⟹Q∨Q=QP \lor Q \hspace{1em} \neg P \lor Q \implies Q \lor Q = QP∨Q¬P∨Q⟹Q∨Q=Q 消解推理规则

2.4 语义网络表示
常用语义联系:


推理机制:匹配和继承
2.5 框架表示
结构:
- 节点
- 槽:每个槽可有多个侧面,每个侧面可有多个值
- 值
推理机制:
- 匹配
- 填槽(查询,默认,继承,附加过程计算)
大学教师的框架:

2.6 ⭐️知识表示方法的联系

3 搜索推理
3.1 ⭐️盲目搜索(无信息搜索)
本小节没有加以整理,请看课件
- ⭐️深度优先搜素
- ⭐️宽(广)度优先搜索
- 等代价搜索(UCS):就是
Dijkstra算法 - 有界深搜:就是限制深度的深搜
- 迭代加深算法(IDS)
知道OPEN表和CLOSED表的作用
3.2 ⭐️启发式搜索(有信息搜索)
按选择范围不同分为:全局择优搜索(A,A*)和局部择优搜素
f(x)=g(x)+h(x)f(x) = g(x) + h(x) f(x)=g(x)+h(x)
h(x)h(x)h(x):启发函数
搜索算法:
-
A算法:h(x)h(x)h(x)不做限制 -
A*算法:h(x)h(x)h(x)有限制
3.3 ⭐️消解原理(归结原理)
就是对几个子句推导出新的子句(几个公理推导出新的结论)
- ⭐️如何求子句集(将谓词演算公式化成子句集)P97
子句集特征:没有蕴涵词(→\rightarrow→)、等值词(↔,≡\leftrightarrow, \equiv↔,≡),¬\neg¬作用原子谓词,没有全称和存在量词,合取范式,元素之间变元不同,集合形式

- ⭐️消解推理规则
P¬P∨Q⟹QP∨Q¬P∨Q⟹Q∨Q=Q¬PP⟹NIL¬P∨R(P→R)¬Q∨R(Q→R)⟹¬P∨Q(P→Q)P \hspace{1em} \neg P \lor Q \implies Q \\ P \lor Q \hspace{1em} \neg P \lor Q \implies Q \lor Q = Q \\ \neg P \hspace{1em} P \implies NIL \\ \neg P \lor R(P \to R) \hspace{1em} \neg Q \lor R(Q \to R) \implies \neg P \lor Q(P \to Q) P¬P∨Q⟹QP∨Q¬P∨Q⟹Q∨Q=Q¬PP⟹NIL¬P∨R(P→R)¬Q∨R(Q→R)⟹¬P∨Q(P→Q)
- 消解反演
消解通过反演来证明。将目标公式否定添加到命题公式集中,从中推导出一个空子句。(类似于反证法,否定结论,并将其作为条件,推导出一个空结论,即不可能满足的结论)
反演树的画法与理解
- 置换与合一的概念
置换:σ={f(a)/x,f(y)/z}\sigma = \{f(a) / x , f(y) / z\}σ={f(a)/x,f(y)/z} 代表用f(a)f(a)f(a)代替掉xxx,用f(y)f(y)f(y)代替掉zzz。
合一:寻找一个置换,使两个表达式一致的过程。
3.4 规则演绎
- 产生式系统
产生式规则一般形式:
IFA1,A2,...,AnTHENBIF \hspace{1em} A_1,A_2,...,A_n \hspace{1em} THEN \hspace{1em} BIFA1,A2,...,AnTHENB
逻辑蕴含式是产生式的一种特殊形式。
产生式系统的组成:
- 总数据库
- 产生式规则(规则库)
- 控制策略(推理机)
产生式系统的推理:正向推理,逆向推理,双向推理。
3.5 不确定性推理
三种不确定性程度:
- 知识不确定性
- 证据不确定性
- 结论不确定性
不确定性表示度量:
- 静态强度:知识的不确定性程度表示,(LS,LN)为知识的不确定性表示。
- 动态强度:证据的不确定性程度表示
3.5.1 ⭐️概率推理
条件概率公式:
P(A∣B)=P(AB)P(B)P(A|B) = \frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
全概率公式:(AiA_iAi构成一个完备事件组,互相独立,其总和为全集)
P(B)=∑i=1nP(Ai)P(B∣Ai)P(B) = \sum \limits_{i = 1}^n P(A_i)P(B|A_i) P(B)=i=1∑nP(Ai)P(B∣Ai)
贝叶斯公式:(先验概率P(H)P(H)P(H),条件概率P(H∣E)P(H|E)P(H∣E))
P(H∣E)=P(H)P(E∣H)P(E)P(Bi∣A)=P(Bi)P(A∣Bi)∑iP(Bi)P(A∣Bi)P(Hi∣E1E2⋯Em)=P(E1∣Hi)P(E2∣Hi)⋯P(Em∣Hi)P(Hi)∑j=1nP(E1∣Hj)P(E2∣Hj)⋯P(Em∣Hj)P(Hj)P(H|E) = \frac{P(H)P(E|H)}{P(E)} \\ P(B_i | A) = \frac{P(B_i)P(A|B_i)}{\sum_i P(B_i) P(A|B_i)} \\ P(H_i | E_1E_2 \cdots E_m) = \frac{P(E_1|H_i)P(E_2|H_i) \cdots P(E_m|H_i)P(H_i)}{\sum \limits_{j = 1}^n P(E_1|H_j)P(E_2|H_j) \cdots P(E_m|H_j)P(H_j)} P(H∣E)=P(E)P(H)P(E∣H)P(Bi∣A)=∑iP(Bi)P(A∣Bi)P(Bi)P(A∣Bi)P(Hi∣E1E2⋯Em)=j=1∑nP(E1∣Hj)P(E2∣Hj)⋯P(Em∣Hj)P(Hj)P(E1∣Hi)P(E2∣Hi)⋯P(Em∣Hi)P(Hi)

3.5.2 主观贝叶斯(?)

相关公式:
O(X)=P(X)1−P(X)O(H∣E)=LS⋅O(H)O(H∣¬E)=LN⋅O(H)O(H∣S1,S2,⋯,Sn)=O(H∣S1)O(H)⋅O(H∣S2)O(H)⋯O(H∣Sn)O(H)⋅O(H)O(X) = \frac{P(X)}{1 - P(X)} \\ O(H|E) = LS \cdot O(H) \\ O(H| \neg E) = LN \cdot O(H) \\ O(H|S_1, S_2, \cdots, S_n) = \frac{O(H|S_1)}{O(H)} \cdot \frac{O(H|S_2)}{O(H)} \cdots \frac{O(H|S_n)}{O(H)} \cdot O(H) O(X)=1−P(X)P(X)O(H∣E)=LS⋅O(H)O(H∣¬E)=LN⋅O(H)O(H∣S1,S2,⋯,Sn)=O(H)O(H∣S1)⋅O(H)O(H∣S2)⋯O(H)O(H∣Sn)⋅O(H)
EH公式:
P(H∣S)={P(H∣¬E)+P(H)−P(H∣¬E)P(E)×P(E∣S)0≤P(E∣S)<P(E)P(H)+P(H∣E)−P(H)1−P(E)×(P(E∣S)−P(E))P(E)≤P(E∣S)≤1(1)P(H|S) = \begin{cases} P(H| \neg E) + \frac{P(H) - P(H|\neg E)}{P(E)} \times P(E|S) & 0 \le P(E|S) \lt P(E) \\ P(H) + \frac{P(H|E) - P(H)}{1 - P(E)} \times (P(E|S) - P(E)) & P(E) \le P(E|S) \le 1 \end{cases} \hspace{2em} (1) P(H∣S)={P(H∣¬E)+P(E)P(H)−P(H∣¬E)×P(E∣S)P(H)+1−P(E)P(H∣E)−P(H)×(P(E∣S)−P(E))0≤P(E∣S)<P(E)P(E)≤P(E∣S)≤1(1)
CP公式:
P(H∣S)={P(H∣¬E)+(P(H)−P(H∣¬E))×(15C(E∣S)+1)C(E∣S)≤0P(H)+(P(H∣E)−P(H))×15C(E∣S)C(E∣S)>0(2)P(H|S) = \begin{cases} P(H| \neg E) + (P(H) - P(H|\neg E)) \times (\frac{1}{5}C(E|S) + 1) & C(E|S) \le 0 \\ P(H) + (P(H|E) - P(H)) \times \frac{1}{5}C(E|S) & C(E|S) \gt 0 \end{cases} \hspace{2em} (2) P(H∣S)={P(H∣¬E)+(P(H)−P(H∣¬E))×(51C(E∣S)+1)P(H)+(P(H∣E)−P(H))×51C(E∣S)C(E∣S)≤0C(E∣S)>0(2)
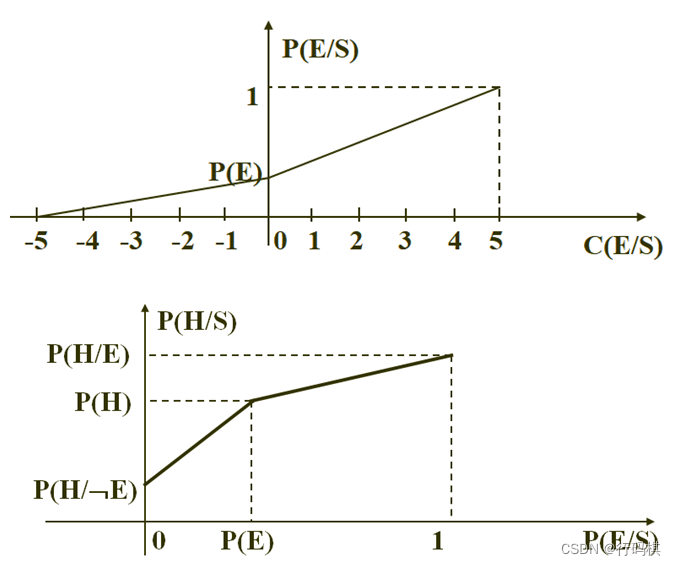
根据第一张图得到P(E∣S)P(E|S)P(E∣S)与C(E∣S)C(E|S)C(E∣S)的关系,记为式(3)(3)(3)
根据第二张图得到P(H∣S)P(H|S)P(H∣S)与P(E∣S)P(E|S)P(E∣S)的关系,即为式(1)(1)(1)
将式(3)(3)(3)代入到式(1)(1)(1)中,得到CP公式

3.5.3 ⭐️可信度方法
可信度表示知识或证据的不确定性,范围[−1,1][-1,1][−1,1]
知识的不确定性表示:
if E then H (CF(H, E))
CF(H,E):是该条知识的可信度,称为可信度因子或规则强度,它指出当前提条件 E 所对应的证据为真时,它对结论为真的支持程度。


推理结论CF值计算:
CF(H)=CF(H,E)×max{0,CF(E)}CF(H) = CF(H, E) \times max\{0, CF(E) \} CF(H)=CF(H,E)×max{0,CF(E)}
重复结论CF值计算:
ifE1thenH(CF(H,E1))ifE2thenH(CF(H,E2))则CF1,2(H)={CF1(H)+CF2(H)−CF1(H)×CF2(H)CF1(H)≥0,CF2(H)≥0CF1(H)+CF2(H)+CF1(H)×CF2(H)CF1(H)<0,CF2(H)<0CF1(H)+CF2(H)1−min{∣CF1(H)∣,∣CF2(H)∣}CF1(H),CF2(H)异号if \hspace{1em} E_1 \hspace{1em} then \hspace{1em} H \hspace{1em} (CF(H,E_1)) \\ if \hspace{1em} E_2 \hspace{1em} then \hspace{1em} H \hspace{1em} (CF(H,E_2)) \\ \text{则} CF_{1,2}(H) = \begin{cases} CF_1(H) + CF_2(H) - CF_1(H) \times CF_2(H) & CF_1(H) \ge 0, CF_2(H) \ge 0 \\ CF_1(H) + CF_2(H) + CF_1(H) \times CF_2(H) & CF_1(H) \lt 0, CF_2(H) \lt 0 \\ \frac{CF_1(H) + CF_2(H)}{1 - min\{ |CF_1(H)|, |CF_2(H)|\}} & CF_1(H),CF_2(H) \text{异号} \end{cases} ifE1thenH(CF(H,E1))ifE2thenH(CF(H,E2))则CF1,2(H)=⎩⎨⎧CF1(H)+CF2(H)−CF1(H)×CF2(H)CF1(H)+CF2(H)+CF1(H)×CF2(H)1−min{∣CF1(H)∣,∣CF2(H)∣}CF1(H)+CF2(H)CF1(H)≥0,CF2(H)≥0CF1(H)<0,CF2(H)<0CF1(H),CF2(H)异号
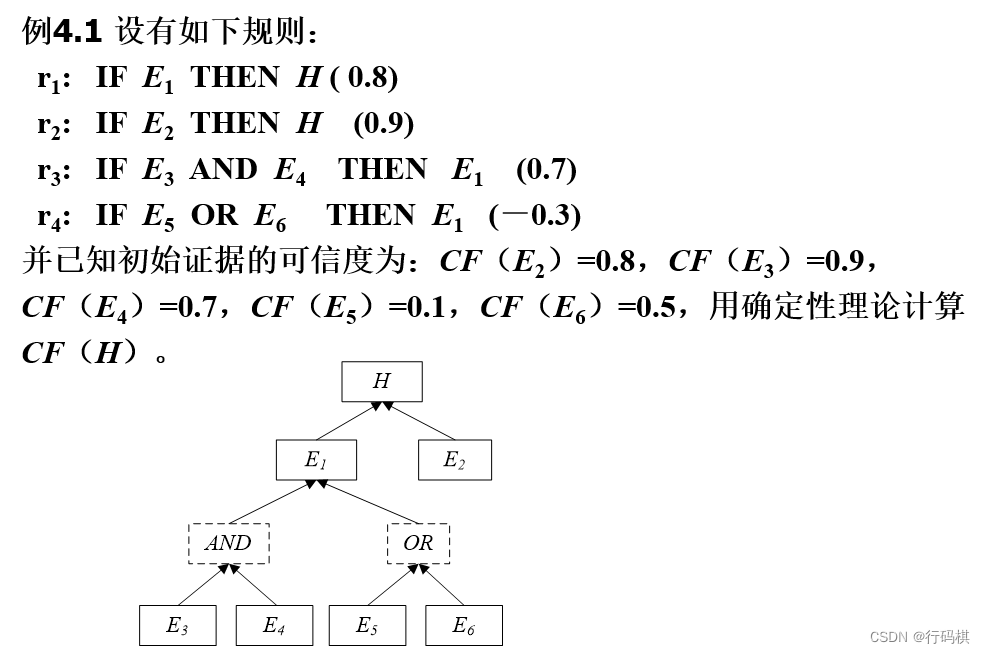

4 计算智能
4.1 神经计算
神经网络三要素:
-
神经元
- 为一个简单的线性阈值单元(阈值逻辑单元TLU),简单的单层前馈网络,叫感知器
- 多个输入通过f(∑i=1nwixi−θ)f(\sum \limits_{i = 1}^n w_i x_i - \theta)f(i=1∑nwixi−θ)输出,fff称为变换函数,θ\thetaθ称为阈值或偏差。
-
网络拓扑结构
- 递归(反馈)网络(多个神经元之间组成一个互连神经网络)
- 前馈(多层)网络(神经元之间不存在互连)(代表:BP网络(梯度下降法))
-
学习算法
-
有师学习算法
-
无师学习算法(无需知道期望输出)
- 聚类算法
-
强化学习算法
- 遗传算法
-
感知器逻辑推理:
- 可以解决
AND, OR, NOT问题 - 不可解决线性不可分问题,例如
XOR问题 - 但XOR可以使用多层感知器网络(前馈网络)和递归网络实现
4.2 模糊计算
4.2.1 表示
A={(x,μA(x))∣x∈U}A = \{ (x, \mu_A(x)) |x \in U \} A={(x,μA(x))∣x∈U}
μA(x)\mu_A(x)μA(x) :xxx对AAA的隶属度,μA(x)∈[0,1]\mu_A(x) \in [0, 1]μA(x)∈[0,1]
表示:
-
XXX为离散域
F=∑i=1nμF(x)/xA=0/1+0.1/2+0.5/3+0.8/4+1/5或F={μF(u1),μF(u2),⋯,μF(un)}A={0,0.1,0.5,0.8,1}F = \sum \limits_{i = 1}^n \mu _F(x) / x \hspace{1em} A = 0/1 + 0.1/2 + 0.5/3 + 0.8 / 4 + 1/5 \\ \text{或} \\ F = \{\mu_F(u_1), \mu_F(u_2), \cdots, \mu_F(u_n) \} \hspace{1em} A = \{0, 0.1, 0.5, 0.8, 1 \} F=i=1∑nμF(x)/xA=0/1+0.1/2+0.5/3+0.8/4+1/5或F={μF(u1),μF(u2),⋯,μF(un)}A={0,0.1,0.5,0.8,1} -
XXX 为连续域
F=∫XμF(x)/xF = \int_X \mu_F(x) / x F=∫XμF(x)/x
4.2.2 模糊运算
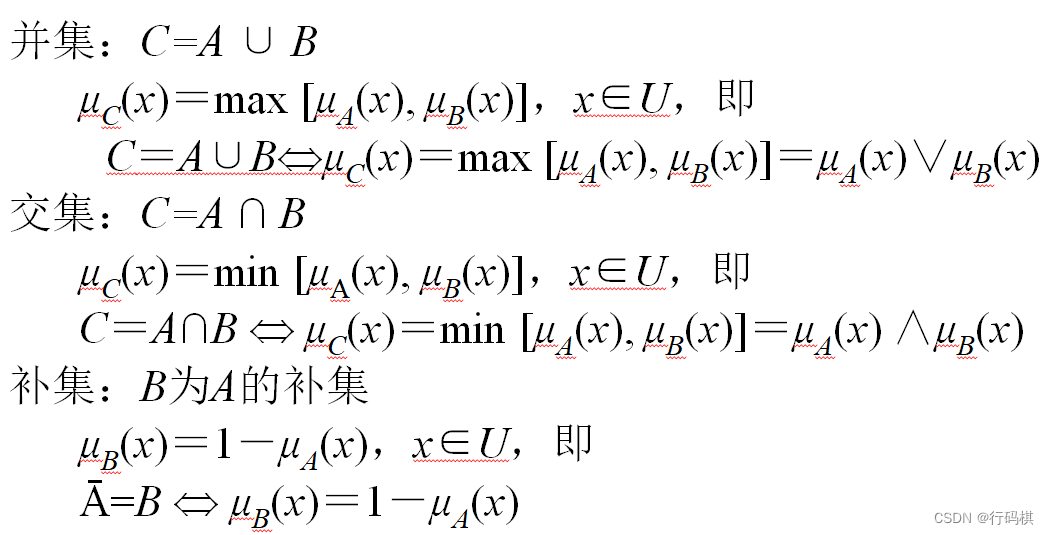
4.2.3 原理(求解过程)
- 模糊化
- 模糊计算:模糊统计法,对比排序法,专家评判法
- 模糊判决(解模糊):重心法,最大隶属度法,系统加权平均法,隶属度限幅元素平均法
4.3 ⭐️遗传算法
- 是一种模仿生物遗传学和自然选择机理的优化搜索算法,是进化计算的一种重要的形式。有选择算子,交叉算子,变异算子。
- 流程
- 初始化群体,群体中的每一个个体都是染色体,由二进制串组成,所以算法中会牵扯到编码和解码操作
- 计算所有个体的适应度(适应度函数由用户自定义,保证适应度大的个体质量更好)
- 选择:选择方法一般有赌轮选择和联赛选择。赌轮选择:每个个体有一个选择的概率,可以定为个体的适应度除以群体总的适应度,产生随机数选择一个个体。联赛选择:随机选择m个个体,选择适应度最大的个体。选择之后要进行解码操作。
- 以某一概率进行交叉。(交叉分为一点交叉和两点交叉)
- 以某一概率进行突变
- 直至满足某种停止条件,否则一直进行适应度计算往下的操作
- 输出适应度最优的染色体作为最优解
4.4 ⭐️粒群优化算法(?)
迭代公式
速度更新公式:
v(t+1)=wv(t)+c1rand()(pi−x(t))+c2rand()(pg−x(t))v(t + 1) = wv(t) + c_1rand() (p_i - x(t)) + c_2rand()(p_g - x(t)) v(t+1)=wv(t)+c1rand()(pi−x(t))+c2rand()(pg−x(t))
www :惯性权重,c1,c2c_1,c_2c1,c2 :加速常数,pip_ipi :个体极值,pgp_gpg :全局极值
位置更新公式:x(t+1)=x(t)+v(t+1)x(t + 1) = x(t) + v(t + 1)x(t+1)=x(t)+v(t+1)
5 机器学习
5.1 归纳学习
分为:
- 有师学习(示例学习)
- 无师学习(观察发现学习)
5.2 神经网络学习
BP算法:反向传播算法
学习过程:正向传播 + 反向传播
5.3 深度学习
定义:将神经-中枢-大脑的工作原理设计成一个不断迭代、不断抽象的过程,以便得到最优数据特征表示的机器学习算法
卷积神经网络:
- 神经元之间非全连接
- 同一层神经元之间采用权值共享的方式
优点:
- 采用非线性处理单元组成的多层结构
- 分为有监督学习和无监督学习
- 学习无标签数据优势明显
常用模型:
- 自动编码器:无监督学习
- 受限玻尔兹曼机:学习概率分布的一个随机生成神经网络,限定模型必须为二分图
- 深度信念网络:靠近可视层部分使用贝叶斯信念网络
- 卷积神经网络:多个卷积层和全连接层组成
5.4 ⭐️决策树
可参考:https://wyqz.top/p/808139430.html#toc-heading-34
信息熵:
Ent(X)=−∑pilog2pii = 1, 2, …, nEnt(X) = - \sum p_i log_2 p_i \hspace{2em} \text{i = 1, 2, …, n} Ent(X)=−∑pilog2pii = 1, 2, …, n
信息增益: 表示特征XXX使得类YYY的不确定性减少的程度(熵值减少),即当前划分对信息熵所造成的变化。
信息增益越大,表示特征a来划分所减少的熵最大,即提升最大,应当作为根节点。
Gain(S,A)=Ent(S)−∑v∈values(A)∣Sv∣∣S∣Ent(Sv)Gain(S, A) = Ent(S) - \sum \limits_{v \in values(A)} \frac{|S_v|}{|S|} Ent(S_v) Gain(S,A)=Ent(S)−v∈values(A)∑∣S∣∣Sv∣Ent(Sv)
基于信息增益的ID3算法的实例:
我们有14天的数据,4个特征条件:天气,温度,湿度,是否有风。最终结果是去玩不玩。

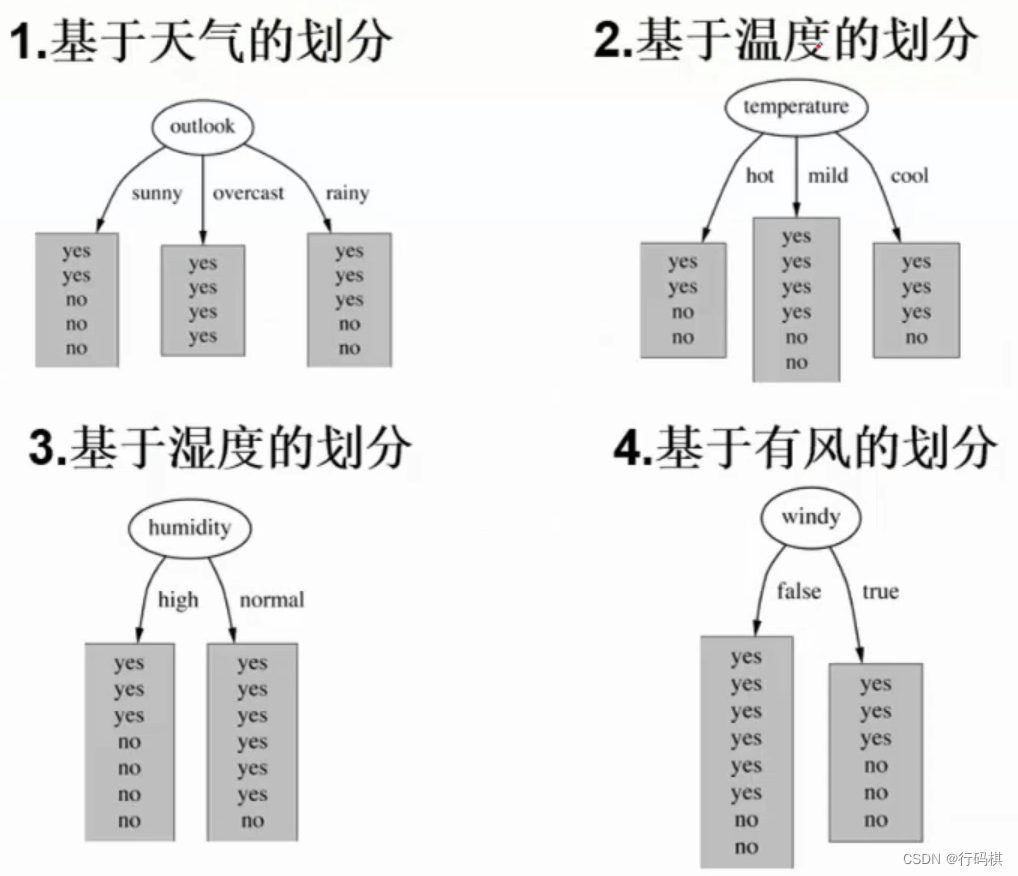
上面有四种划分方式,我们需要判断谁来当根节点,根据的主要就是信息增益这个指标。下面计算信息增益来判断根节点。
总的数据中,9天玩,5天不玩,熵值为:
−914log2914−514log2514=0.940-\frac{9}{14}log_2 \frac{9}{14} - \frac{5}{14}log_2 \frac{5}{14} = 0.940 −149log2149−145log2145=0.940
本例暂且以ent(a, b)代表以下含义:(只有两种结果的时候的熵值计算)
from math import log2
def ent(a, b):tot = a + bx, y = a / tot, b / totreturn -(x * log2(x) + y * log2(y))
然后对4个特征逐个分析:
-
outlook
outlook = sunny时,熵值为0.971,取值为sunny的概率为 514\frac{5}{14}145outlook = overcast时,熵值为0,取值为overcast的概率为 414\frac{4}{14}144outlook = rainy时,熵值为0.971,取值为rainy的概率为 514\frac{5}{14}145
熵值为:
514×0.971+414×0+514×0.971=0.693\frac{5}{14} \times 0.971 + \frac{4}{14} \times 0 + \frac{5}{14} \times 0.971 = 0.693 145×0.971+144×0+145×0.971=0.693
信息增益:系统熵值从0.940下降到0.693,增益为0.247。 -
temperture
temperture = hot时,熵值为1.0(ent(2, 2)),取值为hot的概率为414\frac{4}{14}144temperture = mild时,熵值为0.918(ent(4, 2)),取值为mild的概率为614\frac{6}{14}146temperture = cool时,熵值为0.81(ent(3,1)),取值为cool的概率为414\frac{4}{14}144
熵值为:
414×1.0+614×0.918+414×0.81=0.911\frac{4}{14} \times 1.0 + \frac{6}{14} \times 0.918 + \frac{4}{14} \times 0.81 = 0.911 144×1.0+146×0.918+144×0.81=0.911
信息增益:Gain(S,temperture)=0.940−0.911=0.029Gain(S, temperture) = 0.940 - 0.911 = 0.029Gain(S,temperture)=0.940−0.911=0.029
Gain(S,Outlook)=0.247Gain(S,Humidity)=0.151Gain(S,Wind)=0.048Gain(S,Temperature)=0.029Gain(S,Outlook)=0.247 \\ Gain(S, Humidity)=0.151 \\ Gain(S, Wind)=0 .048 \\ Gain(S,Temperature)=0 .029 Gain(S,Outlook)=0.247Gain(S,Humidity)=0.151Gain(S,Wind)=0.048Gain(S,Temperature)=0.029
计算出所有的信息增益之后,选择有最大的信息增益的特征作为根节点。
下面找Sunny分支的决策树划分:
总的熵值
−25×log2(25)−35log2(35)=0.97-\frac{2}{5} \times log_2(\frac{2}{5}) - \frac{3}{5}log_2(\frac{3}{5}) = 0.97 −52×log2(52)−53log2(53)=0.97
以剩下的三个特征进行分析:
-
temperture
- temperture=hot,熵值为0,概率为25\frac{2}{5}52
- temperture=mild,熵值为1.0,概率为25\frac{2}{5}52
- temperture=cool,熵值为0,概率为15\frac{1}{5}51
熵值为25\frac{2}{5}52
信息增益:0.97−0.4=0.570.97-0.4 = 0.570.97−0.4=0.57
-
humidity
- high,熵值为0,概率为35\frac{3}{5}53
- normal,熵值为1,概率为25\frac{2}{5}52
熵值为25\frac{2}{5}52
信息增益:0.97−0.4=0.570.97 - 0.4 = 0.570.97−0.4=0.57
-
windy
- false,熵值为0.918,概率为35\frac{3}{5}53
- true,熵值为1,概率为25\frac{2}{5}52
熵值为0.9510.9510.951
信息增益:0.97−0.95=0.020.97 - 0.95 = 0.020.97−0.95=0.02
故选择humidy或temperture划分
剩下的划分同理
最终决策树:
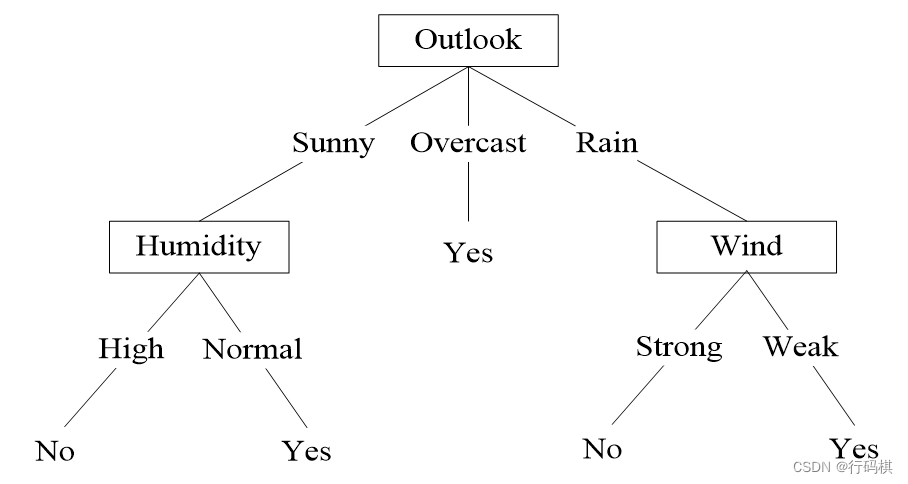
相关文章:

人工智能及其应用(蔡自兴)期末复习
人工智能及其应用(蔡自兴)期末复习 相关资料: 人工智能期末复习 人工智能复习题 人工智能模拟卷 人工智能期末练习题 1 ⭐️绪论 人工智能:人工智能就是用人工的方法在机器(计算机)上实现的智能࿰…...
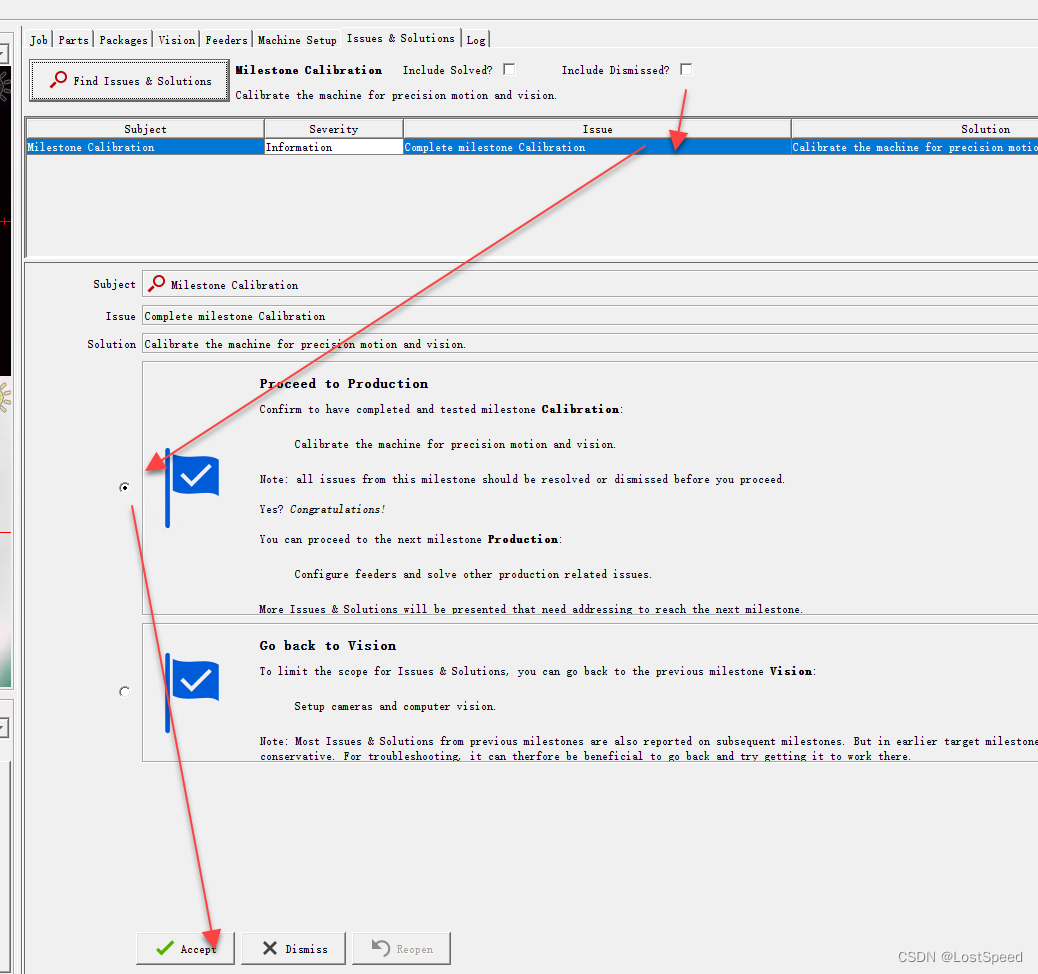
openpnp - configure - 矫正里程碑
文章目录openpnp - configure - 矫正里程碑概述备注ENDopenpnp - configure - 矫正里程碑 概述 进入矫正里程碑了 查找问题 现在第一个问题是X轴的齿隙矫正 根据提示, 将顶部相机移动到主基准点上, 选择容差(就选用默认的0.025), 开始矫正. 正好开机后, 使能了视觉原点归零. …...
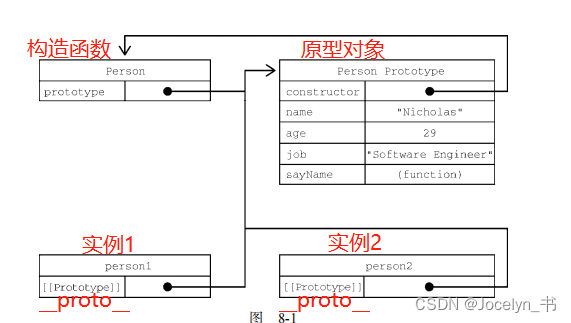
JavaScript高级程序设计读书分享之8章——8.2创建对象
JavaScript高级程序设计(第4版)读书分享笔记记录 适用于刚入门前端的同志 创建Object的实例 let person new Object(); person.name "Nicholas"; person.age 29; person.job "Software Engineer"; person.sayName function() { console.log(this…...

关于Could not build wheels for opencv-python-headless, which is...报错的解决方案
在通过最新版pip在线安装package:opencv-python-headless的时候,会产生报错信息,主要为 ERROR: Failed building wheel for opencv-python-headless ERROR: Could not build wheels for opencv-python-headless, which is required to insta…...
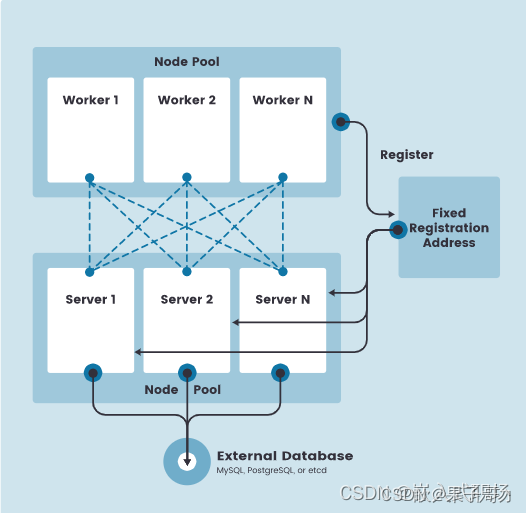
【K3s】第1篇 K3s入门级介绍及架构详解
1、什么是 K3s? K3s 是一个轻量级的 Kubernetes 发行版,它针对边缘计算、物联网等场景进行了高度优化。K3s 有以下增强功能: 打包为单个二进制文件。使用基于 sqlite3 的轻量级存储后端作为默认存储机制。同时支持使用 etcd3、MySQL 和 PostgreSQL 作…...

Java学习--反射
1. 反射 1.1 反射的概述: **专业的解释(了解一下):**是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法;对于任意一个对象,都能够调用它的任意属性和方法ÿ…...
)
应用和迭代(名词解释)
应用和迭代是什么意思 应用: ● 一个完整的前端应用,一般用应用脚手架创建,包含路由,页面,状态等 ● 一个应用对应一个代码仓库 ● 应用的分组(业务中心,数据中台等)只用于逻辑分类&…...

HTMLCollection 和 NodeList 区别
Node 和 Element DOM 是一棵树,所有节点都是 NodeNode 是 Element 的基类Element 是其他 HTML 元素的基类,如 HTMLDivElement HTMLCollection 和 NodeList HTMLCollection 是 Element 的集合NodeList 是 Node 的集合 <body><p id"p1&qu…...

fork()出来一个进程,这个进程的父进程是从哪来的?
基本概念fork() creates a new process by duplicating the calling process. The new process is referred to as the child process. The calling process is referred to as the parent process.fork()是一个系统调用,不是一个函数。详细信息可以,man…...

结构体内存对齐
结构体相信大家已经了解过了,现在我们深入讨论一个问题,计算结构体的大小 也是很热门的一个考点:结构体内存对齐 先看看下面结构体的大小 typedef struct Test {char a;char b;char c; }Test; 很容易看出答案为3,结构体的大小位…...
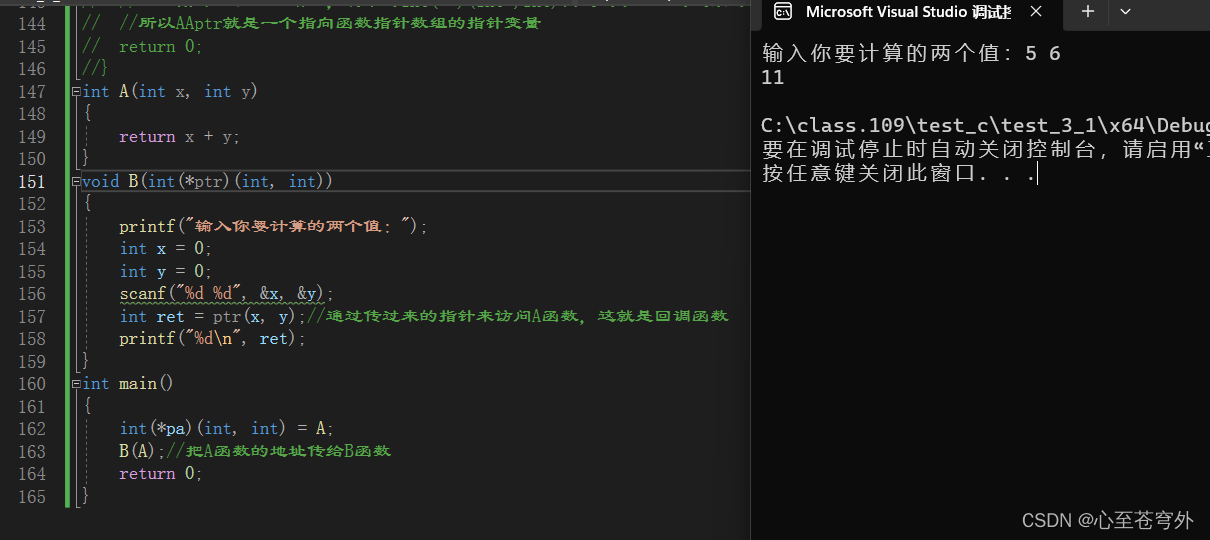
【C语言进阶】指针进阶
今日所做之事勿候明天,自我所做之事勿候他人。 --歌德 目录 指针进阶(更深层次的理解): 一.字符指针 二.指针数组 三.数组指针 1.数组指针的定义: 2.&数组名和数组名: 3.数组指针的使用: 四.数组参数,指针参数 1.一维数组传参:…...

java:Class的isPrimitive方法使用
java:Class的isPrimitive方法使用 1 前言 java中Class类的isPrimitive方法,用于检查类型是否为基本类型。java虚拟机创建了int、byte、short、long、float、double、boolean、char这8种基础信息,以及void,一共9种。为这9种类型时…...
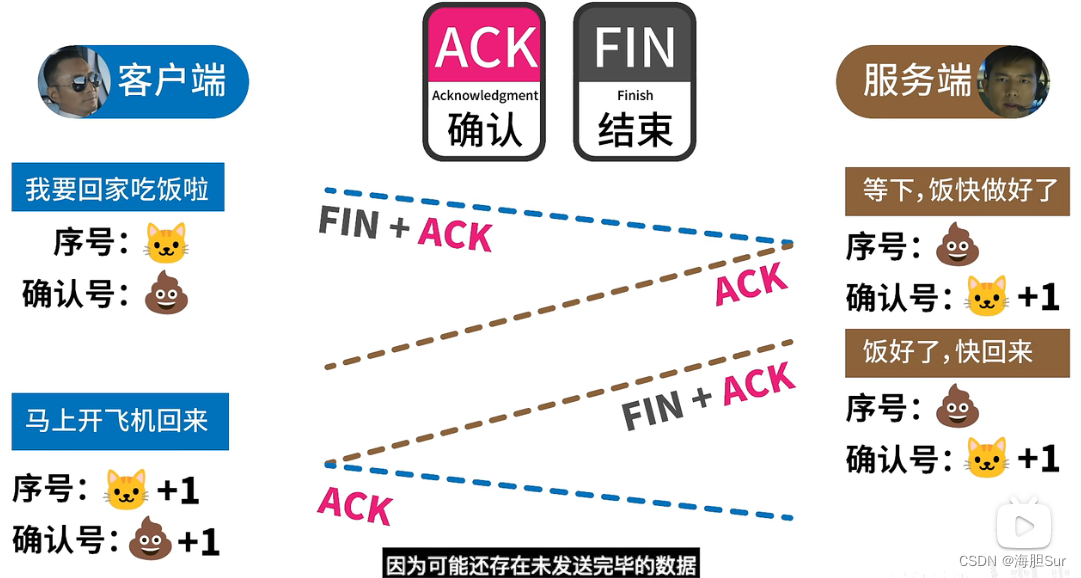
TCP 握手过程 三次 四次
蛋老师视频 SYN 同步 ACK 确认 FIN 结束 核心机制是确定哪些请求或响应需要丢弃 SYN、ACK、FIN 通过 1/0 设置开启/关闭 开启SYN后,报文中会随机生成 Sequence序号 用于校验 (应用可能发起多个会话,可以区分) 服务器的同步序…...
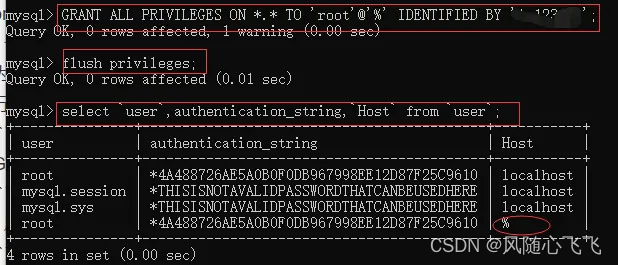
windows 下 安裝mysql 5.7.41 (64位) 超简单方式
文章目录1. 安装包下载2.安装步骤3. 服务卸载方式4. 配上 my.ini 常用配置1. 安装包下载 注意,截至2023年2月23日,MySQL所有版本不提供ARM芯片架构的Windows版本(8.0.12开始支持Red Hat系统的ARM版本),所以ARM架构的Windows无法安装MySQL&am…...
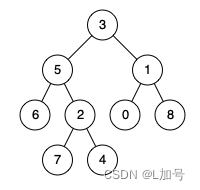
二叉树——二叉树的最近公共祖先
二叉树的最近公共祖先 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一…...
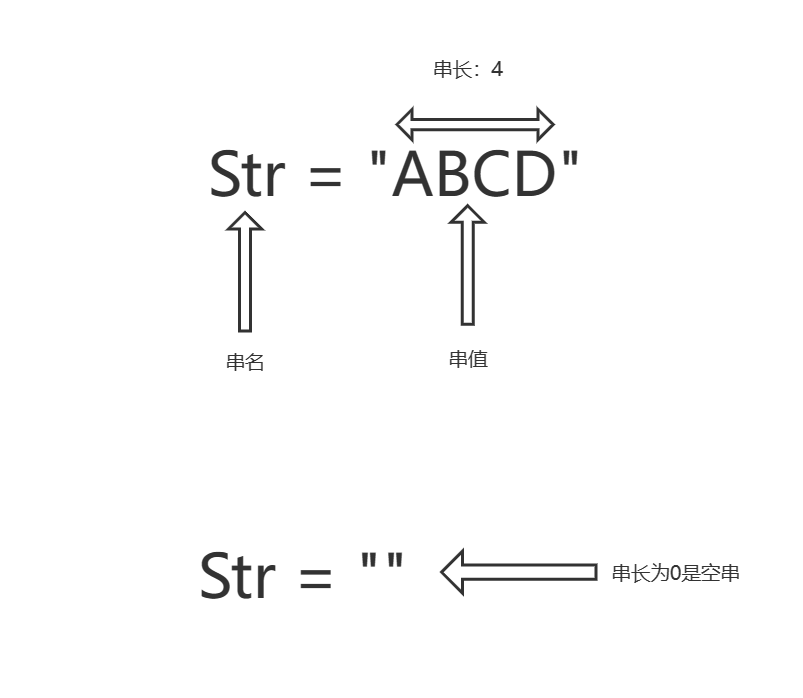
数据结构与算法基础-学习-14-线性表之串
一、串的定义由0-n个字符组成的有限序列。(n>0)二、串的相关术语1、子串串中任意个连续字符组成的子序列成为该串的子串。2、主串包含子串的串成为主串。3、字符位置字符在序列中的序号为该字符在串中的位置。4、子串位置子串第一个字符在主串中的位置…...

Mac 快捷键
目录 命令行快捷键 命令行快捷键 control d 命令行中代表发送EOF终止输入 control u 删除光标之前到行首的字符 control k 删除光标之前到行尾的字符(比较常用) control a 移动光标到行首(常用) control e 移动光标到行尾 control l 清屏,相当于clear命令 con…...

【微服务】-微服务环境搭建
目录 2.1 技术选型 2.2 模块设计 2.3 微服务调用 2.4 创建⽗⼯程 2.5 创建商品微服务 2.6 创建订单微服务 2.1 技术选型 持久层: SpingData Jpa 数据库: MySQL5.7 其他: SpringCloud Alibaba 技术栈 2.2 模块设计 --- shop-parent ⽗⼯程 --- shop-product-api 商品微服…...

IGKBoard(imx6ull)-ADC编程MQ-2烟雾传感器采样
文章目录1- ADC介绍2- MQ-2烟雾传感器介绍(1)工作原理(2)MQ-2应用电路3- MQ-2烟雾传感器硬件连接4- ADC驱动配置5- 编程查看当前浓度1- ADC介绍 ADC是Analog-to-Digital Converter的缩写,指模数转换器。真实世界的模拟…...
前端二面vue面试题总结
什么是 mixin ? Mixin 使我们能够为 Vue 组件编写可插拔和可重用的功能。如果希望在多个组件之间重用一组组件选项,例如生命周期 hook、 方法等,则可以将其编写为 mixin,并在组件中简单的引用它。然后将 mixin 的内容合并到组件中…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
