【九日集训】第九天:简单递归
递归就是自己调用自己,例如斐波那契数列就是可以用简单递归来实现。
第一题 172. 阶乘后的零
https://leetcode.cn/problems/factorial-trailing-zeroes/description/
这一题纯粹考数学推理能力,我这种菜鸡看了好久都没有懂。
大概是这样的思路:
算n!中尾随0的数量第一时间想到的是10的因子,但到n = 5就不适用了,毕竟这里还是120包含1个0呢;
仔细观察可以发现有0的尾数阶乘结果中都包含2和5,恰好2*5 = 10我们只需要找成对的2和5就可以了。
但是举一个例子:
11! = 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 11 * (2 * 5) * 9 * (4 * 2) * 7 * (3 * 2) * (1 * 5) * (2 * 2) * 3 * (1 * 2) * 1
其中含有2的因子比5的次数多,且每出现一次5就会出现一次2,所以我们这里只需要找有多少个5即可。
但仔细观察可以发现,每隔5个数字出现一个5,每隔25个数字出现两个5,每隔125个数字出现3个5,以此类推
所以只需要按顺序加下去就得到最终的结果
int trailingZeroes(int n) {if(n < 5) return 0;return n / 5 + trailingZeroes(n / 5);
}
第二题 1342. 将数字变成 0 的操作次数
https://leetcode.cn/problems/number-of-steps-to-reduce-a-number-to-zero/description/
如果是0则返回0;
如果给定的数是偶数则除以2递归到下一层,同时将操作数 + 1;
否则减2同时操作数 + 1;
int numberOfSteps(int num) {if(num == 0) return 0;if(num % 2 == 0) {return numberOfSteps(num / 2) + 1;}return numberOfSteps(num - 1) + 1;
}
第三题 222. 完全二叉树的节点个数
https://leetcode.cn/problems/count-complete-tree-nodes/description/
算二叉树的节点个数,递归节点的左子树和右子树每次递归都将结果 + 1;
如果递归到节点为空则返回0;
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
int countNodes(struct TreeNode* root) {if(root == NULL) {return 0;}return countNodes(root->left) + countNodes(root->right) + 1;
}
第四题 LCP 44. 开幕式焰火
https://leetcode.cn/problems/sZ59z6/description/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int Hash[1024];void transfer(struct TreeNode* root) {if(root) {Hash[root->val] = 1;transfer(root->left);transfer(root->right);}
}int numColor(struct TreeNode* root){int sum = 0;memset(Hash, 0, sizeof(Hash));transfer(root);for(int i = 1; i <= 1000; ++i) {if(Hash[i]) ++sum;}return sum;
}
第五题 397. 整数替换
https://leetcode.cn/problems/integer-replacement/description/
int min(int a, int b) {return a > b ? b : a;
}int integerReplacement(int n) {if(n == 1) return 0;if(n % 2 == 0) {return integerReplacement(n / 2) + 1;}return 2 + min(integerReplacement(n / 2), integerReplacement(n / 2 + 1));
}
第六题 938. 二叉搜索树的范围和
https://leetcode.cn/problems/range-sum-of-bst/description/
题目中给的是二叉搜索树,特点就是左小右大,因此如果当前root的val满足条件则将val加到return中,再加上左右子树满足条件的val和。
如果root的val大于high,则需要向左子树(小的一端)递归;
反之小于low向右子树递归;
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int rangeSumBST(struct TreeNode* root, int low, int high) {if(root == NULL) return 0;if(root->val > high) {return rangeSumBST(root->left, low, high);}if(root->val < low) {return rangeSumBST(root->right, low, high);}return root->val + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low ,high);
}
第八题 LCR 175. 计算二叉树的深度
https://leetcode.cn/problems/er-cha-shu-de-shen-du-lcof/description/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int max(int a, int b) {return a > b ? a : b;
}int calculateDepth(struct TreeNode* root) {if(root == NULL) return 0;return max(calculateDepth(root->left), calculateDepth(root->right)) + 1;
}
第九题 104. 二叉树的最大深度
这一题和上一题一样
https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int max(int a, int b) {return a > b ? a : b;
}int maxDepth(struct TreeNode* root) {if(root == NULL) return 0;return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
第十题 226. 翻转二叉树
https://leetcode.cn/problems/invert-binary-tree/description/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
struct TreeNode* invertTree(struct TreeNode* root) {if(root == NULL) return NULL;struct TreeNode* left = invertTree(root->left);struct TreeNode* right = invertTree(root->right);root->left = right;root->right = left;return root;
}
相关文章:

【九日集训】第九天:简单递归
递归就是自己调用自己,例如斐波那契数列就是可以用简单递归来实现。 第一题 172. 阶乘后的零 https://leetcode.cn/problems/factorial-trailing-zeroes/description/ 这一题纯粹考数学推理能力,我这种菜鸡看了好久都没有懂。 大概是这样的思路&#x…...
Prime 1.0
信息收集 存活主机探测 arp-scan -l 或者利用nmap nmap -sT --min-rate 10000 192.168.217.133 -oA ./hosts 可以看到存活主机IP地址为:192.168.217.134 端口探测 nmap -sT -p- 192.168.217.134 -oA ./ports UDP端口探测 详细服务等信息探测 开放端口22&#x…...

Java 如何正确比较两个浮点数
看下面这段代码,将 d1 和 d2 两个浮点数进行比较,输出的结果会是什么? double d1 .1 * 3; double d2 .3; System.out.println(d1 d2);按照正常逻辑来看,d1 经过计算之后的结果应该是 0.3,最后打印的结果应该是 tru…...
Qt 如何操作SQLite3数据库?数据库创建和表格的增删改查?
# 前言 项目源码下载 https://gitcode.com/m0_45463480/QSQLite3/tree/main # 第一步 项目配置 平台:windows10 Qt版本:Qt 5.14.2 在.pro添加 QT += sql 需要的头文件 #include <QSqlDatabase>#include <QSqlError>#include <QSqlQuery>#include &…...
【Hadoop】分布式文件系统 HDFS
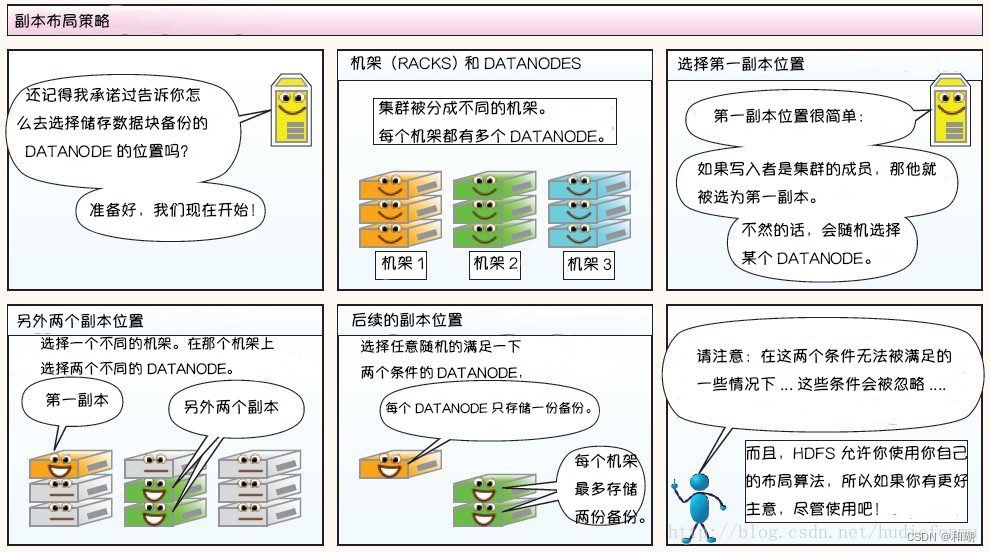
目录 一、介绍二、HDFS设计原理2.1 HDFS 架构2.2 数据复制复制的实现原理 三、HDFS的特点四、图解HDFS存储原理1. 写过程2. 读过程3. HDFS故障类型和其检测方法故障类型和其检测方法读写故障的处理DataNode 故障处理副本布局策略 一、介绍 HDFS (Hadoop Distribute…...

【Python-随笔】使用Python实现屏幕截图
使用Python实现屏幕截图 环境配置 下载pyautogui包 pip install pyautogui -i https://pypi.tuna.tsinghua.edu.cn/simple/下载OpenCV包 pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple/下载PyQT5包 pip install PyQt5 -i https://pypi.tuna.tsi…...

Sun Apr 16 00:00:00 CST 2023格式转换
Date date new Date(); log.info("当前时间为:{}",date); //yyyy-MM-dd HH:mm:ss SimpleDateFormat sdf new SimpleDateFormat(DateUtils.YYYY_MM_DD_HH_MM_SS); String dateTime s…...

使用mongodb实现简单的读写操作
本文适合初学者,特别是刚刚安装了mongodb数据库的朋友,或在atlas刚拿到免费集群的朋友。 拿到数据库,心情很激动,手痒难耐。特别想向数据库插入几条数据库试试。即使是深夜完成了安装,也忍不住想去完成这些操作。看到…...

C语言实现Cohen_Sutherland算法
前提简要: 算法简介: 编码算法是最早、最流行的线段裁剪算法,该算法采用区域检验的方法,能够快速有效地判断一条线段与裁剪窗口的位置关系,对完全接受或完全舍弃的线段无需求交,即可直接识别。 算法思想&…...

MySQL进阶_EXPLAIN重点字段解析
文章目录 第一节.准备1.1 版本信息1.2 准备 第二节.type2.1 system2.2 const2.3 eq_ref2.4 ref2.5 ref_or_null2.6 index_merge2.7 unique_subquery2.8 range2.9 index2.10 all 第三节. Extra3.1 No tables used3.2 No tables used3.3 Using where3.4 No matching min/max row3…...
视图层与模板层
视图层 1 视图函数 一个视图函数,简称视图,是一个简单的Python 函数,它接受Web请求并且返回Web响应。响应可以是一张网页的HTML内容,一个重定向,一个404错误,一个XML文档,或者一张图片. . . 是…...
)
MySQL数据库——触发器-案例(Insert类型、Update类型和Delete类型)
目录 表结构准备 插入数据触发器 代码 测试 修改数据触发器 代码 测试 删除数据触发器 代码 测试 通过触发器记录 tb_user 表的数据变更日志,将变更日志插入到日志表user_logs中,包含增加,修改,删除。 表结构准备 根据…...
)
快速创建桌面端(electron-egg)
介绍 | electron-egg electron-egg: 一个入门简单、跨平台、企业级桌面软件开发框架。 electron-egg是一个基于Electron和Egg.js的框架,可以用于快速构建跨平台的桌面应用程序。 1.兼容平台:electron-egg可以在Windows、MacOS和Linux等多个平台上运行…...

docker配置redis插件
docker配置redis插件 运行容器redis_6390 docker run -it \ --name redis_6390 \ --privileged \ -p 6390:6379 \ --network wn_docker_net \ --ip 172.18.12.19 \ --sysctl net.core.somaxconn1024 \ -e TIME_ZONE"Asia/Shanghai" -e TZ"Asia/Shanghai"…...
前端入口教程_web01
web标准 记得看! html:表示整个页面 head: titile: body: 常用标签 1.标题标签 2.段落标签 3.换行标签 4.文本格式化标签 5. 和 标签 6.图像标签 相对路径–用来插自己本地的图片 #### 绝对路径–用来插网上找的图…...
Win7 SP1 x64 Google Chrome 字体模糊
1 打开 Google Chrome ,地址栏输入 chrome://version/ ,字体模糊。 2 Microsoft Update Catalog 搜索更新 kb2670838,下载,安装,重启电脑。 3 打开 Google Chrome,地址栏输入 chrome://version/ ࿰…...
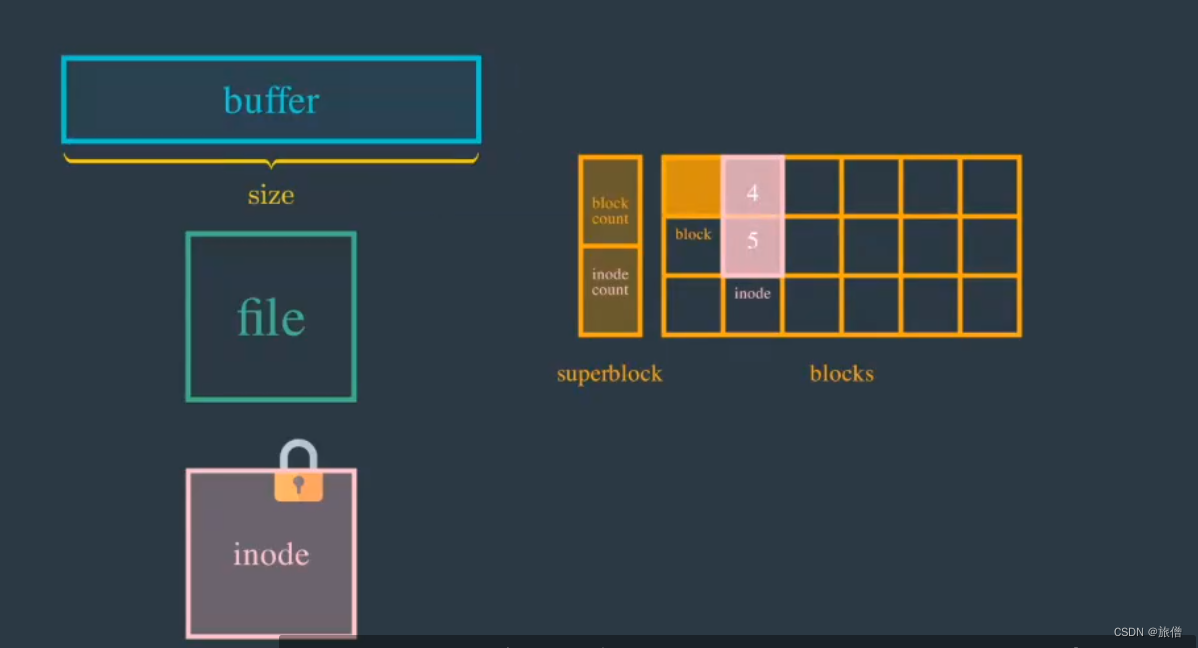
read()之后操作系统都干了什么
首先说明三个参数 file文件 buff从内存中开辟一段缓冲区用来接收读取的数据 size表示这个缓冲区的大小 有关file的参数: 状态:被打开 被关闭权限:可读可写最重要的是inode: 他包含了 文件的元数据(比如文件大小 文件类型 文件在访问前需要加…...
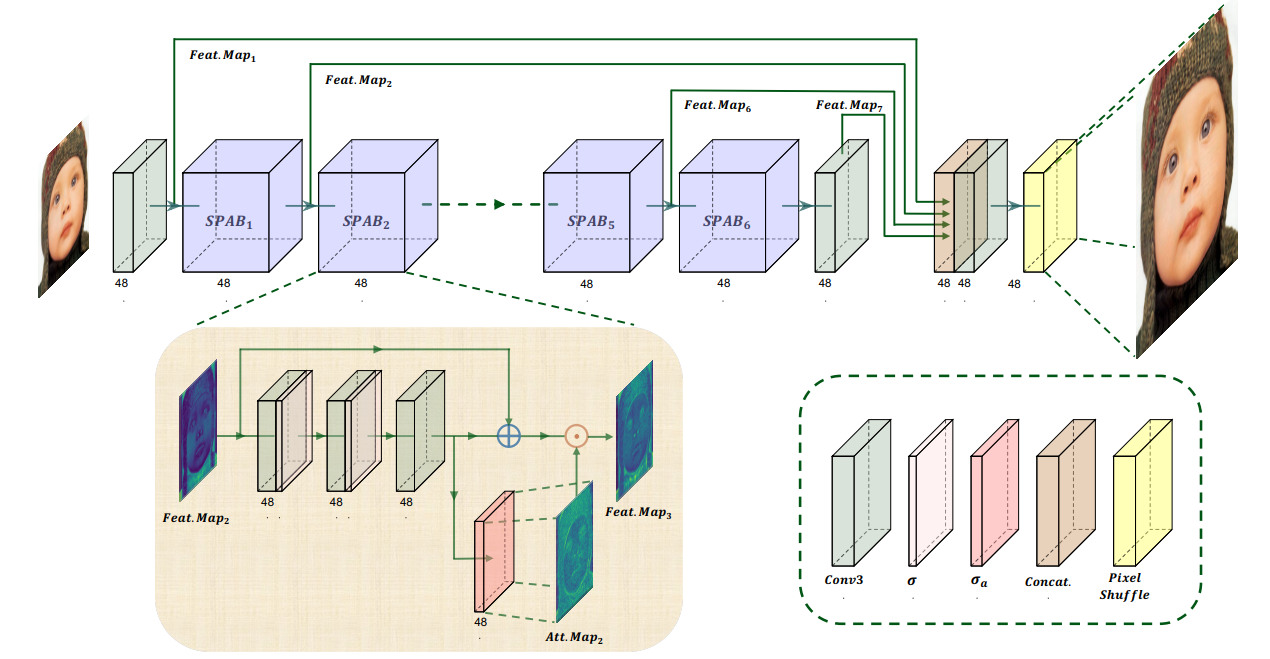
YoloV8改进策略:Swift Parameter-free Attention,无参注意力机制,超分模型的完美迁移
摘要 https://arxiv.org/pdf/2311.12770.pdf https://github.com/hongyuanyu/SPAN SPAN是一种超分网络模型。SPAN模型通过使用参数自由的注意力机制来提高SISR的性能。这种注意力机制能够增强重要信息并减少冗余,从而在图像超分辨率过程中提高图像质量。 具体来说,SPAN模…...

Python----练习:使用面向对象实现报名系统开发
第一步:分析哪些动作是由哪些实体发出的 学生提出报名 学生提供相关资料 学生缴费 机构收费 教师分配教室 班级增加学生信息 于是,在整个过程中,一共有四个实体:学生、机构、教师、班级!在现实中的一个具体的实…...

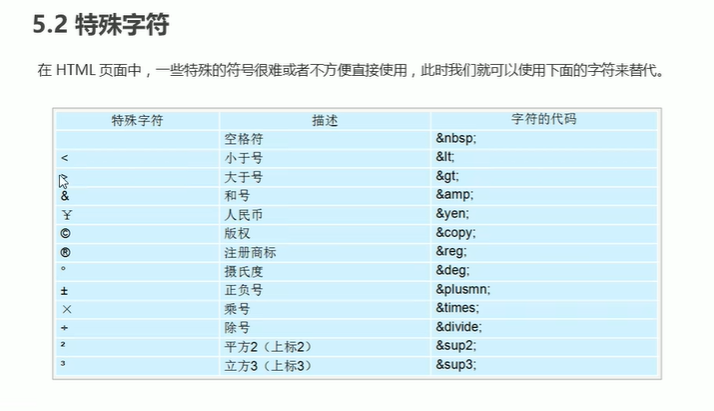
1.什么是html
1.什么是html什么是html? 一.基础信息 英文名字:HyperText Markup Language 中文名字:超文本标记语言 简称:html 文件格式:.htm 或 .html 结尾 作用:描述网页的语言。通过各种各样的标签,组…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
