L1-017:到底有多二
题目描述
一个整数“犯二的程度”定义为该数字中包含2的个数与其位数的比值。如果这个数是负数,则程度增加0.5倍;如果还是个偶数,则再增加1倍。例如数字
-13142223336是个11位数,其中有3个2,并且是负数,也是偶数,则它的犯二程度计算为:3/11×1.5×2×100%,约为81.82%。本题就请你计算一个给定整数到底有多二。
输入格式:
输入第一行给出一个不超过50位的整数
N。
输出格式:
在一行中输出
N犯二的程度,保留小数点后两位。
输入样例:
-13142223336输出样例:
81.82%
分析
因为输入的数是不超过50位的,因此要借助字符数组来存储这个整数N。
程序代码
#include<stdio.h>
#include<string.h>
int main(){char a[50];double t;int count=0;scanf("%s",a);int x=strlen(a);//测量该整数的位数for(int i=0;i<x;i++){//找出这个整数有几个2if(a[i]=='2'){count++;}}if(a[0]=='-'){//判断是否为负数t=(double)count/(x-1)*1.5;if((a[x-1]-'0')%2==0)//判断是否为偶数t=t*2;}else{t=(double)count/x;if((a[x-1]-'0')%2==0)t=t*2;
}printf("%.2lf%%",t*100);//输出相应的结果return 0;
}运行结果

相关文章:

L1-017:到底有多二
题目描述 一个整数“犯二的程度”定义为该数字中包含2的个数与其位数的比值。如果这个数是负数,则程度增加0.5倍;如果还是个偶数,则再增加1倍。例如数字-13142223336是个11位数,其中有3个2,并且是负数,也是…...
)
Python多线程使用(二)
使用多个线程的时候容易遇到一个场景:多个线程处理一份数据 使用多线程的时候同时处理一份数据,在threading中提供了一个方法:线程锁 Demo:下订单 现在有多笔订单下单,库存减少 from threading import Thread from t…...

记录一次docker搭建tomcat容器的网页不能访问的问题
tomcat Tomcat是Apache软件基金会的Jakarta项目中的一个重要子项目,是一个Web服务器,也是Java应用服务器,是开源免费的软件。它是一个兼容Java Servlet和JavaServer Pages(JSP)的Web服务器,可以作为独立的W…...

GPT3年终总结
User You 程序员年度绩效总结 ChatGPT ChatGPT 程序员年度绩效总结通常包括以下几个方面: 目标达成情况: 回顾年初设定的目标,评估在项目完成、技能提升等方面的达成情况。 工作贡献: 强调在项目中的个人贡献,包括…...

Kafka生产者发送消息的流程
Kafka 生产者发送消息的流程涉及多个步骤,从消息的创建到成功存储在 Kafka 集群中。以下是 Kafka 生产者发送消息的主要步骤: 1. 创建消息 生产者首先创建一个消息,消息通常包含一个键(可选)和一个值,以及…...
基于SSM的数学竞赛网站设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

01-使用Git操作本地库,如初始化本地库,提交工作区文件到暂存区和本地库,查看版本信息,版本切换命令等
Git的使用 概述 Git是一个分布式版本控制工具, 通常用来管理项目中的源代码文件(Java类、xml文件、html页面等)进行管理,在软件开发过程中被广泛使用 Git可以记录文件修改的历史记录并形成备份从而实现代码回溯, 版本切换, 多人协作, 远程备份的功能Git具有廉价的本地库,方便…...
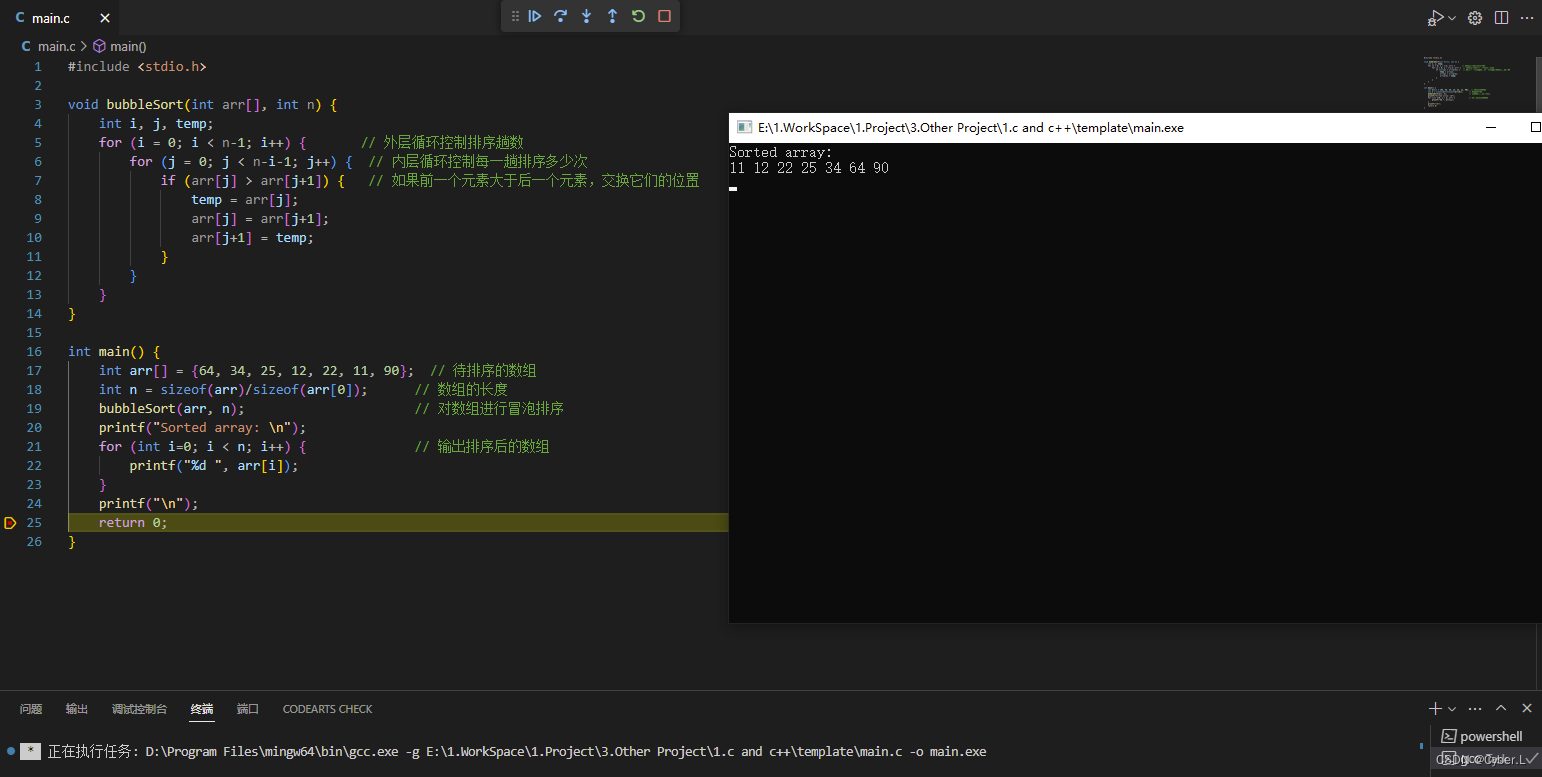
排序算法介绍(二)冒泡排序
0. 简介 冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排…...

搜索引擎高级用法总结: 谷歌、百度、必应
搜索引擎高级用法总结: 谷歌、百度、必应 google search 基本搜索 逻辑与:and逻辑或: or逻辑非: -完整匹配:“关键词”通配符:* ?高级搜索 intext:后台登录 将只返回正文中包含 后台登录 的网页 intitle intitle:后台登录 将只返回标题中包含 后台登录 的网页,intitle…...

com.intellij.openapi.application.ApplicationListener使用
一般监听期通过如下代码生效 <applicationListeners> <!-- <listener class"com.itheima.taunt.MyApplicationListener"--> <!-- topic"com.intellij.openapi.application.ApplicationListener"…...

常见js hook脚本
一.js hook 过无限debugger var _constructor constructor; Function.prototype.constructor function(s) {if (s "debugger") {console.log(s);return null;}return _constructor(s); }//去除无限debugger Function.prototype.__constructor_back Function.pro…...

Java——SpringLayout弹簧布局
import java.awt.*;import javax.swing.*;public class a {public static void main(String[] args) {new a();}public a() {JFrame JF new JFrame("弹簧布局");// 创建JFrame窗口//设置JPanel的布局管理器为SpringLayoutJPanel JP new JPanel(new SpringLayout())…...
正则表达式及文本三剑客grep sed awk
目录 正则表达式 1.元字符 2.表示次数 3.位置锚定 4.分组或其他 grep sed 语法: 常用选项 脚本格式 例: 查找11点56到12点10的日志 修改文件,找到文件并给其后缀加上er 提取IP地址 提取版本号 提取文件权限 awk 工作原理&…...

python爬虫之创建属于自己的ip代理池
在后续需求数据量比较大的情况下,自建一个ip代理池可以帮助我们获得更多的数据。 下面我来介绍一下整个过程 1.找到目标代理网站 https://www.dailiservers.com/go/webshare https://proxyscrape.com/ https://spys.one/ https://free-proxy-list.net/ http://fr…...

又添三位“信伙伴”,亚信安慧AntDB数据库与南京一鸣、广东鸿数、北京数见完成兼容互认
近日,亚信安慧AntDB数据库与南京一鸣科技有限公司(简称:南京一鸣)学生工作管理与服务平台软件、广东鸿数科技有限公司(简称:广东鸿数)隐私数据保护系统V5.0、北京数见科技有限公司(简…...
Linux --- 进程控制
目录 1. 进程创建 1.1. 内核数据结构的处理 1.2. 代码的处理 1.3. 数据的处理: 方案一:fork创建子进程的时候,直接对数据进行拷贝处理,让父子进程各自私有一份 方案二:写实拷贝(copy on write) 1.4. fork常规用…...

SVG-椭圆弧-参数转换-计算公式-标准解读
文章目录 1.简介2.基本参数2.1.椭圆的表达2.2.参数变换2.3.注意事项 3.参考资料4.总结 1.简介 为了与其他路径段表示法保持一致, SVG 路径中的圆弧是根据曲线上的起点和终点定义的。椭圆弧的这种端点参数化。优点是它允许与其它路径一致的语法,其中所有…...

利用 LD_PRELOAD劫持动态链接库,绕过 disable_function
目录 LD_PRELOAD 简介 程序的链接 动态链接库的搜索路径搜索的先后顺序: 利用LD_PRELOAD 简单的劫持 执行id命令 反弹shell 引申至 PHP 绕过disable_function 方法1:使用蚁剑的扩展工具绕过disable_function 方法2:利用 mail 函数…...
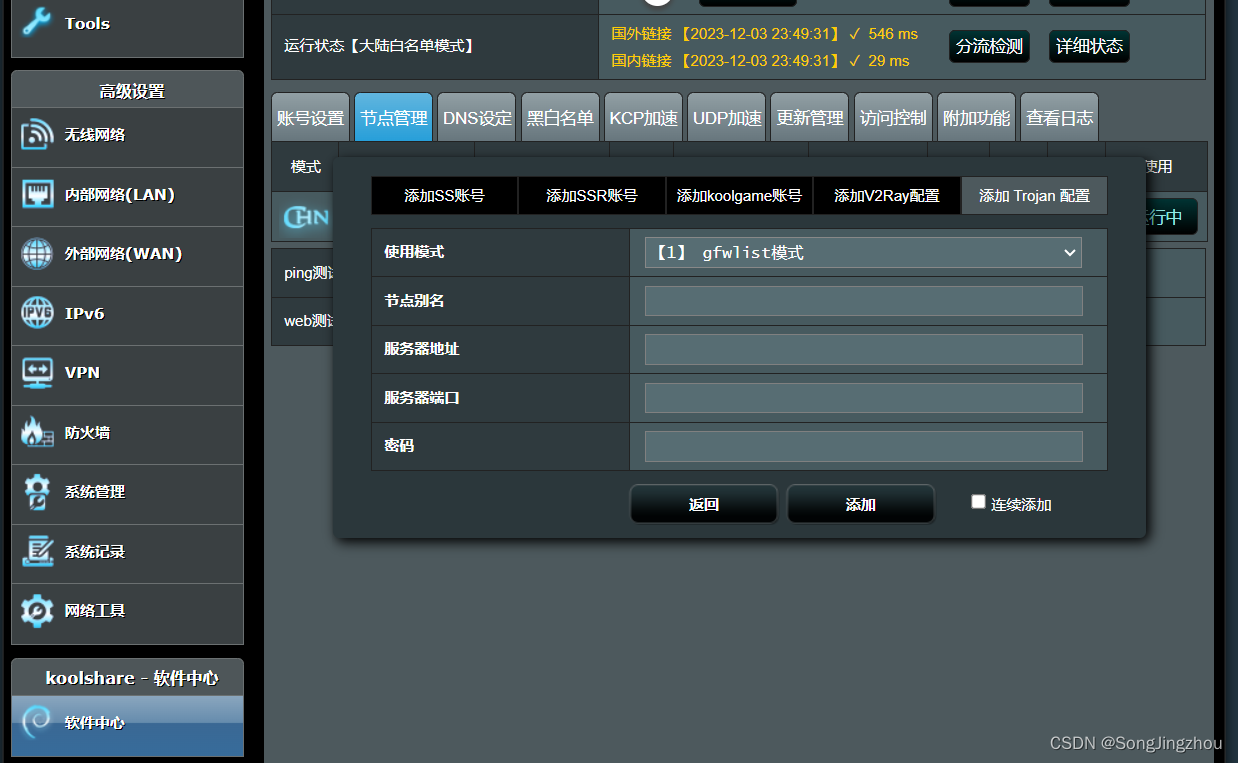
网件R8500 trojan
一 将路由器刷机成改版梅林 路由器首页的Firmware:380.70_0-X7.9.1是梅林改版 380.xx 梅林原版固件 380.xx_x 梅林改版固件 必须是改版梅林才支持trojan,所以要确保是梅林改版固件 点击上传文件,选择下载好的改版固件,固件地址下载传送门…...

实现校园网开机自启动部署
❤️博客主页: iknow181🔥系列专栏: Python、JavaSE、JavaWeb、CCNP🎉欢迎大家点赞👍收藏⭐评论✍ 目录 一.准备工作 1、IDE安装 2、安装Selenium 1.介绍 2.下载 3、安装pywifi 1.介绍 2.下载 4、下载浏览器驱…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...
