详解—[C++数据结构]—红黑树
目录
一、红黑树的概念
编辑二、红黑树的性质
三、红黑树节点的定义
四、红黑树结构
五、红黑树的插入操作
5.1. 按照二叉搜索的树规则插入新节点
5.2、检测新节点插入后,红黑树的性质是否造到破坏
情况一: cur为红,p为红,g为黑,u存在且为红
情况二: cur为红,p为红,g为黑,u不存在/u为黑
情况三: cur为红,p为红,g为黑,u不存在/u为黑
六、红黑树的验证
七、红黑树与AVL树的比较
八、key结构红黑树整体代码
九、key,value 结构红黑树整体代码
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
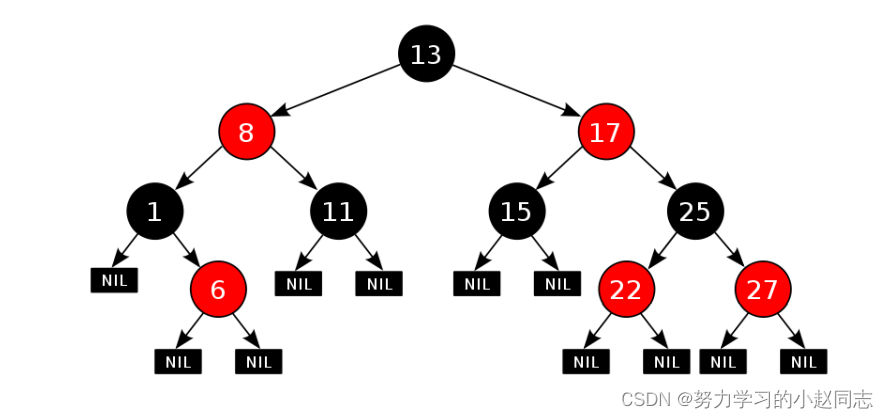 二、红黑树的性质
二、红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
三、红黑树节点的定义
红黑树的节点,我们这里使用的是三叉链,方便对后面内容的操作
首先,我们定义了一个枚举常量,来表示红黑树节点的颜色
其次,定义节点,一个红黑树的节点包含<左孩子,右孩子,父节点,数据,颜色>
接着我们定义构造函数<对其节点数据进行初始化>,左右孩子和父节点置空,插入的颜色默认为红色,数据为传入的数据。
enum COLOR
{BLACK,RED
};
template <class T>
struct RBNode
{RBNode<T>* _left;RBNode<T>* _right;RBNode<T>* _parent;T _value;COLOR _color;//颜色RBNode(const T & value=T()):_left(nullptr), _right(nullptr), _parent(nullptr), _value(value), _color(RED){}
};四、红黑树结构
为了后续封装map和set简单一些,在红黑树的实现中增加一个头结点,因为根节点必须为黑色,为了与根节点进行区分,将头结点给成黑色,并且让头结点的 pParent 域指向红黑树的根节点,pLeft域指向红黑树中最小的节点,_pRight域指向红黑树中最大的节点,如下:

五、红黑树的插入操作
相比于AVL树,插入比较简单,效率比较高,红黑树比AVL树的调整次数要少。
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
1. 按照二叉搜索的树规则插入新节点
2.检测新节点插入后,红黑树的性质是否造到破坏(有破坏进行调整)
5.1. 按照二叉搜索的树规则插入新节点
bool Insert(const T& value){// 1. 按照二叉搜索的树方式插入新节点//搜索树的插入if (_header->_parent == nullptr){//空树,创建根节点pNode root = new Node(value);root->_color = BLACK;root->_parent = _header;_header->_parent = root;_header->_left = root;_header->_right = root;return true;}//从根开始搜索pNode cur = _header->_parent;pNode parent = nullptr;//查找插入的位置while (cur){parent = cur;//按照key值确定位置, key不能重复if (cur->_value == value)return false;else if (cur->_value > value)cur = cur->_left;elsecur = cur->_right;}//节点创建cur = new Node(value);//节点插入if (parent->_value > cur->_value)parent->_left = cur;elseparent->_right = cur;//节点连接cur->_parent = parent;//while()// {// 2. 检测新节点插入后,红黑树的性质是否造到破坏,// 若满足直接退出,否则对红黑树进行旋转着色处理//}// 根节点的颜色可能被修改,将其改回黑色_header->_parent->_color = BLACK;//更新 _header->_left, _header->_right_header->_left = leftMost();_header->_right = rightMost();return true;}5.2、检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
情况一: cur为红,p为红,g为黑,u存在且为红
注意::此时看到的树,又可能是一颗完整的树,也有可能是一颗子树

如果g是根节点,调整完成后,需要把根节点改为黑色
如果g是子树,g一定有双亲(父亲和叔叔),如果g的双亲为红色,则继续往上调整
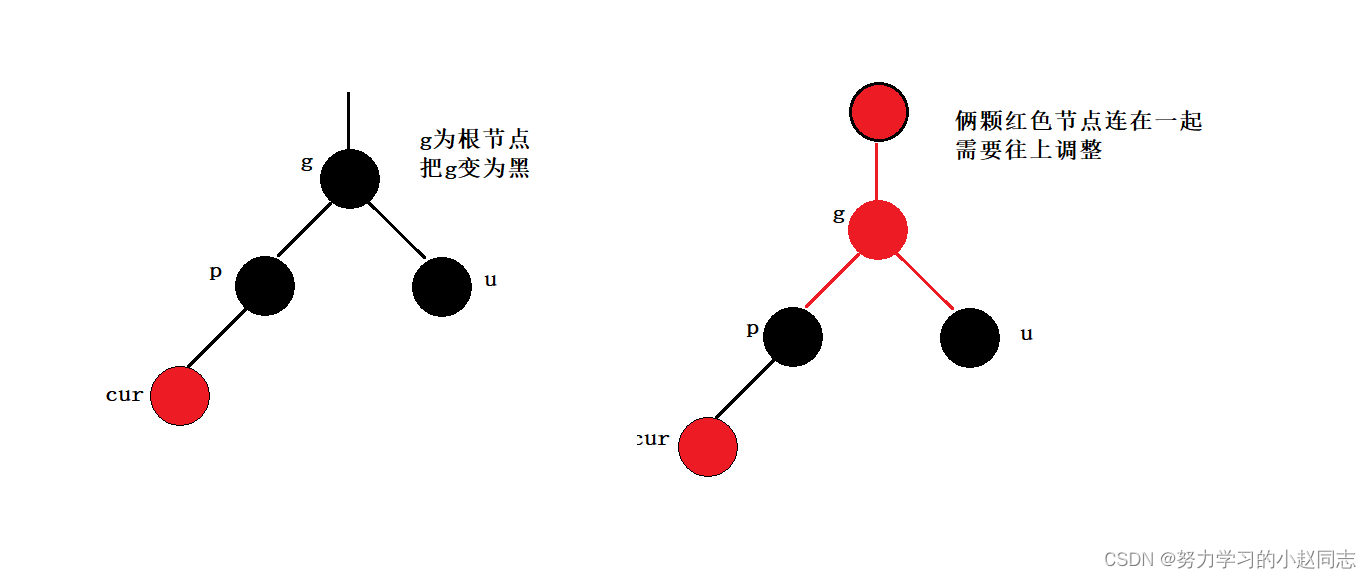
解决方式:将p,u改为黑,g改为红,然后把g当作cur,继续往上调整,直至cur为根节点(根为黑)
情况二: cur为红,p为红,g为黑,u不存在/u为黑
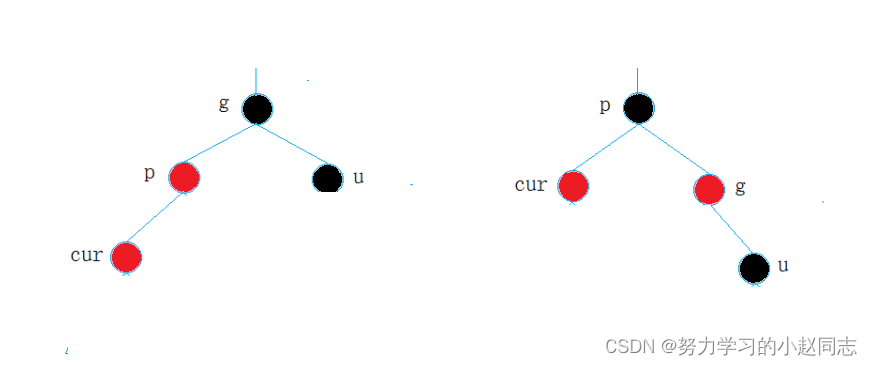
说明:
U有俩种情况:
1.如果U节点不存在,则cur一定是新插入的节点,因为如果cur不为新插入的节点,则cur和p一定有一个节点的颜色为黑色,就不满足性质4:每条路径黑色节点相同
2.如果U节点存在,则其一定是黑色的,那么cue节点原来的颜色一定是黑色的,现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改为红色。
解决方式:p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色--p变黑,g变红
情况三: cur为红,p为红,g为黑,u不存在/u为黑
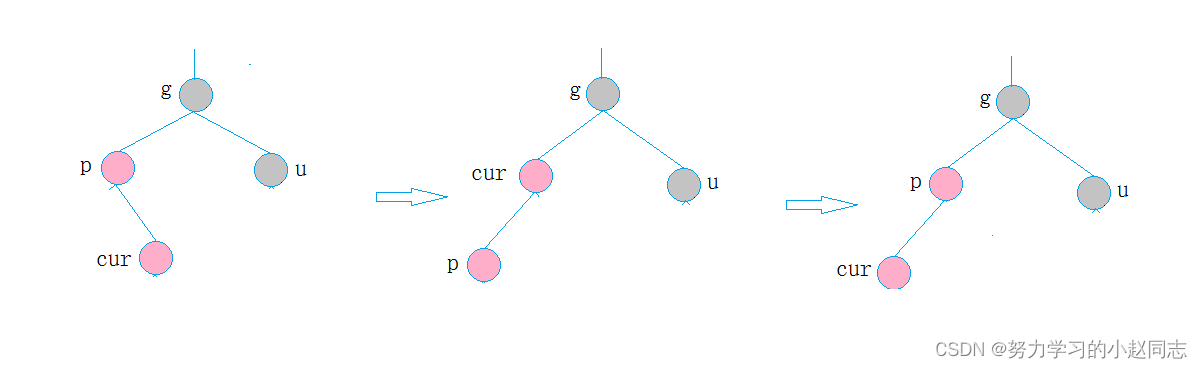
解决方式:p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
则转换成了情况2
bool insert(const T& value){//搜索树的插入if (_header->_parent == nullptr){//空树,创建根节点pNode root = new Node(value);root->_color = BLACK;root->_parent = _header;_header->_parent = root;_header->_left = root;_header->_right = root;return true;}//从根开始搜索pNode cur = _header->_parent;pNode parent = nullptr;//查找插入的位置while (cur){parent = cur;//按照key值确定位置, key不能重复if (cur->_value == value)return false;else if (cur->_value > value)cur = cur->_left;elsecur = cur->_right;}//节点创建cur = new Node(value);//节点插入if (parent->_value > cur->_value)parent->_left = cur;elseparent->_right = cur;//节点连接cur->_parent = parent;//调整和更新(颜色):连续红色需要调整while (cur != _header->_parent && cur->_parent->_color == RED)//当前不是根,并且你的父亲是红色{//cur:当前节点,parent:父亲节点, gfather:祖父节点,uncle:叔叔节点parent = cur->_parent;pNode gfather = parent->_parent;if (gfather->_left == parent){pNode uncle = gfather->_right;//uncle 存在且为红if (uncle && uncle->_color == RED){//修改颜色parent->_color = uncle->_color = BLACK;gfather->_color = RED;//继续向上更新cur = gfather;}else{//如果存在双旋的场景,可以先进行一次单旋,使它变成单旋的场景if (cur == parent->_right){RotateL(parent);swap(cur, parent);}//右旋RotateR(gfather);//修改颜色parent->_color = BLACK;gfather->_color = RED;//停止调整break;}}//gfather->_right == parentelse{pNode uncle = gfather->_left;if (uncle && uncle->_color == RED){//修改颜色uncle->_color = parent->_color = BLACK;gfather->_color = RED;cur = gfather;}else{//判断是否有双旋的场景if (cur == parent->_left){//以parent右旋RotateR(parent);//交换指针swap(cur, parent);}//以gfather 左旋RotateL(gfather);//修改颜色parent->_color = BLACK;gfather->_color = RED;//停止调整break;}}}//根的颜色始终是黑的 根:_header->_parent_header->_parent->_color = BLACK;//更新 _header->_left, _header->_right_header->_left = leftMost();_header->_right = rightMost();return true;}六、红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
2. 检测其是否满足红黑树的性质
bool isRBTree(){pNode root = _header->_parent;if (root == nullptr)return true;if (root->_color == RED){cout << "根节点必须是黑色的!!!" << endl;return false;}//根节点是黑色//需要判断每条路径上黑色个数相同//可以先任意遍历一条路径 比如走最右路径。查找black数量pNode cur = root;int blackCount = 0;while (cur){if (cur->_color == BLACK)++blackCount;cur = cur->_right;}int k = 0;return _isRBTree(root, k, blackCount);}bool _isRBTree(pNode root, int curBlackCount, int totalBlackCout)//curBlackCount:走到当前节点黑色个数{//每条路径上黑色个数相同//没有连续红色结点//一条路径走完if (root == nullptr){if (curBlackCount != totalBlackCout){cout << "每条路径-黑色结点个数不同" << endl;return false;}return true;}if (root->_color == BLACK)++curBlackCount;//没有红色连续pNode parent = root->_parent;if (parent->_color == RED && root->_color == RED){cout << "有连续的红色结点" << endl;return false;}return _isRBTree(root->_left, curBlackCount, totalBlackCout) && _isRBTree(root->_right, curBlackCount, totalBlackCout);}七、红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( ),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
八、key结构红黑树整体代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<time.h>
#include<utility>
#include<iostream>
using namespace std;
enum COLOR
{BLACK,RED
};
template <class T>
struct RBNode
{RBNode<T>* _left;RBNode<T>* _right;RBNode<T>* _parent;T _value;COLOR _color;//颜色RBNode(const T & value=T()):_left(nullptr), _right(nullptr), _parent(nullptr), _value(value), _color(RED){}
};template <class T>
class RBTree
{
public:typedef RBNode<T> Node;typedef Node* pNode;RBTree(){//构建空的红黑树 空树--》带头的红黑树,头不是根_header = new Node;_header->_left = _header;_header->_right = _header;}/*红黑树插入:1.相对于AVL树,插入比较简单,且效率高,红黑树比AVL树调整次数要少2.二叉树进行插入3.判断有没有连续的红色结点如果有:a:只需要修改颜色: uncle为红色b:修改颜色,旋转:u不存在、存在且为黑单旋:cur,parent在gfather的同一边双旋:cur,parent不在gfather的同一边,首先经过一次单璇,交换指针,转化为上面单璇场景,没有:不需要做任何操作,插入结束。*/bool insert(const T& value){//搜索树的插入if (_header->_parent == nullptr){//空树,创建根节点pNode root = new Node(value);root->_color = BLACK;root->_parent = _header;_header->_parent = root;_header->_left = root;_header->_right = root;return true;}//从根开始搜索pNode cur = _header->_parent;pNode parent = nullptr;//查找插入的位置while (cur){parent = cur;//按照key值确定位置, key不能重复if (cur->_value == value)return false;else if (cur->_value > value)cur = cur->_left;elsecur = cur->_right;}//节点创建cur = new Node(value);//节点插入if (parent->_value > cur->_value)parent->_left = cur;elseparent->_right = cur;//节点连接cur->_parent = parent;//调整和更新(颜色):连续红色需要调整while (cur != _header->_parent && cur->_parent->_color == RED)//当前不是根,并且你的父亲是红色{//cur:当前节点,parent:父亲节点, gfather:祖父节点,uncle:叔叔节点parent = cur->_parent;pNode gfather = parent->_parent;if (gfather->_left == parent){pNode uncle = gfather->_right;//uncle 存在且为红if (uncle && uncle->_color == RED){//修改颜色parent->_color = uncle->_color = BLACK;gfather->_color = RED;//继续向上更新cur = gfather;}else{//如果存在双旋的场景,可以先进行一次单旋,使它变成单旋的场景if (cur == parent->_right){RotateL(parent);swap(cur, parent);}//右旋RotateR(gfather);//修改颜色parent->_color = BLACK;gfather->_color = RED;//停止调整break;}}//gfather->_right == parentelse{pNode uncle = gfather->_left;if (uncle && uncle->_color == RED){//修改颜色uncle->_color = parent->_color = BLACK;gfather->_color = RED;cur = gfather;}else{//判断是否有双旋的场景if (cur == parent->_left){//以parent右旋RotateR(parent);//交换指针swap(cur, parent);}//以gfather 左旋RotateL(gfather);//修改颜色parent->_color = BLACK;gfather->_color = RED;//停止调整break;}}}//根的颜色始终是黑的 根:_header->_parent_header->_parent->_color = BLACK;//更新 _header->_left, _header->_right_header->_left = leftMost();_header->_right = rightMost();return true;}pNode leftMost(){pNode cur = _header->_parent;while (cur && cur->_left != nullptr){cur = cur->_left;}return cur;}pNode rightMost(){pNode cur = _header->_parent;while (cur && cur->_right != nullptr){cur = cur->_right;}return cur;}void RotateR(pNode parent){pNode subL = parent->_left;pNode subLR = subL->_right;// 1subL->_right = parent;// 2parent->_left = subLR;// 3if (subLR)subLR->_parent = parent;// 4, 5if (parent != _header->_parent){// subL <---> parent->parentpNode gParent = parent->_parent;if (gParent->_left == parent)gParent->_left = subL;elsegParent->_right = subL;subL->_parent = gParent;}else{//更新根节点_header->_parent = subL;//subL->_parent = nullptr;subL->_parent = _header;}// 6parent->_parent = subL;}void RotateL(pNode parent){pNode subR = parent->_right;pNode subRL = subR->_left;subR->_left = parent;parent->_right = subRL;if (subRL)subRL->_parent = parent;if (parent != _header->_parent) {pNode gParent = parent->_parent;if (gParent->_left == parent)gParent->_left = subR;elsegParent->_right = subR;subR->_parent = gParent;}else{_header->_parent = subR;//根的父节点不是nullptr//subR->_parent = nullptr;subR->_parent = _header;}parent->_parent = subR;}void inOrder(){_inOrder(_header->_parent);}void _inOrder(pNode root){if (root) {_inOrder(root->_left);cout << root->_value<<endl;_inOrder(root->_right);}}bool isRBTree(){pNode root = _header->_parent;if (root == nullptr)return true;if (root->_color == RED){cout << "根节点必须是黑色的!!!" << endl;return false;}//根节点是黑色//需要判断每条路径上黑色个数相同//可以先任意遍历一条路径 比如走最右路径。查找black数量pNode cur = root;int blackCount = 0;while (cur){if (cur->_color == BLACK)++blackCount;cur = cur->_right;}int k = 0;return _isRBTree(root, k, blackCount);}bool _isRBTree(pNode root, int curBlackCount, int totalBlackCout)//curBlackCount:走到当前节点黑色个数{//每条路径上黑色个数相同//没有连续红色结点//一条路径走完if (root == nullptr){if (curBlackCount != totalBlackCout){cout << "每条路径-黑色结点个数不同" << endl;return false;}return true;}if (root->_color == BLACK)++curBlackCount;//没有红色连续pNode parent = root->_parent;if (parent->_color == RED && root->_color == RED){cout << "有连续的红色结点" << endl;return false;}return _isRBTree(root->_left, curBlackCount, totalBlackCout) && _isRBTree(root->_right, curBlackCount, totalBlackCout);}private:pNode _header;
};九、key,value 结构红黑树整体代码
#pragma once
#include<iostream>
using namespace std;//定义颜色
enum Color
{RED,BLACK,
};// 定义节点
template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 情况一 uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// 情况二if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}// 情况三else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){uncle->_col = parent->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{// g// p// cif (cur == parent->_left){RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}// g// p// celse{RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}}void RotateL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL)SubRL->_parent = parent;Node* ppNode = parent->_parent;SubR->_left = parent;parent->_parent = SubR;if (ppNode == nullptr){_root = SubR;SubR->_parent = nullptr;}else{if (parent == ppNode->_left){ppNode->_left = SubR;SubR->_parent = ppNode;}else{ppNode->_right = SubR;SubR->_parent = ppNode;}}}void RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR)SubLR->_parent = parent;Node* ppNode = parent->_parent;SubL->_right = parent;parent->_parent = SubL;if (ppNode == nullptr){_root = SubL;SubL->_parent = nullptr;}else{if (parent == ppNode->_left){ppNode->_left = SubL;}else{ppNode->_right = SubL;}SubL->_parent = ppNode;}}void InOrder(){_InOrder(_root);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}bool check(Node* root, int blackNum, int ref){if (root == nullptr){if (blackNum != ref){cout << "违反规则:本条路径的黑色节点的数量跟最左路径不相等" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则:出现连续红色节点" << endl;return false;}if (root->_col == BLACK)blackNum++;return check(root->_left, blackNum, ref)&& check(root->_right, blackNum, ref);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col != BLACK)return false;int ref = 0;// 统计黑节点的个数Node* left = _root;while (left){if (left->_col == BLACK)ref++;left = left->_left;}return check(_root, 0, ref);}
private:Node* _root = nullptr;
};
相关文章:

详解—[C++数据结构]—红黑树
目录 一、红黑树的概念 编辑二、红黑树的性质 三、红黑树节点的定义 四、红黑树结构 五、红黑树的插入操作 5.1. 按照二叉搜索的树规则插入新节点 5.2、检测新节点插入后,红黑树的性质是否造到破坏 情况一: cur为红,p为红,g为黑&…...

甘草书店记:6# 2023年10月31日 星期二 「梦想从来不是一夜之间实现的」
甘草书店 今天收到甘草书店第二版装修设计平面图,与理想空间越来越近。 于我而言,每一次世俗意义上所谓的成功都不如文艺作品中表现的那样让人欢腾雀跃。当你用尽120分努力,达到了冲刺满分的实力时,得个优秀的成绩也并不意外。 …...

基于Java SSM车辆租赁管理系统
现代生活方式下,人们经常需要租赁车辆,比如婚庆、自驾游等,车辆租赁公司应运而生,车辆租赁管理系统就是借助计算机对车辆租赁情况进行全面管理。系统的主要管理对象及操作有: 车辆信息:包括车辆类型、车辆名…...

侯捷C++八部曲(一,面向对象)
头文件和类的声明 inline inline修饰函数,是给编译器的一个建议,到底是否为inline由编译器来决定,inline修饰的函数在使用时是做简单的替换,这样就避免了一些函数栈空间的使用,从能提升效率。从另一种角度看ÿ…...

《数据库系统概论》学习笔记——王珊 萨师煊
第一章 绪论 一、数据库系统概述 1.数据库的4个基本概念 (1)数据 描述事物的符号记录称为数据 (2)数据库 存放数据的仓库 (3)数据库管理系统 主要功能: (1)数据定…...
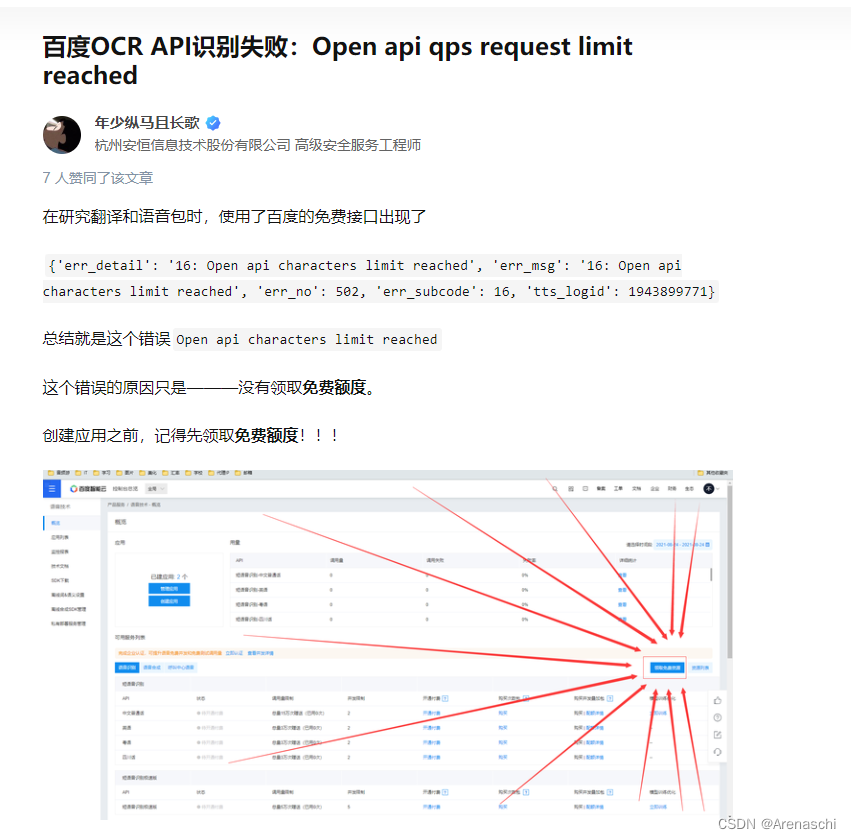
关于使用百度开发者平台处理语音朗读问题排查
错误信息:"convert_offline": false, "err_detail": "16: Open api characters limit reach 需要领取完 识别和合成都要有...

安全认证 | CISP和CISP-PTE的区别在哪里?
CISP和CISP-PTE的区别在哪里? 在国内安全信息认证体系中,虽然CISP认证与CISP-PTE认证都是中国信息安全测评中心负责颁发,均获得政府背景的认可,但二者还是有区别的。 今天就详细为大家介绍一下。 01 定义不同 ★ 注册信息安全专…...
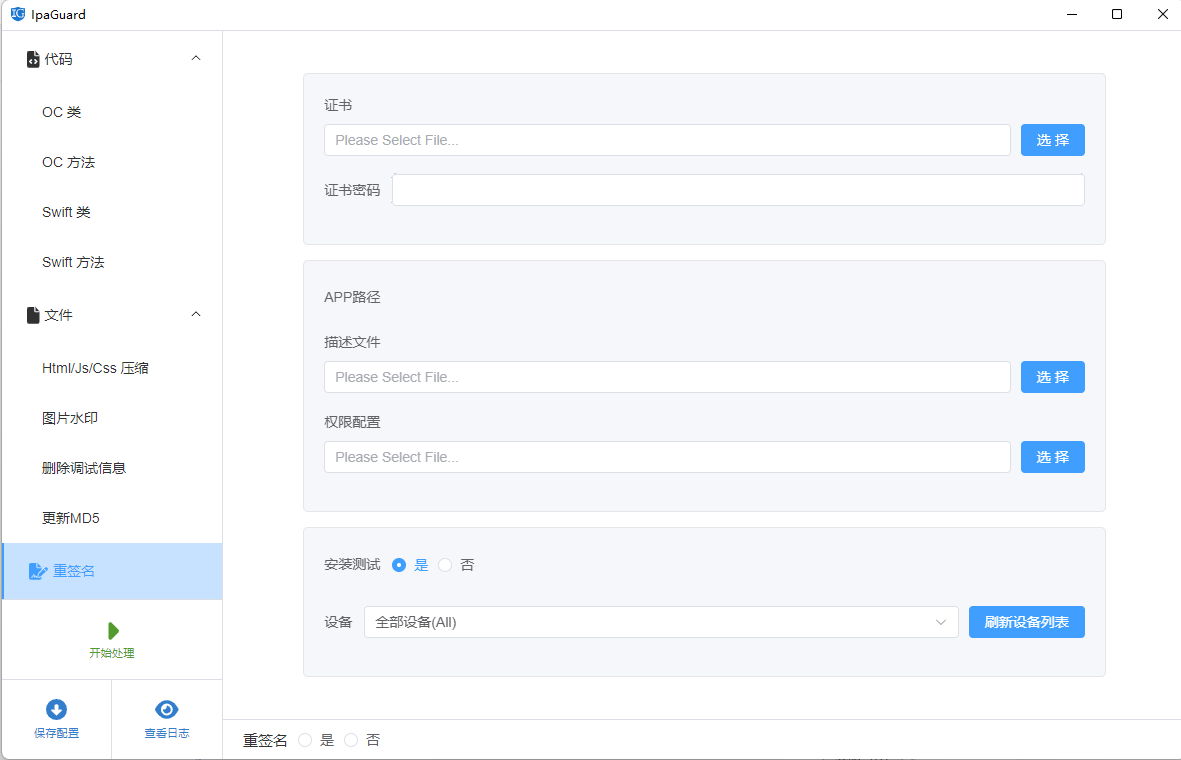
Unity3D 导出的apk进行混淆加固、保护与优化原理(防止反编译)
目录 前言: 准备资料: 正文: 1:打包一个带有签名的apk 2:对包进行反编译 3:使用ipaguard来对程序进行加固 前言: 对于辛辛苦苦完成的apk程序被人轻易的反编译了,那就得不偿…...

C语言扫雷小游戏
以下是一个简单的C语言扫雷小游戏的示例代码: #include <stdio.h>#include <stdlib.h>#include <time.h>#define BOARD_SIZE 10#define NUM_MINES 10int main() { int board[BOARD_SIZE][BOARD_SIZE]; int num_flags, num_clicks; int …...

用取样思想一探AIX上进程性能瓶颈
本篇文章也是我在解决客户问题时的一些思路,希望对读者有用。 本文与GDB也与DBX(AIX上的调试工具)无关,只是用到了前文《GDB技巧》中的思想:取样思想 客户问题: 原始问题是磁盘被占满了,通过…...
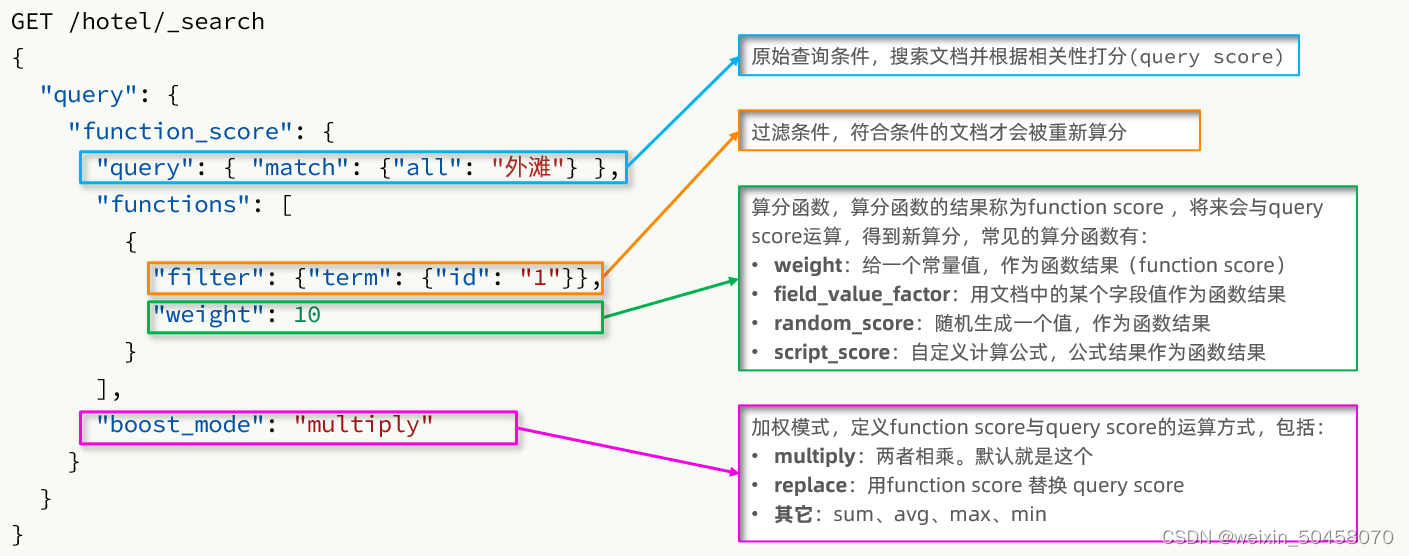
分布式搜索引擎elasticsearch(二)
1.DSL查询文档 elasticsearch的查询依然是基于JSON风格的DSL来实现的。 1.1.DSL查询分类 Elasticsearch提供了基于JSON的DSL(Domain Specific Language)来定义查询。常见的查询类型包括: 查询所有:查询出所有数据,一般测试用。例如:match_all 全文检索(full text)查…...

Tecplot绘制涡结构(Q准则)
文章目录 目的步骤1步骤2步骤3步骤4步骤5步骤6结果 目的 Tecplot绘制涡结构(Q准则判别)并用温度进行染色 Q准则计算公式 步骤1 步骤2 步骤3 步骤4 步骤5 步骤6 结果...
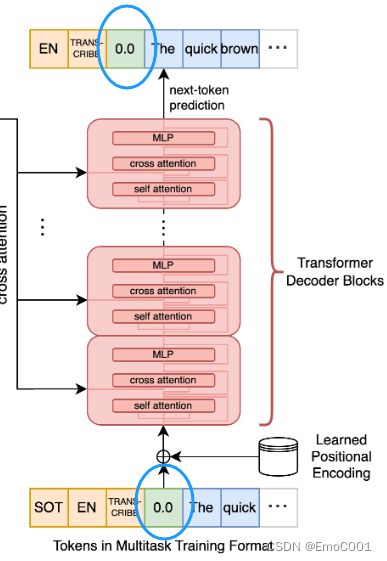
Whisper
文章目录 使后感Paper Review个人觉得有趣的Log Mel spectrogram & STFT Trainingcross-attention输入cross-attention输出positional encoding数据 Decoding为什么可以有时间戳的信息 Test code 使后感 因为运用里需要考虑到时效和准确性,类似于YOLOÿ…...

Android系统分析
Android工程师进阶第八课 AMS、WMS和PMS 一、Binder通信 【Android Framework系列】第2章 Binder机制大全_android binder-CSDN博客 Android Binder机制浅谈以及使用Binder进行跨进程通信的俩种方式(AIDL以及直接利用Binder的transact方法实现)_bind…...

五、关闭三台虚拟机的防火墙和Selinux
目录 1、关闭每台虚拟机的防火墙 2、关闭每台虚拟机的Selinux 2.1 什么是SELinux...

【从零开始学习Redis | 第六篇】爆改Setnx实现分布式锁
前言: 在Java后端业务中, 如果我们开启了均衡负载模式,也就是多台服务器处理前端的请求,就会产生一个问题:多台服务器就会有多个JVM,多个JVM就会导致服务器集群下的并发问题。我们在这里提出的解决思路是把…...

Kubernetes学习笔记-Part.05 基础环境准备
目录 Part.01 Kubernets与docker Part.02 Docker版本 Part.03 Kubernetes原理 Part.04 资源规划 Part.05 基础环境准备 Part.06 Docker安装 Part.07 Harbor搭建 Part.08 K8s环境安装 Part.09 K8s集群构建 Part.10 容器回退 第五章 基础环境准备 5.1.SSH免密登录 在master01、…...

语义分割 DeepLab V1网络学习笔记 (附代码)
论文地址:https://arxiv.org/abs/1412.7062 代码地址:GitHub - TheLegendAli/DeepLab-Context 1.是什么? DeepLab V1是一种基于VGG模型的语义分割模型,它使用了空洞卷积和全连接条件随机(CRF)来提高分割…...
java设计模式学习之【建造者模式】
文章目录 引言建造者模式简介定义与用途实现方式: 使用场景优势与劣势建造者模式在spring中的应用CD(光盘)的模拟示例UML 订单系统的模拟示例UML 代码地址 引言 建造者模式在创建复杂对象时展现出其强大的能力,特别是当这些对象需…...

Spring Boot中的RabbitMQ死信队列魔法:从异常到延迟,一网打尽【RabbitMQ实战 一】
Spring Boot中的RabbitMQ死信队列魔法:从异常到延迟,一网打尽 前言第一:基础整合实现第二:处理消息消费异常第三:实现延迟消息处理第四:优雅的消息重试机制第五:异步处理超时消息第六࿱…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
