多重背包问题 一句话说清楚“二进制拆分“
目录
区别:
一句话说清楚:
板子:
区别:
得先懂完全背包问题完全背包问题 非零基础-CSDN博客
都是让背包内价值最大。
完全背包问题每种物品可以取无数次。而多重背包问题每件取的次数有限。
都可以用的最挫的方法就是0~k件去遍历。
完全背包问题可以推出公式优化(或者说逻辑上可以直接一次从前往后遍历)
而多重背包问题不好推公式。本文讲的是二进制拆分方法来优化(完全背包问题也可以用这个,但是不是最优)
可以参考大佬文章学习 背包九讲——全篇详细理解与代码实现-CSDN博客
练习题: P1776 宝物筛选 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
一句话说清楚:
一句话说清这个二进制拆分:
int 整形知道吧?只需要32位就可以表示 -2147483647 - 1 ~ 2147483647
有点感觉吗?
再细说:1可以表示1 , 2可以表示2 , 1和2一起可以表示3 ,但我们只需要用到两个数,不需要遍历1到3
板子:
目的:把num拆成二进制 (最后一位(即剩余)未必是2的倍数)
第 i 件物品 ,本次装 k 件 ,j 是当前背包大小
W 是背包大小
m[ i ]是该物品的数目,w[ i ]是该物品的大小 , v[ i ]是该物品的价值
num是最大数目 : 看能装多少 W / w[i] ,再看有多少m[ i ] 。数目够,就尽可能装。数目w[i]不够,那就全装进去。
vector<ll>dp(MAX);for (int i = 1; i <= n; i++){int num = min(m[i], W / w[i]);for (int k = 1; num > 0; k<<=1){if (k > num)k = num;num -= k;for (int j = W; j >= 0; j--){if (j - w[i] * k >= 0)dp[j] = max(dp[j], dp[j - w[i] * k] + v[i] * k);}} }if可以自行优化掉
ε≡٩(๑>₃<)۶ 一心向学,加油!
相关文章:

多重背包问题 一句话说清楚“二进制拆分“
目录 区别: 一句话说清楚: 板子: 区别: 得先懂完全背包问题完全背包问题 非零基础-CSDN博客 都是让背包内价值最大。 完全背包问题每种物品可以取无数次。而多重背包问题每件取的次数有限。 都可以用的最挫的方法就是0~k件去…...

nodejs微信小程序+python+PHP本科生优秀作业交流网站的设计与实现-计算机毕业设计推荐
通过软件的需求分析已经获得了系统的基本功能需求,根据需求,将本科生优秀作业交流网站功能模块主要分为管理员模块。管理员添加系统首页、个人中心、用户管理、作业分类管理、作业分享管理、论坛交流、投诉举报、系统管理等操作。 随着信息化社会的形成…...

使用git出现的问题
保证 首先保证自己的git已经下载 其次保证自己的gitee账号已经安装并且已经生成ssh公钥 保证自己要push的代码在要上传的文件夹内并且配置文件等都在父文件夹(也就是文件没有套着文件) 问题 1 $ git push origin master gitgitee.com: Permission de…...
)
rk3568 适配PCIE(二)
rk3568 适配pcie3.0 PCIe(Peripheral Component Interconnect Express)是一种用于连接计算机主板和其他设备的高速串行总线接口。PCIe 2.0和PCIe 3.0是两个不同版本的PCIe规范,它们在以下几个方面有所不同: 带宽:PCIe 2.0的理论带宽为每条通道5 Gbps,而PCIe 3.0的理论带…...

Java基础 进制
在Java中,可以使用不同的进制表示整数常量和字面量。 十进制(Decimal):默认为十进制,不需要添加前缀。例如:int num 10;二进制(Binary):以0b或0B作为前缀表示二进制。例…...

springboot中@Builder注解的详细用法实例,跟数据库结合。
在Spring Boot中,Builder注解是Lombok库提供的一个注解,用于生成带有Builder模式支持的构造器方法。通过Builder注解,可以简化对象的创建过程,特别适用于需要设置多个属性的情况。 下面是一个使用Builder注解的示例: …...

WT2605C蓝牙音频语音芯片:具备大功率IO驱动能力,引领音频技术新纪元
在当今的电子科技时代,功率强大的IO驱动能力成为音频设备性能的重要指标。近日,一款名为WT2605C的蓝牙音频语音芯片,以其最高可直接驱动64mA的大功率IO驱动能力,引起业界的广泛关注。这款芯片的出现,无疑将为音频设备的…...

【Java 基础】20 多线程操作方法
文章目录 1.获取和设置线程的名字1)获取默认名字2)获取自定义的名字 2.判断线程是否启动3.线程的强制执行4.让线程睡一会儿5.中断线程6.守护线程7.线程的礼让 前一节我们介绍了线程的定义、创建方法、状态以及各状态间的转换。在状态转换处只是简单的说明…...

SpringBoot使用mybatis-plus分页查询无效解决方案
问题概述 SpringBoot中使用mybatis-plus实现分页查询时,提供一个page分页对象和一个QueryWrapper条件类对象,在使用Service.page(page,queryWrapper)方法进行分页查询时,发现并未查询到分页的结果,反而是查询到全部符合条件的结果…...
)
QT 中 线程池 (备查)
QRunnable类 API 1)在Qt中使用线程池需要先创建任务,添加到线程池中的每一个任务都需要是一个 QRunnable 类型,因此在程序中需要创建子类继承 QRunnable 这个类。 2)然后重写 run() 方法,在这个函数中编写要在线程池中…...

LeetCode刷题笔记第71题:简化路径
LeetCode刷题笔记第71题:简化路径 题目 给定一个路径,简化路径 要求: 1、以’/‘开头 2、两个目录之间只有一个’/’ 3、不能以’/‘结尾 4、路径中不能有’.‘和’…’ 想法 利用栈的数据存储方式的思想,将路径字符顺序入栈遇…...
JavaScript <md5加密的两种不同输出结果分析>--案例(二点一)
前言: 问题是这样的,在浏览器中看到这段代码 然后在控制台进行输出.得到: 紧接着,就在,js文件里面进行转译: 可是,得到的结果是: 这是问题!!! 正题: 为什么相同的js代码,在 .js 文件中的输出与 Chrome 控制台中的输出不一样? 环境差异:不同的JavaScript环境&…...
『亚马逊云科技产品测评』活动征文|基于亚马逊EC2云服务器配置Nginx静态网页
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 亚马逊EC2云服务器(Elastic Compute Cloud)是亚马…...
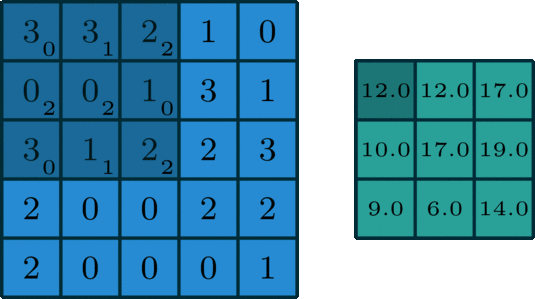
28、卷积 - 卷积的基础公式
本节推导一下卷积的基础公式,还是先上一张卷积运算的示意图图。 我们知道,一张图片有 3 个维度,分别是长、宽、通道。 这三个维度分别用 3 个字母代替,分别是 H(Height, 对应的是长这一维度), W(Width, 对应的是宽这一维度),C(Channel,对应的是通道这一维度)。 对于…...

Mac电脑vm虚拟机 VMware Fusion Pro中文 for mac
VMware Fusion Pro是一款功能强大的虚拟机软件,适用于需要在Mac电脑上运行其他操作系统的用户。它具有广泛的支持、快速稳定的特点以及多种高级功能,可以满足用户的各种需求和场景。 多操作系统支持:VMware Fusion Pro允许在Mac电脑上运行多…...

区块链技术的应用场景和优势
目录 一、引言 二、什么是区块链技术 三、区块链技术的应用场景 1.金融领域 (1)支付和清算:区块链可以为支付和金融结算提供更加快速、安全、便捷的方式。例如瑞士银行UBS和Deutsche Bank已经合作开发了基于区块链的支付和清算系统。 &a…...

java面试题-谈谈sql优化-mysql
远离八股文,面试大白话,通俗且易懂 看完后试着用自己的话复述出来。有问题请指出,有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来,大家一起解决。 这是面试总结出来的几点,每次问道都是这么回…...
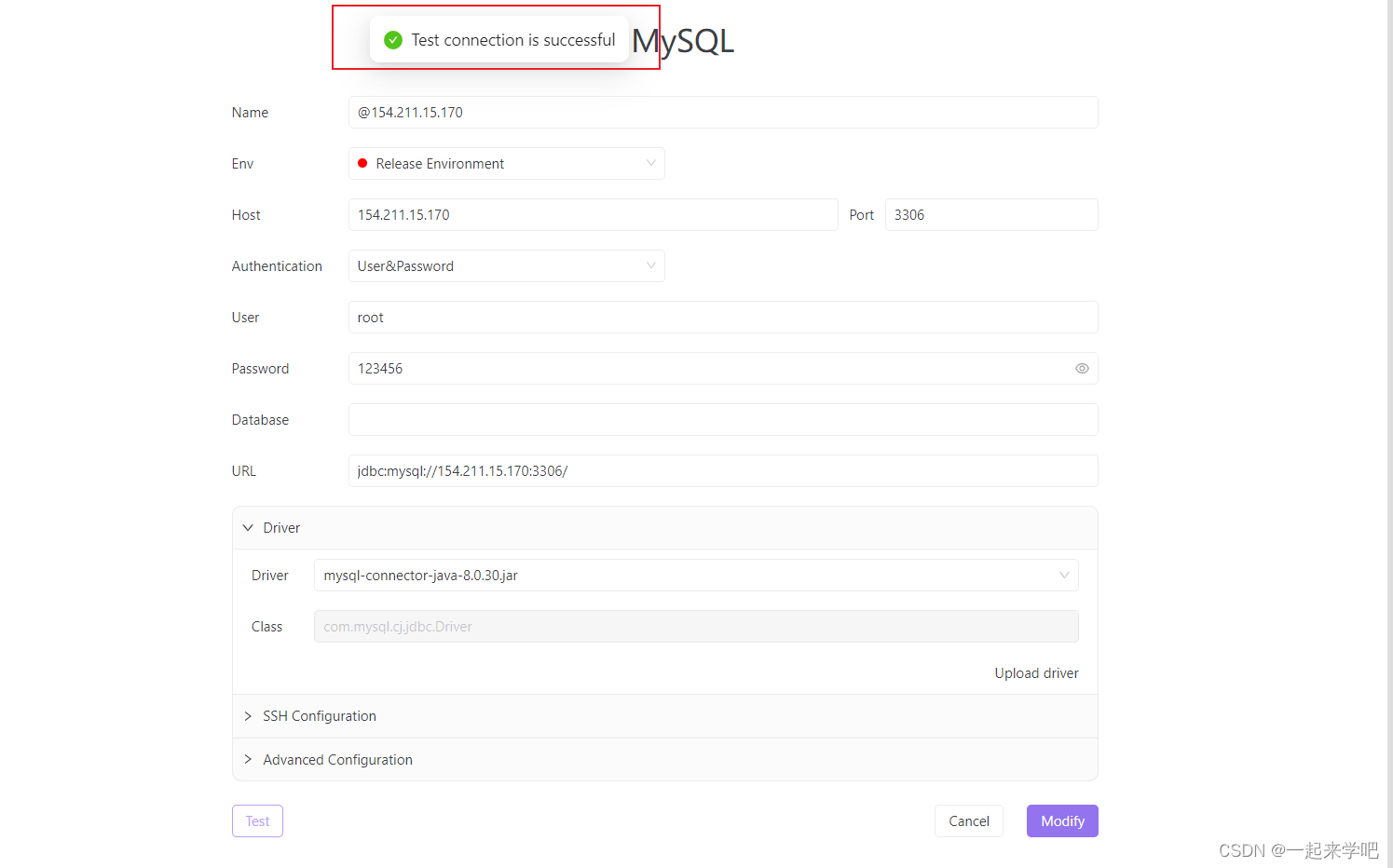
【Linux服务器Java环境搭建】07 在linux中安装MySql,以及对MySQL的配置与远程连接
【Linux服务器Java环境搭建】01购买云服务器以及在服务器中安装Linux系统 【Linux服务器Java环境搭建】02 通过xftp和xshell远程连接云服务器 【Linux服务器Java环境搭建】03 Git工具安装 【Linux服务器Java环境搭建】04 JDK安装(JAVA环境安装) 【Linux服…...
用 LangChain 搭建基于 Notion 文档的 RAG 应用
如何通过语言模型查询 Notion 文档?LangChain 和 Milvus 缺一不可。 在整个过程中,我们会将 LangChain 作为框架,Milvus 作为相似性搜索引擎,用二者搭建一个基本的检索增强生成(RAG)应用。在之前的文章中&a…...

QT中如何使用自定义控件
在 Qt 中,要使用自定义控件,需要遵循以下步骤: 创建自定义控件: 首先,需要创建一个自定义控件类,该类继承自 QWidget 或 QGraphicsItem 等基本控件类,并实现其相关函数和槽函数等。 在头文件中…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
