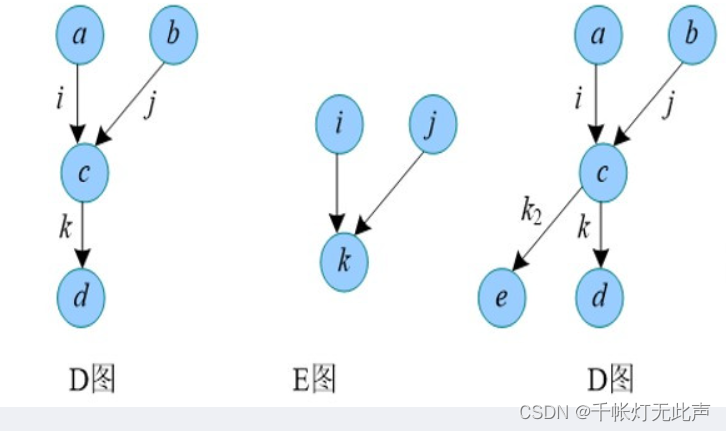
图的存储(邻接矩阵,边集数组,邻接表,链式前向星)
目录
🌼图的存储
(1)邻接矩阵
(2)边集数组
(3)邻接表
(4)链式前向星
😀刷题
🐍最大节点
🐍有向图 D 和 E
🐍奶牛排序
🌼图的存储
(1)邻接矩阵
adjacency matrix(邻接矩阵)
#define MaxVnum 100 // 节点数最大值
typedef char VexType; // 节点的数据类型, 根据需要定义
typedef int EdgeType; // 边上权值的数据类型; 不带权的图, 为0 / 1结构体
typedef struct {VexType Vex[MaxVnum]; // 节点类型 + 一维数组存储节点EdgeType Edge[MaxVnum][MaxVnum]; // 边上权值类型 + 邻接矩阵存储边int vexnum, edgenum; // 节点数, 边数
} AMGraph;算法
void CreateAMGraph(AMGraph &G) { // 引用传递, 直接修改对象本身// AMGraph 包含一维节点数组, 二维邻接矩阵数组, 节点数, 边数int i, j;VexType u, v; // 节点类型cin >> G.vexnum;cin >> G.edgenum;for (int i = 0; i < G.vexnum; i++) cin >> G.Vex[i]; // 输入节点for (int i = 0; i < G.vexnum; i++)for (int j = 0; j < G.vexnum; j++) G.Edge[i][j] = 0; // 初始化邻接矩阵所有值为 0while(G.edgenum--) {cin >> u >> v; // 'a' 'b' ...i = locatevex(G, u); // 查找节点 u 对应下标j = locatevex(G, v); // 查找节点 v 对应下标if(i != -1 && j != -1)G.Edge[i][j] = G.Edge[j][i] = 1; // 无向图两点连通}
}优点
(1)快速判断两点间,是否有边(Edge[i][j] == 1 有边)
(2)快速计算各节点的度
(无向图,邻接矩阵,第 i 行元素之和,就是节点 i 的 度)
(有向图,邻接矩阵,第 i 行的和为 出度,第 i 列的和为 入度)
缺点
(1)不利于增删节点(需要改变邻接矩阵大小,效率低)
(2)不利于访问邻接点
访问第 i 个点所有邻接点时,需要遍历第 i 行,时间复杂度 O(n)
访问所有点邻接点,时间复杂度 O(n^2)
(3)空间复杂度高,O(n^2)
初始可以这样定义👇(省去节点信息的查询步骤)
int M[m][n] = { {0,1,0,1}, {1,0,1,1}, {0,1,0,1}, {1,1,1,0} };直接定义一个邻接矩阵
(2)边集数组
数组存储每条边的起点和终点,以下是网的结构体定义(增加了一个权值域)
适用于 最小生成树 kruskal算法
struct Edge {int u;in v;int w;
} e[N*N];(3)邻接表
邻接表,包括节点和邻接点
节点
typedef struct VexNode { // 定义节点类型 VexType data; // VexType为节点信息的数据类型, 根据需要定义AdjNode *first; // 指向第1个邻接点
}VexNode;邻接点
typedef struct AdjNode { // 定义邻接点类型int v; // 下标vstruct AdjNode *next; // 指向下一个邻接点
}AdjNode;邻接表结构体
typedef struct {VexNode Vex[MaxVnum]; // 节点表int vexnum, edgenum; // 节点数, 边数
} ALGraph;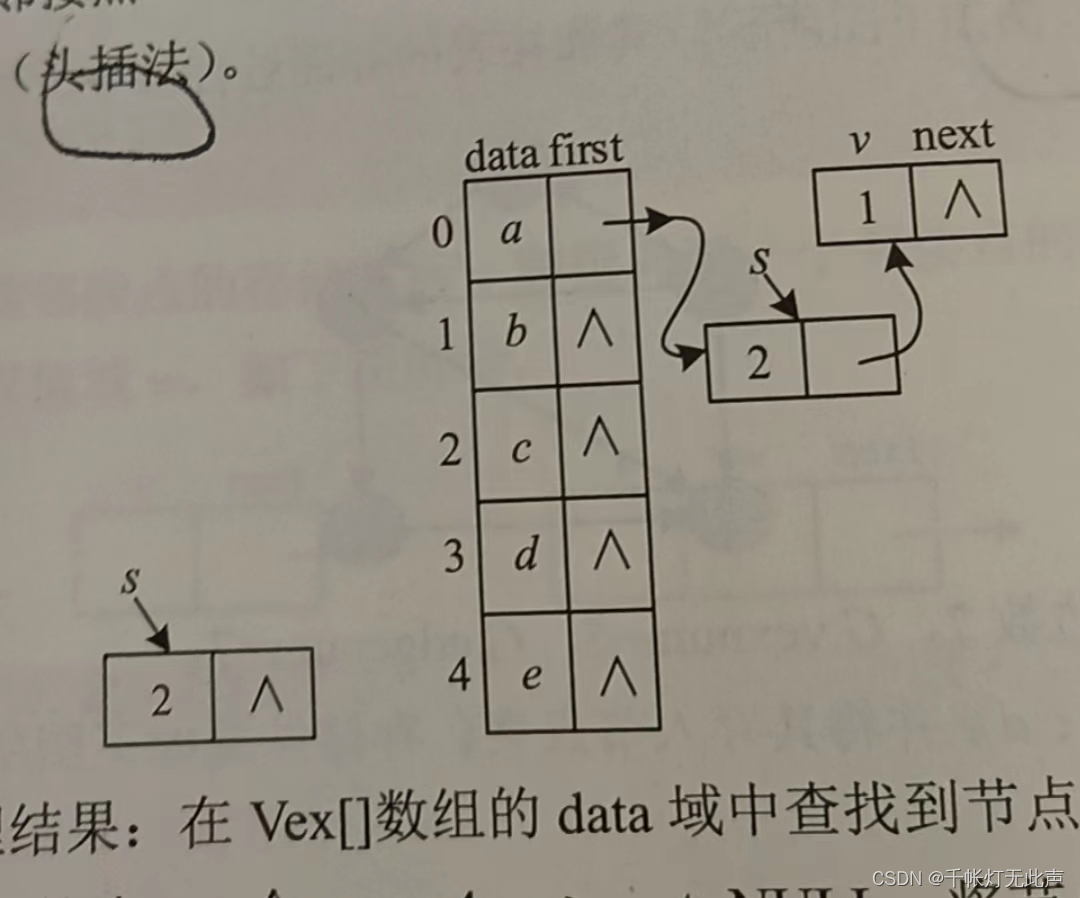
算法代码
void CreateALGraph(ALGraph &G) { // 创建有向图的邻接表VexType u, v; // 节点类型cout << "请输入节点数和边数:" << endl;cin >> G.vexnum >> G.edgenum;cout << "请输入节点信息:" << endl;for (int i = 0; i < G.vexnum; i++) // 节点数 vexnumcin >> G.Vex[i].data;for (int i = 0; i < G.vexnum; i++) G.Vex[i].first = NULL; // 下一个邻接点置空cout << "请依次输入每条边的两个节点 u, v" << endl;while (G.edgenum--) {cin >> u >> v;int i = locatevex(G, u); // 查找节点 u 的下标int j = locatevex(G, v); // 查找节点 v 的下标if (i != -1 && j != -1)insertedge(G, i, j); // 插入边// 无向图多插入 1 次}
}插入代码
void insertedge(ALGraph &G, int i, int j) // 头插法(插入一条边)
{AdjNode *s; // 新的邻接点s = new AdjNode; // 开辟内存// i 和 j相连, 所以是向 j 出边s->v = j; // 邻接点下标s->next = G.Vex[i].first; // 新的邻接点的下一个, 是原来节点 i 的下一个G.Vex[i].first = s; // 原来节点 i 的下一个, 变成邻接点
}邻接表优点
(1)便于增删节点
(2)便于访问所有邻接点( 时间复杂度O(n + e) )
(3)空间复杂度低( 节点表 n 个空间 ,无向图邻接点表 n + 2e 空间,有向图临界点表 n + e 空间,所以空间复杂度O(n + e) ),而邻接矩阵空间复杂度 O(n^2)
存储图,稀疏图 -> 邻接表,稠密图 -> 邻接矩阵
缺点
(1)不利于判断两节点是否有边(需要遍历该节点后,整条链表)
(2)不利于计算各节点的度
无向图为该节点后单链表节点数
有向图(邻接表)的出度为 单链表节点数,但不易求入度
有向图(逆邻接表)的入度为 单链表节点数,但不易求出度
总体上,邻接表,访问同一节点所有关联边时,仅需访问该点后单链表,这是一大优势
(4)链式前向星
链式前向星——最完美图解-腾讯云开发者社区-腾讯云 (tencent.com)
(👆算法训练营原文)
链式前向星--最通俗易懂的讲解-CSDN博客
链式前向星,即静态链表,边集数组 + 邻接表
可快速访问一个节点的所有邻接点
(1)边集数组:edge[i],第 i 条边
(2)头节点数组:head[k],存储以 顶点 k 为起点的第 1 条边的下标(edge[i] 中的 i,即第几条边)
结构体
struct node {int to, next, w;}edge[maxe]; // 边集数组, 对边数的设置要比 maxn*maxn大int head[maxn]; // 头节点数组next
与edge[cnt](第 cnt 条边)起点相同的上一条边的编号(之所以是上一条,不是下一条,因为邻接表采取头插法 -- 逆序)
添加边 u,v,w
void add(int u, int v, int w)
{// 第 cnt 条边edge[cnt].to = v; // 终点edge[cnt].w = w; // 权值edge[cnt].next = head[u]; // -1时没有上一条边head[u] = cnt++; // 先赋值, 后自增// 起点 u 为顶点的, 第一条边是 cnt, 然后 cnt++, 进入下一条边
}有向图:一次 add(u, v, w)
无向图:两次 add(u, v, w) 和 add(v, u, w)
访问一个节点 u 所有邻接点
当 edge[i].next != -1,说明还有邻接点
for (int i = head[u]; i != -1; i = edge[i].next)
{int v = edge[i].to; // 顶点 u 的邻接点int w = edge[i].w; // u-v 这条边的权值
}特点
(1)类似邻接表,头插法(倒序)进行链接 --> 边的输入顺序不同,创建的链式前向星也不同
(2)无向图的话,每输入一条边,需要添加 2 条边,又因为边从 0 开始,比如 edge[0]和edge[1],edge[2]和edge[3],4和5等等(即 0000和0001,0010和0011,0100和0101),此时,两条反向边,可以互相异或 1 得到另一条边,i 和 i^1
这个特性在网络流中较为常用(异或运算,不需要额外的存储 / 操作,节省空间和时间)
(3)整合了边集数组和邻接表,属于静态链表,不需要频繁创建节点
😀刷题
🐍最大节点
P3916 图的遍历 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路
本题,求,从节点 v 出发,能到达的最大节点 u
建立原图的反向图,即 add(u, v) 变成 add(v, u)
然后从节点 n 开始递归,一直到节点 1
对于当前最大节点 u,凡是能到达的节点 v,v能到达的最大节点就是 u
解释
结合图理解👇
节点 1 的第 1 条边是 edge[0],边的编号为 0,0号边即 节点1 到 节点2,距离(权值)为 5 的这条边,这条边的终点是 2(to),权值是 5(w),没有上一条边(next == -1)
if (ans[v]) return;两种可能的解释👆
(1)已经得到最远的点,避免后续多余的计算
(2)已经计算过的点,因为是反向的,此时再计算,可能会把无法到达的点算进去,导致结果错误
AC 代码
#include<iostream>
#include<cstdio> // scanf()
#include<cstring> // memset()
using namespace std;const int MAX = 100010;
int n, m, cnt = 0, head[MAX], ans[MAX];struct node
{int to, next;
}e[MAX];// 添加 u 到 v 的边
void add(int u, int v)
{e[cnt].to = v; // 终点e[cnt].next = head[u]; // 节点 u 的第一条边, 就是它的上一条边head[u] = cnt++; // 先赋值, 再自增
}// 递归遍历所有邻接边
// 注意是倒序反向遍历, 所以 u 是最远可到达的点
void dfs(int u, int v)
{if (ans[v]) return; // 已经得到最远点ans[v] = u; // 最远的点// 递归遍历所有邻接边for (int i = head[v]; i != -1; i = e[i].next) { // head[v] 节点 v 的第1条边int v1 = e[i].to; // 邻接点dfs(u, v1); // 最大节点 u 所能到达的点 v1}
}int main()
{scanf("%d%d", &n, &m);// 初始化 头节点 数组memset(head, -1, sizeof(head));// 添加反向边int u, v;while(m--) {scanf("%d%d", &u, &v);add(v, u);}// 倒序 dfs 递归for (int i = n; i >= 1; --i)dfs(i, i);// 输出for (int i = 1; i <= n; ++i)cout << ans[i] << " ";return 0;
}
🐍有向图 D 和 E
From D to E and Back - UVA 11175 - Virtual Judge (vjudge.net)
思路
把 D 的边缩成点,D 的边对应 E 的点
如果D存在边 i (u, v),j (v, w),那么 E 存在点 i, j,以及一条 i 到 j 的边
因为 D 和 E,都是有向图(关键)
所以, 若 D 中,边 i, j 有公共端点,那么 i 连接的边,j 一定也连接
换言之,E 中,点 i, j 有公共连接点 k,那么,此时如果 i 有邻接点 k2,j 必定也邻接 k2(因为 E 是有向图)
即,E中,点 i 和 点 k1 有边,点 j 和 k2 也有边,此时若点 i 和 k2 有边,j 必定也和 k2 有边
解释
第一个
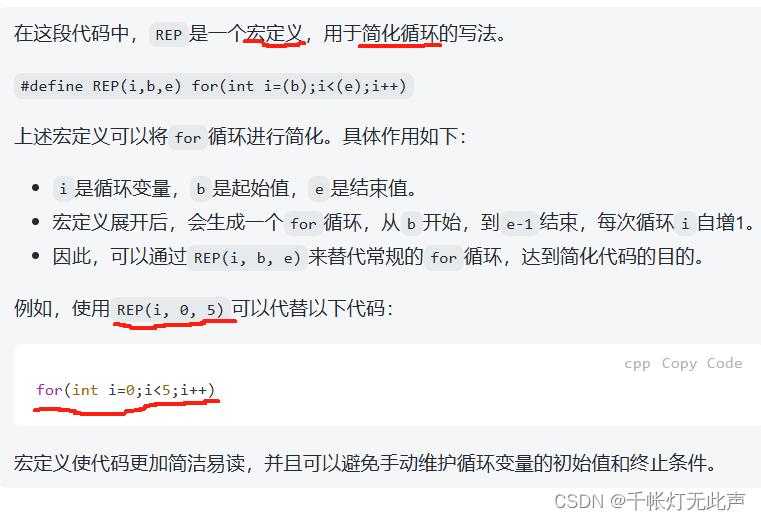
宏定义
第二个
REP(i,b,e)
REP后要紧跟着 (i,b,e),不要加个空格,否则报错:i was not defined in this scope
第三个
flag1, flag2 的声明,应该放在 i, j 两重循环内,而不是放在 check() 里
因为 return false,是针对相同的 i, j 去遍历每一个 k 的
第四个
每组测试,读入的是 m,边数
第五个
注意Yes,No之前有空格,直接复制题目会错
第六个
为什么用邻接矩阵存储呢,需要不断判断两个两个节点之间是否有边
AC 代码
远程 OJ 崩了,样例过了,就当过了吧
#include<bits/stdc++.h>
#define REP(i,b,e) for(int i=(b); i<(e); ++i)
using namespace std;const int N = 310;
int g[N][N], n, m; // g 邻接矩阵bool check()
{REP(i, 0, n) // 0~n-1REP(j, 0, n) { //0~n-1int flag1 = 0, flag2 = 0;REP(k, 0, n) { // 0~n-1if (g[i][k] && g[j][k]) flag1 = 1; // 共同邻接点if (g[i][k] ^ g[j][k]) flag2 = 1; // 一方有, 一方没有}if (flag1 && flag2) return false;}return true;
}int main()
{int T, cnt = 1;cin >> T;int x, y;while (T--) {memset(g, 0, sizeof(g)); // 初始化邻接矩阵cin >> n >> m;REP(i, 0, m) { // 读取 m 条边cin >> x >> y;g[x][y] = 1;}if (check())printf("Case #%d: Yes\n", cnt++);elseprintf("Case #%d: No\n", cnt++);}return 0;
}
🐍奶牛排序
Ranking the Cows - POJ 3275 - Virtual Judge (vjudge.net)
思路
样例
奶牛理解为有向图的节点,关系理解为边
对于 n 个节点的图,两两之间的关系有, 1 + ... + n-1 种,即 n(n-1) / 2
样例中 5 个节点,就有 10 种关系
然后根据给出的 5 条边,又能间接得到另外的 2 条边
所以10 - (5 + 3)= 3
还需要知道 3 种关系
位运算
那么,如何得到已知的关系是 7 种呢
每个节点用一个 bitset 表示👇目录中 2.4.7 bitset
STL入门 + 刷题(下)_千帐灯无此声的博客-CSDN博客
bitset<maxn>p[maxn]; // maxn表示位数, p[] 二进制数组初始化:p[i][i] = 1,表示自身可达(即自己和自己有关系)
输入
输入 2 1 (其他输入同理)
即 2 -> 1 的有向边,2 可达 1,那么 p[2][1] = 1,p[2] = 000110👇
右边第 0 位开始,第 2 位为 1,表示自身可达,第 1 位为 1,即节点 2 可达 节点 1
根据已知点找其他
if (p[i][k])p[i] |= p[k];// 等价于if (p[i][k])p[i] = p[i] | p[k];按位或:同时为 0 才为 0
可以间接找到每个点与其他点的关系👇
(比如节点 a 可达节点 b,b 可达 c,那么间接得到 a 也可达 c)
计算结果
两两间,总的关系数:n(n-1) / 2
用 ans 累计每个 bitset 数组 p[i] 中 1 的个数
由于 ans 中包括 n 种自己到自己的关系
所以已知关系为 ans - n
输出答案为 总数 - 已知数 =
n(n-1) / 2 - ans + n
解释
看懂代码后,有个疑问,如果最后还差 5 个关系,是否存在,只需要再调查 2 个关系,就能间接得到剩下 3 个关系的可能呢(可能是出题者结果导向,或者我的理解有偏差)
👆如果按这个意思,那么题目会复杂很多👆
坑
编号从 1 开始,所以如果你所有 for 循环都是 0 ~ n-1,就会 Wrong Answer
AC 代码
#include<iostream> // 编号 1 开始
#include<bitset>
using namespace std;const int N = 1010;
// N 表示长度为 N 的位集合
bitset<N> p[N]; // 数组 p 的每个元素都是 bitset<N> 类型, 即一个二进制数int main()
{int n, m, x, y, ans = 0;cin >> n >> m;// 初始化 bitset 数组for (int i = 1; i <= n; ++i)p[i][i] = 1; // 自己和自己有联系while (m--) {cin >> x >> y;p[x][y] = 1; // 节点 x 可达 y}// 间接求其他关系for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j) if (p[j][i])p[j] = p[j] | p[i];// 输出for (int i = 1; i <= n; ++i)ans += p[i].count(); // 统计每个 bitset 中 1 的个数cout << n*(n-1)/2 - ans + n << endl;return 0;
}除了常规意义的 邻接矩阵,边集数组,邻接表,链式前向星(存储图)外
我们还可以考虑 bitset,用二进制来存图
相关文章:

图的存储(邻接矩阵,边集数组,邻接表,链式前向星)
目录 🌼图的存储 (1)邻接矩阵 (2)边集数组 (3)邻接表 (4)链式前向星 😀刷题 🐍最大节点 🐍有向图 D 和 E 🐍奶牛…...
)
Linux 基础知识整理(二)
Linux系统目录结构 Linux采用的是树型结构。最上层是根目录,其他的所有目录都是从根目录出发而生成的。微软的DOS和windows也是采用树型结构,但是在DOS和 windows中这样的树型结构的根是磁盘分区的盘符,有几个分区就有几个树型结构ÿ…...

2024年值得关注的8个未来数据库
2024年值得关注的8个未来数据库 关系型数据库管理系统在数据库技术领域占据主导地位已经多年了。当SQL在1970年代首次出现时,关系型数据库管理系统的使用和受欢迎程度迅速提升。很快,MySQL成为了大多数公司和团队首选的数据库。 然而,2023年…...
C++新经典模板与泛型编程:将trait类模板用作模板参数
将trait类模板用作模板参数 template<typename T> struct SumFixedTraits;template<> struct SumFixedTraits<char> {using sumT int;static sumT initValue() {return 0;} };template<> struct SumFixedTraits<int> {using sumT __int64;sta…...

BUUCTF-[GYCTF2020]FlaskApp flask爆破pin
这道题不需要爆破也可以getshell ssti都给你了 {{((lipsum.__globals__.__builtins__[__import__](so[::-1])[popen]("\x63\x61\x74\x20\x2f\x74\x68\x69\x73\x5f\x69\x73\x5f\x74\x68\x65\x5f\x66\x6c\x61\x67\x2e\x74\x78\x74")).read())}} 但是学习记录一下pin…...

web前端实现LED功能、液晶显示时间、数字
MENU 效果演示html部分JavaScript部分css部分 效果演示 html部分 <div id"app"><!-- 页面 --><div class"time-box"><!-- 时 --><div class"house-box"><bit-component :num"houseTem"></bit…...

YOLOv8改进 | 2023 | DiverseBranchBlock多元分支模块(有效涨点)
一、本文介绍 本文带来的改进机制是YOLOv8模型与多元分支模块(Diverse Branch Block)的结合,Diverse Branch Block (DBB) 是一种用于增强卷积神经网络性能的结构重新参数化技术。这种技术的核心在于结合多样化的分支,这些分支具有…...
Spring Boot 3 整合 Spring Cache 与 Redis 缓存实战
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

kubeadm 安装k8s1.28.x 底层走containerd 容器
1. k8s1.28.x 的概述 1.1 k8s 1.28.x 更新 Kubernetes v1.28 是 2023 年的第二个大版本更新,包含了 46 项主要的更新。 而今年发布的第一个版本 v1.27 有近 60 项,所以可以看出来,在发布节奏调整后, 每个 Kubernetes 版本中都会包…...

“分割“安卓用户,对标iOS,鸿蒙崛起~
近期关于**“华为于明年推出不兼容安卓的鸿蒙版本”**的消息传出,引起了业界的热议关注。自从2019年8月,美国制裁下,华为不再能够获得谷歌安卓操作系统相关付费服务,如此情况下,华为“备胎”鸿蒙操作系统一夜转正。 华…...
【Vulnhub 靶场】【hacksudo: ProximaCentauri】【简单 - 中等】【20210608】
1、环境介绍 靶场介绍:https://www.vulnhub.com/entry/hacksudo-proximacentauri,709/ 靶场下载:https://download.vulnhub.com/hacksudo/hacksudo-ProximaCentauri.zip 靶场难度:简单 - 中等 发布日期:2021年06月08日 文件大小&…...

share pool的组成
share pool的组成 3块区域:free,library cache,row cache 通过查看v$librarycache视图,可以监控library cache的活动情况,进一步衡量share pool设置是否合理; 其中reloads列,表示对象被重新加载的次数,在一个设置合…...

应用案例 | 基于三维视觉的汽车零件自动化拧紧解决方案
Part.1 引言 随着人们生活水平的提高,汽车作为理想的代步工具,逐渐成为人们生活中不可或缺的一部分。汽车的广泛应用,大大增加了汽车制造业的负荷。因此,如何提高生产效率和汽车性能,成为汽车制造业的首要关注话题。…...

Redis server启动源码
入口main函数 src/redis.c文件main函数 int main(int argc, char **argv) {struct timeval tv;/* We need to initialize our libraries, and the server configuration. */// 初始化库 #ifdef INIT_SETPROCTITLE_REPLACEMENTspt_init(argc, argv); #endif//设置本地时间setl…...

C++基础 强制转换
目录 static_cast:static_cast(expression) const_cast dynamic_cast reinterpret_cast C 提供以下几类转换 static_cast:static_cast<type-id>(expression) tatic_cast 主要用于以下几种情况: 用于显式地将一个表达式转换为另一…...
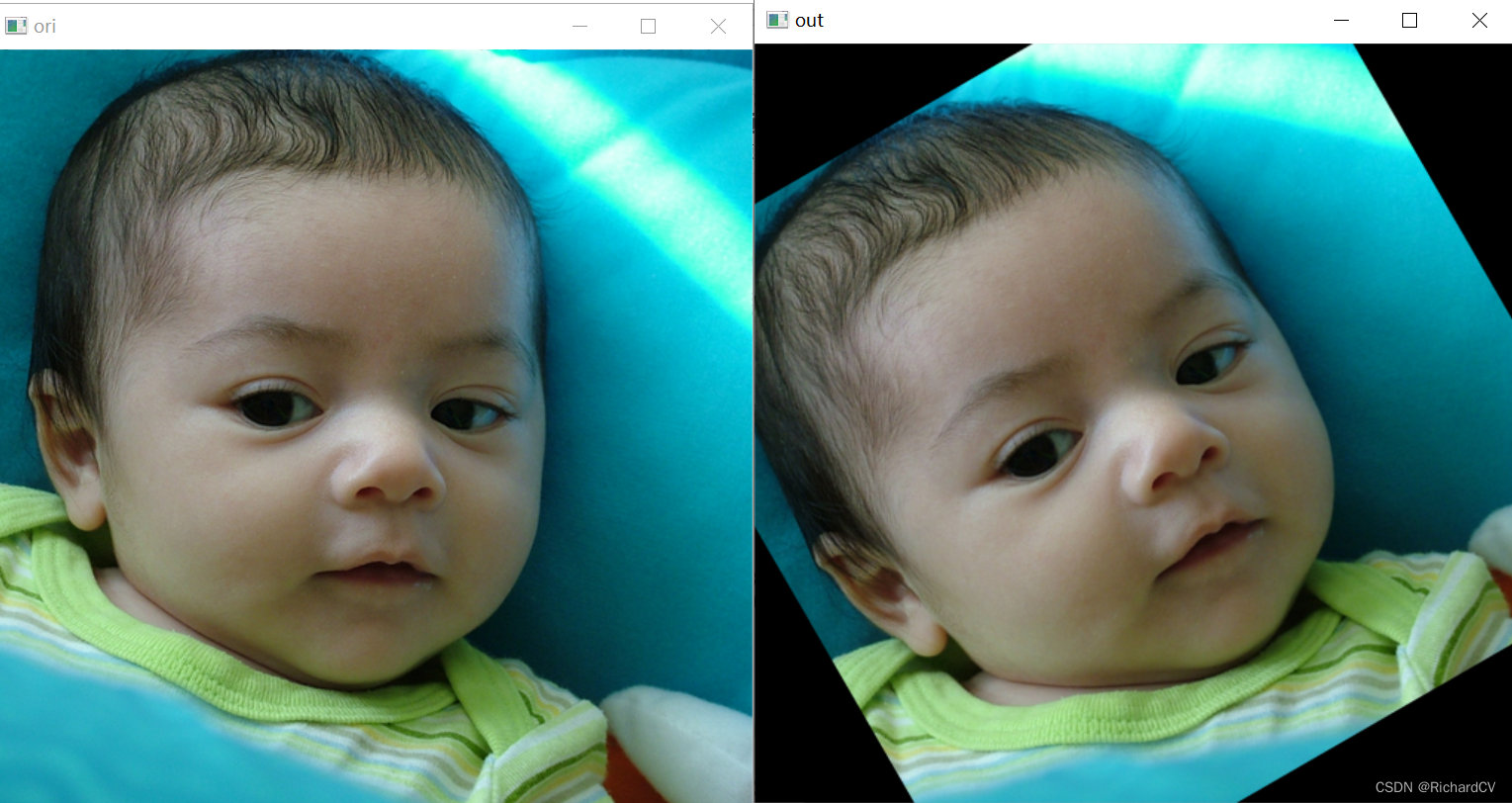
【python、opencv】opencv仿射变换原理及代码实现
opencv仿射变换原理 仿射变换是opencv的基本知识点,主要目的是将原始图片经过仿射变换矩阵,平移、缩放、旋转成目标图像。用数学公式表示就是坐标转换。 其中x,y是原始图像坐标,u,v是变换后的图像坐标。将公式转换为…...
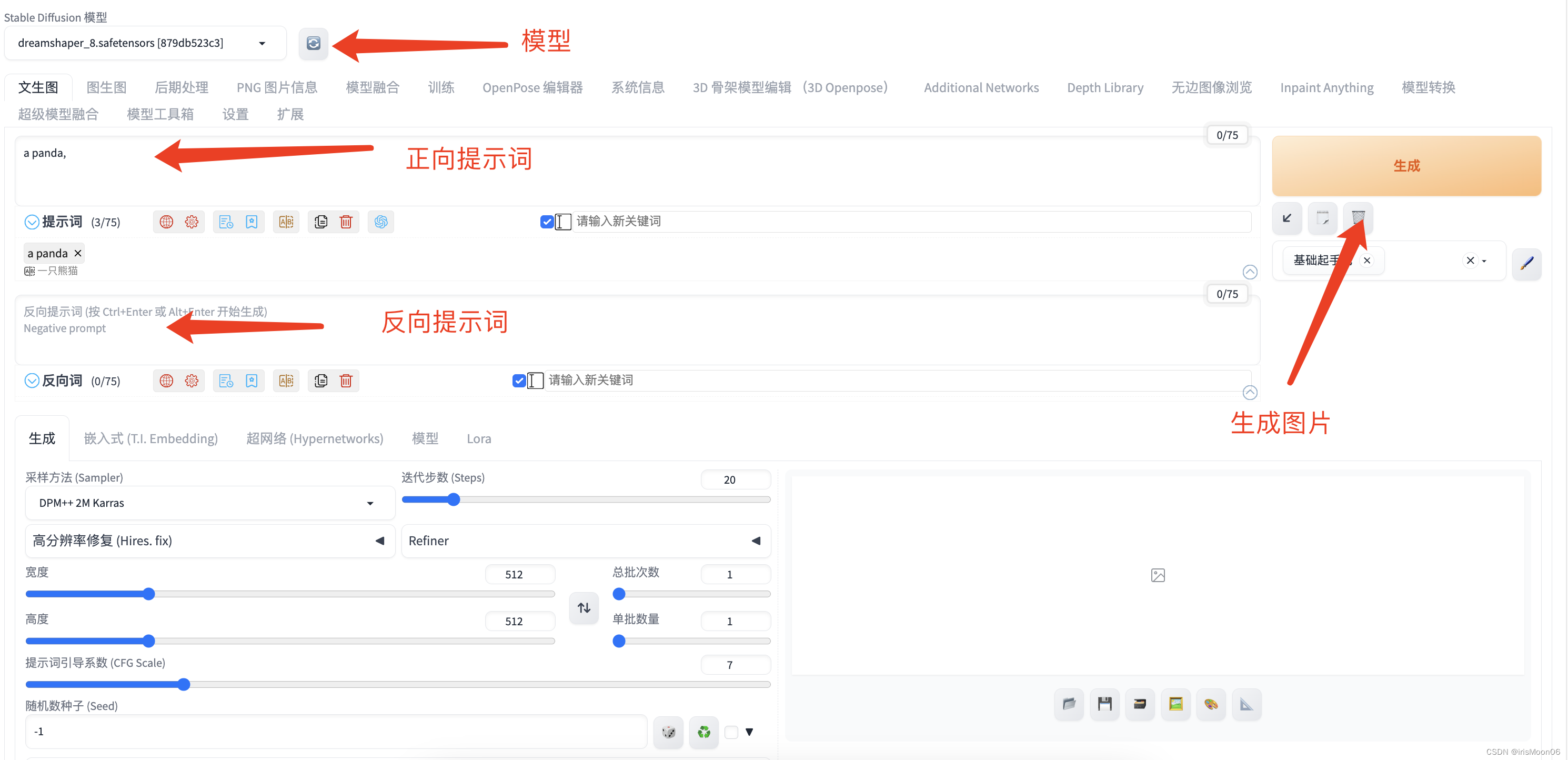
mac本地部署stable-diffusion
下载Homebrew /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)" ①输入“1”选择中科大版本,然后输入Y(YES),直接输入开机密码(不显示)然后回车确认,开始下载 ②…...
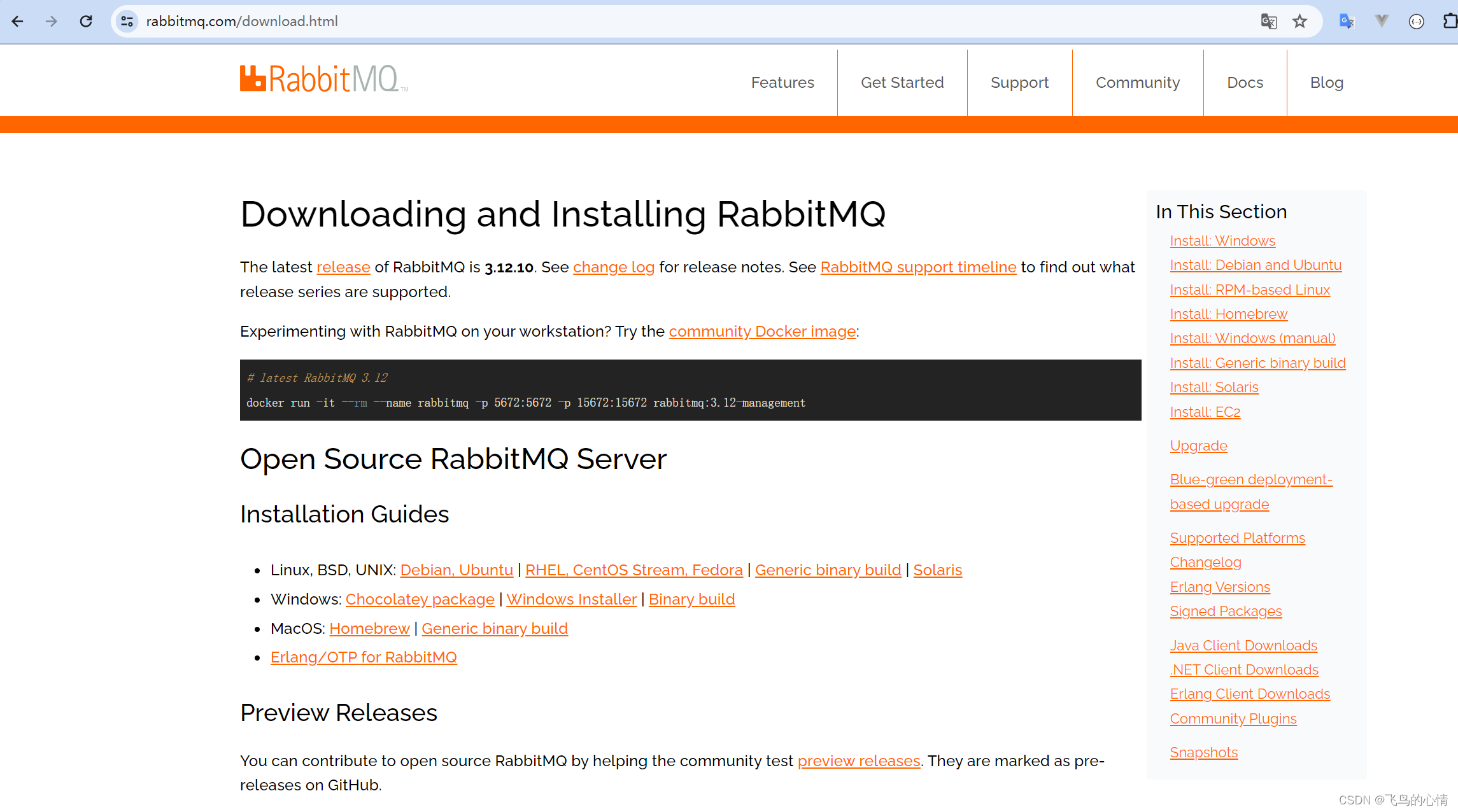
dockers安装rabbitmq
RabbitMQ: easy to use, flexible messaging and streaming — RabbitMQhttps://www.rabbitmq.com/ Downloading and Installing RabbitMQ — RabbitMQ docker run -it --rm --name rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq:3.12-management 之后参照:dock…...
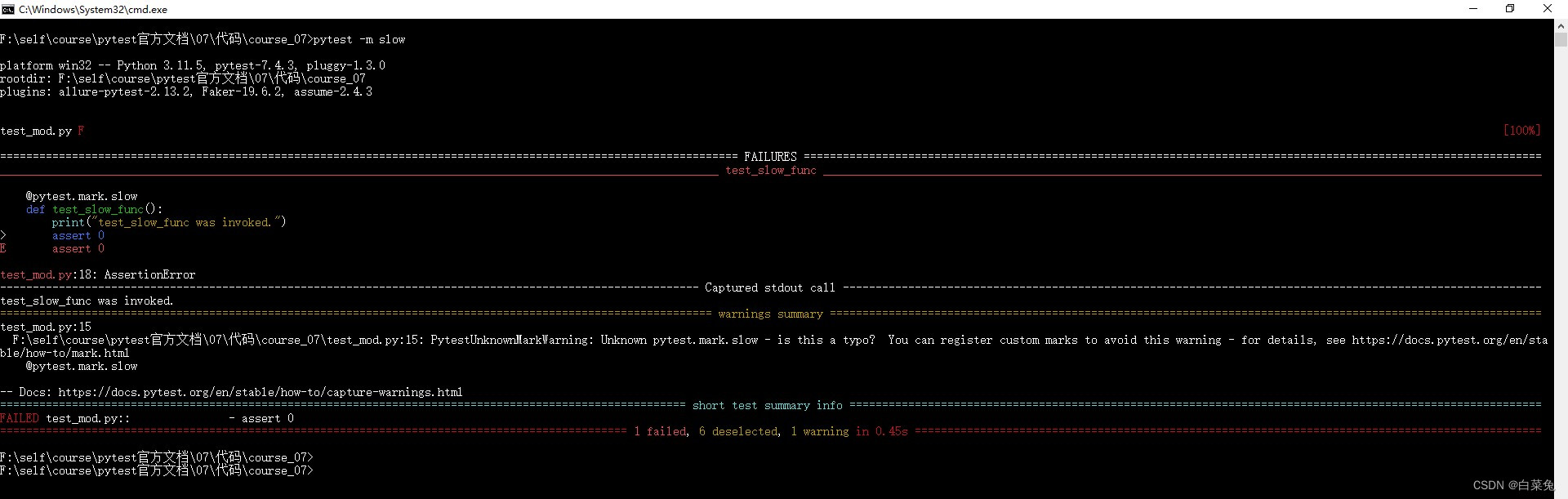
07、pytest指定要运行哪些用例
官方用例 # 目录结构 | |----test_mod.py | |----testing||----test_dir.py# content of test_mod.py import pytestdef func(x):return x 1def test_mod():print("test_mod function was invoked")assert func(3) 5def test_func():print("test_func was in…...

springboot集成cxf
<?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://ma…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...