【数据结构 — 排序 — 插入排序】
数据结构 — 排序 — 插入排序
- 一.排序
- 1.1.排序的概念及其运用
- 1.1.1排序的概念
- 1.1.2排序运用
- 1.1.3 常见的排序算法
- 二.插入排序
- 2.1.直接插入排序
- 2.1.1.算法讲解
- 2.1.2.代码实现
- 2.1.2.1.函数定义
- 2.1.2.2.算法接口实现
- 2.1.2.3.测试代码实现
- 2.1.2.4.测试展示
- 2.2.希尔排序
- 2.2.1.算法讲解
- 2.2.2.代码实现
- 2.2.2.1.函数定义
- 2.2.2.2.算法接口实现
- 2.2.2.3.测试代码实现
- 2.2.2.4.测试展示
一.排序
1.1.排序的概念及其运用
1.1.1排序的概念
排序: 所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.1.2排序运用


1.1.3 常见的排序算法

二.插入排序
2.1.直接插入排序
2.1.1.算法讲解
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
实际中我们玩扑克牌时,就用了插入排序的思想
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移

直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
2.1.2.代码实现
2.1.2.1.函数定义
Sort.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<time.h>//打印
void PrintArray(int* a, int n);
//插入排序
void InsertSort(int* a, int n);
2.1.2.2.算法接口实现
Sort.c
#include"Sort.h"//打印
void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}
//直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}
2.1.2.3.测试代码实现
test.c
#include"Sort.h"void TestInsertSort()
{int a[] = { 2,4,5,7,8,0,9,6,3,1 };printf("排序前:");PrintArray(a, sizeof(a) / sizeof(int));printf("\n");printf("直接插入排序:");InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestInsertSort();return 0;
}
2.1.2.4.测试展示

2.2.希尔排序
2.2.1.算法讲解
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。

希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定:
《数据结构(C语言版)》— 严蔚敏
《数据结构-用面相对象方法与C++描述》— 殷人昆
- 稳定性:不稳定
2.2.2.代码实现
2.2.2.1.函数定义
Sort.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<time.h>//打印
void PrintArray(int* a, int n);
//希尔排序
void ShellSort(int* a, int n);
2.2.2.2.算法接口实现
Sort.c
#include"Sort.h"//打印
void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}
//希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
2.2.2.3.测试代码实现
test.c
#include"Sort.h"void TestShellSort()
{int a[] = { 2,4,5,7,8,0,9,6,3,1 };printf("排序前:");PrintArray(a, sizeof(a) / sizeof(int));printf("\n");printf("希尔排序:");ShellSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestShellSort();return 0;
}
2.2.2.4.测试展示

相关文章:

【数据结构 — 排序 — 插入排序】
数据结构 — 排序 — 插入排序 一.排序1.1.排序的概念及其运用1.1.1排序的概念1.1.2排序运用1.1.3 常见的排序算法 二.插入排序2.1.直接插入排序2.1.1.算法讲解2.1.2.代码实现2.1.2.1.函数定义2.1.2.2.算法接口实现2.1.2.3.测试代码实现2.1.2.4.测试展示 2.2.希尔排序2.2.1.算法…...

物联网后端个人第十四周总结
物联网方面进度 1.登陆超时是因为后端运行的端口和前端监听的接口不一样,所以后端也没有报错,将二者修改一致即可 2.登录之后会进行平台的初始化,但是初始化的时候会卡住,此时只需要将路径的IP端口后边的内容去掉即可 3.阅读并完成了jetlinks…...

在uniapp中,可以使用那些预定义的样式类
u-flex:设置元素为弹性布局。u-flex-v:设置元素为纵向弹性布局。u-flex-h:设置元素为横向弹性布局。u-p-10:设置元素的上下左右边距为10rpx。u-p-t-10:设置元素的上边距为10rpx。u-p-b-10:设置元素的下边距…...

mybatis的数据库连接池
直接看原文 原文链接:【MyBatis】 连接池技术_mybatis自带连接池-CSDN博客 本文先不说springBoot整合mybatis后的 本文讲的是没有被springBoot整合前的mybatis自己的默认的连接池 --------------------------------------------------------------------------------------…...

Vue 的 el-select 下拉选项中,只有当文字超出时才显示提示框,未超出的则不显示
Vue 的 el-select 下拉选项中,只有当文字超出时才显示提示框,未超出的则不显示 <template><div><el-select v-model"selected" placeholder"请选择"><el-optionv-for"item in options":key"it…...

【Python】pptx文件转pdf
要将PPTX文件转换为PDF格式,你可以使用Python的python-pptx库来读取PPTX文件,然后使用comtypes库在Windows上或unoconv在Linux上来进行转换。但是,需要注意的是,comtypes依赖于Microsoft Office,而unoconv依赖于LibreO…...
response应用及重定向和request转发
请求和转发: response说明一、response文件下载二、response验证码实现1.前置知识:2.具体实现:3.知识总结 三、response重定向四、request转发五、重定向和转发的区别 response说明 response是指HttpServletResponse,该响应有很多的应用&…...
2)
CentOS常用基础命令大全(linux命令)2
CentOS常用基础命令大全(linux命令) 1.关机 (系统的关机、重启以及登出 ) 的命令 shutdown -h now 关闭系统(1) init 0 关闭系统(2) telinit 0 关闭系统(3) shutdown -h hours:minutes & 按预定时间关闭系统 shutdown -c 取消按预定时间关闭系统 sh…...

分析阿里巴巴的微服务依赖图和性能
论文对阿里巴巴集群中部署的大规模微服务进行了全面的研究。他们分析了 7 天内 20,000 多个微服务的行为,并根据收集的 100 亿条调用跟踪来分析它们的特征。该论文获得SOCC 2021最佳论文奖。 他们发现: 微服务图在运行时是动态的 大多数图形像树一样分…...
Linux——基本指令(一)
写在前面: 我们云服务器搭建的Linux系统,使用的镜像版本CentOS 7.6,使用的Xshell远程连接云服务器 前面我们使用超级管理员root账号登录,一般我们使用普通用户登录,那么如何创建新用户呢? 1.创建新用户 (…...
虚幻学习笔记10—C++函数与蓝图的通信
一、前言 除了上一章C变量与蓝图通信讲的变量能与蓝图通信外,还有函数和枚举也可以和蓝图通信。函数的关键字为”UFUNCTION“、枚举的关键字为”UENUM“。 二、实现 2.1、BlueprintCallable蓝图中调用 该函数时带执行的,带入如下。编译成功后在蓝图中输…...
)
无重复字符的最长子串(LeetCode 3)
文章目录 1.问题描述2.难度等级3.热门指数4.解题思路方法一:暴力法方法二:滑动窗口 参考文献 1.问题描述 给定一个字符串 s ,请你找出其中不含有重复字符的最长子串的长度。 s 由英文字母、数字、符号和空格组成。 示例 1: 输…...
交付《啤酒游戏经营决策沙盘》的项目
感谢首富客户连续两年的邀请,交付《啤酒游戏经营决策沙盘》的项目,下周一JSTO首席学习官Luna想让我分享下系统思考与投资理财,想到曾经看过的一本书《深度思维》,看到一些结构来预判未来。不仅仅可以应用在企业经营和组织发展上&a…...
油猴(Tampermonkey)浏览器插件简单自定义脚本开发
介绍 浏览器插件,包括油猴插件和其他插件,通过它们可以实现浏览器网页的定制化与功能增强。 其他插件一般只有某种具体的功能,且已经写死而不能更改,比如Adblock插件只用于去广告。 油猴插件是一款用于管理用户脚本的插件&…...

BGP综合
1、使用PreVal策略,确保R4通过R2到达192.168.10.0/24。 2、使用AS_Path策略,确保R4迪过R3到达192.168.11.0/24。 3、配置MED策略,确保R4通过R3到达192.168.12.0/24。 4、使用Local Preference策略,确保R1通过R2到达192.168.1.0…...

库函数qsort的使用及利用冒泡排序模拟实现qsort
文章目录 🚀前言🚀void*类型指针🚀库函数qsort的使用🚀利用冒泡排序实现库函数qsort() 🚀前言 今天阿辉将为大家介绍库函数qsort的使用,还包括利用冒泡排序模拟实现qsort以及void*类型的指针,关…...

mybatis和mybatisplus中对 同namespace 中id重复处理逻辑源码解析
一、背景 同事在同一个mapper.xml (namespace相同),复制了一个sql没有修改id,正常启动项目。但是我以前使用mybatis的时候如果在namespace相同情况下,id重复,项目会报错无法正常启动,后来看代码…...
linux下部署frp客户端服务端-内网穿透
简介 部署在公司内部局域网虚拟机上的服务需要在外网能够访问到,这不就是内网穿透的需求吗,之前通过路由器实现过,现在公司这块路由器不具备这个功能了,目前市面上一些主流的内网穿透工具有:Ngrok,Natapp&…...
Markdown to write
这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…...
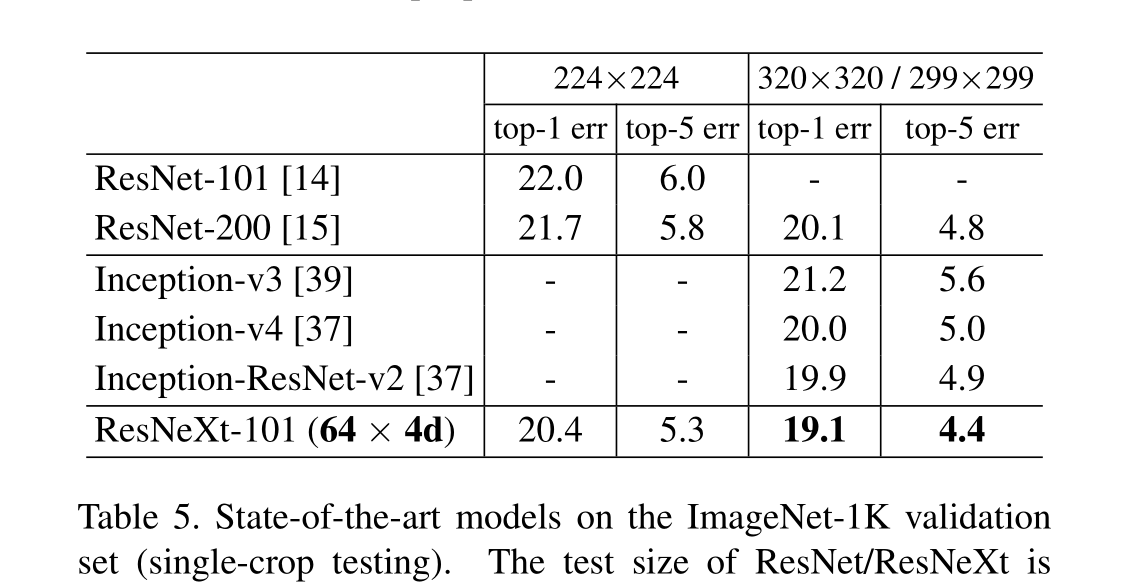
ResNeXt(2017)
文章目录 Abstract1. Introductionformer workour work 2. Related Work多分支卷积网络分组卷积压缩卷积网络Ensembling 3. Method3.1. Template3.2. Revisiting Simple Neurons3.3. Aggregated Transformations3.4. Model Capacity 4. Experiment 原文地址 源代码 Abstract 我…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...




