【数据结构】手撕排序

🔥博客主页: 小羊失眠啦.
🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》
❤️感谢大家点赞👍收藏⭐评论✍️

文章目录
- 一、排序的概念及其运用
- 1.1 排序的概念
- 1.2 常见的算法排序
- 二、 冒泡排序
- 三、直接插入排序
- 四、希尔排序
- 五、 选择排序
- 六、各大排序算法的复杂度和稳定性
一、排序的概念及其运用
1.1 排序的概念
排序:所谓排序就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的算法排序
排序算法分为比较类排序和非比较类排序,如下图所示:
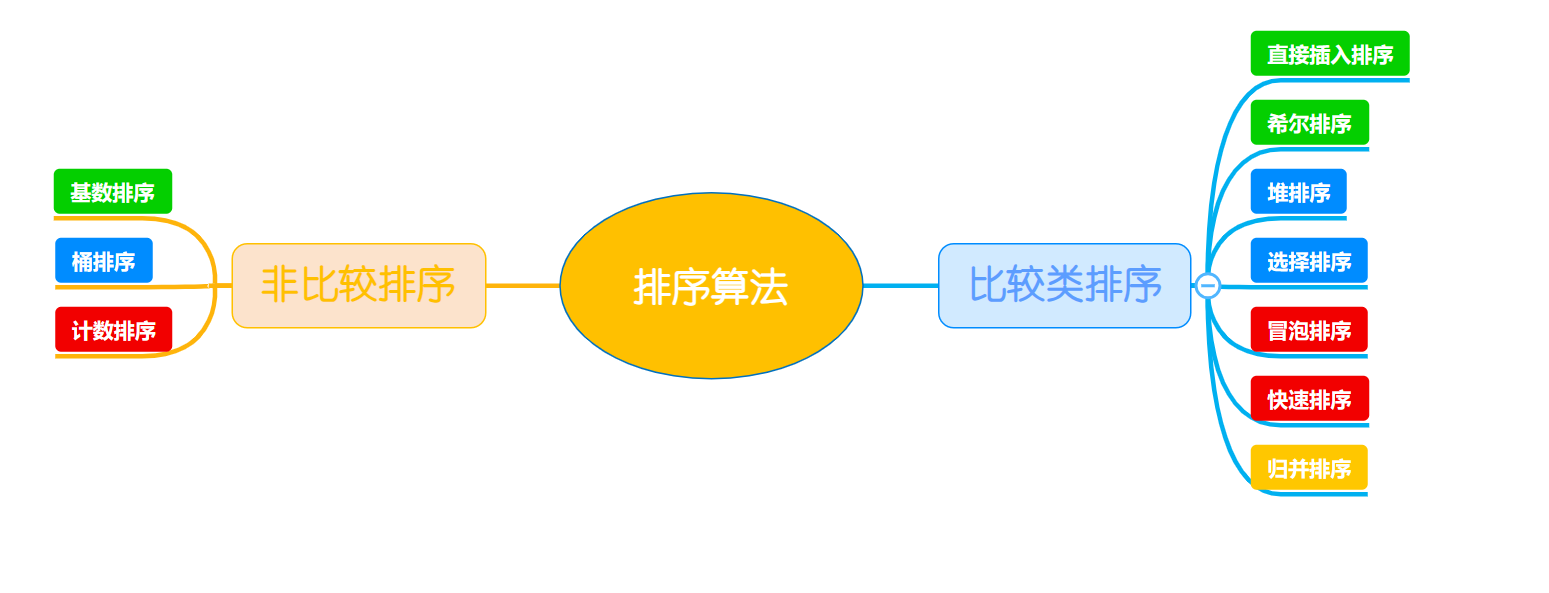
二、 冒泡排序
- 思想 : 在一个序列中,每次对序列中的相邻记录的键值大小进行比较,将
较大(升序)或较小(降序)的记录向后移动。如此循环,大/小的记录会慢慢“浮”到序列的后端,整个过程就像是冒泡一样,顾称之为冒泡排序。 - 冒泡过程:以下是对某个序列进行冒泡排序的过程
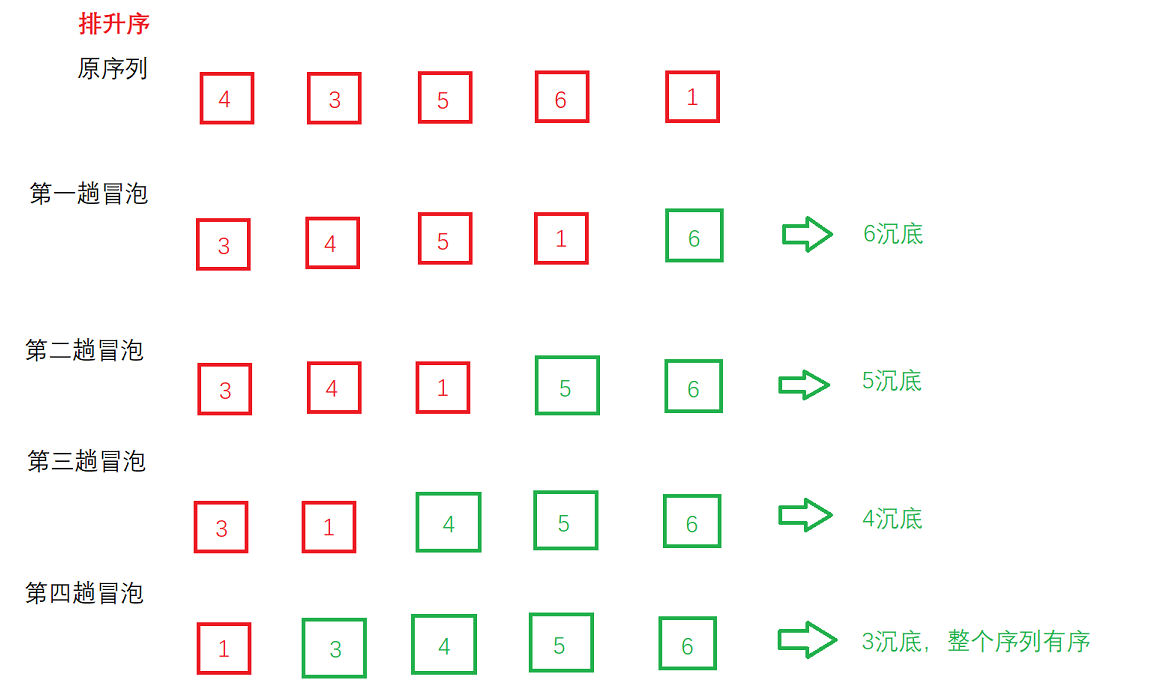
可以看出,对于上面具有5个元素的无序数组,我们通过4趟的冒泡后就将其变为有序数组,每一趟冒泡后都可以使最大的数沉底。
- 动图演示:我们可以通过一下动图感受一下冒泡两两比较的过程:
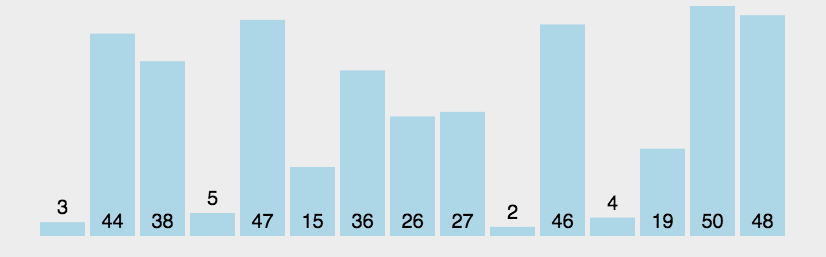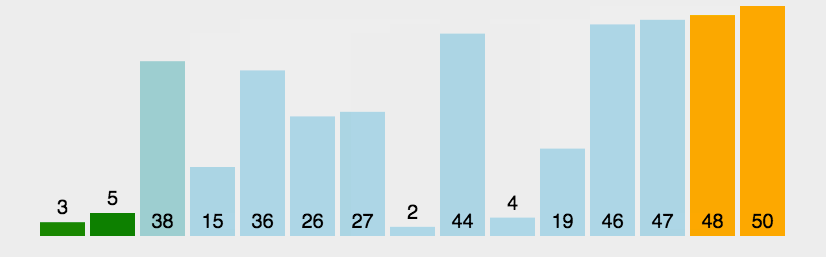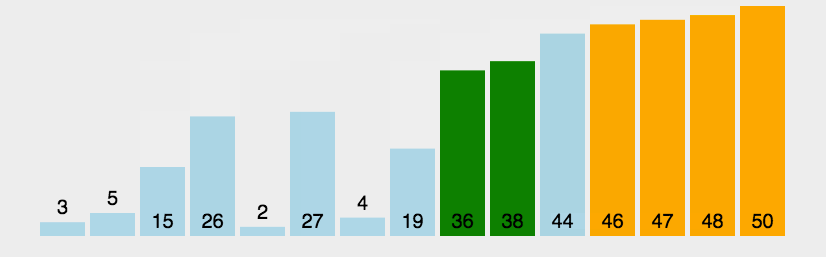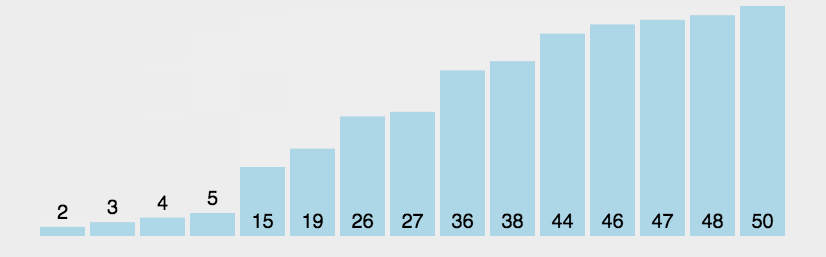
- 循环控制:很明显,我们需要两层循环来控制冒泡排序的过程。
内层循环控制当前趟的数据交换,外层循环控制冒泡排序的趟数。 - 外层循环结束条件:由于每一趟结束后都有一个数冒到序列后端,因此对于N个数的序列来说,一共需要N-1趟(只剩一个数不需要冒泡)。
for (int i = 0; i < n - 1; i++) //外层循环,N-1趟
{;
}
- 内层循环结束条件:内层循环用于数据的比较。已知N个数据共需比较N-1次,由于每一趟结束后就有数据到正确的位置,下一趟需要比较的数据个数就会少1,因此
每趟的比较次数随着趟数的增加呈递减趋势,初始为N-1次。
for (int i = 0; i < n - 1; i++) //外层循环,N-1趟
{for (int j = 0; j < n - 1 - i; j++) //内层循环,次数随趟数增加而递减,初始为N-1{;}
}
- 完整代码:
void swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void BubblingSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) //外层循环,N-1趟{for (int j = 0; j < n - 1 - i; j++) //内层循环,次数随趟数增加而递减,初始为N-1{if (a[j] > a[j + 1]) //升序排列,较大的往后移{swap(&a[j], &a[j + 1]); //交换}}}
}
- 改进优化:上面的代码还存在着改进空间,我们来看下面两个情景:
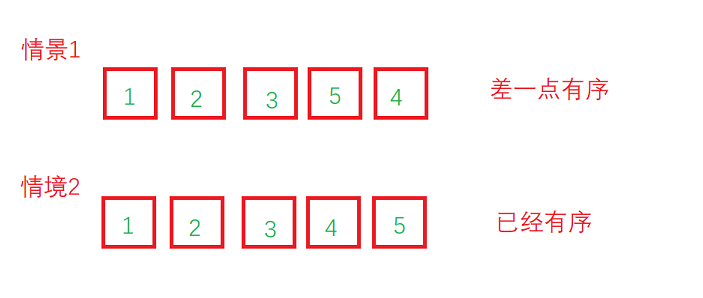
对于情境1,我们只需一趟冒泡即可让数组有序,而如果按照上面的代码,我们依旧要进行4趟的冒泡,即有三趟是无效的。
而情境2就更夸张了,数组已经有序,我们却傻乎乎的做了4趟无效冒泡。无疑是非常浪费时间的。
考虑到这些情况,我们提出了优化方案:
在每趟结束后判断一下当前趟是否发生了元素交换,如果没有,则说明序列已经有序了,及时止损,反之继续。优化后的代码如下:void swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp; }void BubblingSort(int* a, int n) {for (int i = 0; i < n - 1; i++) //外层循环,N-1趟{int flag = 0;for (int j = 0; j < n - 1 - i; j++) //内层循环,次数随趟数增加而递减,初始为N-1{if (a[j] > a[j + 1]) //升序排列,较大的往后移{swap(&a[j], &a[j + 1]); //交换flag = 1;}}if (flag == 0)break;} }
- 时间/空间复杂度:结合上面的图片和代码我们可以看出,总共N-1趟,每趟N-1,N-2…次比较,共比较 (N-1) + (N-2) + (N-3) + (N-4) + (N-5) + … + 1次,时间复杂度为O(N^2);而由于没有额外的辅助空间,空间复杂度为O(1)。
- 稳定性分析:由于我们是将较大的或较小的进行交换,当两个数相等时并不会进行交换,因而不会改变相同元素的先后次序,所以冒泡排序是稳定的排序。
三、直接插入排序
- 基本思想
插入排序的基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
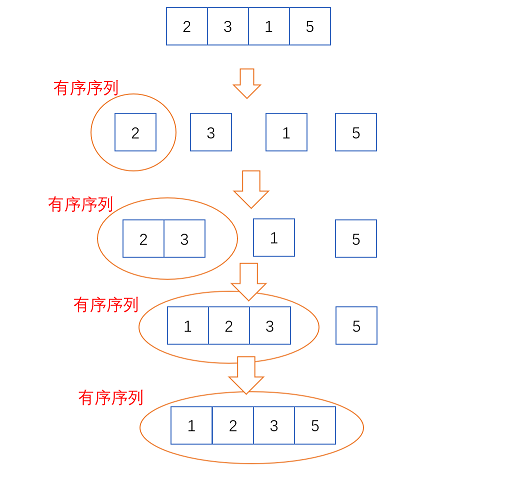
- 过程分析
我们可以将第一个元素作为一个有序序列,从第二个元素开始插入到这个有序序列中,过程如下:
以升序为例:
当插入第i个元素时(i>=1),说明前面的array[0],array[1],…,array[i-1]已经排好序,我们将array[i]位置的值从后往前与array[i-1],array[i-2],…依次进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。
为什么不从前往后开始进行比较?
如果我们从前往后进行比较,当找到插入位置时,根据顺序表的插入我们知道:必须先将后面的元素全部后移,而后移又不能从前往后移,否则会造成元素覆盖,我们必须从后往前移动。折腾了半天又要
从后往前遍历,那为什么不一开始就从后往前比较,在比较的同时一并挪动元素,何乐而不为呢?
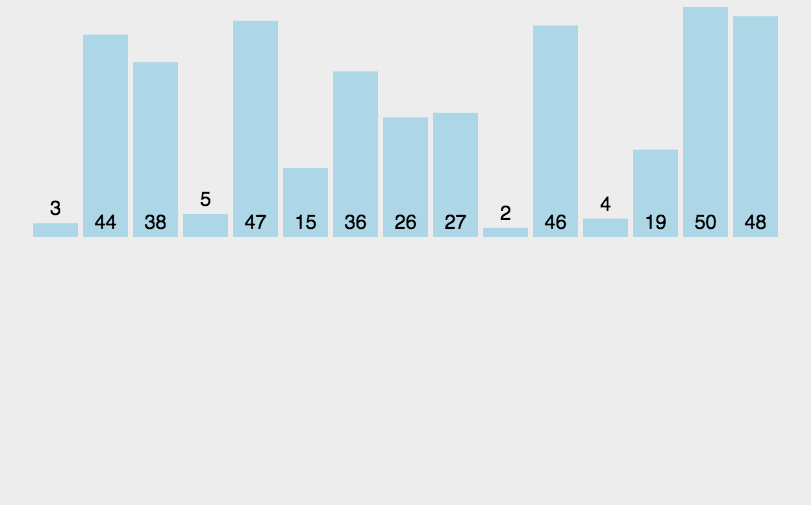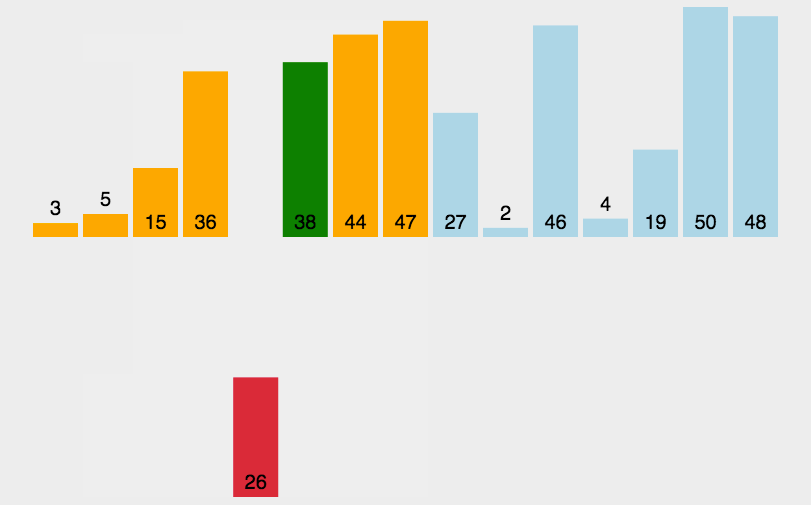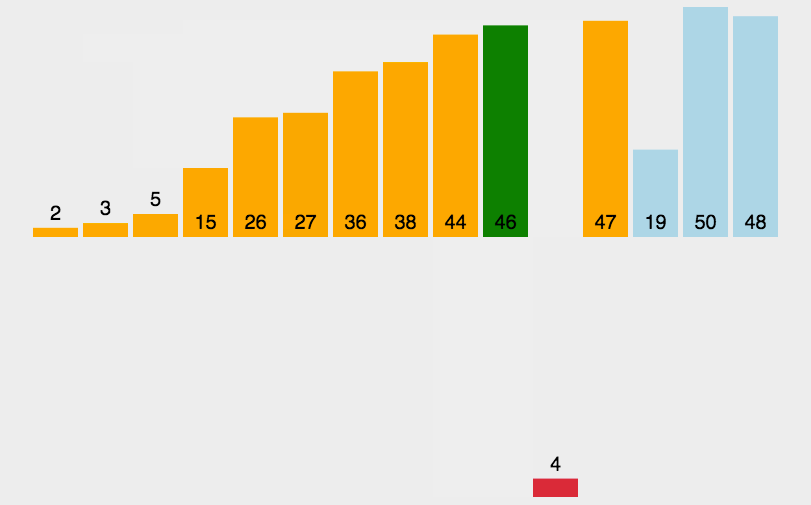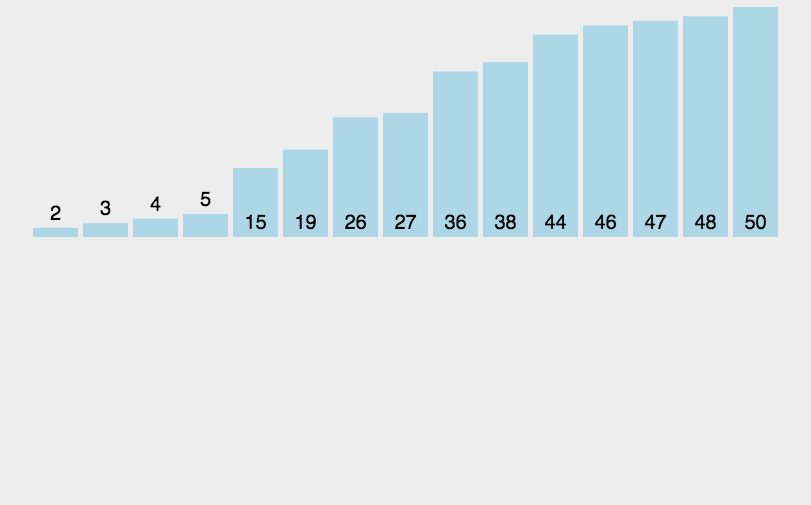
单趟插入动图:
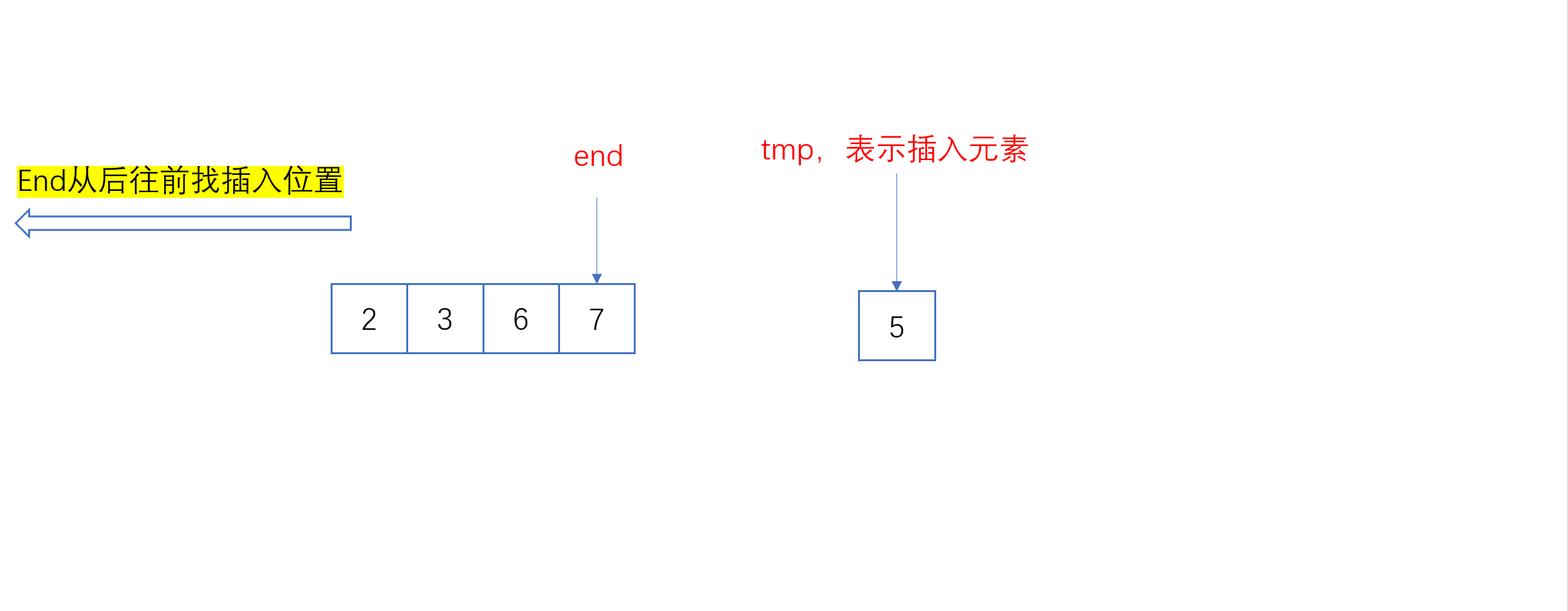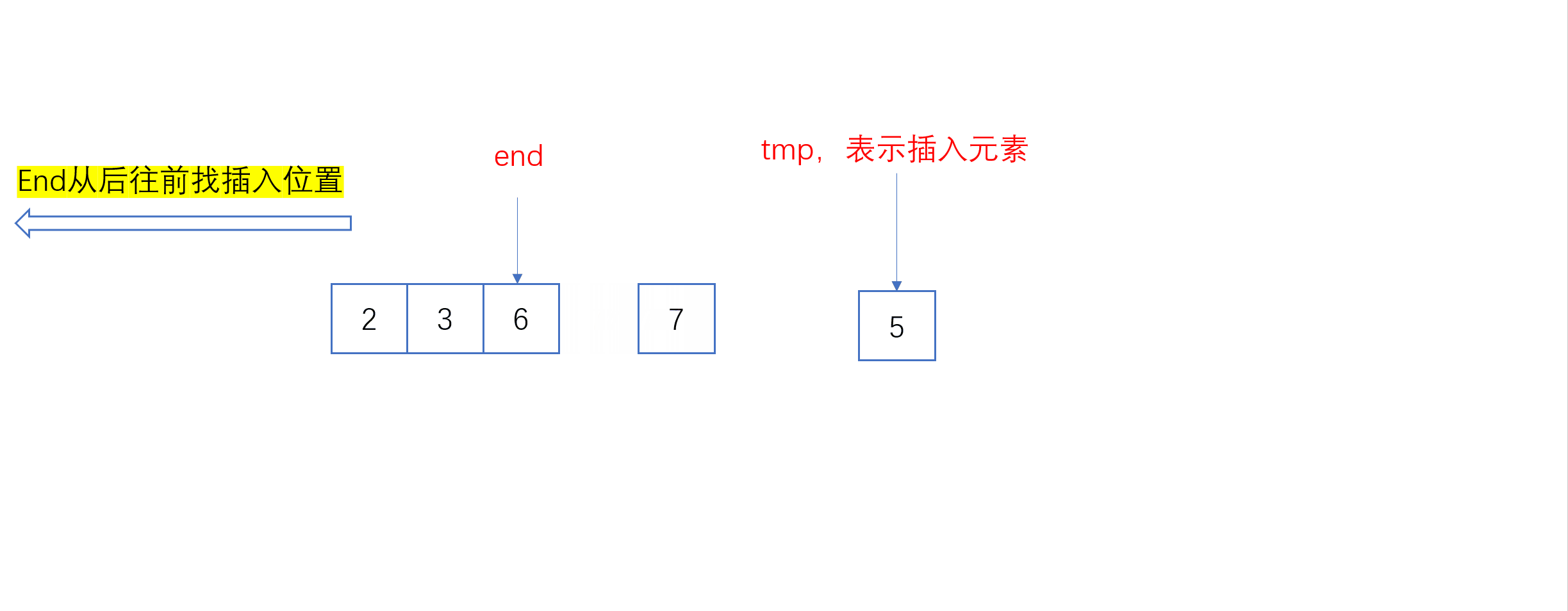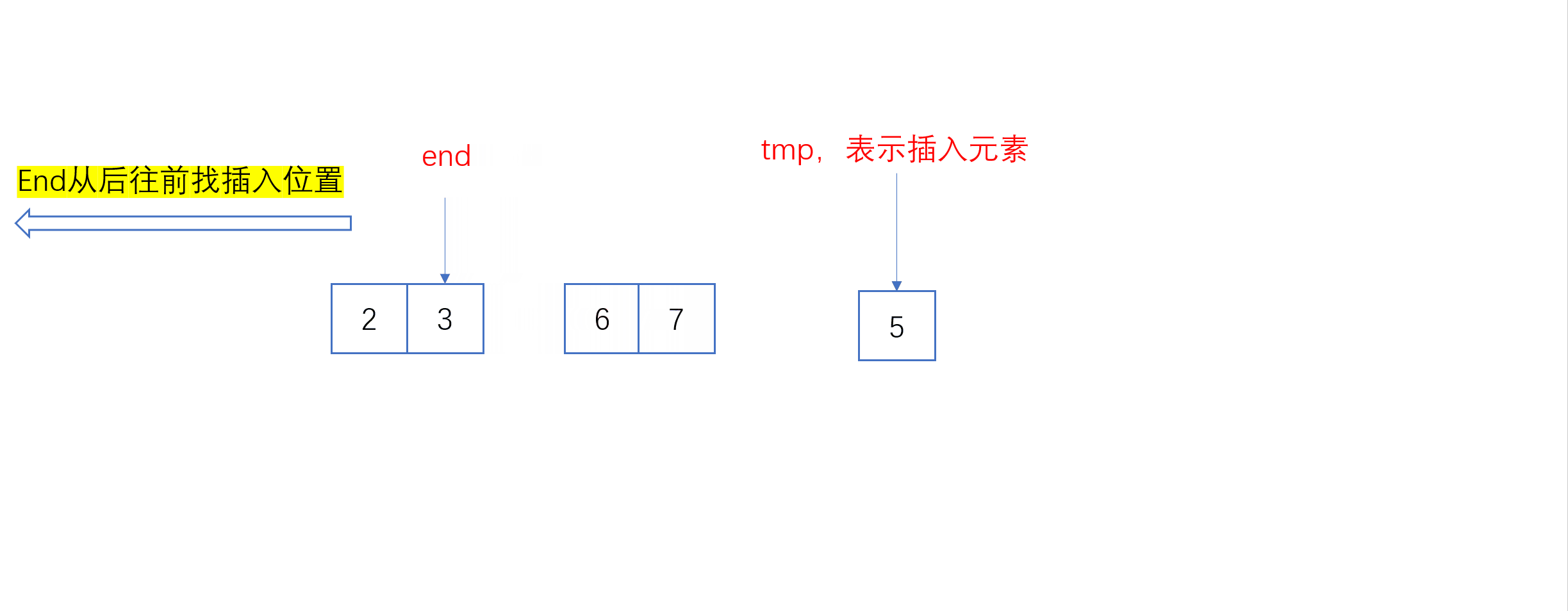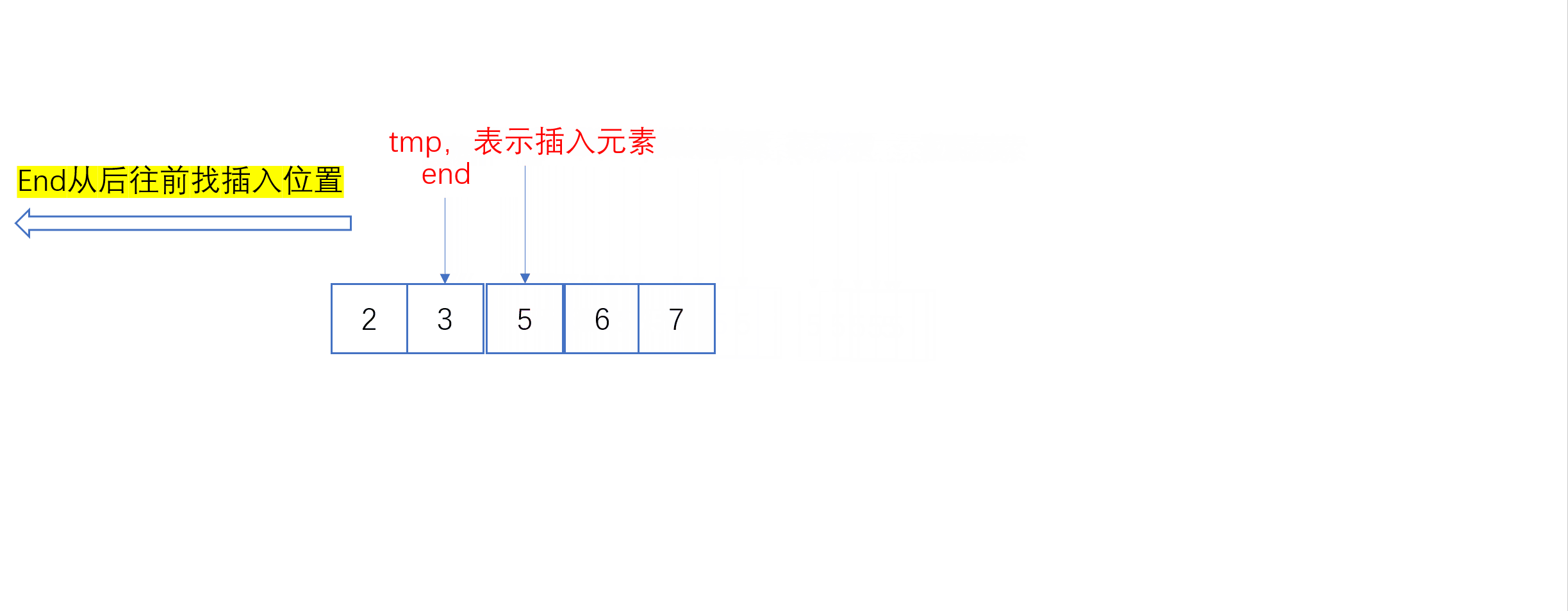
全过程动图:
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp)a[end + 1] = a[end];elsebreak;end--;}a[end + 1] = tmp;}
}
复杂度/稳定性分析
复杂度:
根据上面的动图我们可以发现,当元素集合越接近有序,直接插入的时间效率越高,当元素集合已经有序时,时间复杂度便是O(N),即遍历一遍数组(最优情况)。
而时间复杂度我们看的是最坏情况,即数组元素逆序的情况。此时每次插入相当于头插,而头插的时间复杂度为O(N),因此总时间复杂度为O( 插入次数 * 单次插入时间复杂度 ) = O(N^2)。
而除了待排序数组之外只有常数级的辅助空间,空间复杂度为O(1)。
稳定性:
由于我们是大于tmp才进行元素挪动,当等于tmp时直接将tmp放到后方,不会对相同元素的顺序进行改变,因此直接插入排序是稳定的排序
四、希尔排序
- 基本思想
希尔排序又称缩小增量法,其基本思想是:选出一个整数gap表示增量,根据gap将待排序的记录分为gap组,所有距离为gap的记录分在同一组,然后对每一组进行直接插入排序。随着排序次数的增多,增量gap逐渐减少,当gap=1时,即所有记录分在同一组进行直接插入排序,排序完成后序列便有序了,算法结束。分组方法如下:
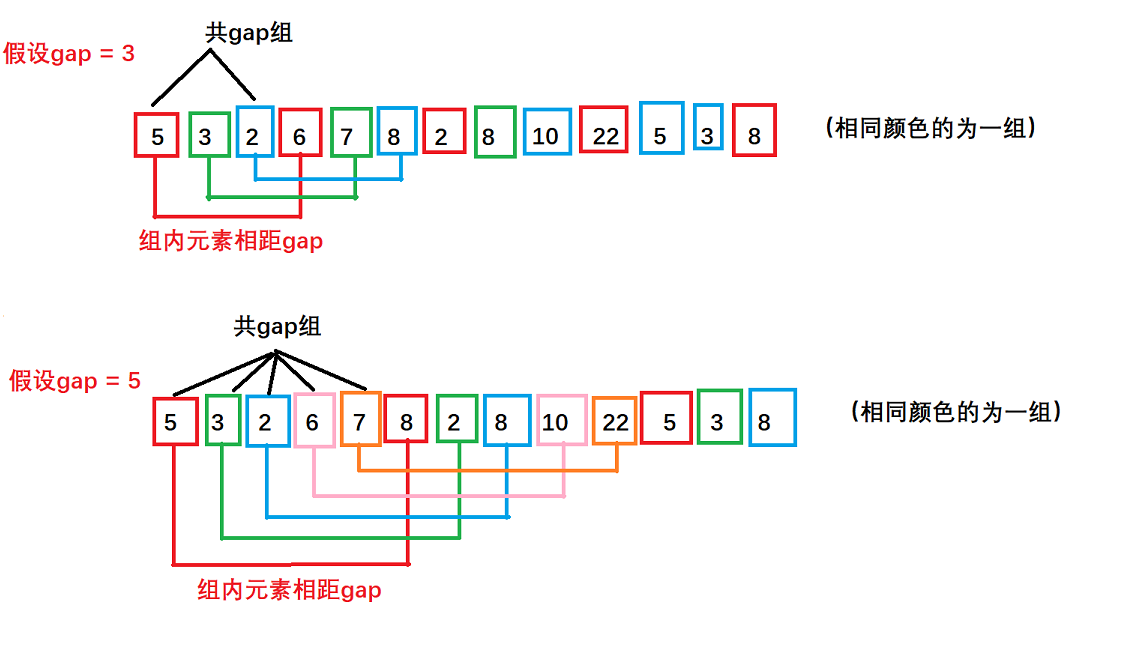

过程分析:
- 首先,我们需要对gap的初始值进行确定,这并没有一个确定的答案,一般是按照数据量来进行选取。一般我们选取gap = n/3 + 1或者gap = n/2作为gap的初始值。
- 根据算法的思想,我们观察到gap是在不断地进行缩小,最后缩小到1进行直接插入排序。因此我们gap的缩小增量可以继续使用gap = gap/3 + 1或gap = n/2来表示。
- 对1、2点进行合并后,我们可以这样用来表示gap的迭代更新:
int gap = n; //n为序列元素个数
while(gap > 1)
{//gap = gap/2;gap = gap/3 + 1;//每组进行直接插入排序//...
}
上面的循环在以下两种情况下会结束:
- n == 1:即
序列只有一个元素,此时无需进行排序,不会进入循环- n != 1 ,gap == 1:由于
gap的更新是在插入排序之前,因此当循环判断到gap == 1时,上一次进行的就是以1为gap增量的直接插入排序,此时序列已经有序,退出循环。
为什么要取gap = gap/3 + 1而不是gap = gap/3?
由于
最后gap要缩小到1进行直接插入排序,而如果我们选取gap = gap/3时,假设gap初始为6,第一次更新后gap=2,第二次更新后gap=0(向下取整),循环便结束了,并不会进行gap=1时的插入排序。因此,为了避免这种情况的发生,我们让gap = gap/3 + 1保证最后一次gap一定为1。
那为什么取gap = gap/2而不是gap = gap/2 + 1?
这种情况不需要处理的原因是
gap不可能等于0,因为进入循环的条件是gap>1,而gap只有等于0或1时gap/2才会为0。因此,无论gap初始为多少,最后一定都会在gap=1处停下。并且,当gap=2时,使用gap = gap/2 + 1会出现死循环/font>噢
- 每组之间进行的就是我们上面介绍的直接插入排序,不一样的是相邻元素的距离是gap而不是1。以下是gap = 3时的单趟希尔排序的动图过程:
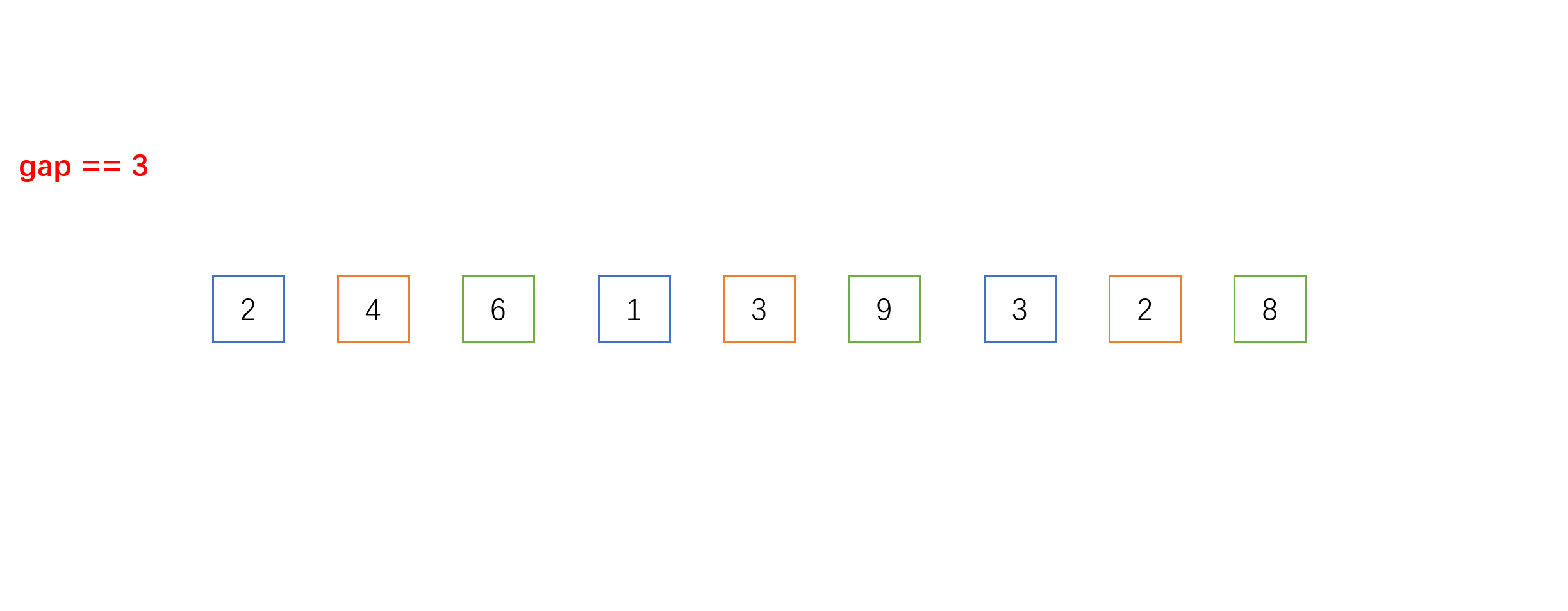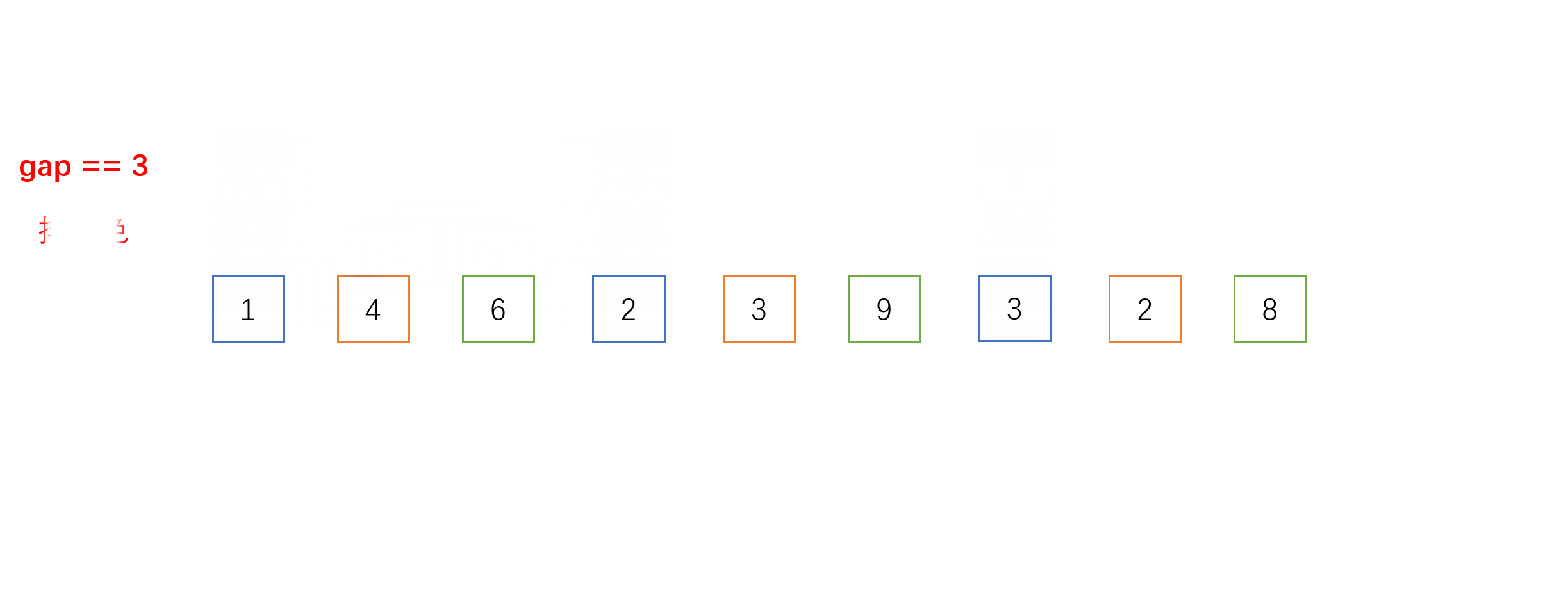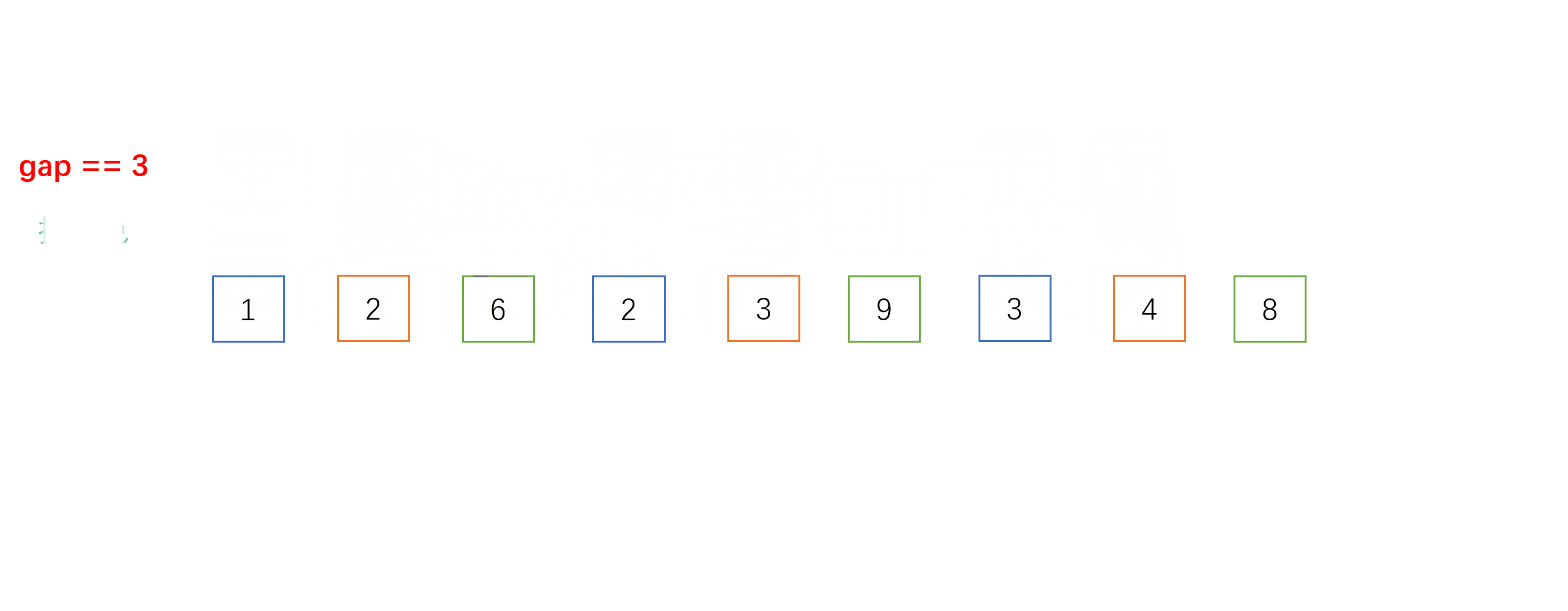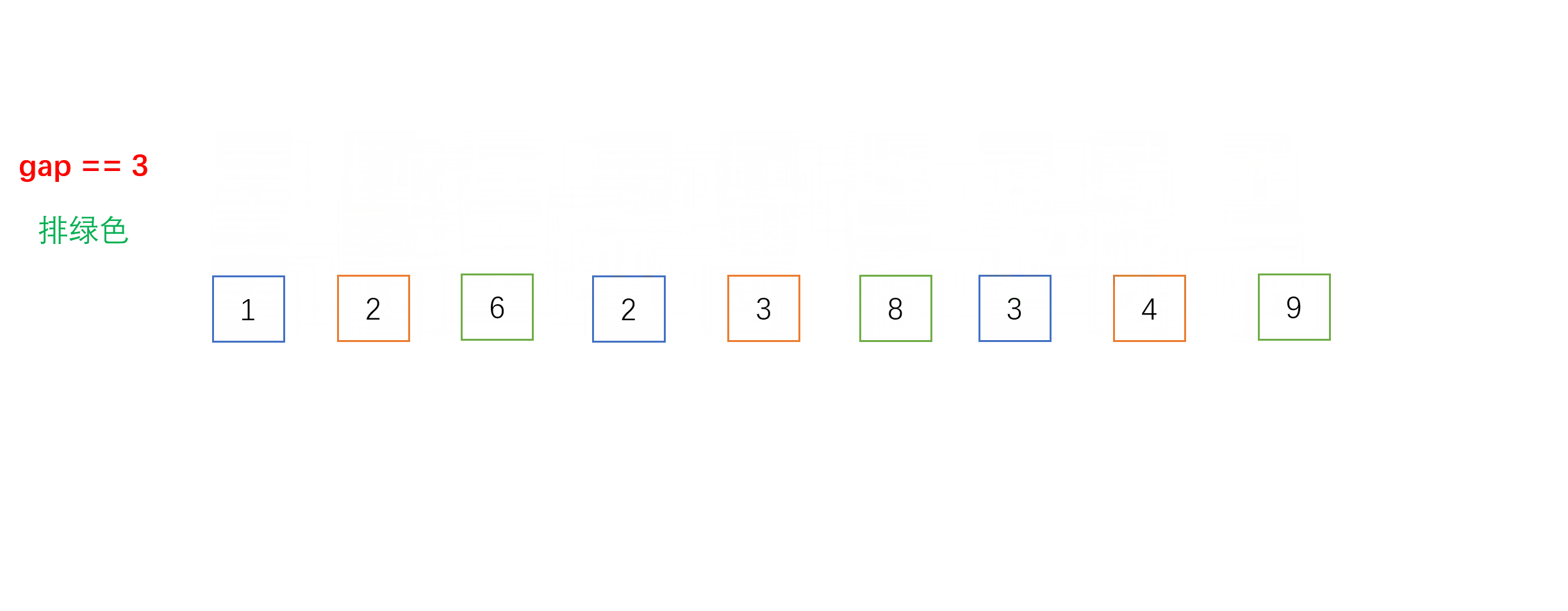
- 下面是希尔排序的全过程(以gap = gap/3 + 1为例):
- 通过观察,我们可以发现实际上
希尔排序就是直接插入排序的优化版。随着每一趟的分组排序,序列越来越接近有序。前面我们说过,直接插入排序在序列越接近有序的情况下效率越高,希尔排序就是通过每趟的预排序来使得序列越来越接近有序,从而提高直接插入排序的整体效率。 - 要点提炼:当gap > 1时,对序列进行分组预排序,目的是使得序列越来越接近有序;当gap == 1时,数组接近有序,此时进行直接插入排序效率大幅提高。
//写法1:一组一组排
void ShellSort1(int* a, int n)
{int gap = n;while (gap > 1){//1:gap > 1,预排序//2:gap == 1,直接插入排序gap = gap / 3 + 1; //缩小增量for (int j = 0; j < gap; j++) //一组一组进行插入排序,共gap组{//对当前组进行直接插入排序,组内相邻元素相距gap。//(其实就相当于把上面介绍的直接插入排序代码中的-1改成-gap即可)for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}
但是,上面的代码实际上还可以写得更加简洁
我们知道每个组的元素都相距gap,而组与组之间距离都为1。那么,我们实际上不用一组一组分开排,而是采用多组并排的方式,这样就可以少写一个for循环,代码如下
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
复杂度/稳定性分析
复杂度:
尽管上面的代码有多个循环嵌套,但这并不意味着希尔排序的效率低下。我们根据代码来分析一下希尔排序的时间复杂度,过程如下图所示:
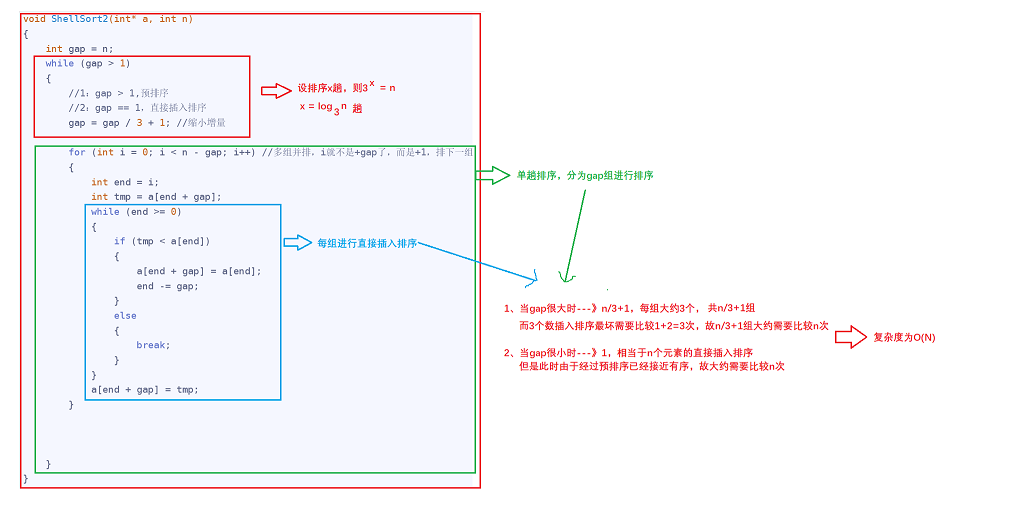
我们可以看到,在gap很大或者gap很小的情况下,每趟排序的时间复杂度为O(N),共进行log3n趟,那我们是不是可以认为希尔排序的时间复杂度为O(NlogN)?实际上并不行,因为当gap处于中间的过程时,时间复杂度的分析实际上是个很复杂的数学问题。每一趟预排序之后都对下一趟排序造成影响,这就好比叠buff的过程。
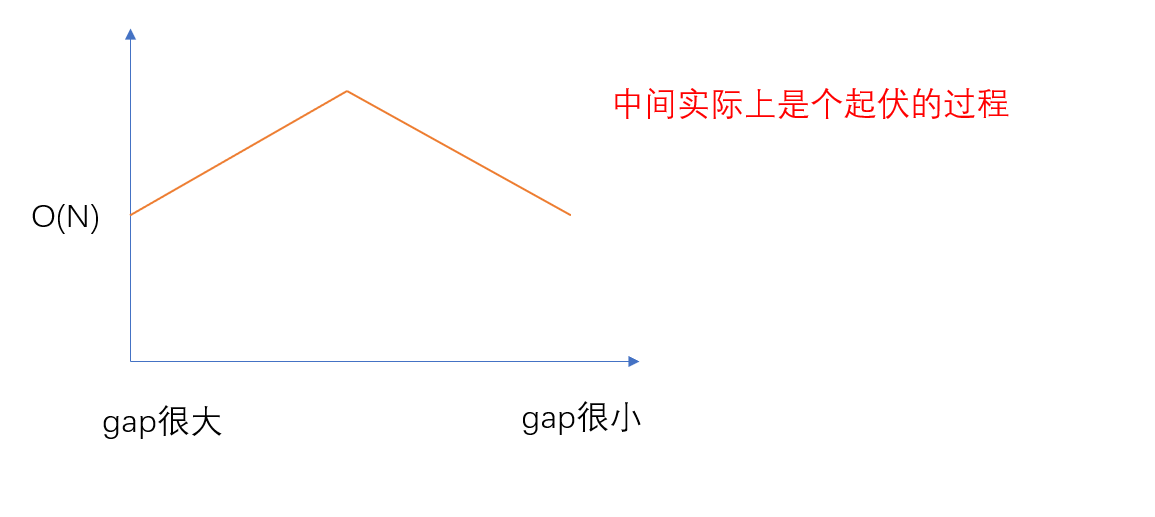
以下分别是两本书中对希尔排序时间复杂度的说法:
1、《数据结构(C语言版)》— 严蔚敏
2、《数据结构-用面相对象方法与C++描述》— 殷人昆
因为我们上面的gap是按照Knuth提出的方式取值的,并且Knuth进行了大量的试验统计,时间复杂度我们就按照:O(n^1.25)到O(1.6n^1.25)来进行取值。
然后就是空间复杂度,由于我们依旧只用到了常数级的辅助变量,因此空间复杂度为O(1)。
稳定性:
由于希尔排序是分组进行排序,当相同的数被分到不同组时,很可能就会改变相同的数的顺序,因此,希尔排序是不稳定的排序。

五、 选择排序
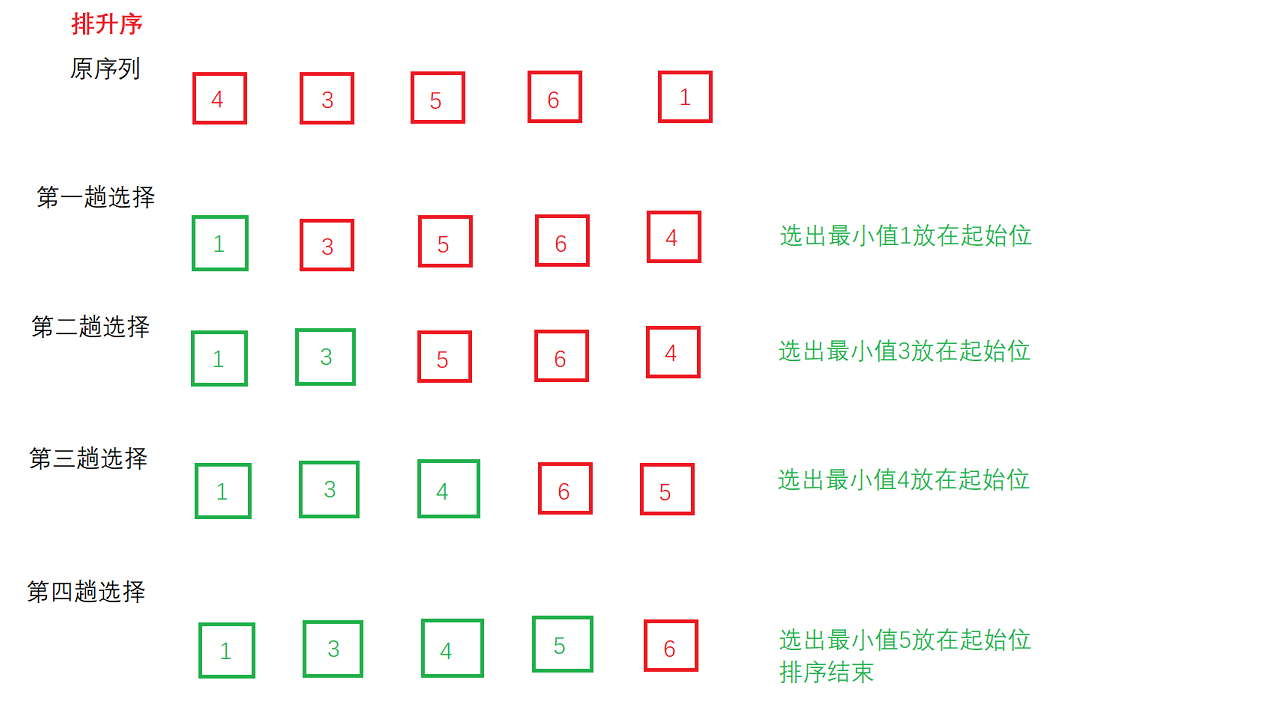
- 思想 : 每一次从待排序的数据元素中选出最小(升序)或最大(降序)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
- 选择过程:以下是对某个序列进行选择排序的过程:
- 动图演示:我们一样通过动图感受一下选择排序的过程:
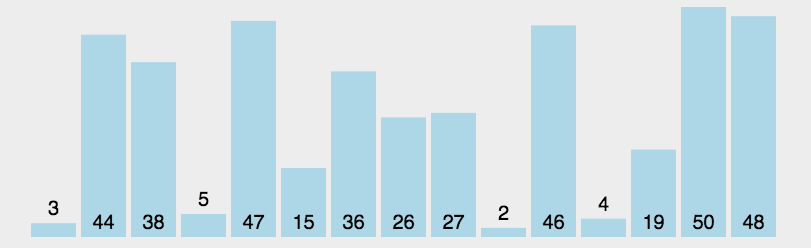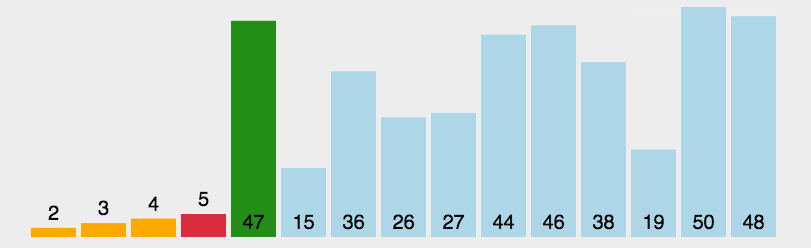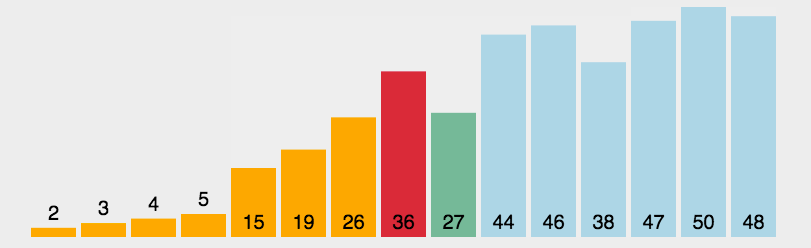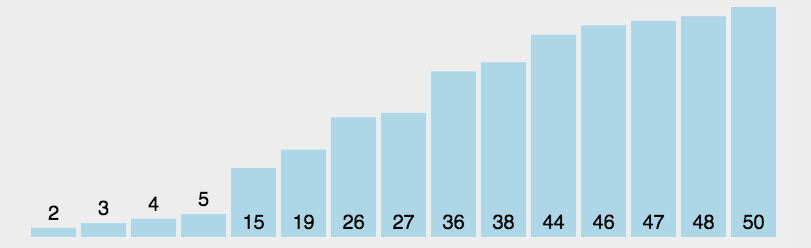
- 循环控制:类似的,我们需要两层循环来控制选择排序的过程。
内层循环遍历序列找出最大/最小值,外层循环控制选择的次数。 - 外层循环结束条件:每一次遍历完都可以选出一个数换到起始位置,一共N个数,故要选N-1次(最后一个数不需要选择)
for (int i = 0; i < n-1; i++) //外层循环,共要选择n-1次
{;
}
- 内层循环结束条件:内层循环通过比较进行选数,一开始N个数需要比较N-1次,然后每趟结束后下一次选择的起始位置就往后移动一位,比较次数减1
for (int i = 0; i < n-1; i++) //外层循环,共选择n-1次
{for (int j = i + 1; j < n; j++) //内层循环,起始位置开始向后进行比较,选最小值{;}
}
- 完整代码:
void swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void SelectSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) //外层循环,共选择n-1次{int mini = i; //记录最小值的下标,初始为第一个数下标for (int j = i + 1; j < n; j++) //内层循环,起始位置开始向后进行比较,选最小值{if (a[mini] > a[j]) //比最小值小,交换下标{mini = j;}}swap(&a[mini], &a[i]); //将最小值与起始位置的数据互换}
}
- 时间/空间复杂度:一共选了N-1次,每次选择需要比较N-1,N-2,N-3…次,加起来和冒泡一样时间复杂度为O(N);没有用到辅助空间,空间复杂度为O(1)
- 稳定性分析:由于是选数交换,在交换的过程中很可能会打乱相同元素的顺序,例如下面这个例子:
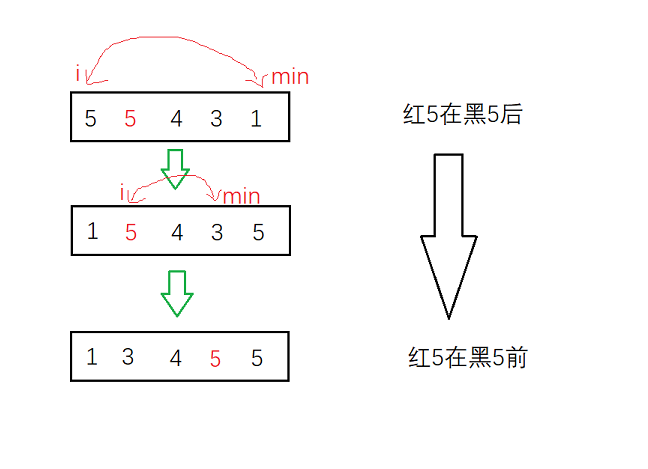
我们发现,在第一趟交换中,黑5被交换到了红5后面,在整个排序结束后,黑5依然在红5的后方,与最开始的顺序不一致。由此我们可以得出,选择排序是不稳定的排序。
六、各大排序算法的复杂度和稳定性
| 排序算法 | 时间复杂度(最好) | 时间复杂度(平均) | 时间复杂度(最坏) | 空间复杂度 | 稳定性 | 数据敏感度 |
|---|---|---|---|---|---|---|
| 冒泡排序 | 稳定 | 强 | ||||
| 选择排序 | 不稳定 | 弱 | ||||
| 直接插入排序 | 稳定 | 强 | ||||
| 希尔排序 | 不稳定 | 强 | ||||
| 堆排序 | 不稳定 | 弱 | ||||
| 快速排序 | 不稳定 | 强 | ||||
| 归并排序 | 稳定 | 弱 |
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位铁汁们的支持。文章有任何问题可以在评论区留言,小羊一定认真修改,写出更好的文章~~

相关文章:

【数据结构】手撕排序
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 一、排序的概念及其运用1.1 排序的概念1.2 常见的算法排序 二、 冒泡排序三、直接插入排…...

运维05:自动化
人工运维时代 运维人员早期需要维护众多的机器,因此需要执行很多重复的劳动,很多机器需要同时部署相同的服务或者是执行相同的命令,还得反复地登录不同的机器,执行重复的动作 自动化运维时代 早期运维人员会结合ssh免密登录&…...
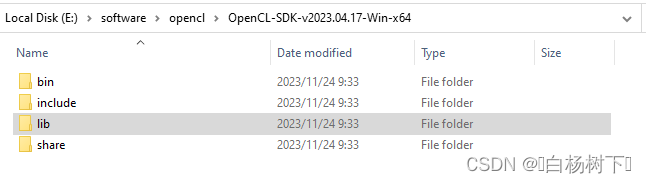
OpenCL学习笔记(一)开发环境搭建(win10+vs2019)
前言 异构编程开发,在高性能编程中有重要的,笔者本次只简单介绍下,如何搭建简单的开发环境,可以供有需要的小伙伴们开发测试使用 一、获取opencl的sdk库 1.使用cuda库 若本机有Nvidia的显卡,在安装cuda库后&#x…...

寻找两个正序数组的中位数
更好的阅读体验,请点击 YinKai s Blog。 题目:寻找两个正序数组的中位数 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 …...

探索低代码的潜力、挑战与未来展望
低代码开发作为一种新兴的开发方式,正在逐渐改变着传统的编程模式,低代码使得开发者无需编写大量的代码即可快速构建各种应用程序。然而,低代码也引发了一系列争议,有人称赞其为提升效率的利器,也有人担忧其可能带来的…...
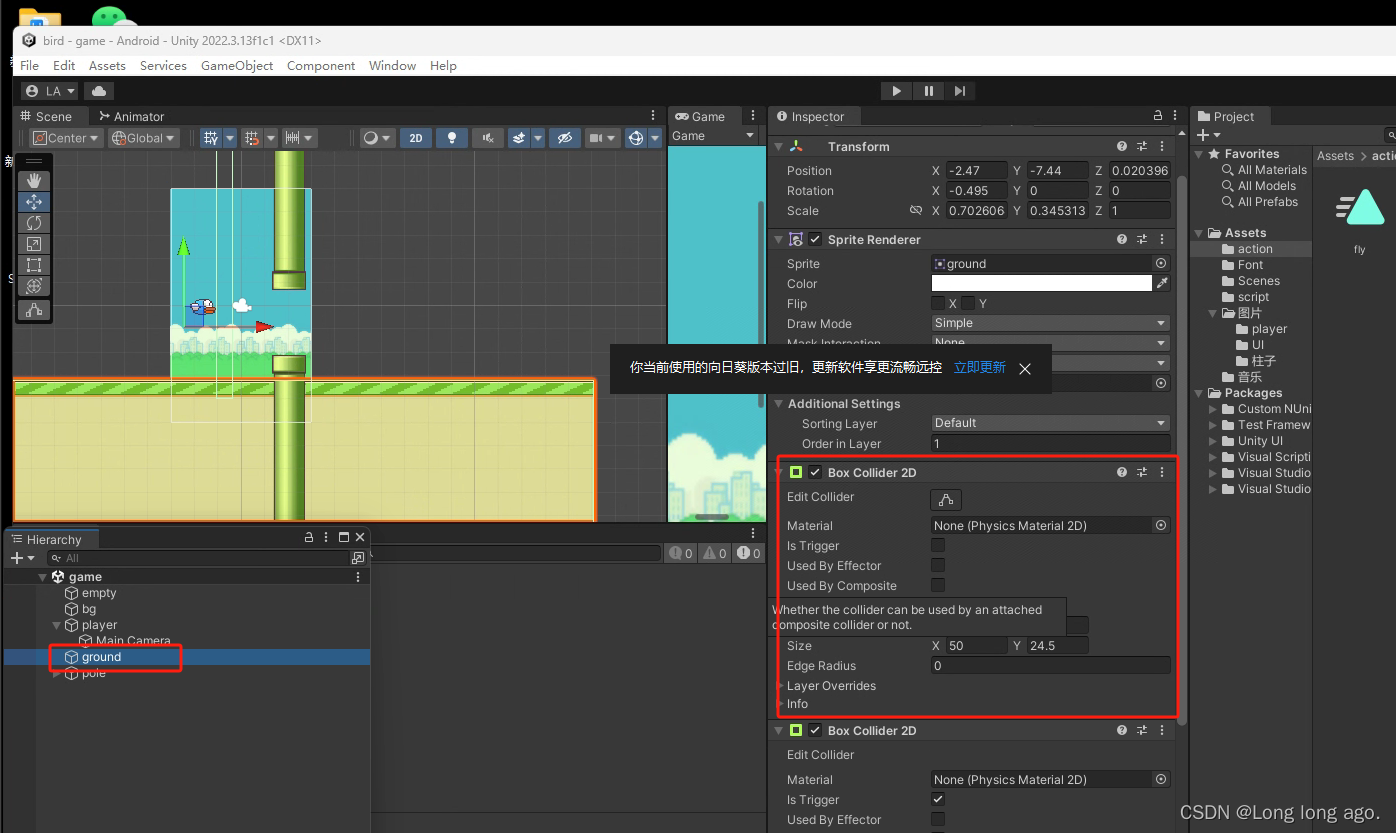
unity 2d 入门 飞翔小鸟 小鸟碰撞 及死亡(九)
1、给地面,柱体这种添加2d盒装碰撞器,小鸟移动碰到就不会动了 2、修改小鸟的脚本(脚本命名不规范,不要在意) using System.Collections; using System.Collections.Generic; using UnityEngine;public class Fly : Mo…...
工具)
实时最优控制(Real-Time Optimal Control)工具
系列文章目录 前言 许多现代控制方法,如模型预测控制(model-predictive control),在很大程度上依赖于实时解决优化问题。特别是,高效解决优化控制问题的能力使复杂机器人系统在实现高动态行为(highly dyna…...
(env: Windows,mp,1.06.2308310; lib: 3.2.4) uniapp微信小程序
应公司需求,在特定情况下需要修改ip 在开发过程中出现的小插曲 1、第一种情况:重复声明 2、第二种情况: 应官方要求,需要跳转的 tabBar 页面的路径(需在 pages.json 的 tabBar 字段定义的页面)࿰…...

go-zero开发入门-API服务开发示例
接口定义 定义 API 接口文件 接口文件 add.api 的内容如下: syntax "v1"info (title: "API 接口文件示例"desc: "演示如何编写 API 接口文件"author: "一见"date: "2023年12月07日"version: "…...

NVIDIA Jetson NX ubuntu20.04删除多余版本冲突的Boost库
参考Ubuntu16.04 卸载旧版本Boost库并安装新版本 卸载 删除/usr/local/include/boost文件夹,删除/usr/local/lib中和boost有关的文件,以及/usr/local/lib/cmake/中boost的cmake文件 cd /usr/local/lib/ ls | grep boost sudo rm -rf /usr/local/include/boost su…...

【蜗牛到家】获南明电子信息产业引导基金战略投资
智慧社区生活服务平台「蜗牛到家」已于近期获得贵阳南明电子信息产业引导基金、华科明德战略投资。 贵阳南明电子信息产业引导基金属于政府旗下产业引导基金,贵州华科明德基金管理有限公司擅长电子信息产业、高科技产业、城市建设及民生保障领域的投资,双…...

基于ubuntu nc指令实现远程传输文件到嵌入式设备中
背景: 最近在使用nc进行远程文件传输的时候发现在文件传输完成时,没有正确的反馈,而是界面一直停留在传输阶段,加上使用nc传输需要设置一些诸如-l、 -p等参数,于是想将这些参数包裹在sh脚本中,一键执行脚本…...

蓝桥杯 day01 奇怪的数列 特殊日期
奇怪的数列 题目描述 奇怪的数列 从 X 星截获一份电码,是一些数字,如下: 13 1113 3113 132113 1113122113 ⋯⋯ YY 博士经彻夜研究,发现了规律: 第一行的数字随便是什么,以后每一行都是对上一行…...

properties配置和读取
如何配置和读取属性文件 1.属性文件介绍1.1 什么是属性文件1.2属性文件规范1.3 属性文件优缺点 2.属性文件读取4.spring和属性文件4.1利用注解读取4.2配置文件里直接引用 4.属性文件写入5.注意事项5.总结 1.属性文件介绍 1.1 什么是属性文件 Java开发中,我们经常需…...
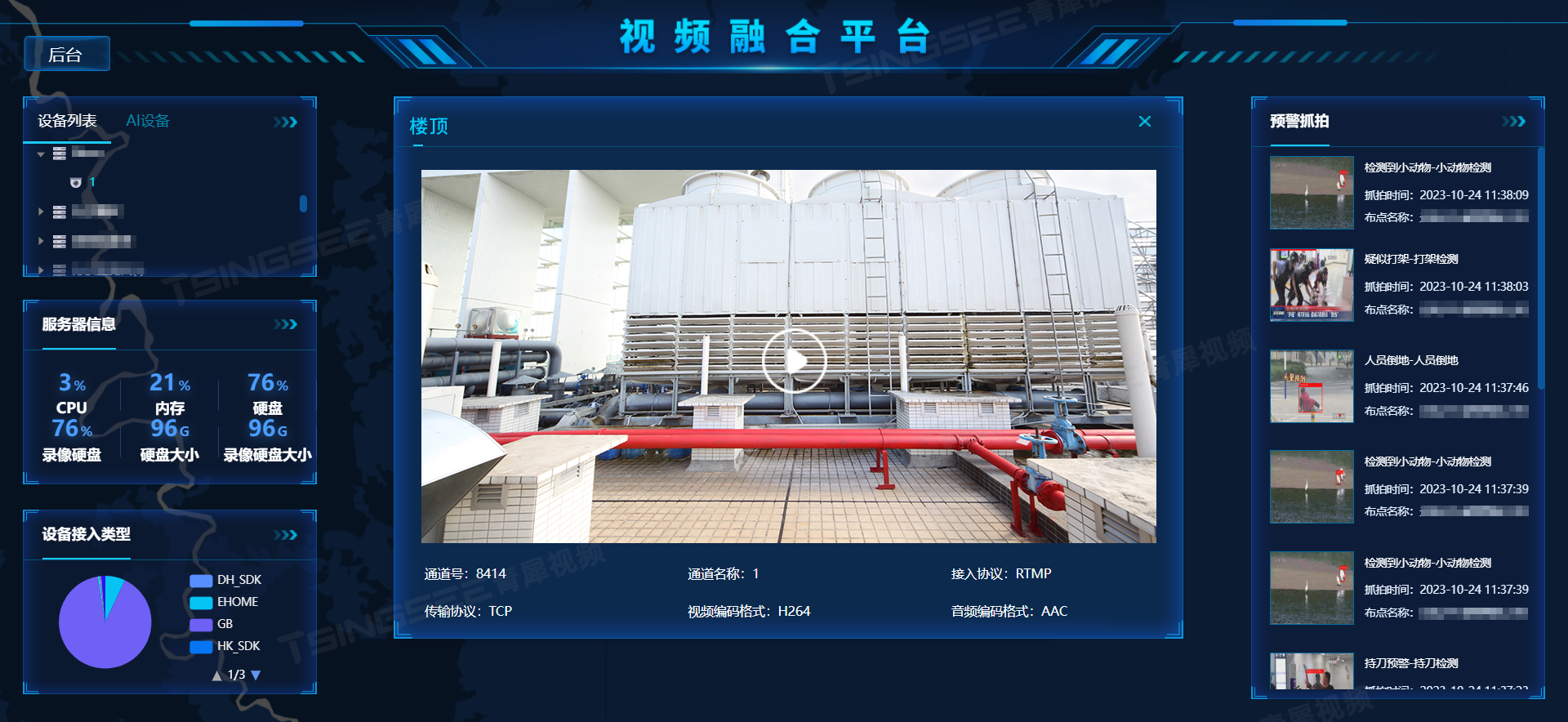
如何利用人工智能+物联网技术实现自动化设备生产
随着科技的发展与行业竞争的日益激烈,制造业也逐渐走向智能化发展。制造业的改革是利用物联网技术和自动化设备,实现生产线的智能化和自适应生产,优化生产流程,提高生产效率和质量,为企业创造更大的价值。 方案概述 智…...
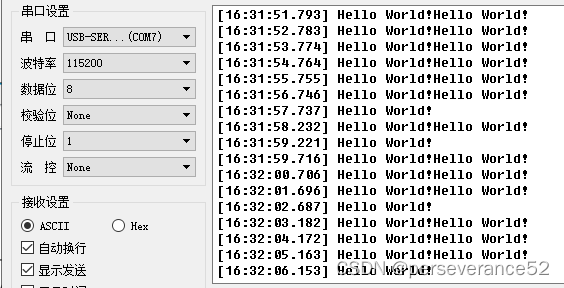
STM32CubeMx+MATLAB Simulink串口输出实验
STM32CubeMxMATLAB Simulink串口输出实验 📌《STM32CubeMxMATLAB Simulink点灯程序》📍相关篇《MATLAB Simulink STM32硬件在环 (HIL)实现例程测试》🔖需要的软件支持包:Embedded Coder Support Package fo…...

React中每次渲染都会传入一个新的props.children到子组件?
传入props.children后, 为什么会导致组件的重新渲染? 问题描述 在 react 中, 我想要对组件的渲染进行优化, 遇到了一个非常意思的问题, 当我向一个组件中传入了 props.children 之后, 每次父组件重新渲染都会导致这个组件的重新渲染; 它看起来的表现就像是被memo包…...

Qt 通过命令行编译程序
前言 从服务器拉代码到编译成可执行文件一个脚本解决问题。使用的项目文件见上一个文章 Qt生成动态链接库并使用动态链接库 脚本代码 为了方便易懂这是一个很简单的Qt编译脚本 call E:\vs2015\VC\vcvarsall.bat x86 rmdir /s /q my-project git clone gitgitee.com:wenbai1…...
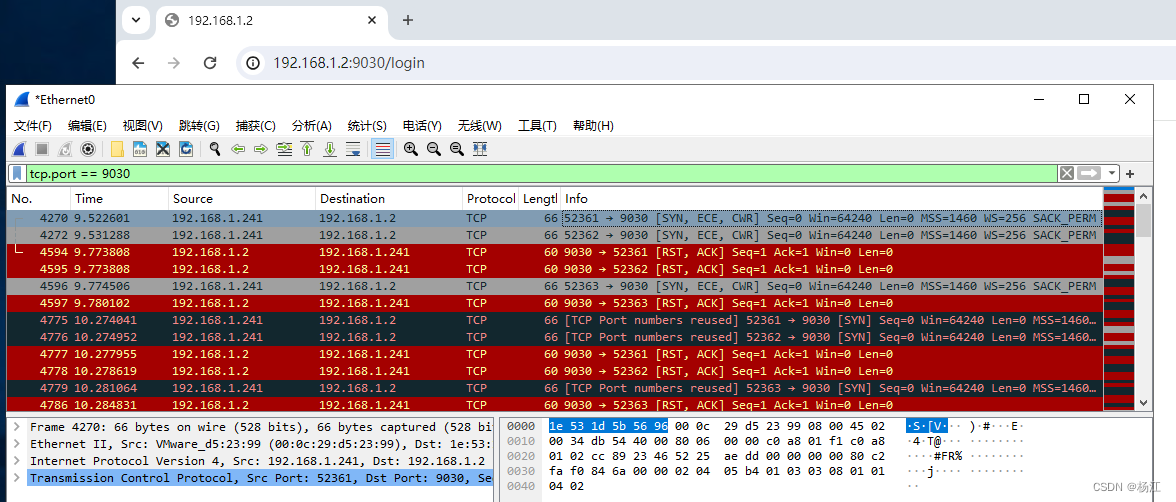
WireShark监控浏览器登录过程网络请求
软件开发中经常前后端扯皮。一种是用Chrome浏览器的开发者工具 来看网络交互,但是前提是 网络端口的确是通的。 WireShark工作在更低层。 这个工具最大的好处,大家别扯皮,看网络底层的log,到底 你的端口开没开, 数据…...
202301209将RK3399的挖掘机开发板在Android10下设置系统默认为24小时制
202301209将RK3399的挖掘机开发板在Android10下设置系统默认为24小时制 2023/12/9 22:07 应该也可以适用于RK3399的Android12系统 --- a/frameworks/base/packages/SettingsProvider/res/values/defaults.xml b/frameworks/base/packages/SettingsProvider/res/values/default…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...


